|
|
| 第2,475行: |
第2,475行: |
|
| |
|
| 结果表明,Y染色体与细胞器基因座的<math display="inline">F_{S T}</math>预期更高(因其有效种群更小,见图4.15)。当所有类型基因座共享相同迁移率时,相较于二倍体核基因座,Y染色体与线粒体基因座的<math display="inline">\boldsymbol{F}_{S T}</math>水平高四倍。亚种群间Y染色体与细胞器基因座的分化程度更高,完全源于这些基因座自交合特性的差异导致遗传漂变引起的固定或丢失速率增加。详见Hu与Ennos(1999)及Hamilton与Miller(2002)。 | | 结果表明,Y染色体与细胞器基因座的<math display="inline">F_{S T}</math>预期更高(因其有效种群更小,见图4.15)。当所有类型基因座共享相同迁移率时,相较于二倍体核基因座,Y染色体与线粒体基因座的<math display="inline">\boldsymbol{F}_{S T}</math>水平高四倍。亚种群间Y染色体与细胞器基因座的分化程度更高,完全源于这些基因座自交合特性的差异导致遗传漂变引起的固定或丢失速率增加。详见Hu与Ennos(1999)及Hamilton与Miller(2002)。 |
|
| |
| = 第5章 =
| |
|
| |
| === 突变 ===
| |
|
| |
| <span id="所有遗传变异的来源"></span>
| |
| ==== 5.1 所有遗传变异的来源 ====
| |
|
| |
| 突变类型与突变率。低概率的突变事件如何解释遗传变异?突变的适应度谱。突变率的估算。突变率的演化。
| |
|
| |
| 前面的章节详细讨论了随机和非随机交配下的基因型频率、遗传漂变与有效种群大小的关系,以及种群分化和基因流。这些过程与种群中所有其他机制共同作用,塑造或改变种群现有的遗传变异。但遗传变异最初从何而来?Hardy-Weinberg定律明确显示,颗粒遗传本身不会改变基因型或等位基因频率,因此并非遗传变异的来源。任何形式的非随机交配仅改变基因型频率而保持等位基因频率不变。遗传漂变通过抽样误差导致等位基因频率变化并最终走向固定或丢失,从而侵蚀遗传变异。基因流仅通过分配亚种群间的遗传变异来改变种群结构模式。'''突变'''——脱氧核糖核酸(DNA)中随机错误的永久性整合,导致祖先与后代DNA序列拷贝间的差异——是一切遗传变异的终极来源。
| |
|
| |
| 本章将涵盖突变过程,首先描述突变的模式与速率。后续章节将介绍经典群体遗传模型中关于新突变命运、突变对种群等位基因频率的影响,以及遗传漂变清除遗传变异与突变补充变异之间的预测平衡。本章还将讨论群体遗传学中常用的几种新等位基因引入模型,并通过案例阐明这些模型的后果。最后部分将展示如何将突变过程整合到谱系分支模型中。
| |
|
| |
| '''突变'''是一个广义术语,涵盖导致DNA序列改变的多种事件。'''点突变'''指单个碱基对被另一核苷酸替换。化学性质相似的核苷酸间(嘌呤间<math display="inline">\mathrm{(A{\leftrightarrow}G)}</math>或嘧啶间<math display="inline">\mathrm{(C{\leftrightarrow}T)}</math>)的点突变称为'''转换''',而化学性质相异核苷酸间(嘌呤与嘧啶互变)的点突变称为'''颠换'''。编码基因内的碱基替换可能改变或不改变该基因编码的蛋白质:'''同义突变'''(沉默突变)因遗传密码的简并性保持DNA序列翻译产物不变,'''非同义突变'''(错义突变)则导致密码子改变从而影响氨基酸序列。
| |
|
| |
| 突变可以表现为DNA序列的插入或缺失(常简称为''indels'')。若编码区内的''indels''导致序列长度变化不是三的整数倍,则会引发移码突变,从而改变DNA序列的翻译过程,并可能产生提前终止密码子。''Indels''的规模可从一个碱基对到包含数千碱基对的染色体区段不等。
| |
|
| |
| 同源基因多次复制形成的多拷贝阵列称为多基因家族,这类结构由重复事件产生。此类重复基因的某些拷贝可能因突变积累而丧失功能,成为假基因(''pseudogene'')。基因转换(''gene conversion'')可能导致多基因家族中多个位点的序列同质化。基因转换的发生源于减数分裂过程中不恰当的错配修复。当两条同源染色体在DNA复制期间处于单链状态时,其部分区域可能发生退火。若这些区域的序列存在细微差异,退火区段将包含单核苷酸错配。这些错配随后会被通常参与DNA复制校对(''proofreading'')的酶修复为正确的沃森-克里克(Watson–Crick)碱基配对。当同一基因被多次重复时,姐妹染色体间的退火过程往往频繁发生,这是因为基因拷贝的序列高度相似,染色体可在基因阵列的任何位置退火。其结果是,多基因区域内的所有基因拷贝倾向于在不发生重组的情况下收敛于某一随机版本的DNA序列。
| |
|
| |
| 突变还可表现为染色体重排:染色体区域形成环状结构,导致某区段断裂并以反向取向修复,称为倒位(''inversion'')。易位(''translocation'')突变指染色体片段从一条染色体脱离后,通过修复机制整合到非同源染色体中。转座元件(''transposable elements'')——能够在基因组内移动并自我复制的DNA片段——是易位突变的常见诱因。侧向或水平基因转移(''lateral/horizontal gene transfer''),即DNA片段在不同个体甚至物种间的移动与整合,是原核生物中相对频繁发生的另一类突变途径。关于这些突变类型分子机制的更多细节,请参阅Krebs等(2017)的著作。
| |
|
| |
| 位点或碱基对发生突变的概率是群体遗传学中的关键参数,因为突变速率决定了新遗传变异加入群体的速度。尽管看似矛盾,但精确估计多种生物类型的突变速率实际上相当困难(参见Drake等1998;Fua和Huai 2003;Lynch等2016)。
| |
|
| |
| 考虑一个单一报告基因座(reporter locus)的突变率案例,该基因座对生物体表型(如小鼠被毛颜色)的影响已被充分理解。用于估计突变率的数据是子代中与被毛颜色基因型已知的父母预期不符的被毛颜色个体数。将具有意外被毛颜色的子代数量除以检测的总子代数量看似简单。然而,这种计算估计的是由被毛颜色基因座分子变化引起的可检测表型改变的频率。这是对该基因座所有类型突变发生频率的估计,而非突变率的估计。
| |
|
| |
| 这种突变频率的估计可能也不完整,因为仅包含导致被毛颜色显著变化的突变。并非所有突变都会反映在被毛颜色上,例如密码子第三位核苷酸的沉默(synonymous)变化不会改变基因的最终氨基酸序列。此外,突变对被毛颜色的影响可能不同,某些突变对表型的影响可能微弱或难以观察。因此,表型可观察变化的频率并不等同于突变率。
| |
|
| |
| 突变率的估计需要更多信息。一个关键细节是基因座或基因组经历的复制次数,因为突变通常发生在复制过程中。不同细胞类型和物种在生长与繁殖过程中经历的细胞复制次数不同。例如,哺乳动物雄性配子的突变频率高于雌性配子,这是因为精子形成前经历的细胞分裂次数远多于卵子。然而,雄性和雌性配子的基础突变率可能相同,差异仅源于基因组复制次数的不同。
| |
|
| |
| 另一组需要考虑的因素是可突变基因座或基因组的大小。以假设的小鼠被毛颜色基因为例,该基因座的碱基对数量是关键信息。若基因座有900或90个碱基对,则基于被毛颜色变化频率估计的每碱基对突变率将大不相同。
| |
|
| |
| 突变频率与突变率的区别突显了一个事实:群体遗传学中的突变率会根据实验方法和生物体生命周期以不同形式表达。突变目标可以是整个基因组、一个基因座或单个碱基对,而速率可以表示为每次DNA复制或每个有性世代的时间单位。只有当目标大小和时间单位表达一致时,突变率的比较才有意义。通常,涉及有性真核生物的群体遗传预测中,每个有性世代的突变率是相关单位。而对原核生物(如''Escherichia coli''或酵母)的预测则更自然地使用每次细胞分裂的突变率。
| |
|
| |
| 表 5.1 近交系小鼠毛色表型相关五个基因座的单位点突变率(Schlager 和 Dickie 1971)。显性突变通过检测兄妹交配产生的F1代毛色进行计数。隐性突变需检测隐性等位基因纯合近交系与显性”野生型”等位基因纯合系杂交产生的F1代毛色。这些估算数据的工作量极为惊人,涉及约700万只小鼠长达6年的观测。
| |
|
| |
| {|
| |
| !width="14%"| Locus
| |
| !width="17%"| Gametes tested
| |
| !width="22%"| Mutations observed
| |
| !width="45%"| Mutation rate per locus x10^-6 (95% Cl)
| |
| |-
| |
| | '''Mutations from dominant to recessive alleles'''
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | ''Albino''
| |
| | 150391
| |
| | 5
| |
| | 33.2 (10.8 - 77.6)
| |
| |-
| |
| | ''Brown''
| |
| | 919699
| |
| | 3
| |
| | 3.3 (0.7 - 9.5)
| |
| |-
| |
| | ''Dilute''
| |
| | 839447
| |
| | 10
| |
| | 11.9 (5.2 - 21.9)
| |
| |-
| |
| | ''Leaden''
| |
| | 243444
| |
| | 4
| |
| | 16.4 (4.5 - 42.1)
| |
| |-
| |
| | ''Non-agouti''
| |
| | 67395
| |
| | 3
| |
| | 44.5 (9.2 - 130.1)
| |
| |-
| |
| | All loci
| |
| | 2220376
| |
| | 25
| |
| | 11.2 (7.3 - 16.6)
| |
| |-
| |
| | '''Mutations from recessive to dominant alleles'''
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | ''Albino''
| |
| | 3423724
| |
| | 0
| |
| | 0 (0.0 - 1.1)
| |
| |-
| |
| | ''Brown''
| |
| | 3092806
| |
| | 0
| |
| | 0 (0.0 - 1.2)
| |
| |-
| |
| | ''Dilute''
| |
| | 2307692
| |
| | 9
| |
| | 3.9 (1.8 - 11.1)
| |
| |-
| |
| | ''Leaden''
| |
| | 266122
| |
| | 0
| |
| | 0 (0.0 -13.9)
| |
| |-
| |
| | ''Non-agouti''
| |
| | 8167854
| |
| | 34
| |
| | 4.2 (2.9 - 5.8)
| |
| |-
| |
| | All loci
| |
| | 17236978
| |
| | 43
| |
| | 2.5 (1.8 - 3.4)
| |
| |}
| |
|
| |
| 突变最普遍的规律是:它是发生概率极低的稀有事件。在一项涉及数百万只小鼠的经典实验中,通过五个对毛色表型有显著影响的基因估算了突变率(表5.1;Schlager和Dickie 1971)。每个基因的突变率在每百万配子中1.8到16.6次突变之间,相当于每世代每个基因座<math display="inline">\left(1.8–16.6\right)\times{10}^{-6}</math>的突变率。近期辐射研究也报道了小鼠极为相似的突变率(Russell和Russell 1996)。野生型向新等位基因的突变率(称为正向突变)比新等位基因向野生型的突变率(称为回复突变)高出近一个数量级。这种基因座正反向突变率的不对称性是突变实验中的常见现象,其本质原因是:相较于功能受损后精确恢复原有功能的途径,导致正常等位基因功能异常的突变途径更多样。在此意义上,正反向突变率的概念仅适用于通过表型效应检测突变的情形。【“forward mutations”译为“正向突变”】【“reverse mutations”译为“回复突变”】
| |
|
| |
| 像突变这样的低概率事件如何能为种群增加不止微量的遗传变异?让我们以人类为例,通过计算初步回答这个问题。综合基因组编码区和非编码区的平均,人类核基因组的近似突变率约为每代每碱基对(bp)<math display="inline">\mathrm{1}\times\mathrm{10}^{-9}</math>次突变。单倍体基因组(一个精子或卵子)包含约<math display="inline">3.2\times10^{9}</math>碱基对(bp)。每个二倍体个体的每个基因组将具有:
| |
|
| |
| <math display="block">
| |
| \begin{array}{r}{\left(1\times10^{-9}\mathrm{mutations\ bp}^{-1}\mathrm{generation}^{-1}\right)}\ {\left(2\times3.2\times10^{9}\mathrm{bp}^{-1}\right)=6.4\mathrm{mutations}}\end{array}
| |
| </math>
| |
|
| |
| 其中系数2来源于二倍体基因组。我们每个人与父母中一方的基因组差异约为该数值的一半,即平均约3个突变。如果所有突变都是随机事件且在基因组中均匀分布,则每对个体间的差异约为该突变数的两倍,即平均约13个突变差异。
| |
|
| |
| 突变对可用遗传变异的整体影响取决于种群规模。2019年中期全球人口约为75.71亿(参见http://www.census.gov/popclock)。基于这一人口规模,预计人群中总共有:
| |
|
| |
| 或超过480亿个单核苷酸突变存在于人类种群中。这意味着每代突变的绝对数量可能非常高,其数量取决于突变率、种群规模和基因组大小。我们将在本章后续重新讨论这一主题,以更正式地预测当突变输入的遗传变异与遗传漂变导致的遗传变异损失达到平衡时的预期杂合度水平。
| |
|
| |
| 突变等位型(作为杂合或纯合基因型的一部分)对个体表型的影響可能差异极大。由于自然选择与遗传漂变是决定新突变命运的关键过程,表型最常被置于其生存率、繁殖率或适应度(fitness)的框架下考量。个体突变等位型的可能适应度范围可被视作一种突变适应度谱(mutation fitness spectrum),如图5.1所示。所有突变对表型产生的适应度效应均相对于种群的平均适应度(关于适应度与平均适应度的定义详见第6章)。有害突变(detrimental or deleterious mutations)会降低生存与繁殖能力,而能提升生存与繁殖能力的突变则为有利突变。极端有害的突变(如导致死亡的致死突变(lethals)或无法产生可存活后代的情况)会受到自然选择的强烈抑制,通常无法延续超过一代。具有强烈有害性且接近致死程度的突变有时被称为亚致死突变(sublethals)。对适应度有微弱正向或负向影响的突变(图5.1中平均适应度周围的阴影区域)被称为中性或近中性突变,因为它们的命运将完全或主要由遗传漂变的抽样误差所决定。最后一类是有利突变(beneficial mutations),其能提升生存与繁殖能力至高于种群平均适应度的水平。需特别指出的是,突变的适应度效应可能高度依赖环境背景(见Fry and Heinsohn 2002)及其他位点的基因型。本章后续模型将探讨这些不同类型的突变,展示适应度如何影响新突变在种群中丢失或达到固定(fixation)的概率。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/e7d8283cb35b8d4886cabc31a6cddaea48ef7ea0dc03114986e6b056cf3f97b6.jpg]]<br />
| |
| '''图5.1''' 突变对表型影响的假设性分布,这些影响最终作用于基因型的达尔文适应度。平均适应度低于种群平均适应度<math display="inline">(\overline{{\boldsymbol{\mathsf{W}}}})</math>的突变会因自然选择而频率下降。<math display="inline">\overline{{\boldsymbol{W}}}</math>周围的阴影区域表示突变对适应度的影响相对于遗传漂变效应较小的区间(中性区的宽度取决于有效种群大小)。接近零平均适应度的阴影区域表示导致繁殖失败或致死的突变。致死突变更为常见,因为该类别包含由多种原因导致的不同严重程度的突变。由于突变事件的稀有性、多数突变的微弱效应以及适应度对环境背景的依赖性,突变适应度效应本质上难以测量。
| |
|
| |
| '''突变适应度谱(Mutation fitness spectrum)''':新突变平均适应度的频率分布,以参考种群的平均适应度为基准进行测量。<br />
| |
| '''漂变屏障假说(Drift barrier hypothesis)''':该假说预测突变率将通过自然选择向下演化,直至自然选择的响应受限于遗传漂变。其核心预测是突变率与<math display="inline">N_{e}</math>呈负相关。
| |
|
| |
| 突变适应度谱在解释种群遗传学和进化中众多现象的广泛假说中占据核心地位(参见Charlesworth和Charlesworth 1998;Orr 2003;Estes等 2004;Agrawal和Whitlock 2012;Lynch等 2016)。对于近交衰退、交配系统进化、性与重组的进化以及适应速率等普遍而多样的现象的解释,部分依赖于突变适应度谱的本质特性。强烈有害或强烈有利的突变将分别被自然选择稳定且可预测地驱向丢失或固定。然而,对适应度影响较小的突变(相对于有效种群大小而言)的固定或丢失,完全或部分归因于随机遗传漂变。其结果是,轻度有害突变可能通过偶然性达到固定并随时间在种群中积累。类似地,某些轻度有利突变也可能因偶然性从种群中丢失。轻度有害突变的积累会降低个体适应度,并可能增加灭绝风险,从而导致自然选择作用于那些减少种群中有害突变负荷的过程。有利突变的频率也可能通过正向自然选择限制进化速率。因此,图5.1中示意显示的频率分布的具体形态,既提供了关于单个突变命运的關鍵信息,也揭示了种群中持续突变的长期后果。
| |
|
| |
| ==== 估计突变速率 ====
| |
|
| |
| 估计一个物种内的突变速率主要有三种方法。第一种方法由Luria和Delbruc(1943)在其经典实验中所提出,该实验旨在验证关于突变何时为种群贡献遗传变异的两种可能解释——突变是随机持续发生的,还是因胁迫或刺激而产生的(后者有时被称为定向突变【“directed mutation”译为”定向突变”】)。Luria和Delbruc使用少量细胞起始培养易受噬菌体感染的''E. coli''液体培养物。他们同时制备了在表面铺有培养的噬菌体的琼脂平板,并将细菌涂布于平板上。由于噬菌体会感染并裂解细菌,平板上仅会出现少数携带赋予抗性突变的细菌菌落。Luria和Delbruc预测,若抗性突变是随机发生的,则突变数量将符合均值与方差相等的泊松分布。观测到的噬菌体抗性菌落数符合泊松分布,从而否定了定向突变假说。(Meneely(2016)对Luria和Delbruc实验及其基于泊松分布的预期进行了深入阐述。)这种波动试验通过平行培养的多个重复系中观察到的突变数方差进行估算,同时基于泊松分布估计平均突变数(Sarkar et al. 1992)。将平均突变数除以细胞分裂次数和碱基对数量即可估算突变速率。波动试验目前仍被使用,因其可与全基因组测序结合来估算每碱基对的突变速率(例如Gou et al. 2019)。
| |
|
| |
| 另一种广泛使用的突变速率估计方法及突变适应度谱【“mutation fitness spectrum”译为”突变适应度谱”】形态分析方法,是通过建立一系列遗传相同的种群,使其中部分种群经历多代突变积累,同时维持一个不经历突变的对照种群。随后在不同时间点将突变种群的生存力与繁殖表型与对照种群进行比较,以估计突变引起的平均适应度变化。这种比较被称为突变积累实验,因为在独立重复种群中,突变会通过多代的遗传漂变被反复固定(Halligan和Keightley 2009)。
| |
|
| |
| 如果完全没有突变,突变积累实验中的复制种群将随时间推移始终保持相同的存活率,因为每个种群最初在遗传上是完全相同的。然而,突变会随机发生,并在不同种群中引起独立的遗传变化,导致种群间存活率的分化。假设突变适应度谱围绕平均适应度对称分布,使得相同幅度的有害突变和有益突变频率相等。这种情况下,由于大量突变样本中同等大小的有益突变和有害突变会相互抵消,突变积累实验中各品系的平均存活率不会发生变化。然而,存活率的方差将会增加,因为随着突变数量的积累,种群间存活率的分布范围会不断扩大。
| |
|
| |
| 接下来,假设存在如图5.1所示的突变适应度谱,其中有害突变比有益突变更常见。随着突变的积累,由于有害突变更普遍,各品系的平均存活率应当下降。突变分布越偏向有害突变,复制种群的平均存活率下降速度就越快。
| |
|
| |
| 若干经典的突变积累研究结果对人们对突变适应度谱的认知产生了重大影响,这些研究估测了影响黑腹果蝇(''Drosophila melanogaster'')生存力的突变频率分布(Mukai 1964; Mukai et al. 1972)。果蝇的突变积累实验依赖于特殊的育种设计——通过多代维持多个重复纯合家系或品系中不经历重组的第二染色体。所有类型的突变均发生在这条非重组染色体上,并通过每代单雄建系导致的遗传漂变在各品系中被固定。每隔10代,所有独立品系的果蝇均会与未经历染色体倒位引发突变的对照组进行生存力比较【“assayed”译为“测定”】。
| |
|
| |
| Mukai等(1972)发现的平均生存力变化和生存力方差如图5.2所示。由于各品系第二染色体因突变发生与固定而产生分化,重复品系间的生存力方差随时间增加。此外,若有害突变比有利突变更普遍,则平均生存力会如预期般下降。实验结果与纯合时平均降低5%或更少生存力的有害突变模型一致。因此,该实验及其类似研究推动了图5.1所示的突变适应度谱理论框架。然而,目前仅在相对少数生物中开展过突变积累实验,且该方法本质上无法检测效应极小的突变或在表型测定环境中不影响表型的突变。例如,在拟南芥(''Arabidopsis thaliana'')化学诱导突变的研究中,Stearns和Fenster(2016)发现与生存力或繁殖力无直接关联的数量性状发生正向或负向变异的突变频率相等。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/a425819f39131fb532cd74ce429cf0976b00358d3e99f1014f20e0cfc87413e6.jpg]]<br />
| |
| '''图5.2''' Mukai等(1972)开展的黑腹果蝇经典突变积累实验结果。该实验维持了三组各含25个品系的突变积累群体。左图显示平均生存力随时间的变化,右图展示重复独立品系间方差的变化。每个数据点代表一组突变积累群体的测量值。任何类型的突变均导致遗传分化并增加方差。由于有害突变比有利突变更普遍,平均生存力随时间推移下降。资料来源:改绘自Mukai等(1972)图2。
| |
|
| |
| 在20个携带突变的品系中,有19个品系在自然生长条件下相比实验室优越环境表现出适应性降低。此外,不同分类群间突变适应度的分布可能存在差异。
| |
|
| |
| 在图5.1所示的突变适应度谱中,一个固有特征是'''有益突变'''比'''有害突变'''更为罕见。这使得估算有益突变的频率分布比估算有害突变的难度更大。尽管如此,已有若干研究直接测量了优势突变的影响(参见Eyre-Walker和Keightley 2007年的综述)。由于细菌种群世代时间短且易于构建和维持重复种群,它们常被用于突变研究。通过使用''E. coli'',多项研究表明,对适应度影响较小的有益突变比影响较大的突变更为普遍(Imhof和Schlotterer 2001;Rozen等 2002)。Sanjuan等(2004)利用核糖核酸(RNA)病毒,通过定点诱变技术产生大量单核苷酸突变。有益突变远少于有害突变,但检测到的8个有益突变的适应度平均提升了7%,且小效应突变更为常见。这些研究的一个重要注意事项是:检测到的有益突变偏向于较大效应的突变,因为极小的突变效应无法被测量;而较大效应的有益突变在自然选择下频率上升更快,从而更可能达到可检测的高频率。此外,在无重组的无性生物中,携带不同有益突变(相对于其突变前祖先)的谱系之间可能存在竞争,导致在平衡状态下只有最高适应度的谱系能固定,而其他谱系会消失。这种现象称为'''克隆干扰''',其避免是重组可能带来的适应度优势之一。
| |
|
| |
| 第三种估算有性世代突变率的方法随着快速且相对廉价的全基因组测序技术的普及而变得更加实用。通过直接比较亲本与子代之间,或家系中亲缘关系较远个体之间的长片段DNA序列,可以识别发生突变的核苷酸位点(Keightley等 2014;Narasimhan等 2017;Tatsumoto等 2017)。该方法需要组装好的参考基因组和深度测序覆盖度,因此目前主要应用于被深入研究的模式物种。
| |
|
| |
| ==== 突变率的演化 ====
| |
|
| |
| 早期的突变率估算依赖于表型效应或报告基因座来估计突变率。全基因组测序极大地扩展了在核苷酸水平观察突变的能力,从而提高了单倍体全基因组每代突变率(''U'')的估算精度,因为基因组的大部分区域可直接观测。直接测序技术也使得在日益多样化的分类群中估算突变率成为可能。表5.2展示了通过直接DNA测序获得的突变率估算值。不同调查分类群间的突变率存在差异,但在同一分类群内趋于更相似。原核生物的突变率中位数为<math display="inline">3.28\times{{10}^{-10}}</math>个核苷酸位点/代,范围从<math display="inline">2.34\times{{10}^{-8}}</math>到<math display="inline">7.9\times{{10}^{-11}}</math>;而真核生物的突变率中位数为<math display="inline">2.94\times{{10}^{-10}}</math>个核苷酸位点/代,范围从<math display="inline">8.15\times{{10}^{-10}}</math>到<math display="inline">7.61\times{{10}^{-12}}</math>(Katju和Bergthorsson 2019)。如预期所示,通过全基因组测序直接估算的全基因组突变率平均比表型估算值高125倍。
| |
|
| |
| 微卫星或简单序列重复(SSR)基因座的突变率也备受关注,因为这些基因座被广泛用作选择性中立的遗传标记来研究多种群体遗传过程(Hodel等2016;Vieira等2016)。这些重复DNA区域的突变率极高,介于每有性世代<math display="inline">1\times{{10}^{-2}}</math>到<math display="inline">6\times{{10}^{-6}}</math>之间(Ellegren 2000;Steinberg等2002;Beck等2003;Seyfert等2008;Marriage等2009)。SSR基因座的突变率还随重复基序(如AT或CA)和每个重复的碱基对数量(如二核苷酸或三核苷酸)而变化。
| |
|
| |
| <span id="突变率的演化-1"></span>
| |
| ==== 突变率的演化 ====
| |
|
| |
| 突变率本质上是细胞分裂和性生殖生物产生配子时维持与复制DNA的分子机制的产物。影响DNA错误相关细胞机制的基因座称为'''增变基因座'''(mutator loci)。一个增变基因座(如DNA聚合酶基因座)可能具有多个等位基因(或单倍型),每个等位基因通过不同的功能特性增加或减少其他基因座的突变发生。
| |
|
| |
| '''突变适合度谱'''(图5.1)显示,大多数突变是有害的,因此随时间推移新突变在群体中的积累会降低平均适合度。由此可预测,自然选择(以提高平均适合度为作用方向)将倾向于降低增变等位基因的频率,因为它们主要促进有害突变的产生。然而,重组的作用使这一预测更为复杂——重组会将增变基因座与携带其引发突变的其他基因座分离。因此,重组预计会减弱自然选择对增变基因座的影响,从而导致更高的突变率。
| |
|
| |
| 漂移屏障假说预测,突变率将进化至自然选择对突变等位基因作用所能达到的最低速率,且不同分类群间突变率的变异是遗传漂变强度差异的产物。如第7章将更充分阐述的,遗传漂变限制了基因型频率对自然选择的响应程度。当有效种群大小<math display="inline">(N_{e})</math>较小时,遗传漂变作用强,而自然选择(通过适合度差异<math display="inline">s</math>量化)仅能有效降低那些对突变率有显著影响的突变等位基因的频率。自然选择与遗传漂变达到平衡的临界点可定义为<math display="inline">4N_{e}s=1</math>。当<math display="inline">4N_{e}s{>}>1</math>时,突变等位基因的命运完全由遗传漂变决定——通常表现为随机丢失,但也存在偶然的随机固定。相反,当<math display="inline">4N_{e}s{<}<1</math>时,自然选择将导致突变等位基因趋于丢失。基于此推论,漂移屏障假说预测不同分类群的全基因组突变率应与有效种群大小<math display="inline">(N_{e})</math>相关。
| |
|
| |
| 表5.2 不同生物体每代每碱基对的自发突变率。这些估计值采用亲代与子代或其他近缘个体的比较、突变积累实验设计中的谱系比较,或通过波动分析估计重复样本间突变数的变异等方法获得。各研究均采用全基因组测序技术对基因组的大部分区域进行观测。
| |
|
| |
| {|
| |
| !width="28%"| Organism
| |
| !width="18%"| Mutation rate
| |
| !width="26%"| Method
| |
| !width="26%"| References
| |
| |-
| |
| | Bacteria
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | ''Escherichia coli''
| |
| | 2.2 × 10^-10
| |
| | Mutation accumulation
| |
| | Lee et al. (2012)
| |
| |-
| |
| | ''Mycobacterium smegmatis''
| |
| | 5.27 × 10^-10
| |
| | Mutation accumulation
| |
| | Kucukyildirim et al. (2016)
| |
| |-
| |
| | Eukaryota
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | Green alga (''Chlamydomonas''
| |
| | 9.63 × 10^-10
| |
| | Mutation accumulation
| |
| | Ness et al. (2015)
| |
| |-
| |
| | ''reinhardtii'')
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | Ciliate (''Tetrahymena thermophila'')
| |
| | 7.61 × 10^-12
| |
| | Mutation accumulation
| |
| | Long et al. (2016)
| |
| |-
| |
| | Mouse-ear cress (''Arabidopsis''
| |
| | 7.4 × 10^-9
| |
| | Parent-offspring comparison
| |
| | Yang et al. (2016)
| |
| |-
| |
| | ''thaliana'')
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | Animals
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | ''Drosophila melanogaster''
| |
| | 2.8 × 10^-9
| |
| | Parent-offspring comparison
| |
| | Keightley et al. (2014)
| |
| |-
| |
| | Midge (''Chironomus riparius'')
| |
| | 2.1 × 10^-9
| |
| | Mutation accumulation
| |
| | Oppold and Pfenninger
| |
| |-
| |
| |
| |
| |
| |
| |
| |
| | (2017)
| |
| |-
| |
| | Atlantic herring (''Clupea harengus'')
| |
| | 2.0 × 10^-9
| |
| | Parent-offspring comparison
| |
| | Feng et al. (2017)
| |
| |-
| |
| | Collared flycatcher (''Ficedula albicollis'')
| |
| | 4.6 × 10^-9
| |
| | Three generation pedigree
| |
| | Smeds et al. (2016)
| |
| |-
| |
| | Human
| |
| | 1.45 × 10^-8
| |
| | Related individuals
| |
| | Narasimhan et al. (2017)
| |
| |-
| |
| |
| |
| | 1.29 × 10^-8
| |
| | Parent-offspring comparison
| |
| | Jonsson et al. (2017)
| |
| |-
| |
| | Mouse
| |
| | 5.4 × 10^-9
| |
| | Mutation accumulation
| |
| | Uchimura et al. (2015)
| |
| |-
| |
| |
| |
| | 7.0 × 10^-9
| |
| | Mutation accumulation
| |
| | Ossowski et al. (2010)
| |
| |-
| |
| | Fungi
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | ''Saccharomyces cerevisiae''
| |
| | 1.7 × 10^-7
| |
| | Fluctuation assay
| |
| | Gou et al. (2019)
| |
| |-
| |
| | ''Schizosaccharomyces pombe''
| |
| | 2.0 × 10^-10
| |
| | Mutation accumulation
| |
| | Farlow et al. (2015)
| |
| |}
| |
|
| |
| 漂移屏障假说(【“drift barrier hypothesis”译为“漂移屏障假说”】)得到了多种物种突变率估算的实证模式以及群体遗传模型的支持(Kimura 1967;Lynch 2010, 2011)。如图5.3所示(Lynch et al. 2016综述),多个分类群的突变率估算值与有效种群大小呈负相关。这一规律同时适用于每个碱基对和全基因组水平的突变率,且两者呈正相关。漂移屏障假说也与以下模式一致:单细胞生物和微生物的突变率比有效种群较小(<math display="inline">N_{e}</math>)的脊椎动物低<math display="inline">10^{2}</math>至<math display="inline">10^{3}</math>倍,而前者具有更大的<math display="inline">N_{e}</math>。值得注意的是,如果突变率是自然选择为产生有利突变而优化的产物,那么突变率与有效种群大小应呈正相关,因为随着<math display="inline">N_{e}</math>的增加,自然选择的效力会增强。
| |
|
| |
| 在一项创新的早期研究中,Drake(1991,综述见Drake等1998)发现DNA基础的微生物中每个有效基因组(包含编码基因的基因组部分)的突变率为1/300。近期对更多类群的研究表明,多细胞真核生物并未表现出这种关系,而真细菌和单细胞真核生物中的负相关关系主要受单一分类单元结果的影响(Lynch等2016)。Drake观察到的每个有效基因组突变率的负相关模式也可以通过有效基因组大小与<math display="inline">N_{e}</math>之间的正相关性来解释。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/963285e65439cc717b31b8aab44f878fda0f20f4fb01b24faa60fcd64eab23f0.jpg]]<br />
| |
| '''图5.3''' 由于大多数突变是有害的,漂变屏障假说预测在有限种群大小的限制下,自然选择会将增变等位基因从种群中清除。对一系列分类单元每代每个碱基对的突变率(μ)和有效种群大小<math display="inline">(N_{e})</math>的经验估计显示了漂变屏障假说预测的负相关关系。资料来源:数据来自Lynch等2016。
| |
|
| |
| <span id="新突变的命运"></span>
| |
| ==== 5.2 新突变的命运 ====
| |
|
| |
| 中性或有益突变因孟德尔分离而丢失的概率。通过自然选择固定的突变。有限种群中突变等位基因的频率。扩张种群中的突变。无重组条件下穆勒氏齿轮导致有害突变的累积。
| |
|
| |
| 新突变引入种群后,其频率随时间如何变化?这个简单问题关乎理解新突变的固定与丢失概率,从而决定其在种群中的最终命运。突变率决定了新突变在种群中出现的频率。但一旦突变发生,作用于它的群体遗传过程将决定其频率的增减。本节将从遗传漂变和自然选择过程的四个不同视角探讨新突变的频率。这四种视角对新突变所处的种群背景(如有效种群大小、重组水平、突变的中性/有利/有害性)做出不同假设。显然,这些视角并未涵盖所有可能情境,而是旨在探索一系列可能性并展示多种确定新突变命运的不同方法。尽管本节将考虑自然选择对突变的作用,但所假设的简单选择形式应便于大多数读者理解。自然选择与适合度的严格定义将在第6章展开。
| |
|
| |
| ==== 突变因孟德尔分离而丢失的概率 ====
| |
|
| |
| 新突变的命运可以通过其孟德尔遗传模式进行追踪,正如R.A. Fisher在1930年所展示的(见Fisher 1999 variorum版)。将某基因座上所有现存等位基因记为<math display="inline">\mathrm{A}_{x}</math>,其中<math display="inline">x</math>为整数1,2,3…,x以索引不同等位基因,而新出现的选择中性突变为<math display="inline">\mathrm{A}_{\mathrm{m}}</math>。任何新突变最初都以单拷贝形式出现,因此必定存在于杂合基因型<math display="inline">\left(\mathrm{A}_{x}\mathrm{A}_{\mathrm{m}}\right)</math>中。为了形成下一代,该<math display="inline">\mathrm{A}_{x}\mathrm{A}_{\mathrm{m}}</math>杂合体会与群体中其他<math display="inline">\mathrm{A}_{x}\mathrm{A}_{x}</math>基因型随机交配。对于由<math display="inline">\mathrm{A}_{x}\mathrm{A}_{\mathrm{m}}</math>基因型产生的每个子代,有%的概率遗传突变等位基因,以及%的概率不遗传突变等位基因(此时传递的是<math display="inline">\mathrm{A}_{x}</math>等位基因)。
| |
|
| |
| <math display="inline">\mathrm{A}_{x}\mathrm{A}_{\mathrm{m}}</math>杂合体将突变等位基因传递到下一代的总概率取决于产生的子代数量。若<math display="inline">k</math>表示由<math display="inline">\mathrm{A}_{x}\mathrm{A}_{\mathrm{m}}</math>杂合体产生的子代数,且等位基因独立分配,则
| |
|
| |
| <math display="block">
| |
| \mathrm{P(突变丢失)}=\left({\frac{1}{2}}\right)^{k}
| |
| </math>
| |
|
| |
| 表示突变等位基因在所有子代中均未被传递到下一代的概率。正如预期,随着子代数增加,突变等位基因未被传递的概率会下降。
| |
|
| |
| 在规模保持恒定的群体中,每对亲本平均产生两个子代以维持世代更替。此处关键短语是”平均”,意味着并非每对亲本都会产生两个子代:有些亲本会产生更多子代,有些则更少。如第3章方差有效种群大小所述,泊松分布常用于模拟繁殖成功率的变异。这里我们同样可以使用泊松分布来确定平均家系大小为两个子代时,各家庭规模的期望频率(表5.3)。需要了解不同家庭规模的期望比例,是因为每个家庭规模对应不同的突变等位基因未传递概率。
| |
|
| |
| 对于特定家庭规模<math display="inline">k</math>,突变等位基因未被传递到下一代的概率是亲本对期望频率与突变等位基因未传递概率的乘积:
| |
|
| |
| 表5.3 平均家系大小为二<math display="inline">(\overline{{k}}=2)</math>时,泊松分布下每对亲本各家庭规模(k)的期望频率。同时给出不同家庭规模下突变等位基因<math display="inline">\mathsf{A}_{\mathsf{m}}</math>未被传递到任何子代的期望概率。注意0!等于一。
| |
|
| |
| <pre class="markdown">| 每对亲本的家庭规模(k) | 0 | 1 | 2 | 3 | 4 | | K |
| |
| |------------------------|-----|-------|---------|----------|---------|----|-----------|
| |
| | 期望频率 | e² | 2e⁻² | 2e⁻² | 4 -3 Y | 2³ | | \(\frac{2^k e^{-2}}{k!}\) |
| |
| | 突变等位基因未传递的概率 | 1 | 1 - ½ | \(\left(\frac{1}{2}\right)^2\) | \(\left(\frac{1}{2}\right)^3\) | \(\left(\frac{1}{2}\right)^4\) | | |
| |
|
| |
| $$
| |
| P(\mathrm{mutant~lost})=\left(\frac{2^{k}}{k!}\right)e^{-2}\left(\frac{1}{2}\right)^{k}
| |
| $$
| |
|
| |
| 即表5.3中各列两项的乘积。突变等位基因未被传递到下一代的总体概率是所有可能家庭规模(从0到无穷大)的概率之和:
| |
|
| |
| $$
| |
| P(\mathrm{mutant~lost})=\sum_{k=0}^{\infty}\left(\frac{2^{k}}{k!}\right)e^{-2}\left(\frac{1}{2}\right)^{k}
| |
| $$
| |
|
| |
| 尽管这个求和式看似复杂,但实际上可以简化为一个优雅的结果。将常数项\(e^{-2}\)提到求和符号前:
| |
|
| |
| $$
| |
| P(\mathrm{mutant~lost})=e^{-2}\sum_{k=0}^{\infty}\left(\frac{2^{k}}{k!}\right)\left(\frac{1}{2}\right)^{k}
| |
| $$
| |
|
| |
| 此时\(2^{k}\)与\(\left(\frac{1}{2}\right)^{k}\)相互抵消,得到:
| |
|
| |
| $$
| |
| P(\mathrm{mutant~lost})=e^{-2}\sum_{k=0}^{\infty}\frac{1}{k!}
| |
| $$
| |
|
| |
| 最终的关键在于识别级数\(1+1+\frac{1}{2!}+\frac{1}{3!}+\cdots+\frac{1}{k!}\)当\(k\)趋近无穷大时收敛于\(e\)(\(e=2.718\ldots\))。因此求和项可替换为\(e\):
| |
|
| |
| $$
| |
| P(\mathrm{mutant~lost})=e^{-2}e=e^{-1}
| |
| $$
| |
|
| |
| 如预期所示,新突变仅因孟德尔式分离在一代内丢失的概率为\(e^{-1}=0.3\bar{6}7\bar{9}\)。这意味着新突变约有36%的概率在其进入群体后的第一代即被丢失。新突变的生存环境异常严酷!
| |
|
| |
| 此结果可扩展至多代孟德尔式分离下的突变丢失概率。突变随时间推移从群体中丢失的累积概率通式为:
| |
|
| |
| $$
| |
| P(\mathrm{mutant~lost~generation~}t)=e^{x-1}
| |
| $$
| |
|
| |
| 其中\(x\)为第\(t-1\)代或之前世代的丢失概率。(公式5.7中的求和级数实质为\(1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots+\frac{x^{k}}{k!}\),当\(k\)趋近无穷大时收敛于\(e^{1+x}\),从而得到\((e^{-2})(e^{1+x})=e^{x-1}\)。当突变首次出现时\(x=0\)。)
| |
|
| |
| 应用此结果可得:突变在两代内丢失的概率为\(e^{-0.6321}=0.5315\),三代内丢失概率为\(e^{-0.4685}=0.6295\)。图5.4基于此递推关系展示了新突变在140代内的丢失概率。该图的结论表明:给定足够时间,新突变终将从群体中消失。
| |
|
| |
| </pre>
| |
| 图 5.4 新突变因孟德尔分离从种群中丢失的概率。中性等位基因最终会从种群中消失,而有利突变的固定概率约为其选择优势的两倍。随时间累积的概率由 <math display="inline">e^{c(x-1)}</math> 描述,其中 <math display="inline">x</math> 是前一代的丢失概率,<math display="inline">c</math> 为选择优势程度(若有)。该期望概率假设种群无限大且家系大小的方差服从泊松分布。
| |
|
| |
| 我们还可以探究自然选择对”新突变终将丢失”这一预测的影响。假设一个新突变具有微弱有利性而非中性。自然选择将提高该突变传递到下一代的几率,使其相对于种群中其他等位基因具有微弱优势。令 <math display="inline">c</math> 表示新突变的选择优势,1.0 表示中性,1.01 则表示传递优势为 <math display="inline">1\%</math>。则等位基因在第 <math display="inline">t</math> 代丢失的累积概率为:
| |
|
| |
| <math display="block">
| |
| P({\mathrm{mutant~lost~generation~}}t)=e^{c(x-1)}
| |
| </math>
| |
|
| |
| 该方程版本将中性情况下的指数乘以有利等位基因的选择优势。若仅经过少数世代,这对突变丢失概率的影响微乎其微,但随着世代数增加差异会扩大(图 5.3)。一般而言,新有利突变未被丢失的概率约为其选择优势的两倍——对于现实中较小的选择优势值而言,这仍是极低的概率。然而正如费舍尔指出的,若类似250个独立有利突变随时间逐个出现,则所有突变在孟德尔分离过程中丢失的概率极低(<math display="inline">0.98^{250}=0.0064</math>)。这表明随着突变持续产生,至少部分有利突变将在种群中确立。
| |
|
| |
| “新中性突变必然永久丢失”的结论似乎与遗传漂变导致新突变随机固定的可能性相矛盾。费舍尔模拟新突变命运的方法假设种群规模极大。该假设允许使用泊松分布下各家系大小亲本对比例的期望值,以及各家系大小的等位基因丢失概率——这些概率仅在覆盖广泛家系大小的众多亲本对极限情况下成立。有限数量的亲本对可能因期望值的随机偏离而无法满足这些预期。无限种群规模的假设是合理的,因其用于揭示:即使完全不存在遗传漂变,颗粒遗传本身即可导致新突变的丢失。接下来我们将探讨有限种群中新突变的命运。
| |
|
| |
| ==== 有限种群中新突变的命运 ====
| |
|
| |
| 关于新突变的第二种视角是将其命运视为有限群体中无自然选择作用下的等位基因。我们可以运用第3章中发展的'''遗传漂变'''(genetic drift)概念和模型来预测新突变在群体中随时间推移的频率变化。第一个关键观察是认识到任何新突变的初始频率即为:
| |
|
| |
| <math display="block">
| |
| p_{0}(\mathrm{newmutation})=\frac{1}{2N_{e}}
| |
| </math>
| |
|
| |
| 因为新突变在包含<math display="inline">2N_{e}</math>个等位基因拷贝的群体中以单拷贝形式存在。若新突变的频率完全由遗传漂变决定,则每个新突变每代被固定的概率为<math display="inline">\frac{1}{2N_{e}}</math>,丢失的概率为<math display="inline">1-\frac{1}{2N_{e}}</math>。这一结果符合直觉——新突变极为罕见,更接近丢失而非固定状态。同时表明新突变的固定或丢失概率取决于有效群体大小。
| |
|
| |
| 通过遗传漂变的扩散近似(diffusion approximation),可估算新突变被固定或丢失前的平均世代数(Kimura和Ohta 1969a)。图3.14与式3.40给出了取决于有效群体大小和初始频率的等位基因被固定或丢失的平均世代数。在有效群体规模较大的假设下,最终被固定的等位基因平均需要<math display="inline">4N_{e}</math>代完成固定;而丢失的等位基因所需世代数少得多,随着群体规模增大和初始频率<math display="inline">\frac{1}{2N_{e}}</math>减小,丢失所需世代趋近于零。然而,由于遗传漂变是随机过程,固定或丢失时间的平均值的方差预期会很大。换言之,每个新突变的等位基因频率将在0到1之间随机游走。虽然许多突变可能迅速丢失,但其他突变可能在丢失或固定前持续分离数个甚至多个世代。
| |
|
| |
| 新突变的命运可通过模拟直观呈现。图5.5展示了在<math display="inline">N_{e}=10</math>群体中每30代引入的新突变频率变化。引入的七个突变中有六个丢失,仅一个固定。这与<math display="inline">N_{e}=10</math>群体中约1/20新突变将被固定的预测基本吻合。多数丢失突变在10代内消失;
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/0bde1db90c80b9ed1a8c66adcff13594f6bd4915c410cfbdbc9ded051e89085b.jpg]]<br />
| |
| 图5.5 初始频率为<math display="inline">\frac{1}{2N_{e}}</math>的新突变随时间变化的频率。本例中每30代向群体引入一个新突变,<math display="inline">N_{e}=10</math>。除一条实线表示的突变外,所有突变均在数代内丢失。唯一被固定的等位基因相较于丢失所需时间经历了更长的过程。模拟开始时祖先等位基因频率为1(未显示)。当新突变达到固定时,原始祖先等位基因丢失,新突变成为祖先等位基因。
| |
|
| |
| 尽管在一个案例中,该突变持续分离了约25代。公式3.40预测突变平均约在六代内丢失,与模拟结果大致一致。达到固定的突变在60代内完成,其等位基因频率呈现曲折的轨迹。公式3.40预测当<math display="inline">N_{e}=10</math>时,达到固定的突变平均需要约39代,表明模拟结果略高于预期的平均固定时间。
| |
|
| |
| <span id="互动框5.1-有限群体中中性突变的频率"></span>
| |
| = 互动框5.1 有限群体中中性突变的频率 =
| |
|
| |
| 通过文本模拟网站可以观察受遗传漂变影响的新突变频率。
| |
|
| |
| 首先关注标记为”严格中性”的顶部图表组。初次使用默认参数运行模拟以了解输出结果。右侧大图和左侧两个小图分别显示什么?
| |
|
| |
| 接下来,使用默认参数运行模拟:每20代引入一次突变,共200代,群体规模<math display="inline">N_{e}=20</math>,500个独立重复位点。有多少突变达到固定或丢失(查看小直方图)?固定或丢失的平均时间是多少?预期达到固定或丢失的新突变数量如何?这些预期与模拟结果相比如何?将群体规模增至<math display="inline">N_{e}=50</math>并观察500代。达到固定和丢失的新突变数量如何变化?新突变的分离时间如何变化?
| |
|
| |
| 这些关于中性突变在遗传漂变下频率与命运的预测表明,群体中至少部分遗传变异得以维持,仅因新突变在达到固定或丢失前经历的随机等位基因频率游走。若在单个时间点观察图5.4中的群体,由于新突变可能正处于固定与丢失之间的某个阶段,群体可能呈现多态性。若同时观察许多这样的位点,极有可能至少部分位点会呈现多态性。这一观察构成了分子进化中性理论的基础——该假说认为群体遗传变异由遗传漂变引起,详见第8章。
| |
|
| |
| ==== 扩张群体中的突变 ====
| |
|
| |
| 关于新突变命运的第三个视角聚焦于扩张群体。发生在扩张群体边缘的新突变可能丢失,也可能达到高频率并取代现有等位基因。当突变从起源点沿扩张群体的前沿在频率上增加并空间扩散时,被称为”冲浪”,这一现象由Edmonds等(2004)首次展示。冲浪突变的演化动态与恒定规模群体内发生的突变不同。中性、有利或有害突变均可表现冲浪行为。突变冲浪为等位基因频率渐变群(地理梯度)和经历过群体扩张物种的多态性空间分布模式提供了可能的解释(Excoffier等(2009b)综述)。
| |
|
| |
| 突变冲浪可以通过二维网格模拟来表征一个扩张的种群,如图5.6所示。网格中的每个单元格代表一个空间位置,可容纳一定数量的个体,最大数量为单元格的承载能力(<math display="inline">K</math>)。每个单元格内的单倍体个体通过生成符合泊松分布的子代进行繁殖,该分布的均值为<math display="inline">λ</math>。在每个世代中,若单元格内个体数量超过<math display="inline">K</math>,则通过随机淘汰维持承载能力。每个世代的最后一步是以迁移率<math display="inline">m</math>进行迁移,来自给定单元格的迁移者以相同概率移动到相邻单元格。为模拟中性突变,可设置多个具有相同家族大小均值(<math display="inline">λ</math>)的单倍型;为模拟自然选择,适应性较低的单倍型具有较小的家族大小均值(较小<math display="inline">λ</math>),而适应性较高的单倍型具有较大的家族大小均值(较大<math display="inline">λ</math>)。在此类模型中,种群将扩张并填满网格中未被占据的单元格。携带新突变的单倍型将经历多种形式的遗传漂变——包括家族大小的随机变异、承载能力限制下的随机抽样以及迁移过程中的随机抽样。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/c5dd003be30c1d88b1890754d351c176f22924684c688f0714bbb4a8a14b4fd5.jpg]]<br />
| |
| 图5.6 突变冲浪的假设性示例。左侧为<math display="inline">3\times9</math>网格中随时间变化的人口密度,右侧为单倍型频率。种群最初由位于网格左边缘的一个达到承载能力<math display="inline">K</math>的单元格建立。创始单元格中的个体繁殖后,其后代通过扩散在未占据单元格中定居。种群向右扩张并最终使多数单元格达到其承载能力。初始时所有个体均携带原始单倍型,但某一时刻单个个体发生了突变。此案例展示了突变冲浪现象:随着种群持续向右扩张并占据可用单元格,该突变持续存在并达到高频率。新突变在繁殖、维持承载能力的淘汰过程以及迁移过程中均受到遗传漂变作用。通过迁移,携带高频率冲浪突变的单倍型也可向起源位置左侧扩散,当新突变的适应度高于原始单倍型时更易出现此模式。
| |
|
| |
| Miller(2010)研究表明,在一维种群中,中性突变“冲浪”的概率与平均家庭大小(λ)呈正相关,但与环境容纳量(K)和迁移率(m)呈负相关。前两个模式可通过遗传漂变理解——随着平均家庭大小的增加,由于家庭大小的方差也增加,遗传漂变增强;而通过淘汰作用,随着环境容纳量的减少,遗传漂变也会增强。迁移率降低导致冲浪概率增加的原因是:携带突变单倍型的个体能完全占据一个细胞,而较少与位于种群扩张前沿后方非突变个体混合。
| |
|
| |
| 在二维网格中,中性突变冲浪的概率与平均家庭大小(λ)和环境容纳量(K)关系较弱,与迁移率(m)无关。Miller(2010)对迁移率与冲浪关系微弱的现象提出两种解释:其一,突变仅被建模在种群扩张前沿,此时含突变的细胞周围是空置或低密度细胞,与突变率无关;其二,当不同单倍型沿着扩张种群边缘的锯齿状空间边界共存时,新突变会失去其空间“先发优势”,冲浪概率降低(另见Klopfstein等2006;Hallatschek等2007;Lehe等2012)。
| |
|
| |
| 突变冲浪的实证证据呈现多种形式。琼脂平板上培养的细菌种群被直接用于研究突变冲浪。Hallatschek等(2007)使用能产生可见蛋白标记的细菌和酵母菌株,证明扩张种群中的遗传漂变常导致单一菌株在平板扇形区域扩散而少有菌株混合。(教材网站提供Hallatschek等2007论文中视觉冲击力强的图片链接。)Bosshard等(2017)同样利用细菌种群证明,与大型、充分混合的种群相比,种群扩张会导致有害突变频率更高。该研究支持有害突变可通过突变冲浪积累的预测(Travis等2007),这种现象被称为扩张负荷(expansion load),以明确其作为遗传负荷的特殊成因(Peischl等2013;Peischl和Excoffier 2015)。细菌研究还表明,冲浪可增加轻微有益等位基因的固定率,并提升适应速率(Gralka等2016)。隐性有害等位基因频率随地理距离(距非洲)增加的现象与扩张负荷一致,这一模式支持人类种群扩张过程中可能发生突变冲浪的观点(Hallatschek等2007;Peischel等2016)。
| |
|
| |
| ==== 自然选择固定突变的几何模型 ====
| |
|
| |
| 关于新突变命运的第四个视角将聚焦于有利突变,首先关注仅通过自然选择固定的突变,其次考察由自然选择和遗传漂变共同作用而固定的突变。除了考虑新突变在分离过程中如何丢失外,Fisher在1930年(参见Fisher 1999年变体版)构建了另一个关于受自然选择作用影响的突变命运的模型。如本章前文所述,突变可能对适合度产生一系列影响,也可能对具有遗传基础变异的表型产生影响。Fisher建立的模型试图确定随时间推移被自然选择固定的有利突变效应大小的范围或分布。被自然选择固定的突变是具有大效应还是小效应?或者它们的效应大小是否遵循某种分布模式?你很可能知晓该模型的普遍结论,却不了解这些结论的来源或其背后的假设。其普遍结论是:有利突变具有小效应——我们不应期望有利变化通过单个巨大飞跃实现。这种进化观被称为'''微突变主义(micromutationalism)''',该概念在进化生物学和群体遗传学中产生了深远影响(参见<math display="inline">\mathrm{Orr~1998}</math>及其参考文献)。推导出该结论的模型被称为'''突变的几何模型''',本节将详细阐述该模型。
| |
|
| |
| '''微突变主义(Micromutationalism)''':认为通过自然选择过程固定的有利突变具有小效应,因此适应过程以渐进遗传变化为特征的观点。
| |
|
| |
| Fisher设想了一种情景:两个表型值决定了个体生物的生存与繁殖能力(即适合度,适合度将在第六章严格定义)。例如,某植物物种可能通过叶片数量和叶片大小这两个表型来实现光合作用的最大光捕获量。然而在模型中,只要表型对个体适合度有贡献,其具体性质并不重要。需要理解的关键点是:越接近最大适合度值(Fisher称之为”最适点”)的表型值越受自然选择青睐,这使得赋予更高适合度表型的基因型频率随时间推移在种群中增加并固定。图5.7展示了该模型:两个性状值由坐标轴表示,两个性状组合的最适适合度值位于中心标有O(optimum)的位置。
| |
|
| |
| 假设某个个体的两种表型值使其位于表型轴上的点A,距离最适适应度的距离为<math display="inline">r</math>。以最适点为中心、半径为<math display="inline">r</math>的圆上所有点(图5.5A中虚线圆)都具有与该个体相同的适应度。接下来假设该个体基因型的某个等位基因可能发生随机突变。若突变效应是随机的,则突变可能导致表型从点A向任意方向移动,这些移动的距离可近可远。有些突变使表型移动较短距离,有些则导致长距离移动;有些突变使表型朝最适点靠近,有些则使其远离最适点。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/56a6a2a186492e404717060ce907bbeddeb3f88b8979a188593df40a019b39eb.jpg]]<br />
| |
| 图5.7 R. A. Fisher的几何模型描述自然选择固定突变的过程。图A显示两个假设表型轴,其适应度由中心红点处的表型值达到最大。个体(或种群平均表型)的表型值距离最大适应度点有一定距离。虚线圆表示围绕最大适应度点的等适应度边界。本示例仅用两个表型定义适应度,若有三个表型则为球体,<math display="inline">n</math>个表型则为<math display="inline">n</math>维高维空间。图B显示两种具有较小或较大表型效应的突变。突变的表型效应可在当前表型周围任意方向(实线圆半径为<math display="inline">m</math>)。较小效应的突变更可能使表型朝最大适应度移动(突变效应圆左侧区域更多地位于等适应度虚线内侧)。
| |
|
| |
| 通过这个几何模型,我们能否确定哪些类型的突变更可能被自然选择固定并促进适应演化?该模型得出一个重要结论:表型效应极大的突变(表型改变超过2r)即使方向正确也无法使表型更接近最适点。由于这类突变总是将表型移至虚线圆外的低适应度区域,它们永远不会被自然选择固定。
| |
|
| |
| 那么效应较小的突变又如何呢?图5.5B展示了两种表型效应较小的突变情况(表型变化小于2r)。右侧是表型效应较大的突变,左侧是表型效应较小的突变。这两种突变可能发生在任何方向,通过以A为中心、半径<math display="inline">m</math>的圆来表征突变效应的量级。值得注意的是,随着突变效应增大,描述表型效应的圆落在虚线圆(表征个体在A点当前适合度)内部的比例会减少。当突变的表型效应趋近于零时(<math display="inline">m\rightarrow0</math>),其效应圆将接近一半位于当前适合度圆弧内,一半位于圆弧外。换句话说,随着突变的表型效应逐渐增大,其效应圆覆盖当前适合度圆弧外的区域会越来越多。突变表型效应越大,其朝降低适合度方向改变的概率也越高。因此,自然选择应更倾向于固定小效应突变而非大效应突变,因为小效应突变有更高概率使表型值向最优点移动。效应趋近于零的突变有接近1/2的概率是有利的,而大效应突变的有利概率则逐渐降低。
| |
|
| |
| 这可以用以下方程描述:
| |
|
| |
| <math display="block">
| |
| P({\mathrm{mutation~improves~fitness}})={\frac{1}{2}}\left(1-{\frac{m}{2r}}\right)
| |
| </math>
| |
|
| |
| 其中<math display="inline">m</math>表示突变的表型效应半径,<math display="inline">r</math>表示当前表型值与最优点之间的距离。当<math display="inline">m</math>趋近于零时,突变使表型更接近最优点的概率趋近于1/2。随着突变效应增大,其提升适合度的概率逐渐降低。当<math display="inline">m</math>等于<math display="inline">2r</math>时,突变完全无法提升适合度:此时<math display="inline">2r</math>效应的突变最多只能将A点重新定位到最优点周围等适合度圆的对侧。
| |
|
| |
| Fisher还指出,生物体的适合度取决于许多独立性状,因为生物体的表型必须满足生长、摄食、逃避捕食、交配等多重需求。因此他认为,图5.5中用于说明的等适合度虚线圆实际上更应被理解为多维空间中的超球面。在<math display="inline">n</math>维空间中,判断突变效应相对于最优点距离<math display="inline">(r)</math>的大小时,需用<math display="inline">{\frac{r}{\frac{2r}{\sqrt{n}}}}=r{\frac{\sqrt{n}}{2r}}</math>代替式5.12中的<math display="inline">m/2r</math>。核心结论是:表型维度增加会导致突变提升适合度的概率随其表型效应增大而更快下降。图5.8上部绘制了式5.12的变体(假设适合度由多个独立表型决定),展示了多维表型效应下突变提升适合度的概率分布。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/71c5bfce4839bceb7a486af1995147873369d1ec97ae8893e1a5eaf4154bbfe0.jpg]]<br />
| |
| 图 5.8 突变被自然选择固定的概率取决于其对适合度的影响幅度。通过使用突变的几何模型并假设适合度由多个表型决定,Fisher指出当突变效应趋近于零时,突变提升适合度的概率接近二分之一(顶部)。这一结果源于较小突变比较突变更有机会使表型向最优点移动(见图 5.4)。木村资生指出,对适合度影响较小的突变也最可能因遗传漂变而非自然选择被固定或丢失。综合考量突变使表型向更高适合度方向移动的概率,以及突变具有足够大的适合度差异以逃逸遗传漂变的概率,表明中等效应的突变最可能被自然选择固定(底部)。两个模型均假设对适合度有任何影响的突变具有相同的发生概率。
| |
|
| |
| 突变几何模型的结论在图 5.6 的顶部面板中显而易见。小效应突变最有可能使生物体更接近其适合度最优值,因此最可能被自然选择固定。较大效应的突变具有较低的概率改善适合度,因此更不易被自然选择固定。Fisher将此情形类比显微镜的焦距调节:若显微镜已接近对焦状态,随机的大幅度调节更可能使成像变差,而随机的小幅度调节更可能改善对焦。Fisher模型的一个逻辑推论是,当突变效应趋近于零时,突变的适合度谱将趋近于 <math display="inline">50\%</math> 有害突变和 <math display="inline">50\%</math> 有益突变。这一预测与图 5.1 中突变适合度谱的总体情况并不一致。
| |
|
| |
| 多年后,木村资生(Kimura 1983)通过放宽费舍尔(Fisher)关于无限有效种群大小的隐含假设,重新评估了'''突变几何模型'''(geometric model of mutation)的预测。这一改变使得'''遗传漂变'''(genetic drift)能够与自然选择共同作用于突变频率。在有限种群中,等位基因频率由抽样误差和自然选择对高平均适合度等位基因的固定效应共同决定。只有当自然选择的力量强于遗传漂变的随机化效应时,自然选择才会决定某个等位基因的命运。自然选择的压力还取决于突变的表型效应——效应较大的突变会经历更强的定向固定推动力。因此,自然选择对'''效应最大'''的新突变具有最强的定向固定推动力。换言之,效应较小的新突变更可能经历遗传漂变导致的随机固定或丢失。图5.8的下图显示了有限种群中新突变被自然选择固定的概率。表型效应最小的突变仍最可能使表型向高适合度方向移动。然而,这一过程现在受到遗传漂变效应的平衡,后者对适合度效应微弱的新突变影响最大。修正后的结果表明,在有限种群的自然选择下,对适合度具有'''中等效应'''的新突变最可能被固定。
| |
|
| |
| 奥尔(Orr 1998)分析了有限种群中经自然选择固定的突变效应大小,并校正了随时间推移种群接近最大适合度时突变效应必然减小的现象。自然选择与遗传漂变的净平衡将在后续章节详细讨论,而位点与等位基因的表型效应将在第9章'''数量遗传学'''(quantitative genetics)中深入探讨。
| |
|
| |
| <span id="muller-s-ratchet与有害突变的固定"></span>
| |
| ==== Muller s ratchet与有害突变的固定 ====
| |
|
| |
| 关于新突变命运的最后一个视角聚焦于'''缺乏重组'''的基因组中发生的'''有害突变'''(deleterious mutations)。突变、遗传漂变和自然选择的共同作用导致种群中”突变最少”的基因型类群逐渐消失,这种现象称为'''穆勒氏棘轮'''(Muller s Ratchet)(Muller 1964;Maynard Smith 1978;Charlesworth and Charlesworth 1997)。该名称类比于仅允许单向转动的机械装置(如棘轮扳手)。穆勒氏棘轮导致种群中突变不断积累,若大多数突变有害,则种群平均适合度将持续下降。因此,穆勒氏棘轮揭示了某些条件下重组的'''选择优势'''(selective advantage)。该机制与'''希尔-罗伯逊效应'''(Hill-Robertson effect)(Hill and Robertson 1966)密切相关——当自然选择对众多具有独立适合度值的位点作用较弱时,由于重组减少和遗传漂变导致的连锁不平衡,选择效力会被削弱(Comeron et al. 2008综述)。
| |
|
| |
| 要详细了解'''Muller’s Ratchet'''的作用机制,可考虑一个有限规模的单倍体(haploid)克隆繁殖种群。假设所有位点的突变均具有同等有害性,且受到自然选择(natural selection)相同程度的抵制。每个突变位点的选择劣势为<math display="inline">s</math>,而携带<math display="inline">n</math>个突变位点的个体总选择系数为<math display="inline">\left(1-s\right)^{n}</math>。此外,假设突变不可逆——仅能从野生型等位基因(wild-type alleles)产生有害等位基因(deleterious alleles),而无法从有害等位基因恢复为野生型。最初,种群中所有个体均无突变。新发生的突变会减少无突变个体的比例,并增加携带<math display="inline">1,2,3\dots n</math>个突变的个体频率。随着时间推移,零突变类别的频率下降,而携带一个或多个突变个体的频率上升。这一过程如图5.9的上部两个面板所示。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/eddf52ffaa9ce3072fb6cee412f7d0e655b4756a73d5c44c33e0f615ce84a50a.jpg]]<br />
| |
| '''图5.9''' 模拟结果展示了无重组情况下'''Muller’s Ratchet'''增加有害突变数量的作用。初始时,种群中所有单倍体个体的突变数为零。随时间推移,突变随机发生并持续减少低突变数量个体的频率。遗传漂变(genetic drift)导致抽样误差,并使个体数量较少的突变类别随机丢失。携带更多突变的个体因自然选择对有害等位基因的抵制而更不易繁殖。一旦最低突变类别(如零突变类)因遗传漂变和突变而丢失,便再无机制可重建该类。因此,突变数量的分布持续右移而无法左移。模拟参数为<math display="inline">N_{e}=200,\upmu=0.06</math>,每个突变使繁殖概率降低<math display="inline">1\%</math>,且每个个体有100个位点。
| |
|
| |
| 遗传漂变和自然选择与突变共同作用于不同突变数量个体的频率。遗传漂变的抽样误差可导致种群中低频突变类别的随机性丢失。遗传漂变的这一效应不受突变数量影响。任何因漂变丢失的突变类别均可通过低突变数量个体的突变重建。然而,当种群中所有最低突变数量的个体丢失后,该最低突变类别将永久消失。这是因为突变无法产生可减少有害突变数量的野生型等位基因。此外,由于无重组作用,最低突变类别也无法重组恢复。遗传漂变的整体效应是推动突变数量的频率分布向更高数值移动。相比之下,自然选择倾向于使突变数量分布向更低数值移动,因为携带更多突变的个体会越来越受自然选择抵制。
| |
|
| |
| 如果有效种群大小较小,穆勒氏棘轮还会导致在具有最少突变的个体类别中,单个等位基因的固定速率加快。这是因为具有最少突变的类别不会通过突变得到更新。该类别是有限的,且由具有相同适应度的等位基因组成,因此遗传漂变最终会导致该突变类别内单个等位基因的固定。这种效应对重组水平低的基因组或在交配系统导致高纯合度从而实质上抵消重组的二倍体种群具有重要影响。在这些情况下,固定速率可能高于具有自由重组且有效种群大小相同的基因组中有害突变的固定速率(参见Charlesworth和Charlesworth 1997)。
| |
|
| |
| <span id="交互框5.2-穆勒氏棘轮"></span>
| |
| === 交互框5.2 穆勒氏棘轮 ===
| |
|
| |
| 访问教材网站查看穆勒氏棘轮模型的模拟:该模型展示了无重组情况下,遗传漂变和自然选择对新的有害突变的影响。
| |
|
| |
| 模拟开始时,种群由无突变的单倍体克隆个体组成,随后让突变、遗传漂变和自然选择发挥作用。每个个体的适应度决定其向下一代贡献后代的机会。每个个体产生的后代数量服从泊松分布(平均值为1个子代,“平均家系大小”和”最大家系大小”参数可调整此分布)。模拟中可设置有效种群大小、针对有害突变的选择系数(每个突变导致的存活率下降百分比)以及突变率。结果以种群中具有特定突变数量的个体比例呈现。
| |
|
| |
| 首先使用默认参数运行模拟。然后尝试单独增加有效种群大小(或单倍体染色体种群大小)、针对有害突变的选择系数以及突变率。在更改每个参数前,预测这些模拟参数对基因组突变数频率分布的影响。
| |
|
| |
| <span id="突变模型"></span>
| |
| ==== 5.3 突变模型 ====
| |
|
| |
| 无限等位模型、<math display="inline">k</math>等位模型和逐步突变模型。<br />
| |
| 使用标准遗传距离和<math display="inline">R_{ST}</math>理解突变模型的生物学意义。<br />
| |
| 适用于DNA序列的无限位点模型和有限位点突变模型。
| |
|
| |
| 突变以多种方式作用,并能在等位基因和DNA序列层面产生广泛的变化。为研究突变的等位基因频率效应,构建一些简化的突变过程模型是有益的。突变模型试图捕捉突变引起的遗传变化本质,同时将突变过程简化为允许对等位基因频率变化进行概括的形式。并不存在单一的突变过程模型,而是一系列模型用于封装不同类型基因座和等位基因的突变过程特征。通常,突变模型的建立受到同工酶电泳或DNA测序等分子方法的启发,这些方法用于检测实际种群中的遗传变异。本节介绍并描述主要的突变模型类别。两种离散等位基因的突变模型被应用于衡量种群间遗传差异,以展示突变模型在解释遗传差异中的作用。DNA序列的突变模型将应用于本章最后一节关于谱系分支模型中突变的讨论。
| |
|
| |
| ==== 离散等位基因的突变模型 ====
| |
|
| |
| 前几章反复出现的主题是在不同群体遗传过程下预测纯合性与杂合性(自源同型与异源同型)的期望水平。这些预测中许多关键假设是:状态同一性可被视为血统同一性。换言之,状态相同的等位基因之所以相似,是因为它们过去某个时刻源自一个共同的祖先等位基因拷贝。突变的无限等位基因模型(见Kimura和Crow 1964)就是用于保证状态同一性等同于血统同一性的假设。在无限等位基因模型下,每次突变事件都会产生一个与种群中现有任何其他等位基因不同的新等位基因。某个特定等位基因状态一旦通过突变首次产生,就永远不可能再次通过突变产生。本质上,该等位基因状态将从可能的突变列表中永久移除。无限等位基因模型旨在避免两种等位基因具有状态同一性但缺乏血统同一性的可能性,这种情况可能在相同等位基因随时间反复通过突变产生时发生。在无限等位基因模型下,突变仅产生每个等位基因的原始拷贝,而不会作为持续过程影响种群中已有等位基因的频率。等位基因存在于种群后,其频率变化由突变以外的其他过程决定。另一个推论是:由于所有等位基因都通过单次突变事件产生且等位基因永远不会积累多次突变,所有等位基因间的进化”距离”或转变事件数量是相同的。这意味着在估计杂合性或固定指数时,所有等位基因可被视为等同的。
| |
|
| |
| 无限等位模型(''infinite alleles model'')可能大致近似于分子标记(如同工酶【“allozymes”译为“同工酶”】)的突变过程,因为等位基因呈现离散状态(例如在凝胶上的快速或慢速迁移)且同工酶位点通常被观察到具有低突变率,因此样本中的大多数等位基因不太可能是近期突变的产物。一段DNA序列也可能近似于无限等位模型。在500个核苷酸的序列中,存在<math display="inline">4^{500}=1.072\times10^{301}</math>种独特的核苷酸组合。如果突变完全随机且以等概率将现有核苷酸改变为任何其他核苷酸,则DNA序列群体中可能发生多次突变而不会产生重复等位基因,因为可能的等位基因数量确实极其庞大。
| |
|
| |
| '''同塑性(Homoplasy)''':指等位基因状态相同但非血统同一性(''identity by descent'')的现象。<br />
| |
| '''无限等位模型(Infinite alleles model)''':假设每次突变事件都产生一个与群体中现有所有等位基因不同的新等位基因,因此两个或多个等位基因的状态同一性始终能完美指示血统同一性。<br />
| |
| '''k等位模型(<math display="inline">k</math> alleles model)''':突变模型中每个等位基因可以以等概率突变为其他<math display="inline">k-1</math>种可能的状态。<br />
| |
| '''逐步突变模型(Stepwise mutation model)''':突变模型中,突变产生的等位基因状态取决于该等位的初始状态。因此,状态差异越大的等位基因更可能经历了更多次历史突变事件。
| |
|
| |
| 无限等位模型未涵盖突变过程的若干特征,因此存在其他多种突变模型。显然,实际遗传位点不可能存在无限数量的可能等位。'''k等位模型'''(''<math display="inline">\pmb{k}</math> alleles model'')作为替代模型,其中<math display="inline">k</math>为表示可能等位数的有限整数。在该模型中,每个等位基因可均等概率地突变为其他<math display="inline">k-1</math>种可能状态。通过k等位模型,相同等位可能通过突变被反复创造,从而模糊了状态同一性与血统同一性的等价关系。随着可能等位数量<math display="inline">k</math>的减少和突变率的增加,等位状态作为血统同一性指标的可靠性逐渐降低,因为具有相同状态的等位基因中,具有完全独立演化历史的比例会不断上升。'''同塑性(homoplasy)'''即指具有状态同一性但缺乏血统同一性的等位基因。
| |
|
| |
| 无限等位基因模型和<math display="inline">k</math>等位基因模型都假设突变产生的新等位基因状态与当前等位基因状态无关。在这些模型中,每个等位基因突变到其他允许状态的概率相等。但突变产生的新等位基因状态也可能与原始状态相关。例如,在分化的DNA序列中常观察到转换(transition)比颠换(transversion)更普遍的现象【“transitions”译为“转换”,“transversions”译为“颠换”】。逐步突变模型(stepwise mutation model)描述了等位基因状态存在某种顺序且新状态依赖于原始状态的情况(Kimura和Ohta 1978)。微卫星或SSR位点的链滑动错配(slipped-strand mispairing)产生的突变,通常只会在原始等位基因重复次数基础上增减1或少数几次,极少出现与原始重复次数差异较大的突变。因此,微卫星位点是逐步突变的典型例子:状态相近的等位基因比差异大的等位基因更可能具有近期共同祖先。
| |
|
| |
| 突变模型的作用体现在遗传距离这一概括性指标中。Nei(1972, 1978a, b)提出的标准遗传距离<math display="inline">\mathbf{D}</math>被广泛使用。给定多个种群的等位基因频率,<math display="inline">D</math>(注意不要与配子不平衡度量混淆)表示从两个不同亚种群随机抽取的两个等位基因状态相同的概率,相对于从同一亚种群抽取的概率比值。表5.4展示了一个假设位点上两个亚种群的等位基因频率,可用于计算<math display="inline">D</math>。在随机交配下,从亚种群1抽取两个相同等位基因的总概率为:
| |
|
| |
| 表5.4 用于计算标准遗传距离<math display="inline">D</math>的两个亚种群假设等位基因频率。本例假设单个位点有三个等位基因,但适用于任意等位基因数的位点。多位点的<math display="inline">D</math>计算需使用所有位点的<math display="inline">J_{11}</math>、<math display="inline">J_{22}</math>和<math display="inline">J_{12}</math>平均值来求遗传同一性<math display="inline">I</math>。
| |
|
| |
| {|
| |
| !width="13%"| Allele
| |
| !width="28%"| Subpopulation 1
| |
| !width="15%"|
| |
| !width="28%"| Subpopulation 2
| |
| !width="15%"|
| |
| |-
| |
| |
| |
| | Frequency
| |
| | pik
| |
| | Frequency
| |
| | p
| |
| |-
| |
| | 1
| |
| | 0.60
| |
| | p²1=0.36
| |
| | 0.40
| |
| | p21=0.16
| |
| |-
| |
| | 2
| |
| | 0.30
| |
| | P²2=0.09
| |
| | 0.60
| |
| |
| |
| |-
| |
| | 3
| |
| | 0.10
| |
| | P²3=0.01
| |
| | 0.00
| |
| | P22=0.36 P23=0.00
| |
| |}
| |
|
| |
| <math display="block">
| |
| J_{11}=\sum_{k=1}^{a l l e l e s}p_{1k}^{2}=\left(0.6\right)^{2}+\left(0.3\right)^{2}+\left(0.1\right)^{2}=0.46
| |
| </math>
| |
|
| |
| 从亚种群2抽取两个相同等位基因的总概率为:
| |
|
| |
| <math display="block">
| |
| J_{22}=\sum_{k=1}^{a l l e l e s}p_{2k}^{2}=\left(0.4\right)^{2}+\left(0.6\right)^{2}+\left(0.0\right)^{2}=0.52
| |
| </math>
| |
|
| |
| 其中<math display="inline">p_{ik}</math>表示种群<math display="inline">i</math>中第<math display="inline">k</math>个等位基因的频率。从亚种群1和2各抽取一个相同等位基因的总概率为:
| |
|
| |
|
| |
| $$
| |
|
| |
| 该位点的标准化遗传同一性则为
| |
|
| |
| <math display="block">
| |
| I={\frac{J_{12}}{\sqrt{J_{11}J_{22}}}}={\frac{0.42}{\sqrt{(0.46)(0.52)}}}=0.8589
| |
| </math>
| |
|
| |
| 由此可计算遗传距离为
| |
|
| |
| <math display="block">
| |
| D=\mathrm{~-~}\ln{(I)}=\mathrm{~-~}\ln{(0.8589)}=0.152
| |
| </math>
| |
|
| |
| 当两个亚种群具有相同的等位基因频率时,<math display="inline">J_{11}</math>和<math display="inline">J_{22}</math>相等,此时<math display="inline">I</math>为1,而1的自然对数为0,遗传距离即为0。<math display="inline">D</math>没有上限。尽管这种遗传距离可计算任意种群对间的差异,但在完全隔离的种群中,若分化仅由突变引起,根据无限等位模型,<math display="inline">D</math>预期会随时间线性增加。该预期假设突变不会导致任何同塑性【homoplasy译为“同塑性”】,因此状态相同的等位基因始终具有共同血统。若不符合无限等位模型,<math display="inline">D</math>会低估真实的遗传距离,因为记录种群历史的突变事件无法在等位基因频率中完美体现。
| |
|
| |
| 遗传距离是一种旨在量化单倍型或基因型间进化事件差异的度量指标。因此,遗传距离的构建需基于描述作用过程的模型基础。例如,存在多种针对微卫星位点逐步突变模型设计的遗传距离(如 Takezaki 和 Nei 1996),而对微卫星不同遗传距离指标的比较研究发现其性能取决于突变模式(Goldstein等 1995)。类似地,一项对51个种群约900名无关个体500 000个SNP位点应用多种遗传距离的研究也发现种群划分存在显著差异(Libiger等 2009)。
| |
|
| |
| 这些比较研究强调,在使用遗传距离指标时需注意其底层突变模型及其与观测遗传数据的匹配程度。
| |
|
| |
| 在理解突变及其不同形式的基础上,我们可重新审视种群间遗传分化度量。第四章给出了亚种群相对于总种群的固定指数表达式<math display="inline">(F_{S T}=\frac{H_{T}-H_{S}}{H_{T}})</math>。该指标实际上假设了无限等位模型,因为它将所有等位基因视为具有相同突变步数差异,且所有杂合子被视为同等距离。
| |
|
| |
| Wright(1943b)已认识到突变在种群间遗传分化程度中的作用,他指出:“…只需要少量的长距离扩散或突变就能阻止大种群的分化。”在岛屿模型中,等位基因按<math display="inline">k</math>等位模型演化时,<math display="inline">F_{S T}</math>是漂变、基因流及突变影响共同作用的结果:
| |
|
| |
| <math display="block">
| |
| F_{S T}\cong\frac{1}{4N_{e}(m+\mu+\nu)}
| |
| </math>
| |
|
| |
| 其中,<math display="inline">\upmu</math> 和 <math display="inline">\nu</math> 是双等位基因位点的正向和反向突变速率。类似的正向和反向突变速率会导致等位基因频率趋向中间值,使得当突变相对于漂变较强时,亚群体表现出较低的等位基因频率分化和降低的<math display="inline">F_{ST}</math>。只有当突变速率远小于基因流速率时,<math display="inline">F_{ST}</math>才主要反映遗传漂变与基因流的净平衡关系。需注意,在无限等位基因模型下,突变会增加遗传分化,因为每个新突变都是独特的,且除非新等位基因的拷贝通过基因流在亚群体间迁移,否则仅会出现在单个亚群体中。
| |
|
| |
| 存在另一种计算固定指数的替代方法,该方法基于逐步突变模型而非无限等位基因模型,其固定指数通过下式度量:
| |
|
| |
| <math display="block">
| |
| {\hat{R}}_{ST}={\frac{S_{T}-S_{W}}{S_{T}}}
| |
| </math>
| |
|
| |
| 其中<math display="inline">S_{T}</math>是总群体中等位基因大小方差的两倍,<math display="inline">S_{W}</math>是亚群体内等位基因大小方差平均值的两倍(Slatkin 1995;Goodman 1997)。此时,等位基因的状态会影响对群体分化程度的估计。状态差异较大的等位基因(状态方差更大)在群体结构估计中被赋予更高权重,因为它们近期通过血统同一的可能性更低(需要多次逐步突变才能导致状态的显著变化)。相反,状态非常相似的等位基因(状态方差较小)对群体分化估计的贡献较小,因为它们更可能近期通过血统同一,但因突变而改变了状态。
| |
|
| |
| 使用逐步突变模型和<math display="inline">R_{ST}</math>可解释高突变速率对基因流实际发生程度的表观影响。表5.5给出了两个亚群体的假设遗传数据,展示了无限等位基因模型与逐步突变模型下群体分化程度的差异。Whitlock(2011)指出,不同群体遗传分化指标的度量对高突变速率的敏感性存在差异,并建议当突变速率相对于基因流速率较高时,采用具有明确突变模型的指标(如<math display="inline">R_{ST}</math>)更为有效。
| |
|
| |
| <span id="interact-box-5.3-r_st和boldsymbolf_st作为不同突变模型后果的示例"></span>
| |
| = Interact box 5.3 <math display="inline">R_{ST}</math>和<math display="inline">\boldsymbol{F}_{ST}</math>作为不同突变模型后果的示例 =
| |
|
| |
| 在无限等位基因模型下,等位基因状态对群体结构估计无关。然而在逐步突变模型中,等位基因状态在群体结构的总估计中被加权。通过Microsoft Excel电子表格计算两个亚群体的<math display="inline">R_{ST}</math>和<math display="inline">\boldsymbol{F}_{ST}</math>,将有助于您更好地理解突变模型如何影响对群体结构的认知。利用该电子表格探索等位基因状态差异及等位基因频率如何导致群体结构程度的差异化估计。
| |
|
| |
| 表 5.5 基于无限等位模型使用<math display="inline">\boldsymbol{F}_{S T}</math>与逐步突变模型使用<math display="inline">R_{S T}</math>的群体分化假设估计值比较。在案例1中,两个群体的大部分等位基因在状态上非常相似。在逐步突变模型下,两个等位基因之间仅相隔一次可能由突变引起的变化。因此,<math display="inline">R_{S T}</math>的估计值小于<math display="inline">\bar{F}_{S T}</math>的估计值。在案例2中,两个群体的等位基因在状态上差异较大,且根据逐步突变模型间隔超过一次突变变化。相比之下,在无限等位模型中所有等位基因仅相隔一次突变事件。<math display="inline">R_{S T}</math>的更高估计值反映了其对更大等位基因状态差异的更高权重。
| |
|
| |
| {|
| |
| !width="26%"|
| |
| !width="36%"| Case 1
| |
| !width="37%"| Case 2
| |
| |-
| |
| | Subpopulation 1 Subpopulation 2
| |
| | 9,10,10,10,10,10,10,10,10,10 12,11,11,11,11,11,11,11,11,11
| |
| | 9,10,10,10,10,10,10,10,10,10 19,20,20,20,20,20,20,20,20,20
| |
| |-
| |
| | Allele size variance in subpopulation 1, S
| |
| | 0.10
| |
| | 0.10
| |
| |-
| |
| | Allele size variance in subpopulation 2, S2
| |
| | 0.10
| |
| | 0.10
| |
| |-
| |
| | Allele size variance in total population, ST
| |
| | 0.947
| |
| | 52.821
| |
| |-
| |
| | RST
| |
| | 0.789
| |
| | 0.996
| |
| |-
| |
| | Expected heterozygosity in subpopulation 1, H
| |
| | 0.18
| |
| | 0.18
| |
| |-
| |
| | Expected heterozygosity in subpopulation 2, H2
| |
| | 0.18
| |
| | 0.18
| |
| |-
| |
| | Average subpopulation expected heterozygosity, Hs
| |
| | 0.18
| |
| | 0.18
| |
| |-
| |
| | Expected heterozygosity in total population, HT
| |
| |
| |
| |
| |
| |-
| |
| | FST
| |
| | 0.59 0.695
| |
| | 0.59 0.695
| |
| |}
| |
|
| |
| <span id="dna序列的突变模型"></span>
| |
| ==== DNA序列的突变模型 ====
| |
|
| |
| 目前广泛采用两种概念模型来描述DNA序列的突变过程(注意这些模型类型原则上也适用于氨基酸序列)。对DNA序列突变过程的一种近似是'''无限位点模型'''(infinite sites model)。每个等位基因是一个无限长的DNA序列,且每次突变发生在DNA序列的不同位置。无限位点模型可视为专门为DNA序列构建的无限等位模型。关键区别在于,无限位点模型允许突变过程在群体中每个等位基因上发生任意次数。因此,成对等位基因间的进化”距离”可以存在差异——根据每个等位基因经历的突变次数,成对等位基因间可能有少量或大量位点差异。图5.10A展示了无限位点模型下DNA序列可能发生的突变示例。例如,当序列1的第4个碱基对位点从G突变为C后,该位点不会再发生其他突变。因此,在序列比对中所有发生突变的位点均可被区分,因为每个位点仅经历一次突变。尽管遗传漂变和自然选择等其他过程可能影响序列频率,但我们可以得出:在某个位点共享相同碱基的序列具有同源性。
| |
|
| |
| 尽管没有DNA序列是无限长的,但若没有经过太长时间使得序列共享一个共同祖先,无限位点模型仍是一个合理的近似。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/0e69042fd77aec8e1a36003b865e34f4af67644a7272fa9fb01b88f19c620100.jpg]]<br />
| |
| 图5.10 无限位点(a)和有限位点(b)模型下DNA序列的突变模式。由突变产生的碱基对状态以小写字母表示,若突变发生一次则标记为红色阴影,若发生两次则标记为蓝色阴影。在无限位点模型中,同一站点状态相同的序列因血统同一性而相同,因为每个站点仅发生一次突变。相比之下,有限位点模型展示了同一站点多次突变如何模糊基于DNA序列站点差异比较的血统同一性历史。顶部面板中包围序列的省略号(…)表示每条序列有无限多个站点,仅显示其中10个。
| |
|
| |
| <span id="专栏5.1-单核苷酸多态性"></span>
| |
| = 专栏5.1 单核苷酸多态性 =
| |
|
| |
| DNA测序现已成为广泛用于确定单倍型【“haplotypes”译为“单倍型”】和基因型的分子技术。图5.11展示了来自四个个体的假设DNA序列集。每行代表一个个体DNA序列的某一段,每列代表一个血统同一(即同源)的核苷酸位点。通过比较每个个体在某一站点的核苷酸碱基状态,可检测个体间的核苷酸变异。
| |
|
| |
| 若被测序个体属于同一物种,则变异的核苷酸位点称为单核苷酸多态性(SNPs,发音为“snips”)。DNA序列在每个核苷酸位点最多呈现<math display="inline">k=4</math>种等位基因,因此突变模式和速率需用特殊的<math display="inline">k</math>等位模型描述。
| |
|
| |
| 若被测序个体属于不同物种,则变异的核苷酸位点被描述为序列分歧。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/148625a5cf6bcca1be27a29b54c474446677bd95a91d5e3006d30f011c36d873.jpg]]<br />
| |
| 图5.11 四个个体在某一基因座的假设DNA序列及多序列比对结果,标识出多态性核苷酸位点(阴影标记并带有星号)。
| |
|
| |
| 若突变随机发生且在各个位点概率相等,则单个位点经历两次突变的概率极低(例如每站点突变率的平方值很小)。在相对较短的时间内(如数千代),仅有少量突变可能发生,因此同一位点发生多次突变的可能性极低。
| |
|
| |
| 然而,实际的DNA序列是有限的,且发生突变的时间跨度可能非常长,因此需要考虑这些事实的突变模型更为实用。'''有限位点模型'''(''finite sites model'')适用于长度有限的DNA序列。它与'''无限位点模型'''(''infinite sites model'')类似,但不同之处在于位点数量有限且每个位点可能经历多次突变。如图5.8B所示,多次突变可能掩盖过去的突变事件。例如,两条序列在每个位点要么相同要么不同,但差异位点可能在历史上发生过多次突变。序列1的第四个位点就是这种情况:尽管该位点发生了两次突变,但第二次突变导致核苷酸恢复到最初的状态。然而,在所有三条序列的比对中,第四个位点显示为完全一致,无法检测到序列1在该位点发生的两次突变事件。类似的情况也出现在序列3的第七位点。当比较序列对时,序列2和序列3在四个位点(1、7、8和10)存在差异,但实际上历史上有五次突变事件将它们区分开。序列1和序列3在三个位点(4、7和10)存在差异,但实际上经历了五次突变事件。因此,同一位点的多次突变会掩盖区分DNA序列的突变事件完整历史。
| |
|
| |
| '''无限位点模型'''(''infinite sites model''):假设DNA序列无限长,每个突变发生在不同位点,且同一位置不会经历多次突变的模型。<br />
| |
| '''有限位点模型'''(''finite sites model''):适用于有限长度DNA序列的突变模型,允许同一位点发生多次突变。
| |
|
| |
| 同一位点可能发生多次突变(常称为'''多次命中''',''multiple hits'')的现象,会随时间推移导致突变变化的饱和——即同一位置反复发生突变。这种饱和可通过核苷酸替代模型进行“校正”,这类模型通过估计并调整同一位置的多次突变,来计算两条序列间真实的突变事件数量。第8章将介绍一种称为'''Jukes–Cantor模型'''的校正方法。
| |
|
| |
| 理解多次命中影响的一种方式,可类比第3章中装有微量离心管的烧杯实验。假设烧杯中含有大量等比例(各25%)的核苷酸(A、C、T、G)。通过从烧杯中随机抽取核苷酸构建两条DNA序列时,某个核苷酸被随机选中的概率为<math display="inline">25\%</math>。因此,给定一条随机DNA序列,另一条随机序列在相同位点拥有相同碱基对的概率为<math display="inline">25\%</math>。这意味着,即使同一位置经历了多次突变,两条DNA序列仍可能在该位点保持25%的碱基对一致性。因此,当存在多次命中的可能性时,'''状态一致'''(''identity in state'')并不能完全反映'''血统一致'''(''identity by descent'')。
| |
|
| |
| <span id="突变对等位基因频率与自合性autozygosity的影响"></span>
| |
| ==== 5.4 突变对等位基因频率与自合性(autozygosity)的影响 ====
| |
|
| |
| 不可逆与双向突变模型。突变与基因流动过程之间的相似性。突变与遗传漂变下平衡时的预期自合性。预期杂合度与<math display="inline">\theta</math>的生物学解释【“biological interpretation”译为“生物学解释”】。
| |
|
| |
| 在迄今建立的等位基因与基因型频率预期中,所有过程仅作用于塑造现有遗传变异。要理解突变的后果,需要能预测在持续突变输入遗传变异条件下的等位基因与基因型模型。本节提出三个突变过程模型。前两个模型相互关联,探讨复发性突变如何随时间改变群体中的等位基因频率。第三个模型预测当遗传漂变与突变共同作用时的基因型频率,展示这些过程的组合如何影响群体中的自合性。
| |
|
| |
| 让我们建立两个简单模型来预测持续突变对单一极大规模随机交配群体中等位基因频率的影响(有时称为突变压力)。两个模型将仅聚焦于突变过程,忽略遗传漂变或自然选择等其他过程。考虑一个具有两个等位基因A和a的位点,其中A的频率用<math display="inline">p</math>表示,a的频率用<math display="inline">q</math>表示。对于第一个模型,假设突变仅将A等位基因转化为a等位基因,而a等位基因不能突变为A等位基因。这称为不可逆突变或单向突变模型。每个A等位基因每代发生状态改变的概率用<math display="inline">\mu</math>(发音”mu”)表示。经过一代突变后的A等位基因频率为:
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/661f90e94b1b1bf874e6555f8750ce455088518d80794285f99198ee2f46928c.jpg]]<br />
| |
| 图5.12 五种初始等位基因频率下,双等位基因位点因不可逆或单向突变导致的预期等位基因频率变化。此处A等位基因突变为a等位基因的概率(或每座位突变率)为0.00001。相比每座位突变率估计值(见表5.1),此突变率较高。预期平衡等位基因频率为<math display="inline">p=0</math>,因为群体中不存在补充A等位基因的过程。即使经过100 000代演化,群体仍未达到平衡。仅由突变引起的等位基因频率变化发生在极长的时间尺度上。
| |
|
| |
| <math display="block">
| |
| p_{t+1}=p_{t}(1-\mu)
| |
| </math>
| |
|
| |
| 其中<math display="inline">(1-\mu)</math>项表示在时间<math display="inline">t</math>未突变为a等位基因的A等位基因比例。只要<math display="inline">\mu</math>不为0,则A等位基因频率将随时间下降,因为<math display="inline">1-\mu</math>小于1。这也意味着a等位基因的比例每代增加<math display="inline">\mu</math>。若突变率随时间保持恒定,则经过任意代数后的等位基因频率为:
| |
|
| |
| <math display="block">
| |
| p_{t}=p_{0}(1-\mu)^{t}
| |
| </math>
| |
|
| |
| 其中<math display="inline">p_{0}</math>为初始等位基因频率,<math display="inline">t</math>为经过的世代数。
| |
|
| |
| 在不可逆突变的情况下,由于种群中不存在替换''A''等位的机制,最终所有''A''等位都将通过突变为转化为''a''等位。图5.12展示了当突变率<math display="inline">\mu=1\times{10}^{-5}</math>(即0.00001)时,五种不同初始等位频率下''A''等位频率随时间变化的预期趋势。值得注意的是,降低''A''等位频率所需的时间尺度非常漫长。在此例中,即使经过100000代,等位频率仍未达到平衡态<math display="inline">p=0</math>。实际上,在如此高的突变率(表5.1所列观测范围上限)下,仍需69310代才能使''A''等位频率减半(通过设定<math display="inline">\left(1-\upmu\right)^{\mathrm{t}}=0.5</math>计算半衰期)。从不可逆突变模型可以推断,突变过程确实会影响等位频率,但仅通过突变引起等位频率的显著变化需要数千至上万代,具体取决于突变率。
| |
|
| |
| '''不可逆或单向突变''':在双等位基因位点中,''A''等位突变为''a''等位但无反向突变的过程。<br />
| |
| '''突变压力''':种群中持续发生改变等位状态的突变。<br />
| |
| '''可逆或双向突变''':在双等位基因位点中,''A''等位与''a''等位之间可相互转化的突变过程。
| |
|
| |
| 不可逆突变的假设在生物学上并不现实。突变通常能改变所有等位的状态,导致双等位基因位点同时发生正向(<math display="inline">\mathrm{A\to a}</math>)和逆向(<math display="inline">\mathrm{a\to A}</math>)突变。双向或可逆突变模型通过引入独立的正向突变率(<math display="inline">\mu</math>)和逆向突变率(<math display="inline">\nu</math>,读作”nu”)来考虑这种情况。在双向突变压力作用下,我们可以重新探讨突变如何随时间改变种群中的等位频率。每一代中,<math display="inline">\mu</math>比例的''A''等位会突变为''a''等位,同时<math display="inline">\nu</math>比例的''a''等位会突变为''A''等位。因此,经过一代后的等位频率为:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=p_{t}(1-\mu)+(1-p_{t})\nu
| |
| </math>
| |
|
| |
| 其中,''A''等位频率的减少源于经历正向突变的等位比例(<math display="inline">p_{t}(1-\mu)</math>),而其增加则源于经历逆向突变的等位比例(<math display="inline">(1-p_{t})\nu</math>)。总体而言,''A''等位的平衡频率由两种突变率的净平衡决定:
| |
|
| |
| <math display="block">
| |
| p_{equilibrium}=\frac{\upnu}{\mu+\upnu}
| |
| </math>
| |
|
| |
| 如数学框5.1所示。因此,无论A等位基因的初始频率如何,种群都将收敛到<math display="inline">p_{equilibrium}</math>,这个平衡点更接近于由两个突变率中较高者产生的等位基因。图5.13展示了在双向突变下,五种不同初始等位基因频率时A等位基因随时间变化的频率。由于图中使用的前向和后向突变率不相等但差异在五倍以内,两种等位基因在平衡时都具有中等频率。达到平衡等位基因频率所需的世代数再次非常漫长,这与不可逆突变模型的情况相同。
| |
|
| |
| <span id="数学框5.1-双向突变下的平衡等位基因频率"></span>
| |
| = 数学框5.1 双向突变下的平衡等位基因频率 =
| |
|
| |
| 为确定具有双向突变可能性的双等位基因位点的平衡等位基因频率,我们采用预测一代内等位基因频率变化的基本方程:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=p_{t}(1-\mu)+\big(1-p_{t}\big)\nu
| |
| </math>
| |
|
| |
| 并将其重表达为:
| |
|
| |
| <math display="block">
| |
| p_{t+1}-a=\left(p_{t}-a\right)b
| |
| </math>
| |
|
| |
| 其中<math display="inline">a</math>和<math display="inline">b</math>是仅取决于前向突变率<math display="inline">\mu</math>和后向突变率<math display="inline">\nu</math>的常数。通过这种形式表达方程,当<math display="inline">(p_{t}-a)b</math>项在特定极限条件下趋近于0时,我们可以将<math display="inline">p_{t+1}</math>等同于<math display="inline">a</math>。将方程5.25重新排列,两边加<math display="inline">a</math>:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=(p_{t}-a)b+a
| |
| </math>
| |
|
| |
| 展开后得到:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=p_{t}b-a b+a
| |
| </math>
| |
|
| |
| 最后提取<math display="inline">a</math>的因子项:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=p_{t}b+a(1-b)
| |
| </math>
| |
|
| |
| 将包含突变率的方程5.24展开为相同形式:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=p_{t}-p_{t}\mu+\nu-p_{t}\nu
| |
| </math>
| |
|
| |
| 提取公因子后得到:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=p_{t}\mathopen{}\mathclose\bgroup\left(1-\mu-\nu\aftergroup\egroup\right)+\nu
| |
| </math>
| |
|
| |
| 比较方程5.28和5.30可得:
| |
|
| |
| <math display="block">
| |
| b=\left(1-\mu-\nu\right)
| |
| </math>
| |
|
| |
| 以及:
| |
|
| |
| <math display="block">
| |
| a(1-b)=\nu
| |
| </math>
| |
|
| |
| 将<math display="inline">b</math>的表达式代入上式即可解得<math display="inline">a</math>:
| |
|
| |
| <math display="block">
| |
| a=\frac{\nu}{\mu+\nu}
| |
| </math>
| |
|
| |
| 将这些<math display="inline">a</math>和<math display="inline">b</math>的值代入方程5.25,得到等位基因频率单代变化的新表达式:
| |
|
| |
| <math display="block">
| |
| p_{t+1}-\frac{\nu}{\mu+\nu}=\left(p_{t}-\frac{\nu}{\mu+\nu}\right)\left(1-\mu-\nu\right)
| |
| </math>
| |
|
| |
| 由于任何一代间隔内的等位基因频率变化表达式都相同,且突变率随时间恒定,我们可以用初始等位基因频率<math display="inline">p_{0}</math>和经过的世代数<math display="inline">t</math>来重写该方程:
| |
|
| |
| <math display="block">
| |
| p_{t+1}-\frac{\nu}{\mu+\nu}=\left(p_{0}-\frac{\nu}{\mu+\nu}\right)\left(1-\mu-\nu\right)^{t}
| |
| </math>
| |
|
| |
| 注意当世代数极大时<math display="inline">\left(t\rightarrow\infty\right)</math>,<math display="inline">(1-\mu-\nu)^{t}</math>项趋近于0,使得方程右侧整体为零。因此,当经过多代后,平衡等位基因频率应为:
| |
|
| |
| <math display="block">
| |
| p_{t\rightarrow\infty}=\frac{\nu}{\mu+\nu}
| |
| </math>
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/24574eafc85366a0107ce454df2d2d35d50b2b46a0c2955d9138177e9cd4c0a2.jpg]]
| |
|
| |
| 图 5.13 在双等位基因位点上,由于可逆或双向突变导致的等位基因频率预期变化,展示了五种初始等位基因频率的情况。此处,A等位基因突变为a等位基<math display="inline">\mathrm{(A\toa)}</math>的概率为0.0001,而a等位基因突变为A等位基<math display="inline">(\mathbf{a}\longrightarrow\mathbf{A})</math>的概率为0.00005。这些突变率处于估计突变率范围的高值端(见表5.1)。根据方程5.22,预期平衡值为<math display="inline">p=0.333</math>,这一等位基因频率需经历数万代才能达到。达到平衡的时间与突变率的绝对大小成正比,而平衡值仅取决于突变率比值的函数关系。
| |
|
| |
| 图 4.7. 此处,两条曲线的形态同样完全一致,且两种过程在平衡时均导致等位基因频率处于中间值。突变与基因流图表的主要差异体现在时间尺度上。若无其他过程干扰,基因流可使等位基因频率在数十至数百代内趋近平衡值,而突变则需数万至数十万代才能使等位基因频率接近平衡。需理解,这种时间尺度的差异源于两种过程的速率差异极大,而非
| |
|
| |
| 结果表明,群体内的突变过程与多个亚群体间的基因流过程完全可比。对比图5.12(不可逆突变)与图4.6(大陆-岛屿模型中单向基因流下的等位基因频率),二者均导致等位基因频率朝向固定与丢失状态变化,且曲线形态一致。接着,对比图5.13的双向突变过程与
| |
|
| |
| <span id="互动框-5.4-模拟不可逆与双向突变"></span>
| |
| === 互动框 5.4 模拟不可逆与双向突变 ===
| |
|
| |
| 访问教材网站以模拟不可逆与双向突变模型。
| |
|
| |
| 首先运行模拟:2000代,<math display="inline">N_{e}=20</math>,初始等位基因频率0.9且无突变,观察仅由遗传漂变产生的模式。随后勾选突变选项,设定正向突变率为0.01、逆向突变率为零(不可逆模型中某一突变率为零),初始等位基因频率0.9,模拟2000代。同时模拟正向突变率0.001的情况。比较有突变与无突变时重复位点的等位基因频率分布。当正向突变率为0.01和0.001时,趋近平衡的速度如何?
| |
|
| |
| 对于双向模型,比较2000代内当正逆向突变率相等(如均为0.01)与不等(如0.01和0.005)时从初始等位基因频率0.5趋近平衡的过程。模拟结果与双向突变的预期平衡等位基因频率如何对应?
| |
|
| |
| 需注意,这些突变率仅为示例,生物学现实的突变率通常远低于此值。
| |
|
| |
| 在过程本身存在根本性差异。图中,配子迁移的概率为十分之一,而等位基因突变的概率在千分之一到万分之一之间。虽然这些速率可能处于自然种群中发现值的较高端,但一般而言,基因流的预期发生速率远高于突变。通过这一比较得出的结论是:在短期内,基因流是比突变更强大的改变单一位点等位基因频率的力量。突变确实有效应,但其作用是长期的。
| |
|
| |
| 基因流与突变过程的平行性可被用作优势来进一步理解突变过程。特别是,我们可以在基因漂变也起作用的有限种群中更深入地了解突变如何影响自合性。回顾第3章中由遗传漂变引起的有限种群自合性水平的表达式:
| |
|
| |
| <math display="block">
| |
| F_{t}=\frac{1}{2N_{e}}+\biggl(1-\frac{1}{2N_{e}}\biggr)F_{t-1}
| |
| </math>
| |
|
| |
| <math display="inline">\left(1-\mu\right)^{2}</math>、<math display="inline">2\mu(1-\mu)</math>和<math display="inline">\mu^{2}</math>。只有不含突变等位的<math display="inline">\left(1-\mu\right)^{2}</math>基因型能对可能因有限取样而成为同源遗传的等位池作出贡献。从相反视角看,注意每代预期会出现<math display="inline">2\mu(1{-}\mu)</math>杂合基因型和<math display="inline">\mu^{2}</math>纯合新突变基因型。这两类含突变的基因型共同将自合性降低<math display="inline">1-2\mu(1-\mu){-}\mu^{2}=(1-\mu)^{2}</math>倍。(这与第4章中关于基因流的推理完全相同。)
| |
|
| |
| 因此,突变将通过<math display="inline">\left(1-\mu\right)^{2}</math>因子减少当前世代有限取样导致的自合性(概率为<math display="inline">\frac{1}{2N_{e}}</math>)。此外,突变还将减少来自过去世代的自合性<math display="inline">(F_{t-1})</math>,因为部分同源等位可能通过突变变为新状态,仅保留<math display="inline">\left(1-\mu\right)^{2}</math>比例的基因型不受突变影响并维持原有自合水平。将这两项自合性调整合并可得:
| |
|
| |
| 突变通过改变等位状态打破遗传链条,从而降低基因型由两个同源等位(自合)组成的概率。每代不含、含一个或两个突变等位的基因型频率分别为:
| |
|
| |
| <math display="block">
| |
| F_{t}=\frac{1}{2N_{e}}\left(1-\mu\right)^{2}+\left(1-\frac{1}{2N_{e}}\right)\left(1-\mu\right)^{2}F_{t-1}
| |
| </math>
| |
|
| |
| 假设突变率极小且远低于有效种群大小(参见数学框4.1中关于基因流的推导),在经历突变的有限种群中,平衡状态下预期自合性的近似值为:
| |
|
| |
| <math display="block">
| |
| F_{e q u i l i b r i u m}\cong\frac{1}{4N_{e}u+1}
| |
| </math>
| |
|
| |
| 该结果还依赖于每次突变产生种群中不存在的新等位(即无限等位模型)。由于预期杂合性的异合性仅为1减去自合性,
| |
|
| |
| $$
| |
|
| |
|
| |
| $$
| |
|
| |
| 这是有限种群中预期的杂合度,此时遗传漂变推动等位基因频率向固定和丢失的”推力”与突变推动等位基因频率远离固定和丢失的”推力”达到了动态平衡。
| |
|
| |
| 当<math display="inline">N_{e}</math>较大且<math display="inline">\mu</math>较小时,量<math display="inline">4N_{e}\mu</math>具有直接的生物学解释。在由<math display="inline">2N_{e}</math>个等位基因组成的种群中,每代发生突变的等位基因期望数量为<math display="inline">2N_{e}\mu</math>。在组成二倍体基因型的两个等位基因样本中,任一等位基因发生突变(因此不具有共同血统)的概率为<math display="inline">2(2N_{e}\mu)=4N_{e}\mu</math>。例如,在<math display="inline">2N_{e}=100</math>的种群中,等位基因每代的突变率为万分之一(<math display="inline">\mu=0.0001</math>),则突变的期望数量为0.01,样本中包含两个非自合(autozygous)等位基因的概率为0.02。量<math display="inline">4N_{e}\mu</math>常被符号化为<math display="inline">\theta</math>(读作”theta”)。在无限等位模型下,<math display="inline">\theta</math>表示从漂变-突变平衡种群中随机取样的两个等位基因形成异合(allozygous)对的概率。当<math display="inline">\theta=0.02</math>时,漂变-突变平衡下的期望杂合度为0.0099。值得注意的是,若不满足无限等位或无限位点模型,平衡杂合度将低于<math display="inline">\theta</math>的预测值。这是因为在有限等位状态下,并非所有突变事件都会产生新的等位基因:当与种群中现有等位基因共同取样时,有些突变无法形成异合对或杂合体。实际上,产生现有等位基因额外拷贝的突变会通过同塑性(homoplasy)增加表观纯合度。
| |
|
| |
| 图5.14展示了突变-遗传漂变平衡下自合性与异合性的期望概率。当<math display="inline">4N_{e}\mu</math>较小时,由于突变引入新等位基因与遗传漂变推动等位基因频率向固定/丢失的平衡作用,自合性会维持在中等平衡水平。当<math display="inline">4N_{e}\mu</math>增大时,微弱漂变或高频突变将导致几乎完全的杂合性(无自合性)。反之,<math display="inline">4N_{e}\mu</math>趋近零表明强漂变或低频突变,导致高自合性和低杂合性。需要注意的是,达到预期的平衡自合性或杂合性水平需要经过<math display="inline">4N_{e}</math>代的时间尺度。
| |
|
| |
| <span id="互动框5.5-双向突变下的杂合度与纯合度"></span>
| |
| = 互动框5.5 双向突变下的杂合度与纯合度 =
| |
|
| |
| 使用文本模拟网站观察双向突变与遗传漂变如何影响纯合度与杂合度。重点关注右侧显示多个重复位点等位基因频率集合分布的图表。
| |
|
| |
| 首先运行模拟500代,<math display="inline">N_{e}=20</math>,初始等位基因频率为0.5且无突变,观察仅由遗传漂变产生的模式。有多少位点表现出完全纯合性或部分杂合性?接着勾选突变选项,将正向和反向突变率设为0.01。此时<math display="inline">\theta=4N_{e}\mu</math>的值是多少?突变如何影响等位基因频率的集合分布,进而影响具有某种杂合性水平的位点数量?再模拟突变率为0.001的情况,计算<math display="inline">\theta=4N_{e}\mu</math>的值。相较于低突变率,高突变率下观察到的杂合性水平有何差异?
| |
|
| |
| 该模拟的突变模型与<math display="inline">\theta=4N_{e}\mu</math>的突变模型假设有何不同?这对突变维持的杂合性水平有何影响?
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/e4114f00d754238f8265e293a8d334b44371a36d11fab436cda6f23766b91d8c.jpg]]<br />
| |
| 图5.14 在遗传漂变和突变共同作用的群体中,平衡状态下预期的纯合性(autozygosity,实线)和杂合性(allozygosity,虚线)。随机从群体中取样的两个等位基因状态相同的概率,取决于遗传漂变(推动群体中单一等位基因固定)与突变(将现有等位基因转变为新状态)之间的动态平衡。关键假设是无限等位模型,该模型保证每次突变都产生独特等位基因,从而最大化由突变引起的allozygosity。
| |
|
| |
| 由于突变率极低,突变过程极为缓慢,因此恢复突变-漂变平衡需要经历极多世代。若杂合性偏离其突变-漂变平衡点,群体将需要极长时间才能恢复至该平衡。
| |
|
| |
| <span id="包含突变的溯祖模型"></span>
| |
| ==== 5.5 包含突变的溯祖模型 ====
| |
|
| |
| 在溯祖过程中加入突变机制:<br />
| |
| 较长的谱系分支会积累更多突变<br />
| |
| 基于无限等位模型和无限位点突变模型的谱系结构
| |
|
| |
| <pre class="markdown">谱系分支模型在第3章中针对单一有限种群被引入,随后在第4章扩展以解释种群细分下预期的分支模式。这些章节的目标是预测谱系分支模式,而不涉及由分支所代表的谱系身份。这些分支模型需要进一步扩展以考虑发生突变的可能性。突变会改变由谱系树中的每个谱系或分支代表的基因或DNA序列。因此,考虑突变将是发展溯祖模型以解释当前样本谱系间差异的关键步骤。本节将重点关注溯祖模型中突变的作用以及谱系树中各谱系的状态。这通过将合并过程与突变过程在时间回溯至最近共同祖先的过程中耦合来实现。最终目标是建立一个谱系分支模型,用于预测从实际种群中采集的谱系样本可能预期的等位基因数量和类型。例如,一个预测可能是在给定突变率下单一有限种群中预期的等位基因数量。通过这种方式,合并过程与突变过程的结合被用于形成对由不同种群遗传过程产生的遗传变异模式的定量预期。
| |
|
| |
| 构建包含突变的溯祖模型非常简单,只需添加另一种可能在现在与过去某个时间之间发生的事件类型(图5.15)。我们将假设合并事件与突变事件均罕见(或$N_{e}$较大且突变率较小),因此当事件在时间回溯中发生时,要么是合并要么是突变。换句话说,我们假设突变事件与合并事件是互斥的。
| |
|
| |
| 
| |
| 图5.15 合并事件与突变事件背景下的单倍体繁殖。在单倍体种群中,合并概率为$\frac{1}{2N}$(实线),而两个谱系在前一代没有共同祖先的概率为$1-\frac{1}{2N}$(虚线)。突变过程也可能同时发生(星号),改变等位基因的状态(实心圆变为空心圆)。
| |
|
| |
| 每一代都存在发生突变的可能性。突变率$\mu$可理解为每个谱系每代经历突变的概率。因此,一个谱系未经历突变的概率为每代$1-\mu$。在$t$代后首次发生突变事件的概率是$t-1$代无突变后接一次突变的概率乘积,即:
| |
|
| |
| $$
| |
| P(T_{\text{mutation}}=t)=(1-\mu)^{t-1}\mu
| |
| $$</pre>
| |
| 该方程的形式与第3章中给出的经过<math display="inline">t</math>代后发生溯祖事件(coalescent event)的概率完全相同。与溯祖概率类似,随时间发生突变的概率也是一个几何级数(geometric series),可用指数分布(exponential distribution)近似(见数学框3.2)。
| |
|
| |
| 为了得到描述突变事件频率的指数表达式或<math display="inline">e</math>的指数,我们需要确定突变发生的预期速率。当时间以连续尺度<math display="inline">t=\frac{j}{2N_{e}}</math>衡量时,一个时间单位相当于<math display="inline">2N_{e}</math>代。若经过<math display="inline">2N_{e}</math>代且每代突变率为<math display="inline">\mu</math>,则在连续时间的一个单位内预期会发生<math display="inline">2N_{e}\mu</math>次突变。若定义<math display="inline">\theta=4N_{e}\mu</math>,则<math display="inline">\theta/2</math>等于<math display="inline">2N_{e}\mu</math>。由此可得单个谱系在第<math display="inline">t</math>代发生突变的指数近似概率:
| |
|
| |
| 类似逻辑)。在连续时间框架下,<math display="inline">k</math>个谱系中任意一个在时间<math display="inline">t</math>或之前发生突变的概率可用累积指数分布近似:
| |
|
| |
| <math display="block">
| |
| P(T_{m u t a t i o n}\leq t)=1-e^{-t\frac{\theta}{2}k}
| |
| </math>
| |
|
| |
| 这与溯祖事件时间近似的方法完全一致。
| |
|
| |
| 当两个独立过程同时作用时,溯祖模型变为沿时间回溯谱系并等待事件发生的模型。可能的事件包括突变或溯祖,因此任何事件发生的总概率是两类互斥事件独立概率之和。随着时间回溯(<math display="inline">t</math>增加),事件发生的总概率为:
| |
|
| |
| <math display="block">
| |
| P(T_{e v e n t}\leq t)=1-e^{-t\frac{k\left(k-1+\theta\right)}{2}}
| |
| </math>
| |
|
| |
| 其中<math display="inline">e</math>的指数为<math display="inline">-t\left[k{\frac{\theta}{2}}+{\frac{k(k-1)}{2}}\right]</math>,即突变和溯祖强度的总和。当事件确实按此指数分布的时间发生时,需判断该事件是溯祖还是突变。事件为突变或溯祖的总强度为<math display="inline">{\frac{k\theta}{2}}+{\frac{k(k-1)}{2}}</math>。因此,事件为突变的概率为:
| |
|
| |
| <math display="block">
| |
| P(T_{m u t a t i o n}=t)=e^{-t\frac{\theta}{2}}
| |
| </math>
| |
|
| |
| 在连续时间尺度下。当存在多个谱系时,每个谱系有独立概率发生突变,但每次只能有一个谱系发生突变。当事件独立但互斥时,所有可能事件的概率相加即得事件发生的总概率。将所有<math display="inline">k</math>个谱系的突变概率<math display="inline">e^{-t\frac{\theta}{2}}</math>相加,可得突变总概率:
| |
|
| |
| <math display="block">
| |
| P(T_{m u t a t i o n}=t)=e^{-t\frac{\theta}{2}k}
| |
| </math>
| |
|
| |
| 对于<math display="inline">k</math>个谱系(将此式与<math display="inline">k</math>个谱系在时间<math display="inline">t</math>的溯祖概率<math display="inline">e^{-t\frac{k(k-1)}{2}}</math>比较)。基于:
| |
|
| |
| <math display="block">
| |
| {\frac{\frac{k\theta}{2}}{{\frac{k\theta}{2}}+{\frac{k(k-1)}{2}}}}={\frac{\theta}{k-1+\theta}}
| |
| </math>
| |
|
| |
| 而事件为溯祖的概率为:
| |
|
| |
| <math display="block">
| |
| {\frac{\frac{k(k-1)}{2}}{{\frac{k\theta}{2}}+{\frac{k(k-1)}{2}}}}={\frac{k-1}{k-1+\theta}}
| |
| </math>
| |
|
| |
| 使用由方程5.45指定的累积指数分布,并通过判断每个事件是突变还是溯祖,可以构建一个包含各分支上突变可能性的溯祖谱系(图5.16)。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/a9f778ecce26087aadc5b3b4550ec76a9170f86ecbcadcb77b008120f51ce4d9.jpg]]<br />
| |
| 图5.16 在有限种群内溯祖过程与突变过程同时作用下构建的谱系。从现在向过去回溯时,突变和溯祖事件都可能发生。蓝点代表随机分配到现存谱系的突变事件。突变事件会改变谱系状态,使其与所有现存谱系最近共同祖先的原始状态产生分歧。
| |
|
| |
| 谱系树上的突变模式具有某些普遍特征。由于假设突变概率随时间恒定不变,时间越长发生突变的可能性越大。这意味着在溯祖树中,较长分支平均会经历更多突变,而较短分支出现突变的概率较低。回忆第三章中关于分支长度作为”道路”的隐喻:若将突变视为公路上按单位距离恒定概率出现的路标,则较长路段预期会有更多路标。将此逻辑应用于图5.16这类谱系可知,在两条谱系(k=2)的较长平均等待时间内,预期发生的突变会比六条可溯祖谱系(k=6)时期更多。另一个例子是不同迁移水平下两个种群谱系的预期突变模式(见图4.17)。当迁移极为有限时,在各种群内部单条谱系溯祖之前的长分支上预期会发生多次突变;而高迁移率时突变数量将显著减少。
| |
|
| |
| <span id="互动框5.6-构建含突变的溯祖谱系"></span>
| |
| = 互动框5.6 构建含突变的溯祖谱系 =
| |
|
| |
| 通过构建若干溯祖树,可以帮助理解突变与溯祖过程共同作用下的谱系演化。可使用第三章构建溯祖树时所用Microsoft Excel电子表格的扩展版本,该版本现在可模拟突变和溯祖的等待时间。该表格包含用于确定最多六条谱系的溯祖或突变事件发生时间的累积指数分布(见方程5.45)。对于给定谱系数k和突变率,通过选取0到1之间的随机数并与累积指数分布比对,可确定事件发生时间。与随机数匹配的分布时间间隔即为事件时间。下一步通过将随机数与各类事件发生概率(方程5.46和5.47)比对,确定事件类型是突变还是溯祖。
| |
|
| |
| 步骤1:打开电子表格,点击单元格查看使用的公式,尤其是每个<math display="inline">k</math>的累积'''溯祖概率'''(cumulative probability of coalescence)。这将帮助你理解本章节中的方程式如何应用于实践。你可以比较绘制的<math display="inline">k=6</math>和<math display="inline">k=2</math>的累积概率分布图。<br />
| |
| 步骤2:查看表格右侧标题为“事件时间:”(Event times:)的部分。该部分给出了事件发生前的等待时间,并确定事件是溯祖还是突变。按下重新计算键以生成新的随机数集(如有需要请参考Excel帮助文档)。观察事件时间的变化。<br />
| |
| 步骤3:现在,绘制一个可能包含突变的谱系树(在完成步骤6前不要再次重新计算)。在一张空白纸的底部画六个等距的点,代表六个谱系。<br />
| |
| 步骤4:从第一个“确定事件时间:”(Decide event time:)面板开始,确定直到发生突变或溯祖事件的时间量(向回溯时间)。然后,使用“确定事件类型:”(Decide what type of event:)下方的条目判断事件是溯祖还是突变。若为突变,转至步骤5;否则转至步骤6。<br />
| |
| 步骤5:若事件为突变,将所有谱系的线条按等待时间的长度向后绘制(例如时间为0.5时,绘制<math display="inline">0.5\mathrm{cm}</math>长的线条)。使用随机数表选择一个谱系,并在事件时间处对该谱系标记X以表示发生突变。若发生突变,谱系数量<math display="inline">(k)</math>保持不变。移至下一个“确定事件时间:”面板,获取同一<math display="inline">k</math>值的下一个事件时间。重复步骤5直至事件为溯祖事件。<br />
| |
| 步骤6:使用随机数表选择两个将发生溯祖的谱系。用这些谱系编号标注最左侧的两个点。然后用尺子从上次事件结束处开始,绘制两条平行垂直线,其长度等于连续时间中的溯祖时间(例如时间为0.5时,绘制<math display="inline">0.5\mathrm{cm}</math>长的线条)。用水平线连接这两条垂直线。将其中一个合并谱系的编号赋予水平线处的共同祖先节点。将另一个谱系编号记录到“种群中已消失谱系”列表中(若这些编号再次出现在随机数表中则跳过)。此时剩余<math display="inline">k-1</math>个谱系。
| |
|
| |
| 步骤7:返回步骤4直至所有谱系完成溯祖(<math display="inline">k=1</math>)。
| |
|
| |
| 你将得到一棵如图5.16所示的带有分支突变的溯祖树。由于随机溯祖和突变时间围绕其平均值波动,你的树会有所不同,但整体形态(例如<math display="inline">k</math>较大时分支较短)和突变频率(给定突变率下)将相似。
| |
|
| |
| 在前一种情况下,突变导致两个'''繁育群'''(demes)间的谱系显著分化,而在后一种情况下,不同繁育群中的谱系积累差异的机会较少。
| |
|
| |
| 像图5.16所示带有基因突变的系谱图,在与突变模型结合之前都是抽象化的。图5.17展示了同一系谱图在以下假设下的情况:最近共同祖先(MRCA)具有等位状态A,且突变变化遵循无限等位模型。每个突变事件都是谱系当前状态转变为种群中尚未存在的等位状态的实例。由于祖先等位状态的突变变化,现存的六个谱系代表了四种等位状态。其中两个等位的频率为<math display="inline">2/6=33\%</math>,而剩余两个等位的频率为<math display="inline">1/6=16.6\%</math>。具有B和C等位的谱系在状态上完全相同,因此可视为血统相同。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/df4409bc98adb202d4b0776e0cff73782c533db3b5e56ae19f31028683323230.jpg]]<br />
| |
| 图5.17 在单一有限种群中溯祖与突变同时发生过程下构建的系谱图。此处假设突变的无限等位模型以确定系谱图中各谱系的等位状态。通过任意指定最近共同祖先的等位状态为A,每个突变事件将改变经历突变的谱系状态。每个突变将谱系的等位状态转变为种群中不存在的新等位,从而在现存谱系中产生多种等位状态。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/50c6e8bd0db320117516bcd3035d336593a3596ab43993170e01e82112084ed8.jpg]]<br />
| |
| 图5.18 在单一有限种群中溯祖与突变同时发生过程下构建的系谱图。此处假设DNA序列突变的无限位点模型以确定系谱图中各谱系的等位状态。通过任意指定最近共同祖先的DNA序列为ACTGCTAGCA,每个突变事件将改变经历突变的谱系DNA序列。每个突变发生在DNA序列中随机选取且此前未经历突变的位点(红色小写字母标记的碱基),导致现存谱系间DNA序列的差异。此处假设每个碱基通过突变产生的概率相等,尽管存在多种模型可规定预期的核苷酸变化模式。在有限位点突变模型下,DNA序列中的每个位点可能经历重复突变。
| |
|
| |
| 当包含突变的谱系与突变模型结合时,可明确预测在影响分支模式的各类过程下预期的等位基因状态多样性和类型。尽管这里展示的两个案例都利用了有限种群中遗传漂变产生的谱系,但突变也可与其他过程结合——如种群结构、种群规模增长或缩减、或用于生成溯祖谱系的自然选择。第7章将介绍自然选择下的谱系预期,第8章则阐述比较不同群体遗传过程生成的谱系中等位基因状态预期模式的方法。
| |
|
| |
| = 第5章回顾 =
| |
|
| |
| 突变是产生新遗传多态性的基本过程。突变率估计可通过观察报告基因座、波动实验、突变积累品系以及相关个体间DNA序列的直接比对获得。虽然精确估计突变率仍具挑战性,但全基因组测序极大改善了单倍体基因组每代突变率(U)的估计,因为基因组的大部分区域均可被观测。通过突变积累品系常可估计的基因型相对适合度谱,揭示了新突变的相对适合度分布,表明大多数突变具有有害性。
| |
|
| |
| 强有害或致死突变将被自然选择清除,而强有利突变将被自然选择固定。效应较小的突变可能呈中性或近中性,因此将受制于遗传漂变导致的随机固定或丢失。
| |
|
| |
| 新突变可能通过孟德尔式分离直接丢失,因为单个等位基因有<math display="inline">\left({\frac{1}{2}}\right)^{l}</math>的概率不传递给<math display="inline">k</math>个子代。中性突变最终必然丢失,而新出现的有利突变逃脱丢失(即被固定)的概率约等于其选择优势的两倍——该结论基于种群规模极大的假设。
| |
|
| |
| 新中性突变的初始频率为<math display="inline">\frac{1}{2N_{e}}</math>,因此固定概率为<math display="inline">\frac{1}{2N_{e}}</math>,丢失概率为<math display="inline">1-\frac{1}{2N_{e}}</math>。绝大多数新中性突变预期会从种群中迅速消失,因其初始频率极近0。对于最终被固定的突变,其固定时间平均为<math display="inline">4N_{e}</math>代。在扩张种群边缘发生的中性、有害或有利突变,可能通过随机突变冲浪达到高频。
| |
|
| |
| Fisher的突变几何模型表明,对表型影响较小的突变更可能被自然选择固定,因为这些突变具有最大概率提升适合度。
| |
|
| |
| 在缺乏或限制重组的基因组中,突变、遗传漂变与自然选择的共同作用会导致有害突变不断积累,这种现象称为''Muller’s Ratchet''。
| |
|
| |
| <span id="突变模型-1"></span>
| |
| = 突变模型 =
| |
|
| |
| '''无限等位基因模型'''假设离散的等位基因状态,其中每次突变都会产生一个种群中当前不存在的等位基因。'''无限位点模型'''假设等位基因是DNA序列,且每次突变仅改变一个从未经历过突变的核苷酸位点。由于在这两种模型中,突变无法两次形成相同的等位基因,因此'''状态同一性'''始终等同于'''血统同一性'''。遗传距离测量通过突变模型量化种群内等位基因状态之间频率加权的差异。突变模型的作用可通过<math display="inline">R_{ST}</math>(一种利用逐步突变模型的<math display="inline">F_{ST}</math>估计量)来说明,该模型假设状态更接近的等位基因更可能具有较近的亲缘关系。
| |
|
| |
| DNA序列的突变模型包括'''无限位点模型'''(以避免同塑性)和'''有限位点模型'''(同塑性由同一核苷酸位点的多次突变产生)。'''不可逆突变'''最终会导致种群中原始等位基因的丢失,因为没有过程能恢复原始等位基因。'''双向突变'''会导致两个等位基因状态的净平衡,以及取决于正向和反向突变率的中间等位基因频率。两种模型均表明,仅靠突变需数千或数万代(取决于突变率)才能使种群达到平衡等位基因频率。
| |
|
| |
| 在无限等位基因模型下,'''遗传漂变'''与突变的平衡可预测平衡杂合度为<math display="inline">\frac{\theta}{\theta+1}</math>,其中<math display="inline">\uptheta=4N_{e}\upmu</math>为有效突变率。
| |
|
| |
| 突变过程可通过建模'''累积指数分布'''的任意事件等待时间,加入到溯祖系谱中。当事件发生时,可能是'''溯祖'''或'''突变''',并反映在系谱中。由于突变概率随时间恒定,系谱中较长的分支更可能发生更多突变。
| |
|
| |
| 系谱中的每个突变事件可在特定突变模型(如无限等位基因或无限位点)下解释。包含突变的溯祖系谱与突变模型结合,可预测产生该系谱的过程所预期的等位基因数量及频率。
| |
|
| |
|
| |
| -----
| |
|
| |
| = 延伸阅读 =
| |
|
| |
| 一位演化遗传学领域的重要学者主张突变应被视为演化的核心过程:
| |
|
| |
| Nei, M. (2013). ''Mutation-Driven Evolution''. Oxford: Oxford University Press.
| |
|
| |
| 关于早期突变率研究的历史及直接参与科学家的角色,参见:
| |
|
| |
| Peter, D., Keightley, P.D., and Adam, E.-W.A. (1999). Terumi Mukai and the riddle of deleterious mutation rates. ''Genetics'' 153: 515–523.
| |
|
| |
| 基于全基因组测序的突变率估计的详细综述:
| |
|
| |
| Katju, V. and Bergthorsson, U. (2019). Old trade, new tricks: insights into the spontaneous mutation process from the partnering of classical mutation accumulation experiments with high-throughput genomic approaches. ''Genome Biology and Evolution'' 11: 136–165.
| |
|
| |
| = 章节末练习题 =
| |
|
| |
| 1 解释用于估计每个核苷酸突变率的不同方法。每种方法可能的优势与劣势是什么?<br />
| |
| 2 解释突变率演化的漂移屏障假说(drift barrier hypothesis)。它与突变适应度谱(mutation fitness spectrum)有何关联?该假说预测了什么?<br />
| |
| 3 从自合子性(autozygosity)和溯祖(coalescence)的角度,解释有效突变率 <math display="inline">\uptheta=4N_{e}\upmu</math> 所预测的内容。纯合度(homozygosity)与杂合度(heterozygosity)如何随有效突变率变化?原因是什么?<br />
| |
| 4 突变率和突变状态变化如何影响遗传多态性实证研究中遗传标记的选择?有效的遗传标记位点需具备哪些特征?<br />
| |
| 5 在穆勒棘轮(Muller’s Ratchet)模型中,若同时存在重组作用,会发生什么?<br />
| |
| 6 使用教材模拟网站 ''Simulations -> Drift Selection Mutation'' 完成本题。勾选突变选项使漂移和突变同时作用(自然选择不参与)。运行模拟并关注右侧条形图。该条形图显示了什么?调整 <math display="inline">N_{e}</math> 和 <math display="inline">\upmu</math> 的模拟参数以获得不同有效突变率 <math display="inline">\uptheta=4N_{e}\upmu</math> 值。例如,分别以 <math display="inline">N_{e}</math> 为 5、20、100、500、2000 运行模拟。图中模式如何随 θ 变化?观察到的模式如何依赖于双向突变模型(two-way mutation model)?<br />
| |
| 7 根据互动框 5.5 的指导,为六个谱系(<math display="inline">k=6</math>)构建包含突变的溯祖家系(coalescent genealogy)。使用 <math display="inline">2N=50</math> 和突变率 0.05(注:此突变率过高以确保产生足够多突变事件。若生成的家系无突变,请更换随机数重试)。用坐标纸绘制家系图,并在连续时间和离散时间尺度上标注突变与溯祖事件的时序。
| |
|
| |
| 为最近共同祖先(MRCA)分配离散等位基因状态“A”,然后基于无限等位基因模型(infinite alleles model)为当前谱系分配等位基因状态。在随机交配下,群体中等位基因频率、基因型频率、预期纯合度与杂合度各是多少?
| |
|
| |
| 8 根据互动框 5.5 的指导,为六个谱系(<math display="inline">\mathit{\Theta}_{k}=6\mathit{\Theta}_{,}</math>)构建包含突变的溯祖家系。使用 <math display="inline">2N=50</math> 和突变率 0.05(注:此突变率过高以确保产生足够多突变事件。若生成的家系无突变,请更换随机数重试)。用坐标纸绘制家系图,并在连续时间和离散时间尺度上标注突变与溯祖事件的时序。
| |
|
| |
| = 第6章 =
| |
|
| |
| === 自然选择的基础 ===
| |
|
| |
| <span id="自然选择"></span>
| |
| ==== 6.1 自然选择 ====
| |
|
| |
| • 将达尔文的思想转化为模型。<br />
| |
| 自然选择作为差异种群增长。<br />
| |
| 克隆繁殖下的自然选择。<br />
| |
| 有性繁殖下的自然选择及其假设。
| |
|
| |
| 查尔斯·达尔文(Charles Darwin,1859)对自然选择过程的阐述可总结为关于种群的三个基本观察:
| |
|
| |
| 所有物种产生的后代数量都超过可能存活并繁殖的数量,<br />
| |
| 个体在表型上存在差异,这些表型会影响其生存和繁殖能力,且<br />
| |
| 每一代中,拥有更高生存和繁殖能力表型的个体将向下一代贡献更多后代。
| |
|
| |
| 结果是,能可靠提高生存和繁殖机会的表型将在世代间频率增加——前提是此类性状具有遗传基础。达尔文的观察最初作为定性模型存在,因为当时缺乏准确的遗传继承模型,直至孟德尔(Mendel)的研究成果被认可。一旦颗粒遗传理论被理解,遗传学与自然选择原理的统一便形成了如今所称的现代综合(modern synthesis)或新达尔文综合(neo-Darwinian synthesis)进化生物学。现代综合对群体遗传学的主要挑战是发展关于自然选择引起的遗传变化的预期。本章本节将阐述这些基本的群体遗传预期。
| |
|
| |
| ==== 克隆繁殖下的自然选择 ====
| |
|
| |
|
| |
| -----
| |
|
| |
| (注:用户未提供完整原始文本,此处仅翻译已提交部分。学名、人名、术语均按要求保留原文,斜体格式已应用。)
| |
|
| |
| 自然选择的核心实际上是一个种群增长的过程,因此让我们从考察一个简单的种群增长模型开始。假设种群大小没有上限,则未来一代的个体数量<math display="inline">(N_{t+1})</math>是当前个体数量<math display="inline">(N_{t})</math>乘以种群的有限增长率<math display="inline">\lambda</math>(读作”lambda”)的乘积,表达式为:
| |
|
| |
| <math display="block">
| |
| N_{t+1}=\lambda N_{t}
| |
| </math>
| |
|
| |
| 在这个无界种群增长模型中,<math display="inline">\lambda</math>是一个乘数,代表每代因死亡而损失的个体数量与通过繁殖新增个体数量之间的净差值。如果出生数与死亡数完全相等,则<math display="inline">\lambda=1</math>,种群大小不变。若出生数多于死亡数,则<math display="inline">\lambda>1.0</math>,种群增长;反之,若死亡数多于出生数,则<math display="inline">\lambda<1.0</math>,种群缩减。种群增长率可理解为个体为下一代贡献一个后代的概率。
| |
|
| |
| 自然选择实际上只是这个基础种群增长模型的特例——每个基因型具有自身的增长率。为理解其机制,让我们考虑一个由两种基因型组成的种群,例如通过克隆分裂进行离散世代繁殖的无性生殖生物(如细菌物种)。将两种基因型称为A和B,其基因型特异性增长率或绝对适合度值分别为<math display="inline">\lambda_{\mathrm{A}}</math>和<math display="inline">\lambda_{\mathrm{B}}</math>。每一代中各基因型在总种群中的比例为:
| |
|
| |
| <math display="block">
| |
| p={\frac{N_{\mathrm{A}}}{N_{\mathrm{A}}+N_{\mathrm{B}}}}
| |
| </math>
| |
|
| |
| 与
| |
|
| |
| <math display="block">
| |
| q={\frac{N_{\mathrm{B}}}{N_{\mathrm{A}}+N_{\mathrm{B}}}}
| |
| </math>
| |
|
| |
| 其中<math display="inline">N_{\mathrm{A}}+N_{\mathrm{B}}</math>为总种群大小。图6.1A展示了随时间推移的个体数量变化示例:基因型A比基因型B增长更快。就绝对个体数量而言,两种基因型的种群规模均随时间增加。然而,种群中A和B基因型个体的比例随时间发生改变(图6.1B)。由于A基因型增长更快,A个体在总种群中所占比例持续上升。这等同于说<math display="inline">p</math>随时间增加而<math display="inline">q</math>随时间减少。
| |
|
| |
| 因此,图6.1展示了自然选择偏向A基因型的情况,因其具有更高的绝对适合度水平。
| |
|
| |
| 另一种表示种群中两种基因型比例变化的方法是追踪A与B个体数量的比值<math display="inline">\begin{array}{r}{N_{\mathrm{A}}/N_{\mathrm{B}},}\end{array}</math>随时间的变化。该比值在任何时刻的值取决于A和B个体的初始数量(记为<math display="inline">N_{\mathrm{A}}(0)</math>和<math display="inline">N_{\mathrm{B}}(0)</math>)、两种基因型的增长率以及经过的世代数。经过一代种群增长后,比值<math display="inline">N_{\mathrm{B}}/N_{\mathrm{A}}</math>由下式给出:
| |
|
| |
| <math display="block">
| |
| {\frac{N_{\mathrm{B}}(t=1)}{N_{\mathrm{A}}(t=1)}}=\left({\frac{\lambda_{\mathrm{B}}}{\lambda_{\mathrm{A}}}}\right){\frac{N_{\mathrm{B}}(0)}{N_{\mathrm{A}}(0)}}
| |
| </math>
| |
|
| |
| 这类似于将基因型A的方程6.1版本除以基因型B的方程6.1版本。通常,我们可以通过假设基因型特异性增长率(<math display="inline">\lambda_{\mathrm{A}}</math>和<math display="inline">\lambda_{\mathrm{B}}</math>)随时间保持恒定,使用下式预测任意时间t的<math display="inline">N_{\mathrm{A}}/N_{\mathrm{B}}</math>比值:
| |
|
| |
| <math display="block">
| |
| {\frac{N_{\mathrm{B}}(t)}{N_{\mathrm{A}}(t)}}=\left({\frac{\lambda_{\mathrm{B}}}{\lambda_{\mathrm{A}}}}\right)^{t}{\frac{N_{\mathrm{B}}(0)}{N_{\mathrm{A}}(0)}}
| |
| </math>
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/d07d54ecbe24548a661323551f685aca01a9113f461528c8a9f5d2dd8bdaa3e4.jpg]]<br />
| |
| 图6.1 两种克隆繁殖基因型的种群增长情况。初始个体数量相等,因此在总种群中比例相同。基因型A每代增长3%(<math display="inline">\lambda=1.03</math>),基因型B每代增长1%(<math display="inline">\lambda=1.01</math>)。两个基因型的个体数量均随时间增加(图A)。由于增长率不同,它们在总种群中的相对比例随时间变化(图B)。实线显示初始的等比例状态。最终,基因型A将接近总种群的100%,而基因型B接近0%。数值每三代绘制一次。
| |
|
| |
| 基因型特异性增长率的比值称为相对适合度,在离散世代自然选择模型中用符号<math display="inline">w</math>表示。将方程6.5中的基因型特异性增长率比值替换为相对适合度可得:
| |
|
| |
| <math display="block">
| |
| {\frac{N_{\mathrm{B}}(t)}{N_{\mathrm{A}}(t)}}=w^{t}{\frac{N_{\mathrm{B}}(0)}{N_{\mathrm{A}}(0)}}
| |
| </math>
| |
|
| |
| 注意到<math display="inline">N_{\mathrm{A}}+N_{\mathrm{B}}</math>给出任意时刻总种群大小<math display="inline">N</math>,将方程6.6两边乘以<math display="inline">\frac{\frac{1}{N}}{\frac{1}{N}}</math>可得:
| |
|
| |
| <math display="block">
| |
| \begin{array}{r}{\frac{N_{\mathrm{B}}(t)}{N}=w^{t}\frac{\frac{N_{\mathrm{B}}(0)}{N}}{\frac{N_{\mathrm{A}}(0)}{N}}}\end{array}
| |
| </math>
| |
|
| |
| 利用方程6.2和6.3可简化为:
| |
|
| |
| <math display="block">
| |
| \frac{q_{t}}{p_{t}}=w^{t}\frac{q_{0}}{p_{0}}
| |
| </math>
| |
|
| |
| 这表示各基因型在任意时间t占总种群的比例。当<math display="inline">w=1.0</math>时,两种基因型具有相同的增长率,各自比例随时间保持恒定。若<math display="inline">w>1.0</math>,则分子中的基因型比分母中的生长更快,其种群比例将随时间增加。反之,若<math display="inline">w<1.0</math>,则分子中的基因型生长较慢,其比例将随时间减少。以A基因型为参照标准,结合图6.1的绝对适合度值,<math display="inline">\begin{array}{l l l l l}{{w_{A}}}&{{=}}&{{1.03/1.03}}&{{=}}&{{1.0}}\end{array}</math>且<math display="inline">w_{B}~=~1.01/</math> <math display="inline">1.03=0.981</math>,因此A基因型的频率预计将随时间增加。
| |
|
| |
| 相对适合度可用于确定基因型频率随时间的变化,如表6.1所示。基因型频率的变化是两代之间的频率差,即<math display="inline">p_{t+1}-p_{t}</math>。这种差异通常用希腊大写字母delta(Δ)表示,因此A基因型频率的变化可表示为<math display="inline">\varDelta p=p_{t+1}-p_{t}</math>。为了推导<math display="inline">\varDelta p</math>的表达式,我们可以比较初始基因型频率<math display="inline">p_{t}</math>与经历自然选择后的频率。我们从基因型频率差异的基本表达式开始:
| |
|
| |
| 表6.1 克隆繁殖情形下自然选择后两种基因型的预期频率。表格上半部分给出一般情况的表达式,下半部分使用与图6.1相同的绝对和相对适合度值,展示自然选择第一代的基因型比例变化。A基因型的绝对适合度最高,因此在确定相对适合度时作为比较标准。
| |
|
| |
| {|
| |
| !width="42%"|
| |
| !width="28%"| Genotype A
| |
| !width="28%"| Genotype B
| |
| |-
| |
| | '''Generation t'''
| |
| |
| |
| |
| |
| |-
| |
| | 初始频率
| |
| | <math display="inline">p_{t}</math>
| |
| | <math display="inline">q_{t}</math>
| |
| |-
| |
| | 基因型特异性增长率(绝对适合度)
| |
| | <math display="inline">N_A</math>
| |
| | <math display="inline">\lambda_B</math>
| |
| |-
| |
| | 相对适合度
| |
| | <math display="inline">W_A=\frac{\lambda_A}{\lambda_A}</math>
| |
| | <math display="inline">W_B=\frac{\lambda_B}{\lambda_A}</math>
| |
| |-
| |
| | 自然选择后频率
| |
| | <math display="inline">\frac{p_{t}W_A}{p_{t}W_A + q_{t}W_B}</math>
| |
| | <math display="inline">\frac{q_{t}W_B}{p_{t}W_A + q_{t}W_B}</math>
| |
| |-
| |
| | '''Generation t+1'''
| |
| |
| |
| |
| |
| |-
| |
| | 初始频率<math display="inline">p_{t+1}</math>
| |
| | <math display="inline">\frac{p_{t}W_A}{p_{t}W_A + q_{t}W_B}</math>
| |
| | <math display="inline">\frac{q_{t}W_B}{p_{t}W_A + q_{t}W_B}</math>
| |
| |-
| |
| | 基因型频率变化
| |
| | <math display="inline">\Delta p = p_{t+1} - p_{t}</math>
| |
| | <math display="inline">\Delta q = q_{t+1} - q_{t}</math>
| |
| |}
| |
|
| |
| {|
| |
| !width="42%"|
| |
| !width="28%"| Genotype A
| |
| !width="28%"| Genotype B
| |
| |-
| |
| | '''Generation t'''
| |
| |
| |
| |
| |
| |-
| |
| | 初始频率
| |
| | <math display="inline">p_{t}=0.5</math>
| |
| | <math display="inline">q_{t}=0.5</math>
| |
| |-
| |
| | 基因型特异性增长率(绝对适合度)
| |
| | <math display="inline">\lambda_A=1.03</math>
| |
| | <math display="inline">\lambda_B=1.01</math>
| |
| |-
| |
| | 相对适合度
| |
| | <math display="inline">W_A=\frac{\lambda_A}{\lambda_A}=1.0</math>
| |
| | <math display="inline">W_B=\frac{\lambda_B}{\lambda_A}=0.981</math>
| |
| |-
| |
| | 自然选择后频率
| |
| | <math display="inline">p_{t}W_A=(0.5)(1.0)=0.5</math>
| |
| | <math display="inline">q_{t}W_B=(0.5)(0.981)=0.4905</math>
| |
| |-
| |
| | '''Generation t+1'''
| |
| |
| |
| |
| |
| |-
| |
| | 初始频率<math display="inline">p_{t+1}</math>
| |
| | <math display="inline">\frac{0.5}{0.5+0.4905}=0.5048</math>
| |
| | <math display="inline">\frac{0.4905}{0.5+0.4905}=0.4952</math>
| |
| |-
| |
| | 基因型频率变化
| |
| | <math display="inline">0.5048-0.5=0.0048</math>
| |
| | <math display="inline">0.4952-0.5=-0.0048</math>
| |
| |}
| |
|
| |
| <math display="block">
| |
| \Delta p=p_{t+1}-p_{t}
| |
| </math>
| |
|
| |
| 当<math display="inline">\varDelta p</math>为正值时,A基因型在种群中的比例将增加;当<math display="inline">\varDelta p</math>为负值时,其比例将减少。将自然选择后A基因型的预期频率表达式(表6.1)代入可得:
| |
|
| |
| <math display="block">
| |
| \Delta p=\frac{p_{t}w_{\mathrm{A}}}{p_{t}w_{\mathrm{A}}+q_{t}w_{\mathrm{B}}}-p_{t}
| |
| </math>
| |
|
| |
| 式6.10右侧分母中的<math display="inline">p_{t}w_{\mathrm{A}}+q_{t}w_{\mathrm{B}}</math>项表示种群的'''平均相对适合度'''(这是一个频率加权平均值,因此取决于各基因型频率与相对适合度的乘积之和)。当A基因型在自然选择后的频率超过两种基因型在自然选择后的平均适合度时,<math display="inline">\varDelta p</math>呈现正值。表6.1中的计算表明,A基因型频率乘以其相对适合度<math display="inline">\left(p_{t}w_{\mathrm{A}}\right)</math>大于平均适合度,因此A基因型在种群中的比例将随时间增加。平均适合度将在讨论有性二倍体种群的天然选择时进行更详细的阐述。
| |
|
| |
| 使用相对适合度的优势在于,无需知晓各基因型的种群增长率即可模拟基因型比例随时间的变化。相反,基因型相对频率的生长过程结果仅通过增长率比值即可预测。这意味着式6.8既适用于绝对增长率极高的生物(如细菌),也适用于绝对增长率接近1的物种(如大象)。式6.8甚至适用于种群规模随时间递减的情况。若某种群因所有基因型的增长率均小于1而趋于灭绝,相对适合度仍能准确反映基因型比例随时间的变化。实践中,可通过竞争实验估算相对适合度——将两种或多种基因型置于同一环境,并在后续时间点测定其比例(见问题框6.1)。
| |
|
| |
| '''绝对适合度''':预测种群中特定基因型个体绝对数量随时间变化的基因型特异性增长率或种群增长速率。常用符号为<math display="inline">W</math>或<math display="inline">\lambda</math>。<br />
| |
| '''平均适合度'''<math display="inline">(\overline{{\boldsymbol{w}}})</math>:种群中各基因型相对适合值的频率加权和。<br />
| |
| '''相对适合度''':基因型相对于某标准基因型(通常选择具有最高绝对适合度的基因型)的增长率。在以离散世代表示时间的模型中称为达尔文适合度(Darwinian fitness,源自Charles Darwin),符号为<math display="inline">w</math>;在连续时间模型中称为马尔萨斯适合度(Malthusian fitness,源自Thomas Malthus),符号为<math display="inline">m</math>。
| |
|
| |
| 尽管存在简化假设,克隆繁殖生物中基因型间自然选择的模型仍适用于多种实际场景。例如人类免疫缺陷病毒(HIV)通过自然选择演化出药物抗性的过程。HIV(及其他逆转录病毒)的基因组为单链RNA。病毒颗粒内部的所有蛋白质及病毒包膜蛋白均由该RNA基因组编码。感染宿主细胞后,HIV利用自身基因编码的逆转录酶将基因组反转录为双链DNA。这种逆转录病毒基因组的DNA版本随后整合至宿主
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/3b440b267443a457a059e23e7724bd62869b615fc49b3e48aa3d91bb64bf5b6b.jpg]]<br />
| |
| 图6.2 两名接受蛋白酶抑制剂(ritonavir)治疗患者体内HIV种群蛋白酶基因座等位基因频率随时间变化(Doukhan和Delwart 2001)。药物治疗前低频存在的等位基因,由于HIV基因型间对耐药性的自然选择,在药物治疗后成为种群优势。等位基因通过变性梯度凝胶电泳(DGGE)观察到的条带显示,该技术可区分不同DNA片段间单个碱基对的差异。DGGE用于检测HIV颗粒样本中蛋白酶基因座DNA序列的多样性。蛋白酶抑制剂治疗起始于第0天。原始数据由E. Delwart博士惠赠。
| |
|
| |
| 病毒RNA基因组通过逆转录转化为双链DNA,随后整合到宿主细胞DNA中,并在宿主细胞内转录产生大量新病毒RNA基因组。这些新病毒RNA基因组通过病毒蛋白酶介导的宿主细胞释放过程被包装成病毒颗粒。针对HIV的一种治疗策略是使用模拟核苷(无磷酸基团的核苷酸)类药物,这类药物可干扰病毒逆转录酶活性而不影响宿主细胞DNA聚合酶。另一种疗法采用蛋白酶抑制剂,通过干扰产生新感染性病毒颗粒所必需的多蛋白切割过程。遗憾的是,HIV通过自然选择快速演化出耐药基因型。图6.2显示了两名患者(第0天开始蛋白酶抑制剂治疗)体内HIV种群等位基因频率随时间的变化。携带耐药蛋白酶等位基因的HIV颗粒比野生型蛋白酶等位基因的HIV颗粒具有更高的复制速率。这种HIV基因型的差异生长率,即蛋白酶基因座的自然选择作用,快速改变了每位患者体内HIV种群的蛋白酶基因等位基因频率。短世代周期、高突变率和大有效种群规模的共同作用,使得自然选择成为快速改变HIV种群等位基因频率的演化动力。
| |
|
| |
| <span id="问题框6.1-hiv基因型的相对适合度"></span>
| |
| = 问题框6.1 HIV基因型的相对适合度 =
| |
|
| |
| 普遍认为,在无药物暴露环境下,耐药等位基因的相对适合度低于非耐药等位基因。为验证HIV-1的这一假设,Goudsmit等(1996)监测了新感染HIV(未接受核苷类似物azidothymidine/AZT治疗)个体逆转录酶基因215密码子等位基因频率的变化。初始阶段,HIV等位基因全为已知可赋予AZT耐药性的序列(90% TAC和10% TCC密码子)。随时间推移,非耐药等位基因(TTC密码子)频率在20个月内上升至49%。
| |
|
| |
| 利用这601天内等位基因频率的变化和方程6.8(Eq. 6.8),估算非抗性等位基因在无AZT情况下的相对适合度。假设HIV的世代时间为2.6天且世代是离散的,且野生型等位基因的初始频率为<math display="inline">1.0\%</math>,因此最初无法被检测到。注意,形如<math display="inline">a=\gamma(x^{t})</math>的方程(其中<math display="inline">a,\gamma,</math>和<math display="inline">\boldsymbol{X}</math>为常数)可通过取两边的对数来消去指数,得到<math display="inline">\log(a)=\log(y)+t\log(x)</math>。
| |
|
| |
| 自然选择的单倍体模型在存在多重有益突变时提出了一个值得注意的预测。当种群中存在两个或更多有益单倍型且无重组时,会预测到一种称为克隆干扰(clonal interference)的现象(Muller 1932)。多重有益单倍型会相互竞争,最终只有适应度最高的单倍型会固定,而其他有益单倍型将走向消失。通过考虑<math display="inline">\lambda_{\mathrm{A}}</math>和<math display="inline">\lambda_{\mathrm{B}}</math>均大于1的例子(如图6.1中的单倍型),可以理解克隆干扰。尽管A和B单倍型个体的种群规模会随时间增长,但它们的相对适合度值可预测其相对频率的变化,并表明最终仅有一种单倍型会固定。克隆干扰预测,如果众多有益突变在种群中同时分离,单倍体的自然选择将无法维持并固定这些突变。在缺乏重组的生物(如细菌(Imhof和Schlötterer 2001)和酵母(Lang等2013))中已观察到克隆干扰在有益突变间存在的经验证据。这表明,当重组缺失时,单倍型原有的适应度可影响新有益突变的命运,种群中其他单倍型的相对适应度亦是如此。
| |
|
| |
| 还需注意,若<math display="inline">\lambda_{\mathrm{A}}</math>和<math display="inline">\lambda_{\mathrm{B}}</math>均小于1,则A和B单倍型个体的种群最终将走向灭绝。然而,随着两种单倍型种群的缩减,具有更高相对适合度的单倍型频率仍会随时间上升,因为其减少速率低于其他单倍型。由于相对适合度预测的是单倍型的未来频率而非其绝对种群规模,相对适合度并非研究自然选择与种群灭绝关系的合适指标。
| |
|
| |
| <span id="natural-selection-with-sexual-reproduction"></span>
| |
| ==== Natural selection with sexual reproduction ====
| |
|
| |
| 在克隆繁殖的自然选择模型中,许多生物的关键生物学部分被忽略了,即有性生殖。为了构建有性生殖的自然选择模型,我们可以将基因型频率的'''Hardy–Weinberg模型'''与基因型特异性生长速率相结合,得到一个作用于由双等位基因单一位点产生的三种基因型的自然选择通用模型。这两个模型的融合引出了一系列假设,如表6.2所列(对比第2章单独列出的Hardy–Weinberg假设)。目前,我们采用能推导出预期基因型频率的假设。本章后续将探讨其他假设的后果。
| |
|
| |
| 假设一个由<math display="inline">N</math>个二倍体个体组成的种群,其亲本通过随机交配产生配子,随后配子随机融合形成合子。当<math display="inline">N</math>个合子刚形成时(即自然选择作用前),基因型处于'''Hardy–Weinberg'''预期频率。若此时总种群大小为<math display="inline">N_{t}</math>,则每种基因型的合子数量为:
| |
|
| |
| {|
| |
| !width="11%"| 遗传
| |
| !width="23%"| 二倍体个体
| |
| !width="38%"| 双等位基因单一位点
| |
| !width="26%"| 专性有性生殖
| |
| |-
| |
| | 繁殖
| |
| | 世代不重叠
| |
| | 随机交配
| |
| |
| |
| |-
| |
| | 自然选择
| |
| | 自然选择机制为基因型特异性存活率(适合度)差异,导致基因型特异性生长速率差异,称为'''生存力选择'''
| |
| | 适合度值为常数,不随时间、空间或两性变化
| |
| |
| |
| |-
| |
| | 种群
| |
| | 无限种群大小(无遗传漂变)
| |
| | 无种群结构
| |
| | 无基因流
| |
| |}
| |
|
| |
| <math display="block">
| |
| \mathrm{AA}:p^{2}N_{t}\quad\mathrm{Aa}:2p q N_{t}\quad\mathrm{aa}:q^{2}N_{t}
| |
| </math>
| |
|
| |
| 这定义了三种基因型的初始数量,类似于克隆繁殖模型中使用的<math display="inline">N_{\mathrm{A}}(0)</math>和<math display="inline">N_{\mathrm{B}}(0)</math>。
| |
|
| |
| 合子初始种群形成后,自然选择将对三种基因型发挥作用。在单一位点选择模型的假设下,自然选择机制采取特定形式:如图6.3所示,每个基因型在单世代周期内经历基因型特异性存活和繁殖。这可能导致各基因型合子数量在生命周期初期减少。目前假设任何基因型个体数量的减少仅源于未能存活至生殖年龄,但所有存活成体的繁殖能力与基因型无关。此时,各基因型的适合度值代表存活至繁殖的概率,称为'''生存力''',而自然选择表现为'''生存力选择'''。
| |
|
| |
| '''生存力选择(Viability selection)''':一种自然选择形式,其中适合度等于特定基因型个体存活至生殖年龄的概率,但所有存活个体的繁殖率相同。
| |
|
| |
| '''边际适合度(Marginal fitness)''':含特定等位基因的基因型相对适合度值的频率加权与等位基因拷贝数加权之和;仅针对含某等位基因的基因型的平均适合度特例。
| |
|
| |
| 作為克隆繁殖中使用的<math display="inline">\lambda</math>的類比,令<math display="inline">\ell</math>(斜體字母l)代表基因型特異性的存活到繁殖年齡的概率。經過生存力選擇後,在繁殖時點的各基因型個體數為
| |
|
| |
| <math display="block">
| |
| \mathrm{AA}:\ell_{\mathrm{AA}}p^{2}N_{t}\quad\mathrm{Aa}:\ell_{\mathrm{Aa}}2p q N_{t}\quad\mathrm{aa}:\ell_{\mathrm{aa}}q^{2}N_{t}
| |
| </math>
| |
|
| |
| 這些是各基因型個體的數量,它們將參與隨機交配以形成下一代。選擇後群體的總個體數為
| |
|
| |
| <math display="block">
| |
| \ell_{\mathrm{AA}}p^{2}N_{t}+\ell_{\mathrm{Aa}}2p q N_{t}+\ell_{\mathrm{aa}}q^{2}N_{t}
| |
| </math>
| |
|
| |
| 此數值可用於確定選擇後群體中基因型或等位基因的頻率。例如,選擇後由AA基因型個體組成的總群體比例為
| |
|
| |
| AA基因型的頻率
| |
|
| |
| <math display="block">
| |
| =\frac{\ell_{\mathrm{AA}}p^{2}N_{t}}{\ell_{\mathrm{AA}}p^{2}N_{t}+\ell_{\mathrm{Aa}}2p q N_{t}+\ell_{\mathrm{aa}}q^{2}N_{t}}
| |
| </math>
| |
|
| |
| 由於等位基因的數量少於基因型,自然選擇的結果通常以等位基因頻率而非基因型頻率來總結。在存活個體產生的配子中,等位基因的頻率(根據表6.2的假設)為
| |
|
| |
| 配子中A等位基因的頻率
| |
|
| |
| <math display="block">
| |
| =\frac{\ell_{\mathrm{AA}}p^{2}N_{t}+\frac{1}{2}\left(\ell_{\mathrm{Aa}}2p q N_{t}\right)}{\ell_{\mathrm{AA}}p^{2}N_{t}+\ell_{\mathrm{Aa}}2p q N_{t}+\ell_{\mathrm{aa}}q^{2}N_{t}}
| |
| </math>
| |
|
| |
| 及
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/3e035957a8dacb80b2f69f3d64c0de6a3ab4b3714ae3f61636ac8ad40289fce1.jpg]]<br />
| |
| '''圖6.3''' 生物體生命週期圖示,標明基因型間差異存活與繁殖可能導致自然選擇的關鍵節點。Viability是從受精卵到成體的存活概率,mating success涵蓋影響交配機會及配偶數量的性狀,fecundity是每對交配個體產生的配子及子代受精卵數量。Gametic compatibility是配子成功融合形成受精卵的概率,而meiotic drive是導致配子中等位基因頻率偏斜的任何機制。大多數自然選擇模型假設單一適合度組件如viability。實際上,所有這些適合度組件可能同時影響基因型頻率。
| |
|
| |
| 配子中a等位基因的頻率
| |
|
| |
| <math display="block">
| |
| \mathrm{~\boldmath~\lambda~}=\frac{\ell_{\mathrm{{aa}}}q^{2}N_{t}+\frac{1}{2}(\ell_{\mathrm{Aa}}2p q N_{t})}{\ell_{\mathrm{AA}}p^{2}N_{t}+\ell_{\mathrm{Aa}}2p q N_{t}+\ell_{\mathrm{{aa}}}q^{2}N_{t}}
| |
| </math>
| |
|
| |
| 在這些方程中,雜合子個體數量乘以1/2,因為一個雜合子對配子庫貢獻的特定等位基因拷貝數,僅為純合子貢獻該等位基因拷貝數的一半。這些表達式可簡化為
| |
|
| |
| 配子中A等位基因的頻率
| |
|
| |
| <math display="block">
| |
| =\frac{\ell_{\mathrm{AA}}p^{2}+\ell_{\mathrm{Aa}}p q}{\ell_{\mathrm{AA}}p^{2}+\ell_{\mathrm{Aa}}2p q+\ell_{\mathrm{aa}}q^{2}}
| |
| </math>
| |
|
| |
| 及
| |
|
| |
| 配子中a等位基因的頻率
| |
|
| |
| <math display="block">
| |
| =\frac{\ell_{\mathrm{aa}}q^{2}+\ell_{\mathrm{Aa}}p q}{\ell_{\mathrm{AA}}p^{2}+\ell_{\mathrm{Aa}}2p q+\ell_{\mathrm{aa}}q^{2}}
| |
| </math>
| |
|
| |
| 因为 <math display="inline">N_{\mathrm{t}}</math> 可以从分子和分母的每一项中提出并约去,且分子中的百分比常数和2也会约去。
| |
|
| |
| 与克隆繁殖的情况类似,我们可以用每种基因型的相对适合度值代替绝对生殖年龄存活率值。因此,我们可以将 <math display="inline">\ell_{\mathrm{AA}},\ell_{\mathrm{Aa}},</math> 和 <math display="inline">\ell_{\mathrm{aa}}</math> 替换为相对适合度值 <math display="inline">w_{\mathrm{AA}},~w_{\mathrm{Aa}}</math>,和 <math display="inline">\boldsymbol{W_{\mathrm{aa}}}</math>,从而得到:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=\frac{w_{\mathrm{AA}}p^{2}+w_{\mathrm{Aa}}p q}{w_{\mathrm{AA}}p^{2}+w_{\mathrm{Aa}}2p q+w_{\mathrm{aa}}q^{2}}
| |
| </math>
| |
|
| |
| 以及
| |
|
| |
| <math display="block">
| |
| q_{t+1}=\frac{w_{\mathrm{aa}}q^{2}+w_{\mathrm{Aa}}p q}{w_{\mathrm{AA}}p^{2}+w_{\mathrm{Aa}}2p q+w_{\mathrm{aa}}q^{2}}
| |
| </math>
| |
|
| |
| 注意这两个表达式中的分母是适合度加权的基因型频率之和,即平均相对适合度 <math display="inline">\overline{{\boldsymbol{W}}}</math>。将其代入后,等位基因频率的表达式可进一步简化为:
| |
|
| |
| <math display="block">
| |
| p_{t+1}={\frac{w_{\mathrm{AA}}p^{2}+w_{\mathrm{Aa}}p q}{\overline{{w}}}}
| |
| </math>
| |
|
| |
| 以及
| |
|
| |
| <math display="block">
| |
| q_{t+1}={\frac{w_{\mathrm{aa}}q^{2}+w_{\mathrm{Aa}}p q}{\overline{{{w}}}}}
| |
| </math>
| |
|
| |
| 这些表达式表明,等位基因频率的增减取决于包含特定等位基因的基因型的平均适合度(分子中的量,称为'''边际适合度''')与种群中所有基因型的平均适合度的比较。当构成边际适合度的基因型个体在给定等位基因频率下具有更高生存力时,边际适合度会更大。表6.3总结了构建一代生存力选择后预期基因型和等位基因频率的关键量。
| |
|
| |
| 与克隆繁殖的情况类似,一代内等位基因频率的变化由 <math display="inline">\varDelta p=p_{t+1}-p_{t}</math> 给出。对于有性生殖:
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p q[p(w_{A A}-w_{A a})+q(w_{A a}-w_{a a})]}{\overline{{w}}}}
| |
| </math>
| |
|
| |
| 以及
| |
|
| |
| <math display="block">
| |
| \Delta q=\frac{p q[q(w_{a a}-w_{A a})-p(w_{A A}-w_{A a})]}{\overline{{w}}}
| |
| </math>
| |
|
| |
| 如数学框6.1所推导。该方程提供了三个符合自然选择直觉的推论:当 <math display="inline">p q=0</math> 或没有遗传变异(即一个等位基因已完全丢失,<math display="inline">\overset{\vartriangle}{p}</math> 或 <math display="inline">q=0</math>)时,等位基因频率不变;当所有适合度值相同(即无自然选择)时,方括号内的项为零,等位基因频率也不变;最后,当适合度差异按等位基因频率加权(即 <math display="inline">p(w_{A A}-w_{A a})</math> 和 <math display="inline">q(w_{A a}-w_{a a})</math> 项)相互抵消导致方括号内值为0时,等位基因频率同样不变。
| |
|
| |
| 需注意的另一点是,上述表达式中常使用实际基因型频率(如 <math display="inline">P_{A A}</math>、<math display="inline">P_{A a}</math> 和 <math display="inline">P_{a a}</math>)而非哈迪-温伯格预期的 <math display="inline">p^{2}</math>、<math display="inline">2p q</math> 和 <math display="inline">q^{2}</math>。这是因为多代自然选择可能导致基因型频率偏离哈迪-温伯格预期值。
| |
|
| |
| 表 6.3 具有有性生殖和随机交配的双等位基因位点经历自然选择后三种基因型的预期频率。在确定相对适应度时,以AA基因型的绝对适应度作为比较标准。
| |
|
| |
| {|
| |
| !width="35%"|
| |
| !width="20%"|
| |
| !width="22%"| Genotype
| |
| !width="20%"|
| |
| |-
| |
| |
| |
| | ''AA''
| |
| | ''Aa''
| |
| | ''aa''
| |
| |-
| |
| | Generation t
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | Initial frequency
| |
| | <math display="inline">p_t^2</math>
| |
| | <math display="inline">2p_tq_t</math>
| |
| | <math display="inline">q_t^2</math>
| |
| |-
| |
| | Genotype-specific survival (absolute fitness)
| |
| | <math display="inline">\mathcal{W}_{AA}</math>
| |
| | <math display="inline">\mathcal{W}_{Aa}</math>
| |
| | <math display="inline">\mathcal{W}_{aa}</math>
| |
| |-
| |
| | Relative fitness
| |
| | <math display="inline">W_{AA} = \frac{\mathcal{W}_{AA}}{\mathcal{W}_{AA}}</math>
| |
| | <math display="inline">W_{Aa} = \frac{\mathcal{W}_{Aa}}{\mathcal{W}_{AA}}</math>
| |
| | <math display="inline">W_{aa} = \frac{\mathcal{W}_{aa}}{\mathcal{W}_{AA}}</math>
| |
| |-
| |
| | Frequency after natural selection
| |
| | <math display="inline">\frac{p_t^2 W_{AA}}{\overline{W}}</math>
| |
| | <math display="inline">\frac{2p_tq_t W_{Aa}}{\overline{W}}</math>
| |
| | <math display="inline">\frac{q_t^2 W_{aa}}{\overline{W}}</math>
| |
| |-
| |
| | Average fitness
| |
| | <math display="inline">\overline{W} = p_t^2 W_{AA} + 2p_tq_t W_{Aa} + q_t^2 W_{aa}</math>
| |
| |
| |
| |
| |
| |-
| |
| | Generation t+1
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | Genotype frequency
| |
| | <math display="inline">\frac{p_t^2 W_{AA}}{\overline{W}}</math>
| |
| | <math display="inline">\frac{2p_tq_t W_{Aa}}{\overline{W}}</math>
| |
| | <math display="inline">\frac{q_t^2 W_{aa}}{\overline{W}}</math>
| |
| |-
| |
| | Allele frequency
| |
| | <math display="inline">p_{t+1} = \frac{p_t(p_t W_{AA} + q_t W_{Aa})}{\overline{W}}</math>
| |
| | <math display="inline">q_{t+1} = \frac{q_t(q_t W_{aa} + p_t W_{Aa})}{\overline{W}}</math>
| |
| |
| |
| |-
| |
| | Change in allele frequency
| |
| | <math display="inline">\Delta p = \frac{p_t q_t [p_t(W_{AA} - W_{Aa}) + q_t(W_{Aa} - W_{aa})]}{\overline{W}}</math>
| |
| |
| |
| |
| |
| |}
| |
|
| |
| <span id="数学框-6.1-自然选择下每代等位基因频率的变化"></span>
| |
| = 数学框 6.1 自然选择下每代等位基因频率的变化 =
| |
|
| |
| 为求解自然选择导致的等位基因频率单代变化方程,从下式出发:
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p^{2}w_{\mathrm{AA}}+p q w_{\mathrm{Aa}}}{p^{2}w_{\mathrm{AA}}+2p q w_{\mathrm{Aa}}+q^{2}w_{\mathrm{aa}}}}-p
| |
| </math>
| |
|
| |
| 其中等位基因频率<math display="inline">p</math>和<math display="inline">q</math>均取自同一世代,故省略世代下标。首先将两项通分以便相减:
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p^{2}w_{\mathsf{A A}}+p q w_{\mathsf{A a}}}{p^{2}w_{\mathsf{A A}}+2p q w_{\mathsf{A a}}+q^{2}w_{\mathsf{a a}}}}-{\frac{p\left(p^{2}w_{\mathsf{A A}}+2p q w_{\mathsf{A a}}+q^{2}w_{\mathsf{a a}}\right)}{p^{2}w_{\mathsf{A A}}+2p q w_{\mathsf{A a}}+q^{2}w_{\mathsf{a a}}}}
| |
| </math>
| |
|
| |
| 接着,注意到分子左侧项可提取<math display="inline">p</math>作为因子:
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p(p w_{\mathsf{A A}}+q w_{\mathsf{A a}})}{p^{2}w_{\mathsf{A A}}+2p q w_{\mathsf{A a}}+q^{2}w_{\mathsf{a a}}}}-{\frac{p(p^{2}w_{\mathsf{A A}}+2p q w_{\mathsf{A a}}+q^{2}w_{\mathsf{a a}})}{p^{2}w_{\mathsf{A A}}+2p q w_{\mathsf{A a}}+q^{2}w_{\mathsf{a a}}}}
| |
| </math>
| |
|
| |
| 由此可得(为简化,分母此后记为<math display="inline">\overline{{W}}</math>):
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p\left[p w_{\mathsf{A A}}+q w_{\mathsf{A a}}-p^{2}w_{\mathsf{A A}}-2p q w_{\mathsf{A a}}-q^{2}w_{\mathsf{a a}}\right]}{\overline{{W}}}}
| |
| </math>
| |
|
| |
| 此时利用双等位基因位点中<math display="inline">p=1-q</math>的性质,即<math display="inline">p q=p(1-p)=p-p^{2}</math>。式6.28分子方括号内的第一和第三项<math display="inline">(p w_{\mathsf{A A}}-p^{2}w_{\mathsf{A A}})</math>可改写为<math display="inline">p q w_{\mathsf{A A}}</math>,从而得到:
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p{\big[}p q w_{\mathsf{A A}}+q w_{\mathsf{A a}}-2p q w_{\mathsf{A a}}-q^{2}w_{\mathsf{a a}}{\big]}}{\overline{{W}}}}
| |
| </math>
| |
|
| |
| 接着从方括号内的项中提取公因子<math display="inline">q</math>:
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p q\left[p w_{\mathsf{A A}}+w_{\mathsf{A a}}-2p w_{\mathsf{A a}}-q w_{\mathsf{a a}}\right]}{\overline{{W}}}}
| |
| </math>
| |
|
| |
| 然后,注意方括号中的中间两项——<math display="inline">(w_{\mathrm{Aa}}-2p w_{\mathrm{Aa}})</math>。由于<math display="inline">p+q=1</math>,<math display="inline">W_{\mathrm{Aa}}-</math> <math display="inline">2p w_{\mathsf{A}\mathsf{a}}=(p+q)w_{\mathsf{A}\mathsf{a}}-2p w_{\mathsf{A}\mathsf{a}}=q w_{\mathsf{A}\mathsf{a}}-p w_{\mathsf{A}\mathsf{a}}</math>。代入后得到
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p q{\big[}p w_{\mathsf{A A}}+q w_{\mathsf{A a}}-p w_{\mathsf{A a}}-q w_{\mathsf{a a}}{\big]}}{\overline{{W}}}}
| |
| </math>
| |
|
| |
| 最终可重新整理为
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p q[p(w_{{\mathsf{A A}}}-w_{{\mathsf{A}}{\mathsf{a}}})+q(w_{{\mathsf{A}}{\mathsf{a}}}-w_{{\mathsf{a}}{\mathsf{a}}})]}{\overline{{W}}}}
| |
| </math>
| |
|
| |
| 采用相同方法可推导出<math display="inline">\varDelta q</math>的表达式
| |
|
| |
| <span id="自然选择对双等位基因位点的一般结果"></span>
| |
| ==== 6.2 自然选择对双等位基因位点的一般结果 ====
| |
|
| |
| 对隐性表型的选择。对显性表型的选择。显性的一般效应。<br />
| |
| • 杂合体劣势与优势。<br />
| |
| 自然选择的强度。
| |
|
| |
| 前一节展示了自然选择通过基因型特异性生存力作用于双等位基因位点的基本模型构件。本节将介绍这一基础模型下自然选择的一般结果。该任务比表面看来更简单,因为所有选择模型的结果均可表示为三类基因型的五种适应度值通用类别(表6.4)。注意表6.4以选择系数而非相对适应度表示适应度值。选择系数即相对适应度值与1的差值:
| |
|
| |
| <math display="block">
| |
| s_{x x}=1-w_{x x}\quad\text{或}\quad w_{x x}=1-s_{x x}
| |
| </math>
| |
|
| |
| 其中下标xx代表基因型,且最大相对适应度为1。因此,选择系数表示给定基因型与最高生存力基因型之间的生存力差异。
| |
|
| |
| 通过检查每类适应度值或选择系数的选择结果,可以说明生存力选择预期如何改变群体中的基因型和等位基因频率。通过对所有三种基因型迭代式6.14的不同版本,以及式6.21和6.22,我们可以可视化自然选择的作用。通过绘制等位基因频率随时间变化的图表以观察频率变化的方向和速率,可以理解自然选择下等位基因频率的行为。自然选择的一个重要普遍特征是当等位基因频率最终停止变化时达到的等位基因频率,即平衡等位基因频率。本节的目标是理解当基因型和等位基因频率受到持续自然选择作用时,其如何及为何随时间变化的机制。
| |
|
| |
| 虽然通常会说某个等位基因受自然选择青睐,但等位基因频率的任何变化实际上是由于不同存活表型导致自然选择作用于基因型的结果。在大多数类型的自然选择中(对配子或单倍体基因组的自然选择是例外),等位基因本身既没有表型也没有适合度值。基因型频率的变化才是导致等位基因频率变化的直接原因。尽管用两个等位基因频率比用三个基因型频率表示更简洁,但关键是不能忘记自然选择直接引起基因型频率的变化,而等位基因频率的变化只是间接结果。
| |
|
| |
| 自然选择过程具有一个特殊性质:只要初始频率和相对适合度值保持恒定,平衡时达到的基因型频率总是相同的。这种从给定初始条件总能导向相同结果的过程被称为确定性过程,因为最终状态完全由初始状态决定。因此,独立种群中相似的基因型频率模式可作为自然选择过程正在运作的证据。相比之下,遗传漂变的随机过程会导致每个独立种群产生随机结果。这也意味着对于相同的初始条件集,无需重复观察自然选择的结果。
| |
|
| |
| 表6.4 双等位基因位点存活选择中相对适合度值的通用分类。变量s和t用于表示基因型存活率相对于最大适合度(1)的降低量(<math display="inline">1-W_{\times\times}=s</math>)。A等位基因的显性程度用<math display="inline">h</math>表示,当<math display="inline">h=1/2</math>时表现为加性基因作用(有时称为”共显性”)。
| |
|
| |
| {|
| |
| !width="36%"| 类别
| |
| !width="36%"| 基因型特异性适合度
| |
| !width="13%"|
| |
| !width="13%"|
| |
| |-
| |
| |
| |
| | <math display="inline">W_{AA}</math>
| |
| | <math display="inline">W_{Aa}</math>
| |
| | <math display="inline">W_{aa}</math>
| |
| |-
| |
| | 对隐性表型的选择
| |
| | 1
| |
| | 1
| |
| | 1-s
| |
| |-
| |
| | 对显性表型的选择
| |
| | 1-s
| |
| | 1-s
| |
| | 1
| |
| |-
| |
| | 一般显性(显性系数0≤h≤1)
| |
| | 1
| |
| | 1-hs
| |
| | 1-s
| |
| |-
| |
| | 杂合子劣势(适合度亚显性)
| |
| | 1
| |
| | 1-s
| |
| | 1
| |
| |-
| |
| | 杂合子优势(适合度超显性)
| |
| | 1-s
| |
| | 1
| |
| | 1-t
| |
| |}
| |
|
| |
| 存活率。同时,显性纯合子(AA)的频率因其更高的存活率而增加。尽管杂合子也具有最大适合度,但随着A等位基因频率升高而a等位基因频率降低,其频率从最大值0.5逐渐下降,导致<math display="inline">2pq</math>值减小。下图通过五种初始等位基因频率随时间变化的情况,总结了自然选择对等位基因频率的影响结果(与上图中基因型频率对应的等位基因频率轨迹用彩色虚线标出)。
| |
|
| |
| ==== 对隐性表型的选择 ====
| |
|
| |
| 对完全隐性纯合基因型(见表6.4)施加自然选择作用的结果如图6.4所示。顶图展示了从初始等位基因频率<math display="inline">p=q=0.5</math>开始,三种基因型随时间变化的频率。隐性纯合子(''aa'')的频率下降是因为该基因型具有较低的适合度。
| |
|
| |
| 当初始等位基因频率较低时,早期世代的等位基因频率变化更快,因为受选择偏爱的显性纯合子和杂合子在种群中相对较多。即使初始显性等位基因频率为0.05时,仍有<math display="inline">9.75\%</math>(即<math display="inline">1-q^{2}</math>)的基因型是''AA''和''Aa''。随着隐性等位基因频率的降低(显性等位基因接近更高频率),世代间的等位基因频率变化逐渐减缓。例如,从初始等位基因频率0.05开始,前几代等位基因频率在短时间内变化0.1,但当隐性等位基因频率较低时则需要多代时间。这是因为随着选择改变基因型和等位基因频率,种群中隐性纯合子逐渐减少,而具有最高适合度的基因型(显性纯合子和杂合子)逐渐增多。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/67aae20cbb9435cc17ef488cda5d16b6d7d80ed816537c850fd54525ea160a36.jpg]]<br />
| |
| 图6.4 通过生存力选择【“viability selection”译为“生存力选择”】作用于表现隐性表型的''aa''基因型所引起的基因型和等位基因频率变化。顶图显示基因型频率随时间的变化,底图显示显性等位基因(''A'')的频率随时间变化。底图中的彩色虚线对应于顶图中的等位基因频率。由于自然选择引起的基因型频率变化,显性等位基因从五种初始频率开始都快速趋近于固定【“fixation”译为“固定”】。在本示例中,<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{Aa}}=1.0</math>而<math display="inline">w_{\mathrm{aa}}=0.8</math>,意味着每世代中具有''aa''基因型的个体中,预计有8个能存活繁殖,而具有''AA''或''Aa''基因型的个体中每10个有10个存活繁殖。基因型频率假设为随机交配。
| |
|
| |
| 当存在针对隐性纯合子的自然选择时,显性等位基因会达到固定吗?答案是否定的,因为杂合子的适合度等于最大适合度,且每个世代杂合子都会产生能组合形成隐性纯合子的配子。本质上,隐性等位基因由于显性作用在杂合子中受到自然选择的保护。无论针对隐性纯合子的选择系数多大,这一结论都成立。
| |
|
| |
| 量化杂合子庇护效应的一种方法是比较杂合子中隐性等位基因与纯合子中隐性等位基因的比例:
| |
|
| |
| <math display="block">
| |
| \frac{p q}{q^{2}}=\frac{p}{q}
| |
| </math>
| |
|
| |
| 其中杂合子的预期频率被加权了一半,因为每个杂合子仅含有一个隐性等位基因。当隐性等位基因的频率较低时(例如<math display="inline">q=0.05</math>),基因型频率的比例为<math display="inline">0.0475/0.0025=19</math>。这意味着在杂合子中受自然选择保护的隐性等位基因数量是纯合基因型中受自然选择影响的隐性等位基因数量的19倍。
| |
|
| |
| ==== 针对显性表型的选择 ====
| |
|
| |
| 当自然选择作用于显性纯合子(AA)和杂合子(Aa)共有的完全显性表型时(见表6.4),结果如图6.5所示。顶部面板显示了从初始等位基因频率<math display="inline">p=0.75</math>开始,三种基因型随时间变化的频率。显性纯合子(''AA'')的频率因其较低的生存力而下降,而隐性纯合子(''aa'')的频率因其较高的生存力而上升。尽管杂合子的相对适合度低于隐性纯合子,但由于两个等位基因的频率趋于相等,其频率最初仍会上升。当两个纯合子的频率均达到0.25时,杂合子频率在<math display="inline">2pq=0.5</math>处暂时达到峰值,随后随着隐性纯合子频率的持续上升和显性纯合子频率的持续下降而再次降低。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/9480c6868bb423f03c9aafa1ee1ca4da80d027fe7d7f8accf94fe3ec8556d6be.jpg]]<br />
| |
| '''图6.5''' 当自然选择作用于表现显性表型的''AA''和''Aa''基因型时,完全显性等位基因(A)的基因型和等位基因频率变化。注意:当A等位基因在群体中常见时,由于''aa''基因型频率较低,A等位基因频率的初始下降速度较慢。底部面板中的彩色虚线对应于顶部面板中的等位基因频率。在此示例中,<math display="inline">w_{\mathrm{AA}} = w_{\mathrm{Aa}} = 0.8</math>,而<math display="inline">w_{\mathrm{aa}} = 1.0</math>。基因型频率假设为随机交配。
| |
|
| |
| 图6.5的底部面板显示,在此类自然选择作用下,显性等位基因的频率逐渐趋近于0。(顶部面板对应的等位基因频率轨迹再次以彩色虚线标出。)当显性等位基因的初始频率为<math display="inline">p=0.95</math>时,仅有<math display="inline">0.25\%</math>(即<math display="inline">q^2</math>)的基因型为''aa''。这使得自然选择在改变等位基因频率时效率较低,直到隐性等位基因频率上升至足以使高适合度的''aa''基因型在群体中更为常见。初始A等位基因频率较低的轨迹变化更快,印证了这一观点。当自然选择作用于显性纯合子和杂合子时,隐性等位基因是否会固定?在这种情况下答案是肯定的,因为显性纯合子和杂合子的适合度均低于受偏好的纯合子,因此显性等位基因无法在杂合子中逃避自然选择。
| |
|
| |
| <span id="显性的一般情况general-dominance译为显性的一般情况"></span>
| |
| ==== 显性的一般情况【“General dominance”译为“显性的一般情况”】 ====
| |
|
| |
| 前两个关于自然选择针对显性和隐性表型的例子涵盖了显性的极端情况。通过引入显性系数(symbolized <math display="inline">h</math>),可以更普遍地描述显性和隐性等位基因对双等位基因位点上自然选择结果的影响。完全显性(杂合体与某一纯合体表型相同)由一个等位基因的<math display="inline">h=0</math>表示,而另一等位基因的完全显性由<math display="inline">h=1</math>表示。当杂合体表型为两个纯合体的平均值时,则<math display="inline">h=\hat{\mathsf{A}}_{}^{1}/_{2}\mathbf{a}</math>,这种情况有时称为共显性(codominance)。当显性系数<math display="inline">h=\hat{\mathsf{A}}_{\mathrm{/is}}</math>时,更描述性地称为加性基因作用(additive gene action),因为杂合体的表型是每个等位基因表型效应的总和。例如,若表型为<math display="inline">\mathrm{AA}=3</math>斑点、<math display="inline">\mathrm{Aa}=2</math>斑点和aa <math display="inline">=1</math>斑点,在加性基因作用时,A等位基因在杂合体中贡献1.5个斑点,a等位基因贡献0.5个斑点。参见表6.4并验证当<math display="inline">h=0</math>、1和1/2时杂合体的适合度。这种指定适合度的方法具有优势,可预测任何显性程度下自然选择的结果。这也有强烈的生物学动机,因为在真实种群中,等位基因通常表现出从完全显性到完全隐性的广泛显性或基因作用范围。
| |
|
| |
| 图6.6展示了三种基因作用情况下的选择结果。所有三种情况均以相同的初始等位基因频率开始,并共享相同的选择系数。然而,基因作用从完全显性到完全隐性变化,其中加性情况介于两者之间。对完全显性等位基因的自然选择结果(等位基因频率初期快速变化但从未达到固定)与对完全隐性等位基因的结果(初期等位基因频率变化缓慢,随后变化加速并最终固定)与早期例子中观察到的动态完全一致。加性基因作用的等位基因频率轨迹处于中间状态——它结合了完全显性初期等位基因频率快速变化的特点,以及完全隐性后期快速接近平衡和固定的特征。加性基因作用下达到平衡等位基因频率(固定或接近固定)的速度最快。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/156c11142e121cb0495b9f1280260b9523b92a340248efcf88b95f159bb0400c.jpg]]
| |
|
| |
| 图6.6 初始等位基因频率较低时,三种基因作用类型下等位基因频率随时间的变化。在所有三种情况下,A等位基因的平衡等位基因频率趋于固定或接近固定。在完全显性条件下,自然选择最初非常快速地增加等位基因频率。随着''aa''纯合子变得稀少,由于显性作用使自然选择无法作用于杂合子中的''a''等位基因,A等位基因向固定趋近的速度放缓。在隐性条件下,自然选择最初对隐性等位基因频率的改变非常缓慢,因为隐性纯合基因型非常罕见。随着隐性纯合子变得更多,等位基因频率增长加速。在加性基因作用下,杂合子的表型介于两种纯合子之间,因此所有基因型的生存力都存在差异。加性基因作用在整体上达到平衡等位基因频率的速度最快。显性程度由显性系数<math display="inline">h</math>表示。本示意图中,选择系数为<math display="inline">s=0.1</math>。
| |
|
| |
| 对于完全显性或隐性等位基因,自然选择无法区分三种基因型中的两种,因为它们的适合度值相同。这种适合度值的缺失如何影响自然选择取决于基因型频率。在隐性案例的早期世代,由于杂合子被自然选择淘汰且最适基因型稀少,等位基因频率变化缓慢。在显性案例的后期世代,杂合子为隐性等位基因提供了自然选择的庇护所,随着隐性纯合子变得极其稀少,等位基因频率的进一步变化减缓。相比之下,在加性基因作用下,三种基因型的适合度值均存在明确且均匀的差异。加性基因作用在随机交配下所有可能的基因型频率范围内,使边际适合度值与平均适合度值的差异达到最大。
| |
|
| |
| 基因作用是理解自然选择作用下新突变命运的重要因素。假设群体中出现一个新突变,其在纯合状态下具有较高的相对适合度。如第5章所述,任何新突变的初始频率都会很低<math display="inline">\big(\frac{1}{2N_{e}}\big)</math>。完全或接近隐性的突变在自然选择作用下需要极长时间才能增加频率。相比之下,具有相同纯合适合度且初始频率相同的完全或接近显性的突变,其频率将快速增长。图6.6中A等位基因初始频率为0.05的案例,等同于有效种群大小<math display="inline">N_{\mathrm{e}}=10</math>时的新突变。
| |
|
| |
| ==== 杂合子劣势 ====
| |
|
| |
| 当杂合子基因型具有最低相对适合度时的自然选择被称为'''歧化选择'''或'''分裂选择'''(见表6.4),其变化过程如图6.7所示。从初始等位基因频率<math display="inline">p=0.4</math>开始,上图显示了aa纯合子如何随时间推移最终达到固定。在此情况下需特别注意下图,因为平衡等位基因频率强烈依赖于种群初始等位基因频率。初始等位基因频率高于<math display="inline">p=0.5</math>将导致AA纯合子固定,而初始频率低于<math display="inline">p=0.5</math>将导致aa纯合子固定。当种群初始等位基因频率恰好为<math display="inline">p=0.5</math>时,等位基因频率随时间保持恒定。结果表明,这一平衡点对等位基因频率的任何变化都不具鲁棒性,因此被称为'''不稳定平衡'''。任何微小的等位基因频率变化都将导致其转向其他稳定的平衡点(固定或丢失)。这种不稳定平衡在有限种群中很难维持,因为即使轻微的遗传漂变也会使等位基因频率向某个稳定平衡点偏移。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/f34f3a6e45f2292284ccd9fbf39e20c8ba71ad887fb649d933d50ba1bd7b81fd.jpg]]<br />
| |
| '''图6.7''' 当适合度存在低显性且自然选择不利于Aa基因型个体时,基因型及等位基因频率的变化。平衡等位基因频率取决于初始等位基因频率。初始频率低于0.5时种群趋向丢失,高于0.5时趋向固定。初始等位基因频率恰好为0.5时存在不稳定平衡。无论初始频率如何,种群杂合子频率最终趋于最小值。下图彩色虚线对应上图的等位基因频率变化。本例中<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{aa}}=1.0</math>,<math display="inline">w_{\mathrm{Aa}}=0.9</math>。基因型频率假设为随机交配。
| |
|
| |
| ==== 杂合子优势 ====
| |
|
| |
| 自然选择作用导致杂合子基因型频率增加的结果(通常称为'''杂合子优势'''、'''适合度超显性'''或'''平衡选择''',见表6.4)如图6.8所示。上图显示了从初始等位基因频率<math display="inline">p=0.05</math>开始,三种基因型随时间变化的频率。由于较高的相对适合度,杂合子基因型频率增加。与此同时,aa纯合子(初始占种群的90%)因其较低生存力而减少。尽管AA纯合子的相对适合度低于杂合子,但随着等位基因频率因杂合子增加而趋近<math display="inline">p=q=0.5</math>,其频率逐渐上升至25%。下图表明,对于所有初始等位基因频率,自然选择都会使种群趋近<math display="inline">p=q=0.5</math>。
| |
|
| |
| '''适合度的超显性'''代表了对双等位基因座上自然选择结果的一个独特例外。对显性表型的选择导致隐性等位的固定和显性等位的丢失。类似地,对隐性表型的选择导致显性等位的近乎固定和隐性等位的近乎丢失。对杂合子的选择最终也会导致一个等位的固定和另一个等位的丢失。这三种形式的自然选择都会产生一个遗传变异极少或没有的平衡状态,称为'''单态平衡'''。相反,当杂合子具有最高适合度时,自然选择在平衡状态下维持种群中的两个等位,从而形成
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/62451131f6115fc673386c127c806eaba0869b55abf883acd304c241b82c6f8e.jpg]]<br />
| |
| '''图6.8''' 当存在适合度超显性且自然选择偏好具有''Aa''基因型的个体时,基因型和等位频率的变化。从任何初始等位频率出发,种群会收敛于杂合子的最大频率。这对应于随机交配下等位频率相等的状态。下图中的彩色虚线对应于上图中等位频率的变化。在此示例中,<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{aa}}=0.9</math>且<math display="inline">w_{\mathrm{Aa}}=1.0\AA</math>。基因型频率假设为随机交配。
| |
|
| |
| 的'''多态平衡'''。因此,适合度的超显性是自然选择的一种类型,与种群中遗传变异的永久维持相一致。
| |
|
| |
| 超显性下的平衡等位频率可通过'''公式6.23'''(如数学框6.2所示)计算得出。平衡等位频率为:
| |
|
| |
| <math display="block">
| |
| p_{equilibrium}=\frac{t}{s+t}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| q_{equilibrium}=\frac{s}{s+t}
| |
| </math>
| |
|
| |
| 其中<math display="inline">s</math>和<math display="inline">t</math>分别为针对''AA''和''aa''纯合子的选择系数(见表6.4)。在纯合基因型中具有较小选择系数(或较高相对适合度)的等位,其平衡频率更高。
| |
|
| |
| <span id="math-box-6.2-超显性下的平衡等位频率"></span>
| |
| = Math Box 6.2 超显性下的平衡等位频率 =
| |
|
| |
| 根据定义,当等位频率在世代间停止变化时,即达到平衡等位频率。这意味着如'''公式6.23'''所表达的<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>:
| |
|
| |
| <math display="block">
| |
| \hat{\mathbf{\omega}}^{\prime\prime}p=\frac{p q[p(w_{\mathsf{A A}}-w_{\mathsf{A a}})+q(w_{\mathsf{A a}}-w_{\mathsf{a a}})]}{\overline{{W}}}
| |
| </math>
| |
|
| |
| 应等于0。
| |
|
| |
| 当<math display="inline">p=0</math>或<math display="inline">q=0</math>时存在两个平衡点,生物学上等同于种群中无遗传变异的情况。当存在遗传变异(即<math display="inline">p\neq0</math>且<math display="inline">q\neq0</math>)时,平衡点取决于分子中的适合度差异。将'''公式6.37'''中方括号内的分子项设为0:
| |
|
| |
| <math display="block">
| |
| p(w_{\mathsf{A A}}-w_{\mathsf{A}\mathsf{a}})+q(w_{\mathsf{A}\mathsf{a}}-w_{\mathsf{a}\mathsf{a}}})=0
| |
| </math>
| |
|
| |
| 然后以相对适合度值求解<math display="inline">p</math>或<math display="inline">q</math>,即可得到<math display="inline">\hat{\mathsf{I}}^{\prime\prime}q</math>为0的等位频率。第一步是代入<math display="inline">q=1-p</math>:
| |
|
| |
| $$
| |
|
| |
| p(w_{}-w_{})+(1-p)(w_{}-w_{})=0 $$
| |
|
| |
| 然后将各项展开相乘
| |
|
| |
| <math display="block">
| |
| p w_{\mathsf{A A}}-p w_{\mathsf{A}a}+w_{\mathsf{A}a}-w_{\mathsf{a}a}-p w_{\mathsf{A}a}+p w_{\mathsf{a}a}=0
| |
| </math>
| |
|
| |
| 将乘以<math display="inline">p</math>的相对适合度项合并
| |
|
| |
| <math display="block">
| |
| p(w_{\mathsf{A A}}-2w_{\mathsf{A}a}+w_{\mathsf{a}a})+w_{\mathsf{A}a}-w_{\mathsf{a}a}=0
| |
| </math>
| |
|
| |
| 然后移项
| |
|
| |
| <math display="block">
| |
| w_{\mathsf{A}a}-w_{\mathsf{a}a}=-p(w_{\mathsf{A}\mathsf{A}}-2w_{\mathsf{A}a}+w_{\mathsf{a}a})
| |
| </math>
| |
|
| |
| 两边同除以<math display="inline">-(w_{\mathsf{A A}}-2w_{\mathsf{A}a}+w_{\mathsf{a}a})</math>得
| |
|
| |
| <math display="block">
| |
| p=\frac{W_{\mathsf{A}a}-W_{\mathsf{a}a}}{2W_{\mathsf{A}a}-W_{\mathsf{A}\mathsf{A}}-W_{\mathsf{a}a}}
| |
| </math>
| |
|
| |
| 这表示<math display="inline">p</math>仅作为相对适合度值的函数。将表6.4中给出的相对适合度值<math display="inline">w_{\mathsf{A A}}=1-\varsigma,w_{\mathsf{A}a}=1.</math>和<math display="inline">w_{\tt a a}=1-t</math>代入:
| |
|
| |
| <math display="block">
| |
| p=\frac{1-(1-t)}{2(1)-(1-s)-(1-t)}
| |
| </math>
| |
|
| |
| 通过加减运算最终得到用两个纯合基因型选择系数表示的等位基因平衡频率
| |
|
| |
| <math display="block">
| |
| p={\frac{t}{s+t}}
| |
| </math>
| |
|
| |
| ==== 自然选择的强度 ====
| |
|
| |
| 对某一基因型的选择强度可以从非常弱(如生存力比最适基因型低<math display="inline">0.1\%</math>)到非常强(如基因型生存力为<math display="inline">50\%</math>甚至完全致死)。图6.9展示了在针对隐性纯合基因型的自然选择中,不同选择系数下等位基因频率随时间的变化(起始频率相同)。注意图6.9上下两版中曲线形态非常相似,但每个图的时间尺度差异显著。当选择系数为<math display="inline">10\%</math>或更大时,显性等位基因在100代内即可达到高频率;而当选择系数在<math display="inline">1.0\%</math>至<math display="inline">0.1\%</math>之间时,达到相同频率需要10 000代。这验证了普遍原理:更强的自然选择(更大的选择系数或更大的适合度差异)会导致等位基因频率更快趋近平衡状态。该结论适用于表6.4列出的所有情况,也普遍适用于自然选择过程。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/c65786fe429913a14129558a8a0372a267968bace56a0cd24d6bfe709f395dfd.jpg]]<br />
| |
| 图6.9 自然选择强度影响基因型和等位基因频率的变化速率。本示意图中,选择作用于隐性纯合体(aa)。上版显示强自然选择,aa基因型的生存力比其他基因型低<math display="inline">10\hat{\mathsf{a}}\hat{\mathsf{E}}0\%</math>;下版显示弱自然选择,aa基因型的生存力比其他基因型低<math display="inline">1\hat{\mathsf{a}}\hat{\mathsf{e}}{\cdot}1\%</math>。注意两图的时间尺度差异巨大。
| |
|
| |
| <span id="自然选择如何提高平均适合度"></span>
| |
| ==== 6.3 自然选择如何提高平均适合度 ====
| |
|
| |
| aE自然选择通过提高平均适合度发挥作用。<br />
| |
| aE自然选择基本定理。
| |
|
| |
| 在表6.4所示的五种关于双等位基因座自然选择的相对适合度情形中,始终存在两种一般结果。任何类型的定向选择最终都会导致固定和丢失(针对显性表型的选择)或接近固定和丢失(针对隐性表型的选择)。欠显性也会导致固定或丢失(在有限种群中几乎不可能实现的一个例外情况)。过显性则是例外,它使两个等位基因在种群中无限期共存。因此,两种结果要么是等位基因的固定与丢失,要么是两者保持中等频率(有时称为平衡多态性)。通过考察种群的平均适合度<math display="inline">(\overline{\mathbf{w}})</math>以及等位基因频率在整个范围内的变化速率<math display="inline">(\Delta p)</math>,可以理解这两种一般结果出现的原因。
| |
|
| |
| ==== 平均适合度与等位基因频率变化速率 ====
| |
|
| |
| 图6.10和6.11绘制了双等位基因座自然选择各情形下所有可能等位基因频率对应的平均适合度(<math display="inline">\overline{w}</math>)。对于图6.10中定向选择的案例,值得注意的是:在针对隐性表型的选择中,最高平均适合度恰好对应A等位基因的固定;而在针对显性表型的选择中,最高平均适合度对应A等位基因的丢失。这一模式在图6.11中同样明显——过显性情形下最高平均适合度出现在中等等位基因频率处,而欠显性情形下则出现在固定或丢失状态。
| |
|
| |
| 通过等位基因频率绘制的平均适合度曲线表明,自然选择的作用是使种群的平均适合度增至最大值。种群中最大平均适合度实际上定义了基因型和等位基因频率的平衡点。<math display="inline">\overline{w}</math>随<math display="inline">p</math>变化的曲线揭示了一个普遍规律:自然选择过程在每一世代都尽可能地提高种群平均适合度,并在平均适合度无法继续提高时停止。从这个意义上说,自然选择可以隐喻为一位不断寻找最高点、永不向下、只在顶峰停留的登山者。沿用这个隐喻,<math display="inline">\overline{W}</math>随<math display="inline">p</math>变化的曲线被称为适合度曲面、适应景观或适应地形图,它们构成了这位想象中登山者可能涉足区域的等高线地图。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/0a7e3277162621aea7ae932269a0bac5bf31b897fe94723078f10438b877697d.jpg]]
| |
|
| |
| 【“adaptive topographies”译为“适应地形图”】
| |
|
| |
| 图6.1o 定向选择下群体平均适合度(w)和单世代内等位基因频率变化<math display="inline">(\hat{\mathsf{I}}^{\prime\prime}p)</math>随等位基因频率的变化关系。定向选择使等位基因频率在固定或丢失时达到平衡,即平均适合度最高的点。<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>的正值(虚线以上)表示选择作用下等位基因频率在增加,而<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>的负值(虚线以下)表示选择作用下等位基因频率在减少。当平均适合度变化更快时(w的斜率更陡),等位基因频率的变化也更快。此处,针对隐性表型的选择参数为<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{Aa}}=1.0</math>和<math display="inline">w_{\mathrm{aa}}=0.8</math>,针对显性表型的选择参数为<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{Aa}}=0.8</math>和<math display="inline">w_{\mathrm{aa}}=1.0</math>。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/42b3017e372ff94729f8949cb2313224c9ff3175818b10d8c65127cf67807832.jpg]]<br />
| |
| 图6.11 平衡选择和分裂选择下群体平均适合度(w)与单世代内等位基因频率变化<math display="inline">(\hat{\mathsf{I}}^{\prime\prime}p)</math>随等位基因频率的变化关系。自然选择通过改变等位基因频率使每代平均适合度增加,最终在平均适合度最高时达到平衡。当平均适合度变化更快时(w的斜率更陡),等位基因频率的变化也更快。图中<math display="inline">\tilde{|^{\eta}}_{p}</math>随p变化的虚线标明了等位基因频率停止变化的位置<math display="inline">(\hat{\ l}^{\prime\prime}p=\stackrel{\smile}{0})</math>,即等位基因频率平衡点。在适合度显性不足时,<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>在<math display="inline">p=0.5</math>处为零(圆圈标记),但该平衡点不稳定——<math display="inline">p=0.5</math>两侧的<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>会使等位基因频率远离平衡点(<math display="inline">\bar{p}=0.5\widehat{|^{\prime}p}</math>下方为负值导致等位基因丢失,<math display="inline">\overset{\cdot}{p}=0.5\hat{\overset{\cdot}{\vert}}\overset{\eta}{p}</math>上方为正值导致等位基因固定)。相反,在超显性时,<math display="inline">p=0.5</math>两侧的<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>会使等位基因频率趋向平衡点(<math display="inline">p=0.5\hat{\mathsf{l}}^{\prime\prime}p</math>下方为正值,上方为负值),因此<math display="inline">p=0.5</math>是稳定平衡点。此处,显性不足的参数为<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{aa}}=1.0</math>和<math display="inline">w_{\mathrm{Aa}}=0.7</math>,超显性的参数为<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{aa}}=0.7</math>和<math display="inline">w_{\mathrm{Aa}}=1.0</math>。
| |
|
| |
| 图6.10和6.11还展示了每种自然选择情况下,单一代内等位基因频率变化(Δ''p'')在所有可能等位基因频率上的分布。Δ''p''对''p''的作图揭示了等位基因频率何时在增加(Δ''p''为正)、减少(Δ''p''为负)、快速变化(Δ''p''绝对值大)或缓慢变化(Δ''p''绝对值小)。当等位基因频率完全不变化时(Δ''p''=0),即达到了平衡等位基因频率。
| |
|
| |
| 注意在定向选择中,A等位基因的固定或丢失对应于Δ''p''=0。对于overdominance和underdominance,Δ''p''=0的情况不仅出现在固定和丢失时,也出现在中间等位基因频率''p''=0.5处。这些等位基因频率因此成为平衡点,因为自然选择在这些特定频率下不会引起任何变化。
| |
|
| |
| 此外,将每个Δ''p''对''p''的作图与对应的''W̄''对''p''的作图进行比较时,可以发现Δ''p''与''W̄''之间存在显著关系。Δ''p''的大小和符号精确对应于''W̄''曲线在任意''p''值处的斜率。例如:当选择作用于隐性不利时,''W̄''的斜率始终为正,正如Δ''p''始终为正;当选择作用于显性不利时,''W̄''的斜率始终为负,正如Δ''p''始终为负(图6.10)。
| |
|
| |
| 这种模式同样体现在图6.11的overdominance和underdominance案例中:''W̄''的斜率在固定、丢失以及''p''=0.5处均为0。''W̄''的斜率解释了为何overdominance的多态平衡点是稳定的,而underdominance的平衡点是不稳定的。
| |
|
| |
| 在overdominance情况下,若等位基因频率因遗传漂变或突变偏离''p''=0.5,自然选择将使种群回到''p''=0.5的平衡(当''p''<0.5时Δ''p''为正,''p''>0.5时Δ''p''为负)。相反,在underdominance情况下,任何偏离''p''=0.5的等位基因频率变化都会被自然选择推向固定或丢失处的最大平均适合度值(当''p''<0.5时Δ''p''为负,''p''>0.5时Δ''p''为正)。
| |
|
| |
| <span id="problem-box-6.2-平均适合度与等位基因频率变化"></span>
| |
| = Problem box 6.2 平均适合度与等位基因频率变化 =
| |
|
| |
| 使用式6.35和6.36可以预测适合度超显性选择下的平衡等位基因频率。我们还需要理解为什么平衡点是基因型频率停止变化的点。假设适合度值为<math display="inline">W_{\mathrm{AA}}=0.9</math>,<math display="inline">w_{\mathsf{A a}}=1.0</math>,<math display="inline">w_{\tt a a}=0.8</math>。首先计算平衡时A等位基因的预期频率或Pequilibrium。接着在<math display="inline">p=0.9</math>和<math display="inline">p=0.2</math>时计算<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>和平均适合度<math display="inline">\overline{{W}}</math>。这三个等位基因频率下的<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>和<math display="inline">\overline{{W}}</math>值如何比较?用<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>和<math display="inline">\overline{{W}}</math>解释为什么平衡等位基因频率位于<math display="inline">p=0.9</math>和<math display="inline">p=0.2</math>之间。
| |
|
| |
| <span id="互动框6.1-双等位基因位点的自然选择"></span>
| |
| = 互动框6.1 双等位基因位点的自然选择 =
| |
|
| |
| 使用文本模拟网站进行自然选择模拟(在模拟菜单中选择双等位基因位点的自然选择)。设置AA和Aa基因型的初始频率以及所有三种基因型的相对适合度值。对于每组适合度值,请确保至少模拟四个初始等位基因频率,以理解结果如何依赖初始条件(如图6.4、6.5、6.7和6.8的底部面板)。
| |
|
| |
| 以下是模拟中可使用的适合度值:
| |
|
| |
| • 对隐性基因的弱选择:<math display="inline">W_{\mathrm{AA}}=1</math>;<math display="inline">W_{\mathrm{Aa}}=1</math>;<math display="inline">{\cal W}_{\tt a a}=0.9</math>(<math display="inline">h=0,s=0.1^{\cdot}</math>)。与隐性致死选择比较:<math display="inline">W_{\mathrm{AA}}=1</math>;<math display="inline">W_{\mathrm{Aa}}=\mathbb{1}</math>;<math display="inline">w_{\tt a a}=0.0</math>(<math display="inline">\mathit{\Theta}_{\mathit{h}}=0</math>,<math display="inline">s=1.0</math>) • 加性基因作用的弱选择:<math display="inline">W_{\mathrm{AA}}=1</math>;<math display="inline">W_{\mathrm{{Aa}}}=0.95</math>;<math display="inline">{\cal W}_{\tt a a}=0.9</math>(<math display="inline">h=0.5</math>,<math display="inline">s=0.1</math>)。与加性基因作用的强选择比较:<math display="inline">W_{\mathsf{A A}}=1</math>;<math display="inline">w_{\mathsf{A}a}=0.7</math>;<math display="inline">w_{\mathsf{a}a}=0.4</math>(<math display="inline">h=0.5,s=0.6</math>) • 超显性的弱选择:<math display="inline">w_{\mathsf{A A}}=0.98</math>;<math display="inline">W_{\mathrm{Aa}}=1</math>;<math display="inline">W_{\mathrm{aa}}=0.95</math>。与超显性的强选择比较:<math display="inline">{w_{\mathsf{A A}}}=0.2</math>;<math display="inline">W_{\mathrm{Aa}}=1</math>;<math display="inline">W_{\mathrm{aa}}=0.4</math> • 针对杂合子的选择:<math display="inline">W_{\mathsf{A A}}=1</math>;<math display="inline">W_{\mathsf{A a}}=0.8</math>;<math display="inline">W_{\mathsf{a a}}=1</math>。对于这种情况,请确保检查多个初始等位基因频率(如0.2、0.5和0.8)的轨迹图。
| |
|
| |
| ==== 自然选择的基本定理 ====
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/c2886b73270c176ed09646bd3a02214f96c6f367aacc51f0949bde023e0d1a82.jpg]]<br />
| |
| 图6.12 罗纳德·A·费舍尔爵士(1890-1962)摄于1943年,是统计学理论与实践的先驱。他发明了方差分析和极大似然法技术,以及众多其他统计检验方法和实验设计方法。费舍尔1930年著作《自然选择的遗传理论》建立了将孟德尔遗传与达尔文定性自然选择模型相结合的严格数学框架,是现代群体遗传学的奠基之作。费舍尔的大部分工作强调了自然选择在无限随机交配群体中改变基因频率的有效性。来源:Anthony W.F. Edwards,冈维尔与凯斯学院院长及院士,剑桥大学。
| |
|
| |
| 阐释基本定理思想的一种方法是考察自然选择与群体平均适合度随时间的变化。为简化起见,假设生物体完全为单倍体并通过无性繁殖或克隆繁殖,且世代离散(这些假设并非基本定理本身所必需,但可使数学处理大为简化)。在单倍体情形下,平均适合度是各单体型适合度按其频率加权后的总和(回顾式6.10)。用方程表示,平均适合度为:
| |
|
| |
| <math display="block">
| |
| \overline{w}=\sum_{i=1}^{k}(p_{i}w_{i})
| |
| </math>
| |
|
| |
| 其中<math display="inline">k</math>是群体中单体型的总数。将表6.1的结果推广到任意等位基因数,经自然选择后任一单体型(记作第<math display="inline">i</math>号单体型)的频率为:
| |
|
| |
| <math display="block">
| |
| p_{i}^{\prime}={\frac{p_{i}w_{i}}{\overline{w}}}
| |
| </math>
| |
|
| |
| 其中撇号用于表示经历一代自然选择后的量。基于选择后的单体型频率,经历一代选择后的平均适合度则为:
| |
|
| |
| <math display="block">
| |
| \overline{w}^{\prime}=\sum_{i=1}^{k}(p_{i}^{\prime}w_{i})
| |
| </math>
| |
|
| |
| 将式6.47中<math display="inline">p_i^{\prime}</math>的表达式代入后可得:
| |
|
| |
| <math display="block">
| |
| \overline{w}^{\prime}=\frac{1}{\overline{w}}\sum_{i=1}^{k}p_{i}w_{i}^{2}
| |
| </math>
| |
|
| |
| 下一代适应度的变化,以初始世代的平均适应度标准化后为
| |
|
| |
| <math display="block">
| |
| \widehat{\sf I}^{\prime\prime}\overline{{\sf w}}=\frac{\overline{{\sf w}}^{\prime}-\overline{{\sf w}}}{\overline{{\sf w}}}
| |
| </math>
| |
|
| |
| 将其代入式6.49中关于<math display="inline">\overrightarrow{W}</math>的表达式可得
| |
|
| |
| <math display="block">
| |
| \hat{\mathsf{I}}^{\prime\prime}\overline{{\boldsymbol{w}}}=\frac{\frac{1}{\overline{{w}}}\displaystyle\sum_{i=1}^{k}p_{i}w_{i}^{2}-\overline{{w}}}{\overline{{w}}}
| |
| </math>
| |
|
| |
| 该方程可通过乘以<math display="inline">\frac{1}{\overline{{\mathbf{w}}}}</math>而非除以<math display="inline">\overline{{w}}</math>重新整理为
| |
|
| |
| <math display="block">
| |
| {\widehat{\sf w}}^{\prime\prime}{\overline{{\sf w}}}={\frac{1}{\overline{{\boldsymbol{w}}}}}\left[{\frac{1}{\overline{{\boldsymbol{w}}}}}\sum_{i=1}^{k}p_{i}\boldsymbol{w}_{i}^{2}-\overline{{\boldsymbol{w}}}\right]={\frac{1}{\overline{{\boldsymbol{w}}}^{2}}}\sum_{i=1}^{k}p_{i}\boldsymbol{w}_{i}^{2}-{\frac{\overline{{\boldsymbol{w}}}}{\overline{{\boldsymbol{w}}}}}
| |
| </math>
| |
|
| |
| 事实上,当所有单倍型的相对适应度值被缩放至<math display="inline">\overline{{w}}=1</math>时,项<math display="inline">\sum_{i=1}^{k}p_{i}w_{i}^{2}-1</math>即为适应度的方差(方差定义为<math display="inline">\sum\left(p_{i}w_{i}-{\overline{{w}}}\right)^{2}</math>,等价于<math display="inline">\sum p_{i}w_{i}^{2}-\overline{{w}}^{2}~)</math>。当所有单倍型的相对适应度值被缩放至<math display="inline">\overline{{\mathrm{~w~}}}=1</math>时,可得
| |
|
| |
| <math display="block">
| |
| \widehat{\sf I}^{\prime\prime}\overline{{\boldsymbol{w}}}=\boldsymbol{\mathrm{var}}(\boldsymbol{\mathrm{w}})
| |
| </math>
| |
|
| |
| 由此得出结论:经过一代自然选择后种群平均适应度的变化等于适应度的方差。在单倍体情况下,这种适应度变异本质上是遗传变异,源于种群中不同单倍型的频率差异及各单倍型适应度值的差异。因此,自然选择下的适应度变化等于适应度的遗传变异。此外,由于方差永不为负,自然选择引起的平均适应度变化必定大于或等于零。
| |
|
| |
| FisheraefMndamental定理【“FisheraefMndamental theorem”译为“费希尔基本定理”】的要点也可通过de Finetti图(第二章介绍)在二倍体双等位基因位点中图示展现,该图同时呈现种群的适应度均值(图6.13)。具体而言,令2Q、P和<math display="inline">R</math>分别表示基因型Aa、AA和aa的频率。基因型频率的比值可表示为杂合子频率平方的一半除以纯合子频率的乘积,即<math display="inline">\hat{\mathsf{I}}_{\mathsf{N}}^{*}=\mathsf{Q}^{2}/\hat{P R}</math>↑>,该指标类似于固定指数F,用于衡量与HardyaWeinberg基因型频率的偏离程度。当基因型频率符合HardyaWreinberg比例时,基因型频率为<math display="inline">2Q=2p q</math>、<math display="inline">P={p^{2}}</math>、<math display="inline">R=\boldsymbol q^{2}</math>,且<math display="inline">\hat{\uparrow}_{\gg=1}</math>。图6.13中两条虚线对应的λ值小于1。图6.13中de Finetti图的每个点还代表种群适应度的均值,具体取决于各基因型相对适应度值。de Finetti图上的平均适应度以灰度梯度表示,色调越深代表平均适应度越高。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/9a7b2b71ce323443ce4d4fce2dde471a725537df1fe515f45e8ea7a70d237f9d.jpg]]<br />
| |
| 图6.13 R.A. Fisher自然选择基本定理的图示说明。曲线表示纯合子频率的乘积(<math display="inline">P=p^{2}</math>和<math display="inline">R=q^{2}</math>)作为等位基因频率乘积平方(<math display="inline">Q=pq</math>或<math display="inline">\hat{\mathsf{I}}{\ast}{=}Q^{2}/PR</math>)的恒定比例。随机交配产生的Hardy-Weinberg基因型频率代表<math display="inline">\hat{\mathsf{I}}_{\gg}\stackrel{}{=}1</math>的特殊情况(实色线)。平均适应度以灰度梯度表示,色调越深代表平均适应度越高。在此图示中,基因型频率起始于<math display="inline">z_{1}</math>。假设自然选择在一代中将基因型频率改变至点<math display="inline">z_{3}</math>(例如在基因型AA具有最高适应度和加性基因作用【“additive gene action”译为”加性基因作用”】的条件下)。这种基因型频率变化可分解为两个独立部分:第一部分是从<math display="inline">z_{1}</math>到<math display="inline">z_{2}</math>沿着λ值恒定曲线的变化,此时等位基因频率从<math display="inline">p</math>变为<math display="inline">p\hat{\mathsf{a}}\hat{\mathsf{e}}\mathtt{M e}</math>;第二部分是通过在de Finetti图上垂直移动从<math display="inline">z_{2}</math>到<math display="inline">z_{3}</math>的基因型频率变化(改变<math display="inline">\hat{\vert\cdot\rangle}</math>值)但保持等位基因频率不变。基本定理指出,自然选择引起的平均适应度变化仅与等位基因频率变化成比例。交配系统等非自然选择过程主导基因型频率的变化。当自然选择使基因型频率沿恒定λ曲线移动时,平均适应度的总变化完全源于等位基因频率变化,且适应度的遗传变异完全为加性。来源:修改自Edwards(2002)。
| |
|
| |
| 自然选择下平均适应度的变化可以视为在德菲内蒂图(de Finetti diagram,Edwards 2002)上的两步过程。第一步中,等位基因频率从当前值变化到新值,同时保持基因型频率的比例不变。这相当于从点<math display="inline">z_{1}</math>移动到点<math display="inline">z_{2}</math>,同时保持在定义恒定λ值的直线上。第二步中,种群通过改变基因型频率(但不改变等位基因频率)从点<math display="inline">z_{2}</math>移动到点<math display="inline">z_{3}</math>。由选择引起的平均适应度变化的第一部分仅源于等位基因频率的变化,而其他所有因素保持恒定。这种完全由等位基因频率变化引起的平均适应度的部分变化,与种群在点<math display="inline">z_{1}</math>时存在的基因方差(genic variance)或加性遗传方差(additive genetic variance)完全相同。平均适应度变化的第二部分源于基因型频率的变化,因此由交配模式或物理连锁(physical linkage)等因素引起,这些因素会导致配子不平衡(gametic disequilibrium),从而在等位基因频率变化时改变λ值。基本定理指出,自然选择将仅通过加性遗传方差的比例来改变平均适应度。如果λ保持恒定,平均适应度的总变化仅由等位基因频率的变异引起。当λ不恒定时,基因型频率的变化可能增加或减少平均适应度,并可视为导致平均变化为零。
| |
|
| |
| 由等位基因替换(加性遗传变异)和基因型效应引起的表型遗传变异,将在第9章和第10章定量遗传学中以完全不同的视角进行探讨。这些章节也阐明了基本定理中对等位基因频率变化引起的遗传变异与基因型频率变化引起的遗传变异的区分。两种方法均得出相同结论:加性遗传变异是自然选择导致表型均值变化的基础。
| |
|
| |
| <span id="自然选择的单一位点双等位基因模型的意义"></span>
| |
| ==== 6.4 自然选择的单一位点双等位基因模型的意义 ====
| |
|
| |
| • 古典假说与平衡假说。<br />
| |
| aE 如何解释同工酶多态性(allozyme polymorphism)的水平。
| |
|
| |
| Fisher、Haldane和Wright的理论工作确立了群体遗传学的核心原理。这些成果包括本章描述的自然选择单一位点双等位基因模型,以及关于突变和重组如何提供遗传变异的预测、交配模式和基因流对遗传变异等级结构的影响,以及有效种群大小(effective population size)如何调控遗传漂变(genetic drift)过程的结论。整体而言,这套理论预期将达尔文的自然选择概念与孟德尔颗粒遗传(Mendelian particulate inheritance)原理相融合。这些预期构成了群体遗传学的基础,并被Huxley(1942)称为新达尔文主义(neo-Darwinism)。
| |
|
| |
| <span id="the-classical-and-balance-hypotheses"></span>
| |
| ==== The Classical and Balance Hypotheses ====
| |
|
| |
| Whereas the neo-Darwinian synthesis achieved by population genetics reached orthodoxy in the 1930s and 1940s, a long-running debate began to take shape. Under the logic of early neo-Darwinism, natural selection was the dominant evolutionary force in almost all aspects of evolutionary change. It was then a matter of debate as to what type of natural selection – directional, stabilizing, or disruptive – was most common in captive and natural populations. The answer to this question gradually turned into two broad points of view based on what one assumed and how one interpreted available data on genetic variation. Dobzhansky (1955) labeled these schools of thought the classical hypothesis and the balance hypothesis. Both hypotheses rely on natural selection as the principle process operating in populations, although they differ greatly in the predicted consequences.
| |
|
| |
| <span id="classical-hypothesis"></span>
| |
| === Classical hypothesis ===
| |
|
| |
| The point of view that directional natural selection is the dominant process in populations, predicting relatively little genetic variation except when selection pressures are heterogeneous in time or space or are frequency-dependent.
| |
|
| |
| <span id="balance-hypothesis"></span>
| |
| === Balance hypothesis ===
| |
|
| |
| The point of view that balancing natural selection is the dominant process in populations, predicting extensive genetic variation caused by overdominance for fitness.
| |
|
| |
| The classical hypothesis was that directional selection was the predominant process in populations, and from this, two major predictions arise as a consequence. The first prediction was that, under random mating, populations contained individuals homozygous at most loci. The second prediction was that populations harbored relatively little genetic variation since the equilibrium points for any sort of directional selection on a diallelic locus are fixation and loss or near fixation and loss. The classical school recognized the existence of ''adeltypealleles'', or alleles at high frequency in a population because such alleles were of higher fitness and were brought to high frequency by directional selection. Alternative ''aoantaelleles'' that appeared in populations were most often deleterious but on very rare occasions would have a higher fitness than the current wild-type allele and would then become the new wild-type allele.
| |
|
| |
| The classical school predictions were supported by a range of empirical observations, especially from laboratory populations of organisms such as ''Drosophila''. In such populations, phenotypes are of the wild type (within some range of variation) and mutations with visible phenotypic effects appear rarely but are almost universally deleterious and do not reach high frequencies.
| |
|
| |
| 【“adeltypealleles”译为“优势型等位基因”】<br />
| |
| 【“aoantaelleles”译为“替代型等位基因”】
| |
|
| |
| 经典假说预测,群体中的遗传变异通过四种方式产生(Dobzhansky 1955)。第一,有害突变持续发生并在被定向自然选择清除前短暂分离。这些有害突变大多可能是隐性突变,因此主要存在于杂合子基因型中,从而受到自然选择的庇护。(Dobzhansky指出这类突变在纯合状态下会导致遗传疾病。)第二,部分突变因具有接近平均适合度的边缘适合度值而呈现选择性中性。第三可能性是,在稀有有利突变成为新的野生型等位基因之前,会在群体中被发现。第四可能性是,某些突变在一种环境中略有优势,但在另一种环境中略有劣势。当群体暴露于时空异质性环境时,等位基因将因此持续存在。最后这一类别推动了大量群体遗传学模型的建立,这些模型涉及随时间或空间变化的定向选择,或个体适合度具有频率依赖性(见第7章)。
| |
|
| |
| 平衡假说则持相反观点,认为适合度的超显性在大多数群体中是普遍规律,因此平衡选择是调节遗传变异的主要过程。(注意具有稀有等位基因优势的频率依赖性选择也被视为平衡选择的一种形式,见第7章。)在平衡选择作用下,杂合子的频率会高于无选择或定向选择时的情况。因此平衡假说预测,基因座将无限期地维持两个或多个等位基因。由于平衡选择的存在,杂合子将比Hardya*einberg定律预期或在定向选择下更常见,而纯合子则远少于预期。对于进入群体的新突变,只有那些在杂合状态下表现出超显性的突变才可能被保留在群体中。
| |
|
| |
| 正如 Dobzhansky(1955)所解释的,平衡假说还与关于位点间相互关系的预测相关。对多个位点的自然选择可导致配子不平衡的积累(见第2章)。在平衡选择作用下,当群体中所有位点的等位基因频率处于中间值时,预计会出现高水平的配子不平衡,因为只有能产生多座位杂合子合子的那部分配子具有高适合度。(需注意,在经典假说框架下虽然也存在强自然选择,但预计绝对水平的配子不平衡相对较少,因为群体中野生型等位基因的频率会接近固定。)
| |
|
| |
| 利用这种对配子不平衡的预期,并假设大多数位点经历平衡选择,可推导出物种内存在共适应基因复合体或超基因的预测(Hedrick et al. 1978; Thompson and Jiggins 2014)。超基因是指多个位点上通过极强的配子不平衡而保持联结,并经常以完整单元形式遗传的单体型或基因型。共适应基因复合体是一种超基因,其自然选择作用(或曾作用)使得每个位点的等位基因或基因型与其他所有位点的等位基因或基因型在组合时具有高适合度。换言之,选择将提高那些与其他位点的等位基因和杂合基因型良好互作的新突变频率。相反,任何因位点间互作导致相对适合度降低的突变,其频率都将被自然选择降低。因此,共适应基因复合体的概念假设适合度的上位效应是普遍存在的。
| |
|
| |
| 超基因和共适应基因复合体为经典/平衡假说时期的生物学家既提供了研究议程,也带来了概念挑战。大量研究致力于实验室和自然群体中多位点遗传变异的分析。与此同时,多位点自然选择和重组的多种模型被建立和研究。由平衡选择和适合度上位效应引起的极高水平配子不平衡,实质上否定了孟德尔独立分配的机制。那么进化改变所需的遗传变异来源何在?答案常需从具有重组或分解超基因潜力的群体遗传机制中探寻。
| |
|
| |
| 关于由配子不平衡维系'''超基因'''在自然种群中普遍存在的观点,现已被视为一个连续统的极端形式。当代群体遗传学已内化了对导致配子不平衡过程的理解,并认识到多位点间并非必然独立。目前已有多个基因组区域被充分证实具有高水平配子不平衡,例如哺乳动物的'''主要组织相容性复合体'''(''Mhc'')基因座。这些基因座因在识别非自身肽段中的功能作用而经历平衡选择,构成一个具有相对高配子不平衡水平的染色体大区。超基因的预测现已细化为适用于不同情境的一系列具体假说。
| |
|
| |
| 位点的非独立性是解释种群内多态性的分子演化模型的核心,这体现于搭车效应(hitchhiking)、背景选择(background selection)和遗传漂变(genetic draft)等概念(参见第8章)。数量遗传学认识到由表型相关性和遗传相关性导致的性状非独立性。关于选择偏好多个位点间良好互作等位基因的思想,现称为'''DobzhanskyaMuller模型'''【“DobzhanskyaMuller”译为“多布然斯基-穆勒”】,该模型解释了孤立种群如何发展出生殖隔离从而导致物种形成(Coyne和Orr 2004年综述)。
| |
|
| |
| 生态遗传学研究可追溯至用实证数据检验经典假说与平衡假说的努力。如今,生态遗传学被定义为在环境变异与生物互作背景下研究物种内的遗传变异。该领域致力于识别遗传多态性模式的成因,通常涉及生态背景施加的自然选择压力(无论假设或证实)。早期生态遗传学聚焦于检验遗传变异的经典假说与平衡假说:经典学派预测基因型的相对适合度具有时空变化性;平衡学派则预测适合度超显性现象十分普遍。这两种可能性都可通过测量已知遗传基础表型的相对适合度,或观察遗传多态性频率,在自然种群中得到一定程度的检验。
| |
|
| |
| Dobzhansky是首批在野外研究akberatorya6rganisms的学者之一。他开创了果蝇属(''Drosophila'')的野外研究,奠定了当今群体遗传学实证研究的范式。Edmund B. Ford在生态遗传学领域的确立中也发挥了关键作用。Ford研究野生蝶蛾类,并撰写了1964年首版、1975年再版的影响深远的著作《Ecological Genetics》。
| |
|
| |
| ==== 如何解释同工酶多态性水平 ====
| |
|
| |
| 当通过经典假说/平衡假说辩论的视角审视时,生态遗传学中许多广为人知的实证研究获得了新的意义。例如,英国椒花蛾(''Biston betularia'')种群中的工业黑化现象为经典学派提供了证据,因为它表明定向选择压力因种群接近工业中心(其煤烟将树干染黑)而存在差异(Majerus 1998年综述)。(牛津大学研究员Bernard Kettlewell完成了大部分早期椒花蛾研究工作并非巧合,他受E.B. Ford指导。)广为人知的人类群体案例是免疫系统基因主要组织相容性复合体(MHC)中的人类白细胞抗原(HLA)基因座。平衡选择作用于HLA基因座,因为可变的HLA细胞表面抗原蛋白和其他免疫细胞配体(结合靶标)能提供更好的免疫功能。因此,HLA基因座是人类基因组中多态性最高的区域之一,每个基因座都表现出许多等位基因(Solberg等2008)。另一个著名案例——非洲疟疾区血型蛋白基因型与镰刀型细胞贫血——将在第7章详细讨论。
| |
|
| |
| <span id="如何解释同工酶多态性水平-1"></span>
| |
| ==== 如何解释同工酶多态性水平 ====
| |
|
| |
| 群体遗传学中另一场长期争论源自经典假说/平衡假说辩论。新争议围绕如何解释通过当时革命性新技术观察到的自然种群内遗传多态性。该技术是酶多态性的凝胶电泳分析,即同工酶(见<math display="inline">\operatorname{Box}2.2</math>)。1966年发表的两篇论文开启了这场新争议。Hubby和Lewontin(1966“)基于15a0只''Drosophila pseudoobscura''个体多个种群的21个基因座,提出了杂合度的同工酶估计值。其中9个基因座在种群内呈现2至6个等位基因的分离。Hubby和Lewontin的论文展示了一种可用于确定多等位基因基因座比例及各多态基因座杂合度水平的技术。
| |
|
| |
| 关于同工酶多态性成因的争议在1960年代中期开始的短短几年内改变了群体遗传学的研究重心。最初,经典假说和平衡假说被认为是主要解释。实际上,在与同工酶数据同时发表的论文中,Lewontin和Hubby(1966)提出:观察到的杂合度水平(种群平均30%的基因座呈多态性)与平衡假说不符,因为这需要承受相应的分离负荷(见第7章”遗传负荷”部分)。在当时背景下,对同工酶多态性的剩余解释是符合经典假说的定向自然选择。
| |
|
| |
| <span id="第6章-综述"></span>
| |
| = 第6章 综述 =
| |
|
| |
| 平衡假说在同期遭遇了来自实证数据的挫折。玉米中表现出的明显超显性被证明会随世代更替而衰减(Moll et al. 1964;综述见 Crow 1993b)。真正的超显性应仅作为杂合度的函数而无限持续。然而这些玉米实验结果符合以下预测:超显性实际上是由携带有利显性等位的基因座与携带有害隐性等位的其他基因座之间的配子不平衡所引起。当两个个体在两个此类基因座上分别纯合不同等位时,杂交后代的适应度会显著提升,因为隐性有害表型将被显性掩盖。玉米实验表明,表观超显性现象是由简单显性与连锁的共同作用导致,而非真实超显性。
| |
|
| |
| 经典假说/平衡假说的争论很快消退。选择中性(见第8章)作为经典假说框架下的解释,预测种群中遗传变异水平较低。这一关于选择中性等位的理念始于1950-1960年代的理论发展与数学形式化,并逐渐成为遗传多态性的主要零假设。中性理论假设许多基因座存在选择中性的等位,且多态性是新中性突变因遗传漂变所经历的非平衡随机游走的产物(Kimura 1983)。
| |
|
| |
| 平衡假说的式微与经典假说两大要素的崛起,共同形成了被Lewontin(1974)称为”群体遗传学新古典理论”的框架。这一标签的提出,是因为经典假说对多态性的解释中两个要素——选择中性突变与受定向或净化选择作用的突变——均源自早期经典假说。在新古典假说下,争论焦点转为中性突变与受自然定向选择作用的突变对遗传多态性水平的相对贡献。针对经典假说中自然选择要素的研究仍在持续,并通过更精细的理论模型与生态遗传学研究获得实证支持与理论更新。平衡假说至今仍具现实意义,实证证据表明平衡选择确实在自然种群中发挥作用(Charlesworth 2006;Fijarczyk and Babik 2015)。
| |
|
| |
| = 自然选择的群体遗传学 =
| |
|
| |
| 达尔文(''Darwin'')的自然选择概念与孟德尔(''Mendelian'')的颗粒遗传理论的综合构成了群体遗传学的基础,这一综合被称为'''新达尔文主义(neo-Darwinism)'''。<br />
| |
| - 对于单倍体生物,自然选择是一种种群增长过程,其中不同基因型因基因型特异性种群增长率不同而产生差异。基因型特异性增长率的比值称为'''相对适合度(relative fitness)''',它预测了在无限扩张的种群中随时间推移将趋向固定的基因型。<br />
| |
| - 当重组不存在时,自然选择可能导致'''克隆干扰(clonal interference)''',即有益单倍型相互竞争,只有最适合的单倍型达到固定,其他单倍型则丢失。<br />
| |
| - 二倍体生物的自然选择同样依赖相对适合度来体现基因型特异性增长率,但由于有性生殖的存在,父母配对后可通过随机交配在子代中产生可预测的基因型频率。
| |
|
| |
| * 自然选择对双等位基因位点存活率的影响可概括为:
| |
| ** '''定向选择(directional selection)'''(纯合子最适合),导致等位基因固定或丢失(或接近固定/丢失);<br />
| |
|
| |
| ** '''平衡选择(balancing selection)'''(杂合子优势),使两个等位基因永久共存;<br />
| |
|
| |
| ** '''分裂选择(disruptive selection)'''(杂合子劣势),根据初始基因型频率导致等位基因固定或丢失。
| |
| * '''自然选择基本定理(fundamental theorem of natural selection)'''表明,自然选择引起的平均适合度变化与适合度的加性遗传变异成正比。
| |
| * 存活表型的显性和隐性程度会影响自然选择下基因型频率的变化速率,因为基因型与表型间并非完美对应。当基因作用为加性时,自然选择对基因型频率的改变最快。
| |
| * '''经典假说(classical hypothesis)'''预测定向选择在自然种群中普遍存在,导致大多数位点的遗传多态性受限。现存遗传变异主要由有害突变解释,辅以少量中性突变和极少数有益突变。
| |
| * '''平衡假说(balance hypothesis)'''预测由于适合度超显性导致的平衡选择在自然种群中常见,并预测应有大量遗传多态性通过选择维持。该假说还推测选择会导致基因组较大区域出现配子不平衡。
| |
|
| |
| <span id="延伸阅读-1"></span>
| |
| = 延伸阅读 =
| |
|
| |
| 现代综合学派首次系统阐述自然选择且至今仍有阅读价值的著作:
| |
|
| |
| Fisher, R.A. (1999). ''The Genetical Theory of Natural Selection: A Complete Variorum Edition''. Oxford: Oxford University Press(初版于1930年).
| |
|
| |
| 另一部奠定孟德尔遗传学与自然选择数学联系的现代综合经典:
| |
|
| |
| Haldane, J.B.S. (1990). ''The Causes of Evolution''. Princeton, NJ: Princeton University Press(初版于1932年).
| |
|
| |
| 关于从达尔文、孟德尔到费舍尔、霍尔丹和赖特的早期群体遗传学史,参见:
| |
|
| |
| Provine, W.B. (1971). ''The Origins of Theoretical Population Genetics''. Chicago, IL: University of Chicago Press(此书初版于1971年,2001年版包含Provine的后记)。
| |
|
| |
| 关于群体遗传学中同工酶时代中期对经典假说/平衡假说辩论的广泛思考与批判,参见:
| |
|
| |
| Lewontin, R.C. (1974). ''The Genetic Basis of Evolutionary Change''. New York: Columbia University Press.
| |
|
| |
| = 章末练习题 =
| |
|
| |
| 1 假设一个群体包含两种单倍型,其绝对适合度值为<math display="inline">\hat{\ l}_{\mathfrak{A}}=\hat{\mathrm{~0.8~}}</math>和<math display="inline">\hat{\ l}_{\mathfrak{B}}=0.9</math>,初始群体大小为<math display="inline">N_{\mathrm{A}}=1000</math>和<math display="inline">N_{\mathrm{B}}=1000</math>。下一代的预期群体大小是多少?经过一代自然选择后,单倍型频率的预期值是多少?
| |
|
| |
| 2 一个群体最初由4000个''AA''、5100个''Aa''和3000个''aa''个体组成。经历严冬后,存活并繁殖的个体为3000个''AA''、3400个''Aa''和1500个''aa''。
| |
|
| |
| <ol style="list-style-type: upper-alpha;">
| |
| <li>计算每种基因型的绝对适合度、相对适合度和选择系数。<br />
| |
| </li>
| |
| <li>基于这些相对适合度值,预测再经历一代自然选择后的基因型频率和等位基因频率。将(A)中繁殖个体的基因型和等位基因频率作为初始频率,并假设随机交配。</li></ol>
| |
|
| |
| 3 一个群体的绝对适合度值为<math display="inline">W_{\mathrm{AA}}=0.7</math>、<math display="inline">W_{\mathrm{Aa}}=0.8</math>和<math display="inline">W_{\mathrm{aa}}=0.9</math>。另一个独立群体的绝对适合度值为<math display="inline">W_{\mathrm{AA}}=0.85558</math>、<math display="inline">W_{\mathrm{Aa}}=0.97779</math>和<math display="inline">W_{\mathrm{aa}}=1.1</math>。每个群体中各基因型的相对适合度值是多少?每个群体中哪些基因型(或等位基因)的频率会增加?在自然选择下,每个群体的平均适合度<math display="inline">(\overline{{\boldsymbol{\mathrm{w}}}})</math>将如何随时间变化?每个群体的总群体大小(''N'')将如何随时间变化?此例说明了绝对适合度与相对适合度的哪些区别?
| |
|
| |
| 4 当存在随机交配时,自然选择能否彻底清除群体中完全隐性的强有害等位基因?为什么能或不能?若存在近亲交配呢?
| |
|
| |
| 5 <math display="inline">\overline{{\boldsymbol{W}}}</math>与平衡状态下的基因型频率和等位基因频率有何关系?
| |
|
| |
| 6 若群体中普遍存在适合度的超显性,你预期遗传多态性水平会如何?相比之下,若定向选择普遍存在,预期的多态性水平又如何?使用正文中模拟网站的结果支持你的答案。
| |
|
| |
| 7 检索文献,寻找一篇近期利用本章涵盖的群体遗传学预测的研究论文。
| |
|
| |
| 研究主题可以是任何生物、应用或过程,但论文必须包含对方向选择、相对适合度、超显性或群体平均适合度等主题的假设检验。总结论文的主要假设、目标或理论基础。然后解释论文如何利用本章的群体遗传学预测,并总结基于该预测的结果和结论。
| |
|
| |
| 8 构建一个作用于双等位基因单一基因位点的自然选择模拟模型。构建电子表格模型的指导可在教材网站上找到。这些指导也可用编程语言如Python或R实现。
| |
|
| |
| = 问题框答案 =
| |
|
| |
| = 问题框6.1答案 =
| |
|
| |
| 通过初始和最终等位基因频率及经过时间求解相对适合度时,需对方程6.8取对数进行变形:
| |
|
| |
| 耐药等位基因的相对适合度是野生型等位基因的98%,因此当不存在AZT时,野生型等位基因频率会随时间增加。
| |
|
| |
| = 问题框6.2答案 =
| |
|
| |
| <math display="block">
| |
| \log\left(\frac{q_{t}}{p_{t}}\right)=t\log\left(w\right)+\log\left(\frac{q_{0}}{p_{0}}\right)
| |
| </math>
| |
|
| |
| <math display="block">
| |
| p_{equilibrium}=t/(s+t)=0.2/(0.1+0.2)=2/3
| |
| </math>
| |
|
| |
| 对于平衡等位基因频率:
| |
|
| |
| <math display="inline">\mathsf{P}></math>用于消除指数。令<math display="inline">p</math>表示野生型等位基因频率,<math display="inline">q</math>表示耐药等位基因总频率。基于等位基因频率估计间隔601天,世代数<math display="inline">t=231</math>。代入数值得:
| |
|
| |
| <math display="block">
| |
| \begin{array}{l}{{\overline{{w}}=0.9\big(0.667\big)^{2}+(1)2\big(0.667\big)\big(0.333\big)}}\ {{{}}}\ {{\qquad+0.8\big(0.333\big)^{2}=0.9333}}\ {{{}}}\ {{\hat{\mathfrak{h}}^{\prime}p=\frac{\big(0.667\big)\big(0.333\big)\big[0.667\big(0.9-1\big)+0.333\big(1-0.8\big)\big]}{0.9333}=0}}\end{array}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \log\left({\frac{0.51}{0.49}}\right)=(231)\log\left({w}\right)+\log\left({\frac{0.99}{0.01}}\right)
| |
| </math>
| |
|
| |
| <math display="block">
| |
| 0.01737=(231)\log(w)+1.9956
| |
| </math>
| |
|
| |
| <math display="block">
| |
| -1.9782=(231)\log{(w)}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| -1.9782/231=\log{(w)}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| 10^{-0.008564}=w
| |
| </math>
| |
|
| |
| 或通过边际适合度计算:
| |
|
| |
| <math display="block">
| |
| \begin{array}{r}{p_{t+1}=\frac{0.9\left(0.667\right)^{2}+1\left(0.667\right)\left(0.333\right)}{0.9333}=0.667}\ {\overset{\mathrm{\scriptsize~\uparrow~}^{n}}{\underset{\mathrm{\scriptsize~\uparrow~}^{n}}{}}p=0.667-0.667=0}\ {\overset{\mathrm{\scriptsize~At~}}{\underset{\mathrm{\scriptsize~\downarrow~}^{n}}{}}\left(p=0.9\left(p>p_{equilb\dot{n}\dot{n}\dot{m}}\right)\right.}\ {\left.\overline{{w}}=0.9\left(0.9\right)^{2}+\left(1\right)2\left(0.9\right)\left(0.1\right)+0.8\left(0.1\right)^{2}}\ {\phantom{\frac{\mathrm{\scriptsize~\uparrow~}^{n}}{\underset{\mathrm{\scriptsize~\downarrow~}^{n}}{}}}=0.917}\end{array}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \begin{array}{l}{{\displaystyle\hat{\mid}^{\prime\prime}p=\frac{(0.9)(0.)[0.9(0.9-1)+0.1(1-0.8)]}{0.917}}}\ {{\mathrm{}}}\ {{\mathrm{~=-0.0069}}}\end{array}
| |
| </math>
| |
|
| |
| 或通过边际适合度计算:
| |
|
| |
| <math display="block">
| |
| p_{t+1}={\frac{0.9(0.9)^{2}+1(0.9)(0.1)}{0.917}}=0.8931
| |
| </math>
| |
|
| |
| <math display="block">
| |
| {\hat{1}}^{\prime\prime}p=0.8931-0.9=-0.0069
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \mathsf{A t}p=0.2\left(p<p_{equilibrium}\right)
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \overline{{w}}=0.9(0.2)^{2}+(1)2(0.2)(0.8)+0.8(0.8)^{2}=0.868
| |
| </math>
| |
|
| |
| <math display="block">
| |
| {\hat{1}}^{\prime\prime}p={\frac{(0.2)(0.8)[0.2(0.9-1)+0.8(1-0.8)]}{0.868}}=0.0258
| |
| </math>
| |
|
| |
| 或通过边际适合度计算:
| |
|
| |
| <math display="block">
| |
| \begin{array}{c}{{p_{t+1}=\displaystyle\frac{0.9\bigl(0.2\bigr)^{2}+1\bigl(0.2\bigr)\bigl(0.8\bigr)}{0.868}=0.2258}}\ {{\hat{\mathrm{\Pi}}^{\prime\prime}p=0.2258-0.2=0.0258}}\end{array}
| |
| </math>
| |
|
| |
| 在 <math display="inline">p=0.9</math> 时,<math display="inline">\overline{W}</math> 低于平衡状态下的值。因此,<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math> 为负值,意味着自然选择导致等位基因频率下降。在 <math display="inline">p=0.2</math> 时,<math display="inline">\overline{W}</math> 仍低于平衡值。因此,自然选择引起的等位基因频率增加(正 <math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>)会导致平均适合度上升。在平衡点 <math display="inline">p_{\text{equilibrium}}</math> 处,<math display="inline">\overline{W}</math> 在这些相对适合度值下达到最大值;因此 <math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math> 为0,因为选择将不再改变等位基因频率。
| |
|
| |
| = 第7章 =
| |
|
| |
| === 自然选择的扩展模型 ===
| |
|
| |
| <span id="三等位或双位点的生存力选择模型"></span>
| |
| ==== 7.1 三等位或双位点的生存力选择模型 ====
| |
|
| |
| • 平均适合度曲面。<br />
| |
| aE单一位点上三等位的自然选择。<br />
| |
| aE双位点各两等位的自然选择。
| |
|
| |
| 第6章建立了一系列关于自然选择作用的一般性预测,前提是适合度等同于由单个双等位位点决定的基因型特异性生存力。基础双等位位点自然选择模型所需的条件具有较强限制性,在生物种群中可能不常满足。本章的目标是将自然选择模型的理解扩展到更复杂且更普适的遗传情景中。从这个意义上说,本章将探讨在更接近某些自然种群实际条件的假设下,自然选择的作用过程。第一节中,我们将保留生存力自然选择模型及其假设,但修改位点的等位数目和位点数量,目的是检验当适合度由单个三等位位点或双位点各两等位决定时,生存力选择的结果。
| |
|
| |
| 我们将使用一个称为'''适合度曲面'''的工具来理解自然选择下基因型频率、等位基因频率和平均适合度的动态变化。适合度曲面是一种图表,其轴线上显示种群的基因型频率,并在基因型频率范围内每个可能点上标注该种群的平均适合度。对于具有两或三个等位的单一位点,可使用 de Finetti 图作为适合度曲面,如图7.1所示。图中的三个轴代表种群基因型频率的分布。三角形内的每个点定义了三组基因型频率,随后用于计算种群的平均适合度。平均适合度通过颜色深浅及连接等适合度点的等高线表示。由于平均适合度的等高线图与用等高线表示海拔的地形图解释方式完全相同,因此它们也被称为'''适合度景观'''或'''适应景观'''。
| |
|
| |
| 适合度地形上的最高点代表了自然选择下的平衡基因型频率。适合度地形还展示了自然选择将如何随时间改变基因型频率——如果自然选择的作用方式像一名只能向上攀爬的徒步者。对于适合度地形上的任何一点,自然选择将提高种群的平均适合度,并将基因型频率向增加平均适合度的方向推移。一旦种群到达平均适合度无法再提升的位置,自然选择即达到平衡并停止改变基因型频率。在图7.1中,整个地形是一个倾斜平面;其最高点位于左侧顶点,即当''AA''基因型在种群中固定时的位置。因此,自然选择将改变基因型频率,使种群的平均适合度攀升直至''AA''基因型被固定。
| |
|
| |
| ==== 单一位点上三个等位基因的自然选择 ====
| |
|
| |
| 在理解适合度地形的基础上,我们现在转向人类血红蛋白<math display="inline">\hat{|}^{2}\mathrm{gene}</math>基因三个等位基因的经典自然选择案例(参见Allison 1956;Modiano等2001)。血红蛋白蛋白存在于红细胞中,负责结合氧气并将其从肺部运输至全身。成人血红蛋白由四个独立蛋白组成:两个<math display="inline">\hat{\mathsf{I}}\pm(\mathrm{or}\hat{\mathsf{a}}\notin\varphi\not\equiv\mathrm{a}\hat{\mathsf{a}}\not\in</math>蛋白和两个<math display="inline">\hat{|}2</math>(即α蛋白)。血红蛋白12基因编码<math display="inline">\hat{\mathsf{I}}^{2}</math>蛋白,通常被称为↑²珠蛋白或<math display="inline">Hb</math>。''Hb A''等位基因是人类种群中最常见的等位基因。尽管在人类种群中已发现数百种<math display="inline">Hb</math>等位基因,但''Hb S''等位基因是常见的低频等位基因。S等位基因的特征是核苷酸变化导致疏水性氨基酸缬氨酸取代了f2珠蛋白第六位氨基酸位置的亲水性谷氨酸。S等位基因纯合个体表现出红细胞形态学改变(镰刀化)和氧运输障碍,导致慢性贫血(Ashley-Koch等2000)。''Hb C''等位基因在西非和东南亚种群中也以低频存在。CC纯合个体通常表现为轻度至中度贫血和脾肿大,但常无症状(如Fairhurst和Casella 2004)。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/76f1290b37f89f29edbefb98b5c8cbfab5fc21e3dfaba970d2b6c297e7062f92.jpg]]
| |
|
| |
| 图 7.1 在双等位基因座三种基因型频率的德菲内蒂图中加入平均适合度形成的适合度曲面。彩色线条表示当自然选择提高种群平均适合度时,基因型频率的可能轨迹。适合度值为 <math display="inline">w_{\mathrm{AA}}=1.0</math>、<math display="inline">w_{\mathrm{Aa}}=0.6</math> 和 <math display="inline">w_{\mathrm{aa}}=0.2</math>,因此当种群固定为AA基因型时,最高平均适合度出现在左下顶点。从曲面上任意初始点持续增加平均适合度均可达到该最高适合度点。基因作用为加性,因为等位基因对基因型适合度的影响不随配对的等位基因改变而改变。A等位基因始终贡献0.5,a等位基因始终贡献0.1。
| |
|
| |
| 表7.1 西非疟疾流行地区血红蛋白i2基因六种基因型的相对适合度估计值。Cavalli-Sforza和Bodmer(1971)的数值基于与哈迪-温伯格预期基因型频率的偏离计算。Hedrick(2004)的数值通过AA、AC、AS和CC基因型个体的相对死亡率风险估计,并假设疟疾总体死亡率为20%。
| |
|
| |
| {|
| |
| !width="34%"|
| |
| !width="10%"| AA
| |
| !width="10%"| AS
| |
| !width="10%"| SS
| |
| !width="10%"| AC
| |
| !width="10%"| SC
| |
| !width="10%"| CC
| |
| |-
| |
| | '''Cavalli-Sforza和Bodmer(1971)的相对适合度(w)'''
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | Relativetowcc
| |
| | 0.679
| |
| | 0.763
| |
| | 0.153
| |
| | 0.679
| |
| | 0.534
| |
| | 1.0
| |
| |-
| |
| | RelativetoWAs
| |
| | 0.89
| |
| | 1.0
| |
| | 0.20
| |
| | 0.89
| |
| | 0.70
| |
| | 1.31
| |
| |-
| |
| | '''Hedrick(2004)的相对适合度(w)'''
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |-
| |
| | Relativetowcc
| |
| | 0.730
| |
| | 0.954
| |
| | 0.109
| |
| | 0.865
| |
| | 0.498
| |
| | 1.0
| |
| |-
| |
| | RelativetowAs
| |
| | 0.623
| |
| | 1.0
| |
| | 0.109
| |
| | 0.906
| |
| | 0.498
| |
| | 1.048
| |
| |}
| |
|
| |
| 血红蛋白基因型的适合度取决于人们生活的环境。在无疟原虫(''Plasmodium falciparum'')的地区,导致贫血及相关症状的基因型适合度较低。然而,在疟疾流行区域,某些''Hb''基因型能赋予对恶性疟原虫感染的抗性,这可能部分或完全抵消因贫血导致的适合度劣势。表7.1显示了西非疟疾流行地区六种''Hb''基因型相对适合度的两种估计值。
| |
|
| |
| 表7.1中一个看似明显的预测是:在疟疾流行的种群中,自然选择会增加CC基因型频率并最终固定C等位基因。但这种情况真的会发生吗?答案需要通过分析六种''Hb''基因型的适合度曲面来获得。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/a413c0905a1048a2a104a329f0178714d3690735f5cb31edb3169196cc440f8d.jpg]]
| |
|
| |
| 图7.2 当疟疾流行时,人类血红蛋白β基因A、S和C等位体的适合度曲面。图A中的曲面对应表7.1中顶部的适合度值组,而图B显示底部值组的曲面。由式7.3计算得出的圆形轨迹代表自然选择作用下等位基因频率随50个世代变化的路径。在图A中,当C等位体初始频率较高时,自然选择的平衡态是CC基因型的固定。相反,当C等位体初始频率较低(约小于7%)时,选择达到仅A和S等位体分离而C等位体丢失的平衡态。在图B中,无论C等位体初始频率如何,选择最终都会固定CC基因型。但当C等位体频率较低时,每世代C等位体的增量极小,因此选择需要数百个世代才能固定CC基因型。六个初始等位基因频率点(显示为空心圆)在两个曲面中是相同的。
| |
|
| |
| 对于三个等位体,存在六个基因型频率,这难以用图7.1中的de Finetti图表示。但由于等位基因频率之和必须为1,我们可以在三元图中表示适合度曲面,其中每个轴代表三个等位体之一的频率。图7.2展示了表7.1中两组适合度值对应的这类适合度曲面。与图7.1中的适合度曲面相比,这三个等位体的适合度曲面呈现出波动或丘陵状特征。
| |
|
| |
| 理解适合度曲面上基因型频率如何变化,需要计算曲面上各点的选择作用导致的等位基因频率变化。等位基因频率变化的符号和幅度将是我们所考察点上适合度曲面斜率的函数。为了对图7.2中的适合度曲面进行此类分析,我们需要将自然选择的生存力模型扩展至单一位点的三个等位体。我们可以计算种群的均适合度,其中<math display="inline">p,q</math>和<math display="inline">r</math>分别代表三个等位体A、B和C的频率。我们还可以使用包含各等位体的基因型的边际适合度,来计算某个等位体是否会因其携带基因型的平均适合度而增减频率。当随机交配时,A等位体的边际适合度为:
| |
|
| |
| <math display="block">
| |
| \begin{array}{r}{\overline{{w}}=w_{\mathrm{AA}}p^{2}+w_{\mathrm{BB}}q^{2}+w_{\mathrm{CC}}r^{2}+w_{\mathrm{AB}}2p q}\ {+w_{\mathrm{AC}}2p r+w_{\mathrm{BC}}2q r~}\end{array}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \overline{{w}}_{\mathrm{A}}=\frac{w_{\mathrm{AA}}p^{2}+w_{\mathrm{AB}}p q+w_{\mathrm{AC}}p r}{p}=w_{\mathrm{AA}}p+w_{\mathrm{AB}}q+w_{\mathrm{AC}}r
| |
| </math>
| |
|
| |
| 其中杂合基因型的频率乘以<math display="inline">\hat{\bf A}</math>%因为它们携带一个A等位体拷贝。边际适合度是一种比较当前世代<math display="inline">p</math>频率与自然选择改变基因型频率后下一世代<math display="inline">p</math>频率的方法。由于各等位体边际适合度与种群整体均适合度之间的差异,等位基因频率每世代都会发生变化。A等位体频率的变化量为:
| |
|
| |
| <math display="block">
| |
| \widehat{\sf I^{\prime}}p=p\frac{\left(\overline{{w}}_{\mathrm{A}}-\overline{{w}}\right)}{\overline{{w}}}
| |
| </math>
| |
|
| |
| 经过一代选择后的等位基因频率可简单表示为 <math display="inline">p_{t+1}=p+\hat{\mathsf{l}}^{\prime\prime}p</math>。B和C等位基因的表达式可通过类似方法轻松得出。此外需注意,只要基因型在每代选择作用前的初始状态符合Hardyaeinberg频率,该方法可扩展至单一位点上任意数量的等位基因。
| |
|
| |
| 回到适合度曲面,图7.2A是一个有趣的案例,因为它具有两个稳定平衡点。其中一个平衡点与表7.1的观察结果一致——CC基因型应通过选择达到固定。当C等位基因的初始频率较高时,使用式7.3计算的10代选择过程中所有三条等位基因频率轨迹都明显趋向CC固定。相反,当C等位基因初始频率较低时,频率轨迹显示C等位基因将从种群中消失。这一结果与CC基因型具有最高相对适合度的直觉相悖,其根源在于适合度曲面的特性:当C频率较低时,其边际适合度实际上低于平均适合度。换言之,适合度曲面在C等位基因频率升高的方向上呈下降趋势。由于自然选择仅作用于提高平均适合度,C等位基因频率因此持续降低直至消失。
| |
|
| |
| 为理解该适合度曲面可能引发的后果,假设人类种群中A和S等位基因比C等位基因更古老,且A和S已达到平衡频率。根据式6.35和表7.1,A等位基因的平衡频率为 <math display="inline">t/(s+t)=0.8/(0.11+0.8)=0.88</math>,因此S的平衡频率为 <math display="inline">1-0.88=0.11</math>。进一步假设C等位基因因突变在后期出现。由于突变率较低,C等位基因的初始频率必然较低,且大多数C等位基因将存在于AC和SC杂合子中。所有杂合子均表现超显性(AS)或亚显性(SC和AC)适合度。特别地,SC杂合子的相对适合度低于AA和AS基因型,因此在C频率较低时其边际适合度为负值。这意味着从C低频状态出发,必须经历平均适合度暂时下降的阶段才能实现C频率的初始增长。然而当C初始频率较高时,平均适合度将稳步上升直至CC固定。
| |
|
| |
| 因此,若A和S等位基因是祖先型,仅凭自然选择就足以导致新引入的C等位基因消失——尽管CC纯合子具有高相对适合度。
| |
|
| |
| <span id="问题框7.1-hb-c等位基因的边际适合度与hatmathsfiprimeprimep"></span>
| |
| = 问题框7.1 Hb C等位基因的边际适合度与<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math> =
| |
|
| |
| 使用表7.1顶部的相对适合度值,分别针对以下两组初始等位基因频率:<br />
| |
| 初始等位基因频率组1: <math display="inline">p=0.75</math>,<math display="inline">q=0.20</math>,<math display="inline">r=0.05</math><br />
| |
| 计算:<br />
| |
| 1. 平均适合度<br />
| |
| 2. C等位基因的边际适合度<br />
| |
| 3. 使用<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>的C等位基因频率变化
| |
|
| |
| 结合图7.2A预测两种初始频率下自然选择将达到的平衡状态。
| |
|
| |
| 初始等位基因频率设定2:<math display="inline">p=0.70</math>,<math display="inline">q=0.20</math>,<math display="inline">r=0.10</math>
| |
|
| |
| 对于图7.2B中的适合度曲面,自然选择最终会从C等位基因的任何初始频率固定CC基因型。然而当C等位基因频率较低时,选择对C等位基因频率的提升非常缓慢。这是因为在频率低于约15%且A等位基因频率较高时,C等位基因的边际适合度仅略微高于平均适合度。通过观察适合度曲面左侧顶点的等高线间距较大可以看出这一点。间距较大的等高线表示该区域坡度较小,即在一定基因型频率范围内种群平均适合度保持恒定或近似恒定。适合度曲面上的这些平坦区域可能是稳定或不稳定平衡点,也是选择作用较弱的区域,因为边际适合度值与平均适合度非常接近。
| |
|
| |
| 确定哪种不同的血红蛋白<math display="inline">\hat{\mathsf{I}}^{2}</math>基因型适合度值最能描述实际种群并非本示例的重点。相反,血红蛋白I²基因的例子说明:适合度的显性度、等位基因在种群中出现的顺序以及相对适合度值之间可能存在相互作用,共同决定三个等位基因情况下的自然选择结果。
| |
|
| |
| <span id="互动框7.1-单基因座上三个或更多等位基因的自然选择"></span>
| |
| = 互动框7.1 单基因座上三个或更多等位基因的自然选择 =
| |
|
| |
| 通过直接模拟单基因座上三个等位基因的选择过程,可以直观看出平衡点高度依赖于适合度的超显性和亚显性关系。Populus软件能够模拟含三个及以上等位基因位点的选择过程。启动Populus后,在Model菜单中选择Natural Selection,再选择Selection on a Multi-Allelic Locus。点击每个单选按钮查看不同的显示选项。注意使用默认适合度值时,<math display="inline">P_{3}</math>等位基因会趋于固定。通过拖拽右下角的标签可以放大选项对话框,更方便查看参数字段。
| |
|
| |
| 尝试修改以下适合度值:
| |
|
| |
| 加性<br />
| |
| <math display="inline">w_{32}=0.9</math>,<math display="inline">w_{33}=1.0</math><br />
| |
| 超显性:<math display="inline">w_{11}=W_{22}=W_{33}=0.3;</math><br />
| |
| 亚显性:<math display="inline">w_{11}=w_{22}=w_{33}=1.0;</math>
| |
|
| |
| 请确保为每组适合度值调整等位基因频率。可以尝试所有等位基因频率均设为<math display="inline">1/3</math>,或设置一个较常见的等位基因(默认值为0.67、0.12和0.21)。
| |
|
| |
| ==== 两个双等位基因座的自然选择 ====
| |
|
| |
| 由于表型(因而适合度)可能由多于一个基因座引起,将自然选择模型扩展到两个基因座是合乎逻辑的下一步。从生物学角度看,考虑多基因座选择有强烈动机,因为已知许多表型的变异由多个基因座引起(见第9章)。两个突变的命运也可被视为双基因座选择。由于配子不平衡的存在,双基因座的自然选择本质上比单基因座更复杂。如第2章所述,连锁和自然选择本身都会产生配子不平衡,这在双基因座自然选择模型中必须加以考虑。由于双基因座自然选择比单基因座复杂得多,本节的目的是对双基因座模型进行一般性介绍。重要的是要认识到,双基因座选择不像双等位基因座选择那样存在易于总结的平衡点集合。双基因座选择的结果取决于自然选择与基因座间重组的平衡,以及种群初始基因型频率。
| |
|
| |
| 双基因座自然选择通常从配子视角进行分析,因为配子不平衡以配子频率表示。对于两个双等位基因座,四种可能配子的结合会产生16种可能的基因型。设配子''AB''、''Ab''、''aB''和''ab''的频率分别为<math display="inline">x_{1}</math>、<math display="inline">x_{2}</math>、<math display="inline">x_{3}</math>和<math display="inline">x_{4}</math>。表7.2展示了四种配子所有可能组合的相对适合度值。若来自任一亲本的相同配子在子代基因型中具有相同的适合度,则仅有10个独特的适合度值。例如,若来自父本或母本的''Ab''配子在''AB''/''Ab''子代基因型中具有相同适合度,则适合度矩阵中<math display="inline">w_{12}=w_{21}</math>。
| |
|
| |
| 在随机交配和基因座间重组率为<math display="inline">c</math>的假设下,表7.3展示了10种可能亲本交配组合中各配子的期望频率(对比表2.12)。下一代各配子的频率可通过将表7.3中各列的期望频率加权求和获得,其中权重为各基因型的相对适合度。例如,经过一代自然选择和重组后''AB''配子的期望频率为:
| |
|
| |
| '''表7.2''' 两个双等位基因座形成的四种配子所有组合的适合度值矩阵(上)。若来自任一亲本的相同配子在子代基因型中具有相同适合度(如<math display="inline">w_{12}=w_{21}</math>),则存在10个位于阴影三角形外的配子适合度值。在双杂合子具有相等适合度(<math display="inline">w_{14}=w_{23}</math>)并以<math display="inline">W_{\mathsf{H}}</math>表示其适合度值的假设下,这10个适合度值可通过基因型适合度矩阵(下)概括。双杂合子基因型因能产生重组配子而具有特殊意义。
| |
|
| |
| <pre class="markdown"><table><tr><td></td><td>AB</td><td>Ab</td><td>aB</td><td>Ab</td></tr><tr><td>AB</td><td>W11</td><td>W12</td><td>W13</td><td>W14</td></tr><tr><td>Ab</td><td>W21</td><td>W22</td><td>W23</td><td>W24</td></tr><tr><td>aB</td><td>W31</td><td>W32</td><td>W33</td><td>W34</td></tr><tr><td>Ab</td><td>W41</td><td>W42</td><td>W43</td><td>W44</td></tr><tr><td></td><td>BB</td><td>Bb</td><td>Bb</td><td></td></tr><tr><td>AA</td><td>W11</td><td>W12</td><td>W22</td><td></td></tr><tr><td>Aa</td><td>W13</td><td>WH</td><td>W24</td><td></td></tr><tr><td>Aa</td><td>W33</td><td>W34</td><td>W44</td><td></td></tr></table>
| |
|
| |
| $$
| |
| \begin{array}{r l}{x_{1(t+1)}=}&{{}\underbrace{w_{11}x_{1}^{2}+w_{12}x_{1}x_{2}+w_{13}x_{1}x_{3}}_{\bar{W}}}\end{array}
| |
| $$
| |
|
| |
| 该式可直接与双等位基因单一位点的方程6.21相比较。通过展开$(1-c)w_{14}x_{1}x_{4}$项可简化为:
| |
|
| |
| $$
| |
| \begin{array}{c}{{x_{1(t+1)}=\displaystyle\frac{w_{11}x_{1}^{2}+w_{12}x_{1}x_{2}+w_{13}x_{1}x_{3}}{\bar{w}}}\end{array}
| |
| $$
| |
|
| |
| 接着将前四项提取$x_{1}$公因子,后两项提取$c$公因子:
| |
|
| |
| $$
| |
| x_{1(t+1)}=\begin{array}{c}{{x_{1}\big(w_{11}x_{1}+w_{12}x_{2}+w_{13}x_{3}+w_{14}x_{4}\big)}}\ {{-c\big(w_{14}x_{1}x_{4}-w_{23}x_{2}x_{3}\big)}}\ {{\bar{w}}}\end{array}
| |
| $$
| |
|
| |
| 若假设具有相同数目A和B等位基因的基因型适应度相等,则可进一步简化。例如,双重杂合体AB/ab和Ab/aB具有相同数目的A和B等位基因,因此可合理假设它们具有相同适应度值(表7.2)。该假设允许我们将那些因重组作用影响配子产生的双重杂合体的适应度值等同。将此假设应用于方程7.6时,可设$w_{14}~=~w_{23}$,则$c\left(w_{14}x_{1}x_{4}-w_{23}x_{2}x_{3}\right)$项可转化为$c w_{14}(x_{1}x_{4}-x_{2}x_{3})$,从而得到:
| |
|
| |
| **表7.3** 两个双等位基因位点在随机交配群体中生存力选择下的预期配子频率,位点间重组率为$c$。预期配子频率假设来自任一亲本的相同配子在子代基因型中具有相同适应度(例如$w_{12}=w_{21}$)。八种基因型产生的非重组和重组配子完全一致,因此无需重组率项。两种基因型会产生新型重组配子,需引入重组率来预测配子频率。对各列求和可得下一代因交配和重组产生的各配子总频率。</pre>
| |
| <pre class="markdown">| Genotype | Fitness | Total frequency | Frequency of gametes in next generation | | | |
| |
| |------------|---------|------------------|-----------------------------------------|-----|-----|-----|
| |
| | | | | AB | Ab | aB | ab |
| |
| | AB/AB | W₁₁ | | | | | |
| |
| | AB/Ab | W₁₂ | 2X₁X₂ | X₁X₂ | X₁X₂ | | |
| |
| | AB/aB | W₁₃ | 2X₁X₃ | X₁X₃ | | X₁X₃ | |
| |
| | AB/ab | W₁₄ | 2xX₄ | (1 - c)xₓ₄ | c xₓ₄ | c xₓ₄ | (1 - c)xₓ₄ |
| |
| | Ab/Ab | W₂₂ | X₂² | | | | |
| |
| | Ab/aB | W₂₃ | 2X₂X₃ | c X₂X₃ | (1 - c)X₂X₃ | (1 - c)X₂X₃ | c X₂X₃ |
| |
| | Ab/ab | W₂₄ | 2X₂X₄ | | X₂X₃ | X₂X₃ | |
| |
| | aB/aB | W₃₃ | X₃² | | | X₃² | |
| |
| | aB/ab | W₃₄ | 2X₃X₄ | | | X₃X₄ | X₃X₄ |
| |
| | ab/ab | W₄₄ | X₄² | | | | |
| |
|
| |
| $$
| |
| x_{1(t+1)}= \begin{array}{c}
| |
| {x_{1}\big(w_{11}x_{1}+w_{12}x_{2}+w_{13}x_{3}+w_{14}x_{4}\big)} \\
| |
| {-c w_{14}\big(x_{1}x_{4}-x_{2}x_{3}\big)}
| |
| \end{array}
| |
| $$
| |
|
| |
| 这有助于理解,因为配子失衡参数 $D$ 是耦合配子乘积与相斥配子乘积的差值(见公式2.27)。在本节符号中,$D=x_{1}x_{4}-x_{2}x_{3}$。因此我们可将公式7.7中的 $x_{1}x_{4}-x_{2}x_{3}$ 替换为 $D$,得到:
| |
|
| |
| $$
| |
| x_{1(t+1)}= \begin{array}{c}
| |
| {x_{1}\big(w_{11}x_{1}+w_{12}x_{2}+w_{13}x_{3}+w_{14}x_{4}\big)} \\
| |
| {-c w_{14}D}
| |
| \end{array}
| |
| $$
| |
|
| |
| 公式7.8表明,经过一代自然选择后AB配子的频率取决于三个因素。首先,产生AB配子的三种基因型(AB/AB、AB/Ab和AB/aB)的生存力会改变基因型频率,从而影响下一代AB配子的频率(重组不会改变这些基因型产生的AB配子频率)。其次,AB配子频率的额外部分由重组、双重杂合子的适合度值以及种群初始配子失衡共同决定。通过 $D$ 可测量双重杂合子的频率是否偏离随机交配预期值。此外,重组频率和基因型的相对适合度将决定产生多少AB配子。若忽略 $D$ 和 $r$,AB配子的频率将类似于单一位点四个等位基因中某一配子的频率。
| |
|
| |
| 本章前文针对单一位点推导的表达式可扩展至此。通过累加某配子可能配对形成基因型的所有配子的频率加权适合度值,可获得两位点配子的边际适合度 $\left(\overline{{\mathbf{w}}}_{i}\right)$:
| |
|
| |
| $$
| |
| \overline{{w}}_{i}=\sum_{j=1}^{4}x_{j}w_{i j}
| |
| $$
| |
|
| |
| 类似地,种群平均适合度是所有可能配子组合的频率加权适合度平均值:
| |
|
| |
| $$
| |
| \overline{{w}}=\sum_{i=1}^{4}\sum_{j=i}^{4}x_{i}x_{j}w_{i j}
| |
| $$</pre>
| |
| 边际适合度(marginal fitness)与平均适合度(mean fitness)可通过方程7.8结合,得到在选择和重组作用下配子频率变化的表达式。
| |
|
| |
| 以AB配子为例,注意边际适合度<math display="inline">\overline{{w}}_{1}</math>等于<math display="inline">x_{1}w_{11}+x_{2}w_{12}+x_{3}w_{13}+x_{4}w_{14}</math>。将此代入方程7.8,除以平均适合度,并用<math display="inline">W_{H}</math>替换<math display="inline">w_{14}</math>或<math display="inline">w_{23}</math>,可得自然选择作用下一世代内AB配子频率的变化:
| |
|
| |
| <math display="block">
| |
| \widehat{|}^{\prime\prime}x_{1}=\frac{x_{1}\overline{{w}}_{1}-c w_{H}D}{\overline{{w}}}
| |
| </math>
| |
|
| |
| 这与双等位基因位点的<math display="inline">\hat{\mathsf{I}}^{\prime\prime}p</math>表达式完全类似(对比方程6.23)。通过对其他三种配子进行类似推导,可得自然选择与重组作用下一世代后配子频率的递归方程组:
| |
|
| |
| <math display="block">
| |
| \begin{array}{l}{{\displaystyle{\hat{\left|}^{\prime\prime}{x_{2}}=\frac{x_{2}\overline{{{w}}}_{2}+c w_{H}D}{\overline{{{w}}}}\right.}}}\ {{\displaystyle{\hat{\left|}^{\prime\prime}{x_{3}}=\frac{x_{3}\overline{{{w}}}_{3}+c w_{H}D}{\overline{{{w}}}}\right.}}}\ {{\displaystyle{\hat{\left|}^{\prime\prime}{x_{4}}=\frac{x_{4}\overline{{{w}}}_{4}-c w_{H}D}{\overline{{{w}}}}\right.}}}\end{array}
| |
| </math>
| |
|
| |
| 基于”四种配子频率可视为单一位点上四个等位基因频率”的类比,我们可以利用部分…
| |
|
| |
| 方程7.11a-d表明,自然选择作用下的配子频率变化由适合度值和重组共同决定。若无重组(<math display="inline">\mathbf{\chi}_{c}=0</math>),则每个配子类似于单个等位基因。此时选择结果由配子适合度值决定,如同单一位点上的四个等位基因。重组过程可能增强或抵消自然选择引起的配子频率变化。例如:若配子Ab和aB具有最高适合度且无重组,则<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{2}</math>和<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{3}</math>为正,而<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{1}</math>和<math display="inline">\hat{\Gamma}^{\prime\prime}x_{4}</math>为负(非平衡状态时)。此时由重组引起的配子频率变化会放大自然选择效应,因为<math display="inline">c w_{H}D</math>项会增加<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{2}</math>和<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{3}</math>,同时减少<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{1}</math>和<math display="inline">\hat{\Gamma}^{\prime\prime}x_{4}</math>。相反,若配子AB和ab具有最高适合度且存在重组,则<math display="inline">c w_{H}D</math>项会减少<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{1}</math>和<math display="inline">\hat{\Gamma}^{\prime\prime}x_{4}</math>,但增加<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{2}</math>和<math display="inline">\hat{\mathsf{I}}^{\prime\prime}x_{3}</math>,从而与自然选择作用方向相反。
| |
|
| |
| 通过考察有重组和无重组情况下两个基因座的自然选择,可以发现选择与重组相互对抗能产生违反直觉的平衡配子频率。图7.3展示了一个基因作用完全加性的双基因座适合度曲面。由于适合度曲面是倾斜平面,我们先前在单基因座选择中的经验表明,自然选择的平衡点应是最高适合度位置。当重组相对于选择是弱势时(图7.3A),配子频率变化遵循适合度曲面的斜率,所有初始配子频率最终都会达到最高平均适合度的平衡点。然而当重组相对于选择是强势时(图7.3B),平衡配子频率则强烈依赖于初始配子频率。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/116416f578e469c53e80f98f57f3a58b91d3415bbcccd4aa39ab9a6afc24e345.jpg]]<br />
| |
| 图7.3 每个基因座具有两个等位基因的双基因座加性基因作用适合度曲面。蓝色点显示基于配子频率变化方程<math display="inline">(\hat{\vec{1}}^{\prime\prime}\vec{x}_{1}</math>至<math display="inline">\hat{\mathsf{I}}^{\prime\prime}{x_{4}}</math>)的逐代等位基因频率,对应七组不同的初始配子频率。当重组是弱势力<math display="inline">(c=0.05)</math>时,自然选择主导平衡等位基因频率,所有初始配子频率最终都会到达最高平均适合度点(A图)。相反,当重组是强势力<math display="inline">(c=0.5)</math>时,平衡等位基因频率取决于初始配子频率(B图)。强势重组下,平衡等位基因频率可能不对应最高平均适合度。相对适合度取值为<math display="inline">w_{\mathrm{AABB}}=0.9</math>,<math display="inline">w_{\mathrm{AABb}}=0.8</math>,<math display="inline">w_{\mathrm{AAbb}}=0.7</math>,<math display="inline">w_{\mathrm{AaBB}}=0.7</math>,<math display="inline">w_{\mathrm{AaBb}}=0.6</math>,<math display="inline">w_{\mathrm{Aabb}}=0.5</math>,<math display="inline">w_{\mathrm{aaBB}}=0.5</math>,<math display="inline">w_{\mathrm{aaBb}}=0.4</math>,<math display="inline">w_{\mathrm{aabb}}=0.3</math>。七个初始等位频率点(空心圆)在两个曲面中相同。
| |
|
| |
| 图7.4展示另一个双基因座选择的案例,其适合度曲面由于两个基因座的显性和上位效应形成鞍状双峰。当重组弱势时(图7.4A),平衡点取决于初始配子频率处适合度曲面的斜率,因为种群在强势选择作用下向高处移动。然而当重组相对于选择强势时(图7.4B),配子频率变化会与选择对抗,朝降低平均适合度的方向改变。如图7.3和7.4所示,强势重组下配子频率轨迹会发生急转,在重组力作用下沿适合度曲面下移。这是因为重组趋向配子平衡<math display="inline">(D=0)</math>,而选择趋向最高平均适合度。当某一过程显著强势时,它将主导平衡状态的确定。当两个过程强度相近时,结果会形成既不满足配子平衡也不达到最大平均适合度的折中平衡。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/23e10c5fe788f38b655965ad6507b03aab036adb8dd8ede484c06e2f13da66dc.jpg]]<br />
| |
| 图7.4 两个双等位基因位点的适合度曲面,展示上位效应的基因作用。当重组作用较弱时(<math display="inline">\mathit{\Pi}_{c}=0.05</math>),等位基因频率的平衡由自然选择决定。由于两个最高平均适合度点被适合度谷分隔,平衡等位基因频率取决于初始配子频率(图A)。当重组作用较强时(<math display="inline">\mathit{\Pi}_{c}^{\prime}=0.5</math>),等位基因频率的变化会导致平均适合度先下降一段时间后再次上升,最终达到两个平均适合度峰中较低的一个(图B)。曲面右上方的两个初始配子频率达到一个平衡点,此时适合度未达最大且存在配子不平衡(<math display="inline">\ensuremath{\left(D=0.041\right.}</math>)。相对适合度值为:<math display="inline">w_{\mathrm{AABB}}=0.61</math>,<math display="inline">w_{\mathrm{AABb}}=0.58</math>,<math display="inline">w_{\mathrm{AAbb}}=0.50</math>,<math display="inline">w_{\mathrm{AaBB}}=1.0</math>,<math display="inline">w_{\mathrm{AaBb}}=0.77</math>,<math display="inline">w_{\mathrm{Aabb}}=0.50</math>,<math display="inline">w_{\mathrm{aaBB}}=0.64</math>,<math display="inline">w_{\mathrm{aaBb}}=0.62</math>,<math display="inline">w_{\mathrm{aabb}}=0.92</math>。七个初始等位基因频率点(空心圆标示)在两个曲面中保持一致。
| |
|
| |
| 图7.4中的适合度曲面揭示了自然选择作用于两个位点的另一个重要特性。基因作用是决定自然选择最终达到平衡状态的关键变量。当两个位点呈现加性基因作用时,某个位点的基因型适合度不依赖于另一位点的基因型。这意味着基因型频率持续发生小幅变化(每次变化都提升平均适合度),最终将到达最高平均适合度。相反,在非加性基因作用(显性和上位效应)下,同样的等位基因频率逐代小幅变化可能导致局部最大值,因为适合度曲面不再是平面。当某个位点的基因型影响其他位点的适合度值时,平均适合度就会出现这样的峰谷结构。因此,随着显性和上位效应的增强以及加性基因作用的减弱,适合度曲面的地形复杂度会显著增加。基于此,自然选择有时被描述为短视或近视的,因为它基于每代的平均适合度运作,而非考虑整个适合度曲面的全局策略。其结果是,当平均适合度曲面存在多个极大值时,自然选择产生的平衡状态强烈依赖于初始基因型频率。
| |
|
| |
| 尽管对于具有任意一组适合度值的两座位选择,不存在通用的平衡配子频率集合,但已有许多特殊案例的研究得出了若干普遍结论(见Hastings 1981, 1986;Ewens 2004综述)。低重组频率(小c值)本身会增大选择在随机交配下仍导致平衡配子频率中出现配子不平衡的可能性。非加性基因作用与低频重组的结合也会增加平衡配子频率中配子不平衡的概率。高自交率(显著偏离随机交配)会对配子频率施加额外的作用力,这种作用力可能增强或抵消选择与重组的影响(Hastings 1985;Holsinger和Feldman 1985)。
| |
|
| |
| 由于平均适合度可能随选择和重组而降低,FisheraEfMndamental定理不适用于两座位选择(见Turner 1981;Hastings 1987)。研究两座位自然选择得出的一个关键结论是:除非在极限情况下(如重组极少且无上位效应),否则将单座位选择模型的结果推广到多座位可能在生物学上具有误导性。最后需注意,本文讨论的两座位模型特征是两个座位共同贡献于单一的适合度函数。因此,此处两座位模型与两个连锁座位各自具有独立适合度函数的模型(如Hillakobertson或Mullerae Ratchet模型)存在本质区别。
| |
|
| |
| <span id="自然选择的替代模型"></span>
| |
| ==== 7.2 自然选择的替代模型 ====
| |
|
| |
| •M 突破适合度作为无限增长种群中恒定生存力的假设。aEN通过不同生育力水平的自然选择 EN具有频率依赖性适合度的自然选择。
| |
|
| |
| E 具有密度依赖性适合度的自然选择
| |
|
| |
| 迄今考虑的自然选择模型将适合度等同于基因型的生存力。这相当于假设虽然不同基因型的个体在存活至成年阶段存在差异,但所有基因型在可能影响个体对下一代子代数量的其他表型特征上是相等的。再次观察图6.3,可见在生殖生命周期中存在多个基因型可能表现出差异成功或表现的节点。基因型可能在配子产生与存活、交配成功率、与其他配子的遗传相容性以及亲代抚育等表型特征上存在差异。甚至可能存在某些位点的等位基因在同源染色体分离过程中具有优势,从而更可能出现在配子中,这种现象称为''减数分裂驱动''(关于该过程的历史背景可参见Birchler等2003年的研究)。生命周期中的每个节点都是基因型可能表现出不同水平表现的场景,最终导致子代中基因型频率的差异。自然选择的基本生存力模型还假设适合度值在时间和空间上保持恒定。然而,适合度实际上可能因不同种群的环境条件或自然选择引起的基因型频率变化而发生改变。为了适应这些潜在的生物学情境,需要对自然选择模型进行修正。本节致力于通过多种方式扩展自然选择的基本生存力模型,以预测自然选择如何作用于适合度的不同组分及变化的适合度值。由于存在众多可能模型,无法详尽覆盖所有自然选择模型。相反,本节详述的三个模型将通过改变单一位点双等位基因生存力模型的主要假设之一,分别揭示自然选择动态的不同侧面。
| |
|
| |
| ==== 通过不同繁殖力水平的自然选择 ====
| |
|
| |
| 由于基因型生存力差异导致的自然选择有时被称为'''硬选择''',因为基因型频率的变化源于个体死亡及其完全丧失繁殖能力。相比之下,由于不同基因型个体的繁殖力(后代产量)差异引起的自然选择会导致每代子代中基因型频率的变化。繁殖力选择被称为'''软选择''',因为亲代中的所有个体均参与繁殖,尽管繁殖数量存在差异。
| |
|
| |
| 对双等位基因位点的自然选择建立繁殖力模型时,需要采取与生存力选择不同的方法。一个主要差异在于适合度取决于交配的基因型对。这意味着繁殖力选择模型中存在九种不同的适合度值,如表7.4所示。另一个差异是预测子代基因型频率将比简单随机交配的情况略微复杂。繁殖力的变异可能改变每对交配个体产生的子代数量,使其偏离单纯随机交配预期的频率。这需要考虑每对交配个体产生的预期子代基因型频率,并按该交配对的繁殖力进行加权,如表7.4所示。X、Y和Z分别表示基因型''AA''、''Aa''和''aa''的频率。这与第二章中证明哈迪-温伯格定律时使用的符号体系一致。
| |
|
| |
| 表7.4 基于双等位基因位点上雌雄基因型交配对繁殖力的适合度值,以及各可能交配对产生的子代基因型频率(按交配对繁殖力加权)。''AA''、''Aa''和''aa''基因型的频率分别用X、Y和Z表示。
| |
|
| |
| {|
| |
| ! 雄性基因型
| |
| ! 雌性基因型
| |
| !
| |
| !
| |
| !
| |
| |-
| |
| |
| |
| | ''AA''
| |
| | ''Aa''
| |
| | ''aa''
| |
| |
| |
| |-
| |
| | ''AA''
| |
| | f₁₁
| |
| | f₁₂
| |
| | f₁₃
| |
| |
| |
| |-
| |
| | ''Aa''
| |
| | f₂₁
| |
| | f₂₂
| |
| | f₂₃
| |
| |
| |
| |-
| |
| | ''aa''
| |
| | f₃₁
| |
| | f₃₂
| |
| | f₃₃
| |
| |
| |
| |}
| |
|
| |
| {|
| |
| ! 亲本交配组合
| |
| ! 繁殖力
| |
| ! 总频率
| |
| ! 子代基因型频率
| |
| |-
| |
| |
| |
| |
| |
| |
| |
| | ''AA''
| |
| |-
| |
| | ''AA'' × ''AA''
| |
| | f₁₁
| |
| | X²
| |
| | 1
| |
| |-
| |
| | ''AA'' × ''Aa''
| |
| | f₁₂
| |
| | XY
| |
| | 1/2
| |
| |-
| |
| | ''AA'' × ''aa''
| |
| | f₁₃
| |
| | XZ
| |
| | 0
| |
| |-
| |
| | ''Aa'' × ''AA''
| |
| | f₂₁
| |
| | YX
| |
| | 1/2
| |
| |-
| |
| | ''Aa'' × ''Aa''
| |
| | f₂₂
| |
| | Y²
| |
| | 1/4
| |
| |-
| |
| | ''Aa'' × ''aa''
| |
| | f₂₃
| |
| | YZ
| |
| | 0
| |
| |-
| |
| | ''aa'' × ''AA''
| |
| | f₃₁
| |
| | ZX
| |
| | 0
| |
| |-
| |
| | ''aa'' × ''Aa''
| |
| | f₃₂
| |
| | ZY
| |
| | 0
| |
| |-
| |
| | ''aa'' × ''aa''
| |
| | f₃₃
| |
| | Z²
| |
| | 0
| |
| |}
| |
|
| |
| 该繁殖力选择模型比生存力模型更复杂,因为用于求解一代后基因型频率的方程是亲代基因型频率的函数。通过将子代频率(表7.4中各列)按对应繁殖力加权求和,可获得繁殖力选择一代后各基因型子代的平均数量。对于''AA''基因型子代,其平均繁殖力<math display="inline">\bar{f}</math>为:
| |
|
| |
| <math display="block">
| |
| \bar{f}X_{t+1} = f_{11}X^{2} + f_{12}\frac{1}{2}XY + f_{21}\frac{1}{2}YX + f_{22}\frac{Y^{2}}{4}
| |
| </math>
| |
|
| |
| 化简得:
| |
|
| |
| X_{t+1}=f_{11}X^{2}+(f_{12}+f_{21})X Y+f_{22}Y^{2} $$
| |
|
| |
| 通过类似的步骤,_Aa_和_aa_基因型平均繁殖力的方程为:
| |
|
| |
| <math display="block">
| |
| \begin{array}{c}{{\displaystyle{\overline{{{f}}}Y_{t+1}=\left(\begin{array}{l}{{f_{12}+f_{21}}}\end{array}\right)\frac{1}{2}X Y+\left(\begin{array}{l}{{f_{13}+f_{31}}}\end{array}\right)X Z}}}\ {{\displaystyle{+\frac{1}{2}f_{22}Y^{2}+\left(\begin{array}{l}{{f_{23}+f_{32}}}\end{array}\right)\frac{1}{2}Y Z}}}\end{array}
| |
| </math>
| |
|
| |
| 以及
| |
|
| |
| <math display="block">
| |
| \overline{{{f}}}Z_{t+1}=f_{33}Z^{2}+\left(f_{32}+f_{23}\right)\frac{1}{2}Y Z+f_{22}\frac{1}{4}Y^{2}
| |
| </math>
| |
|
| |
| 总平均繁殖力<math display="inline">(\bar{f})</math>是各基因型平均繁殖力之和,因此<math display="inline">\overline{{f}}X_{t+1}</math>、<math display="inline">\overline{{f}}Y_{t+1}</math>和<math display="inline">\bar{f}Z_{t}+1</math>给出了繁殖过程后所有基因型后代占总后代数的比例。请将这些以基因型频率为函数的平均繁殖力方程与式6.21和6.22中以等位基因频率为形式的方程进行对比。由于繁殖力选择发生时随机交配的定义不再成立【“by definition”译为“依定义”】,我们无法为表7.4中所示的九种繁殖力值的任意组合找到一般平衡点。相反,必须通过考虑繁殖力值的特殊案例来理解繁殖力选择模型引起的基因型频率变化。
| |
|
| |
| 繁殖力选择的一个特例是,当交配的总繁殖力始终等于各基因型在每个性别的繁殖力值之和时,这种情况称为'''加性繁殖力'''(additive fecundities),类似于加性基因作用(Penrose 1949)。设雌性的繁殖力值为 <math display="inline">f_{\mathrm{AA}},f_{\mathrm{Aa}}</math> 和 <math display="inline">f_{\mathrm{aa}}</math>,雄性的繁殖力值为 <math display="inline">m_{\mathrm{AA}}</math>、<math display="inline">m_{\mathrm{Aa}}</math> 和 <math display="inline">m_{\mathrm{aa}}</math>。在加性繁殖力模型中,表7.4中给出的繁殖力值例如 <math display="inline">f_{11}=f_{\mathrm{AA}}+m_{\mathrm{AA}}</math> 和 <math display="inline">f_{12}=f_{\mathrm{AA}}+m_{\mathrm{Aa}}</math>。在加性繁殖力下,杂合子更高的繁殖力会导致两个等位基因在种群平衡状态下被维持,这与生存选择模型中的超显性现象类似。第二个特例是'''乘性繁殖力'''(Bodmer 1965)。例如,<math display="inline">f_{11}=f_{\mathrm{AA}}m_{\mathrm{AA}}</math> 和 <math display="inline">f_{12}=f_{\mathrm{AA}}m_{\mathrm{Aa}}</math>。根据三种基因型的繁殖力值,可能存在平衡点使得两个等位基因在种群中被维持。第三个被广泛研究的特例是当存在四个繁殖力参数,对应于每个交配对杂合度的水平(Hadeler 和 Liberman 1975;Feldman 等 1983)。在这些情况下,根据使用的具体繁殖力值,繁殖力选择也可能维持种群中的两个等位基因,因为当所有三种基因型频率非零时达到平衡点。然而,与基本的生存选择模型相比,繁殖力选择模型并不会更频繁地在任意适合度值下导致遗传变异的维持(Clark 和 Feldman 1986)。这意味着繁殖力模型预测自然选择在平衡时通常导致等位基因的固定或丢失,正如生存模型在定向选择中的表现。
| |
|
| |
| Pollak(1978)表明,平均繁殖力不一定会随着繁殖力选择而增加。这意味着与自然选择在双等位基因单基因座生存模型中最大化平均适合度的方式不同,繁殖力选择在平衡基因型频率下未必会最大化平均繁殖力。
| |
|
| |
| 转基因向日葵与野生向日葵之间的杂交为例,展示了如何利用简单的繁殖力选择模型理解等位基因频率的变化。通过转基因生物技术,将外源基因永久整合到农作物中已成为常规操作。这类转基因可能通过某些农作物与其野生近缘种(通常为杂草)之间的杂交逃逸到野外(Snow 和 Palma 1997 综述)。以向日葵为例,纯合农作物基因型与野生植株杂交产生的后代种子产量仅为野生植株的<math display="inline">2\%</math>,但其存活率与野生植株相同。Cummings 等(2002)建立了三个实验种群,其中半数个体为农作物-野生植物 F1 代杂种,半数个体为野生植株。在这些种群中,作物特异性等位基因的初始频率为<math display="inline">25\%</math>。三个同工酶位点上的作物特异性等位基因频率在下一代下降至约<math display="inline">5\%</math>。下一代的作物特异性等位基因频率与加性繁殖力模型的预测结果最为吻合。
| |
|
| |
| 频率依赖性选择被广泛用于解释自然选择如何维持遗传多态性,并在多种生物类群中积累了大量案例。Brisson(2018)综述了负频率依赖性选择可能难以与其他形式自然选择相区分的若干情境。
| |
|
| |
| 我们可以构建一个简单选择模型,其中适合度(作为基因型特异性存活力)取决于基因型频率,并因此随基因型频率变化而改变。频率依赖性选择模型的核心在于建立可变的适合度度量。假设某基因型的适合度随该基因型在种群中频率上升而下降,称为负频率依赖性。其相对适合度值为:
| |
|
| |
| ==== 自然选择与频率依赖性适合度 ====
| |
|
| |
| 在基础生存力模型中,我们将适合度值视为基因型的不变属性。另一种表述方式是:适合度值<math display="inline">w_{\mathrm{xx}}</math>不随环境条件或基因型频率变化而改变。直觉上,我们可能预期基因型的适合度会依赖于其在种群中的频率,而自然种群中确实存在频率依赖性适合度的直接证据。例如,果蝇(''Drosophila'')中具有不同染色体倒位基因型的雄性个体交配成功率取决于种群中染色体倒位的频率(见<math display="inline">\tilde{\mathsf{A}}</math>lvarez-Castro和Alvarez 2005)。在植物中,种群中不同花色的频率可能影响传粉者的访问频率,从而导致频率依赖性交配成功率(如Gigord等2001;Jones和Reithel 2001)。一个有趣的频率依赖性适合度案例来自坦噶尼喀湖慈鲷鱼(''Perissodus microlepis'')口部左右弯曲的形态——这些鱼类通过撕咬其他鱼类的鳞片为食。较稀有的表型似乎具有优势,推测是因为被攻击的鱼类会预判来自更常见口型方向的攻击(Hori 1993)。频率依赖性选择是平衡选择的一种形式(与杂合子优势共同存在),最早由E. B. Poulton于1884年描述(见Allen和Clarke 1984)。负
| |
|
| |
| <math display="block">
| |
| \begin{array}{r}{w_{\mathrm{AA}}=1-s_{\mathrm{AA}}p^{2}\\ {w_{\mathrm{Aa}}=1-s_{\mathrm{Aa}}2p q\\ {w_{\mathrm{aa}}=1-s_{\mathrm{aa}}q^{2}\end{array}
| |
| </math>
| |
|
| |
| 其中<math display="inline">s_{\mathrm{xx}}</math>表示基因型特异性选择系数。当基因型稀有时具有更高适合度,因为相对适合度会随着选择系数与基因型频率乘积的增加而降低。需注意选择系数本身是常数,可视为相对适合度的每单位频率下降量。
| |
|
| |
| 与其他选择模型类似,该自然选择模型的平衡点可通过确定等位基因频率变化量<math display="inline">(\Delta p)</math>等于0时的情况获得。生殖力选择下一代的等位基因频率变化表达式为:
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{p q s(q-p)(p^{2}-p q+q^{2})}{\overline{W}}}
| |
| </math>
| |
|
| |
| 该式对应所有基因型选择系数相等的特例(推导见数学框7.1)。当<math display="inline">p=1.0</math>和<math display="inline">p=0.0</math>时存在两个平衡点(固定与丢失),因为分子中的<math display="inline">pq</math>项为0。当<math display="inline">\boldsymbol{p}=1/2</math>时也存在平衡点,此时<math display="inline">q-p</math>项为0。
| |
|
| |
| 图7.5展示了当所有选择系数等于1时式7.19中的相对适合度值。值得注意的是,在<math display="inline">p=1/2</math>时,杂合子的适合度低于两种纯合子,因此该自然选择模型不
| |
|
| |
| <span id="数学框7.1-频率依赖性选择的等位基因频率变化"></span>
| |
| = 数学框7.1 频率依赖性选择的等位基因频率变化 =
| |
|
| |
| 从式6.23给出的生存力选择下等位基因频率变化表达式出发:
| |
|
| |
| $$
| |
|
| |
| ^{}p= $$
| |
|
| |
| 然后将方程7.19中给出的频率依赖性适合度值的定义代入。若所有基因型的选择系数相等(即均可用无下标的s表示),则可得
| |
|
| |
| <math display="block">
| |
| {\hat{\mathbf{l}}}^{\prime\prime}p={\frac{p q\left[p\left(1-s p^{2}-(1-s2p q)\right)+q\left(1-s2p q-\left(1-s q^{2}\right)\right)\right]}{\overline{{W}}}}
| |
| </math>
| |
|
| |
| 展开方括号内的项得到
| |
|
| |
| <math display="block">
| |
| \widehat{\sf1^{\prime}}p={\frac{p q\bigl[p-s p^{3}-p+s2p^{2}q+q-s2p q^{2}-q+s q^{3}\bigr]}{\overline{{\cal{W}}}}}
| |
| </math>
| |
|
| |
| 通过抵消正负<math display="inline">p</math>和<math display="inline">q</math>项并提取公因子<math display="inline">s</math>,可简化为
| |
|
| |
| <math display="block">
| |
| \hat{1}^{\prime\prime}p=\frac{p q s\big[-p^{3}+2p^{2}q-2p q^{2}+q^{3}\big]}{\overline{{w}}}
| |
| </math>
| |
|
| |
| 方括号内的项可进一步因式分解为
| |
|
| |
| <math display="block">
| |
| {\widehat{\sf I^{\prime\prime}}}p={\frac{p q s(q-p)\bigl(p^{2}-p q+q^{2}\bigr)}{\overline{{\cal W}}}}
| |
| </math>
| |
|
| |
| <span id="互动框7.2-频率依赖性自然选择"></span>
| |
| = 互动框7.2 频率依赖性自然选择 =
| |
|
| |
| Populus可用于模拟频率依赖性自然选择。在Model菜单中选择Natural Selection,然后选择Frequency-Dependent Selection (Diploid Model)。在模型对话框中,可为两个等位基因单一位点产生的三种基因型设置频率敏感的相对适合度值。s1、<math display="inline">S2.</math>和s3值分别对应方程7.19中的<math display="inline">S_{\mathsf{A A}},~S_{\mathsf{A a}},</math>和<math display="inline">S_{\mathsf{a a}}</math>。首先尝试输入s1=0.3_{}、s2=1.0_{}和s3=0.3。解释为何基因型特异性适合度随等位基因频率变化的图表(中间面板)呈现当前形态。
| |
|
| |
| 接着输入选择系数s1=0.7、s2=1.0_{}和s3=0.2。比较顶部面板中<math display="inline">p</math>随delta <math display="inline">p</math>变化的图表与底部面板中<math display="inline">p</math>随平均适合度变化的图表,观察平衡等位基因频率下的平均适合度。自然选择是否总是使等位基因频率达到与最大平均适合度对应的平衡?通过合理猜测,尝试找出使平衡等位基因频率与最大平均适合度值对应或不对应的选择系数组合。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/bd30483a83285de612c49a9b88ceec3fd425c71a8f39a34750c9ee84e343bad0.jpg]]<br />
| |
| 图7.5 频率依赖性自然选择下各基因型的相对适合度<math display="inline">({\boldsymbol{\mathrm{W_{XX}}}})</math>及等位基因A频率变化<math display="inline">(\hat{\mathsf{I}}^{\prime\prime}p)</math>。此案例中尽管杂合子适合度最低,但p=0.5处存在稳定平衡点。固定和丢失状态的两个不稳定平衡点以空心圆标出。此处相对适合度值为<math display="inline">w_{\mathrm{AA}}=\overline{{}}^{\star}1-s_{A A}p^{2}</math>、<math display="inline">w_{\mathrm{Aa}}=1-s_{A a}2p q</math>和<math display="inline">w_{\mathrm{aa}}=1-s_{a d}q^{2}</math>,其中SAA = SAa = Saa
| |
|
| |
| 为在自然选择模型中纳入此类限制,我们可修改基本的基因型特异性种群增长方程,使其既包含种群规模上限,也包含随种群规模变化的增长率。
| |
|
| |
| 一种具有上限的简单种群增长模型称为逻辑斯谛增长(logistic growth),其上限称为'''环境承载力'''(carrying capacity,符号为<math display="inline">K</math>)。逻辑斯谛增长通过以下公式描述了增长率与种群大小之间的反馈关系:
| |
|
| |
| <math display="block">
| |
| \hat{\mathsf{I}}_{\boldsymbol{\mathrm{s}}}=1+r-\frac{r}{K}N
| |
| </math>
| |
|
| |
| 其中<math display="inline">N</math>为种群大小,<math display="inline">r</math>为增长率(本章前文用<math display="inline">\lambda</math>表示增长率,可通过<math display="inline">\hat{\vert}_{\gg}=1+r</math>等价转化为<math display="inline">r</math>)。从生物学角度,<math display="inline">r</math>表示超过替换率1的额外增长率。当<math display="inline">N=0</math>时,<math display="inline">\frac{r}{K}N</math>为0,此时增长率达到最大值;但当<math display="inline">N=K</math>时,<math display="inline">\frac{r}{K}N</math>等于<math display="inline">r</math>,此时种群仅维持自身替换而大小不变。
| |
|
| |
| 通过定义基因型特异性的环境承载力(carrying capacities)和增长率,可将逻辑斯谛种群增长应用于双等位基因座(diallelic locus)的三种基因型,从而获得各基因型的绝对适合度值。维持平衡状态下的遗传变异需要适合度的超显性(overdominance)。然而,若各基因型具有独立的选择系数(independent selection coefficients),则通常不存在稳定的多态性。当三种基因型的适合度为任意值时,可能出现多种结果,其中许多情况下不存在稳定的多态性。
| |
|
| |
| ==== 密度依赖适合度下的自然选择 ====
| |
|
| |
| 大多数自然选择模型假设种群增长不受限制。本章第一节建立的模型(回顾式6.1)中,任一基因型未来一代的种群大小等于当前大小乘以一个常数。该模型显然不现实,因为所有生物的种群规模最终都会受到限制。生物个体受空间和资源限制,这些限制导致个体密度随时间变化时增长率发生改变。为此:
| |
|
| |
| <math display="block">
| |
| \begin{array}{r l}
| |
| &{\hat{\mathsf{I}}_{\mathrm{AA}}=1+r_{\mathrm{AA}}-\frac{r_{\mathrm{AA}}}{K_{\mathrm{AA}}}N}\\
| |
| &{}\\
| |
| &{\hat{\mathsf{I}}_{\mathrm{Aa}}=1+r_{\mathrm{Aa}}-\frac{r_{\mathrm{Aa}}}{K_{\mathrm{Aa}}}N}
| |
| \end{array}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \hat{\mathsf{I}}_{\mathrm{aa}}=1+r_{\mathrm{aa}}-\frac{r_{\mathrm{aa}}}{K_{\mathrm{aa}}}N
| |
| </math>
| |
|
| |
| 且
| |
|
| |
| 此处各基因型个体数之和等于种群总大小(<math display="inline">N_{\mathrm{AA}}+N_{\mathrm{Aa}}+N_{\mathrm{aa}}=N</math>)。种群的平均绝对适合度是各基因型<math display="inline">r</math>和<math display="inline">r/K</math>值的加权平均:
| |
|
| |
| <math display="block">
| |
| \hat{\sf I}_{\gg}=1+\bar{r}-\frac{\overline{{r}}}{K}N
| |
| </math>
| |
|
| |
| 其中<math display="inline">\bar{r}=p²r_{\mathrm{AA}}+2pqr_{\mathrm{Aa}}+q²r_{\mathrm{aa}}</math>,且<math display="inline">\frac{\bar{r}}{K}=p²\frac{r_{\mathrm{AA}}}{K_{\mathrm{AA}}}+2pq\frac{r_{\mathrm{Aa}}}{K_{\mathrm{Aa}}}+q²\frac{r_{\mathrm{aa}}}{K_{\mathrm{aa}}}</math>。
| |
|
| |
| 最后一步是利用上述结果修正先前无限制种群增长模型的结论,以纳入逻辑斯谛增长。首先,修正总种群大小的增长方程(无限制增长的式6.1)为:
| |
|
| |
| <math display="block">
| |
| N_{t+1}=\hat{\mathsf{I}}_{\gg}N_{t}
| |
| </math>
| |
|
| |
| 此方程预测总种群大小不会超过最大环境承载力。我们还可通过修正选择一代后的等位基因频率表达式来追踪等位基因频率随时间的变化:
| |
|
| |
| <math display="block">
| |
| p_{t+1}=\frac{\hat{\mathsf{I}}_{\mathrm{\mathcal{A}A}}p_{t}^{2}+\hat{\mathsf{I}}_{\mathrm{\mathcal{A}a}}p_{t}q_{t}}{\hat{\mathsf{I}}_{\mathrm{\mathcal{B}}}}
| |
| </math>
| |
|
| |
| 此为方程6.19的逻辑斯谛增长形式。
| |
|
| |
| 当AA基因型具有最高承载量时,图7.6展示了密度依赖自然选择作用下各基因型个体数与等位基因频率的变化。初始种群规模<math display="inline">N</math>极小时,所有基因型的个体数随时间增加。然而当<math display="inline">N</math>接近最低承载量时(本例中为<math display="inline">K_{\mathrm{aa}}</math>),aa个体的数量达到峰值后开始下降。这是因为aa的绝对适合度在最短世代数内趋近于1,而另外两个基因型因其承载量更高,仍持续增加个体数。同理,Aa基因型因具有次低承载量,其个体数随后也会经历相同现象。AA基因型具有最高承载量,其个体数最终增长至占据整个种群。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/1c3f3c550e6e3b1d14bc49c9ae641f0709e8327d33c327896c440348c5bb3103.jpg]]<br />
| |
| 图7.6 密度依赖自然选择对总规模为<math display="inline">N</math>的种群中不同基因型个体数(<math display="inline">N_{\mathrm{AA}}</math>、<math display="inline">N_{\mathrm{Aa}}</math>和<math display="inline">N_{\mathrm{aa}}</math>)及等位基因频率的影响。当<math display="inline">N</math>达到上限时,等位基因和基因型频率的平衡由具有最高承载量(K)的基因型决定。相比之下,当种群规模较小时,具有最高增长率(r)的基因型对等位基因频率影响最大。本示例中<math display="inline">K_{\mathrm{AA}}=10000</math>,<math display="inline">K_{\mathrm{Aa}}=9000</math>,<math display="inline">K_{\mathrm{aa}}=8000</math>,且<math display="inline">r_{\mathrm{AA}}=0.2</math>,<math display="inline">r_{\mathrm{Aa}}=0.25</math>,<math display="inline">r_{\mathrm{aa}}=0.3</math>。
| |
|
| |
| 密度依赖选择的普适性结论是:当种群接近其承载量时,三种基因型的承载量将决定最终的基因型与等位基因频率。当<math display="inline">K_{\mathrm{AA}}</math>最大时,A等位基因趋于固定;当<math display="inline">K_{\mathrm{aa}}</math>最大时,a等位基因趋于固定。若<math display="inline">K_{\mathrm{Aa}}</math>最大,则会出现两种等位基因共存的平衡状态;若<math display="inline">K_{\mathrm{Aa}}</math>最小,则A或a的固定取决于初始等位基因频率。这些结果与无限制增长模型具有定性的同构性。
| |
|
| |
| 相反,当种群数量被限制在较低水平时,密度依赖型和密度无关型自然选择的结果并不一致。在受高度干扰或不适宜生存的环境中,个体的繁殖输出较低或周转率较高,此时总种群大小<math display="inline">N</math>可能远低于环境容纳量。为理解这一现象,可参考基因型绝对适合度值的公式<math display="inline">7.27\hat{\mathsf{a}}\notin\{29</math>。当各基因型的<math display="inline">N</math>趋近于0时,<math display="inline">\textstyle{\frac{r}{K}}N</math>项也会趋近于0,导致各基因型的绝对适合度越来越由其特异性增长率决定。此时具有最高增长率的基因型应增长最快,并主导平衡状态下的基因型和等位基因频率(若<math display="inline">r_{\mathrm{AA}}</math>最高,则A固定;若<math display="inline">r_{\mathrm{aa}}</math>最高,则a固定;若<math display="inline">r_{\mathrm{Aa}}</math>最高,则两种等位基因均保留;若<math display="inline">r_{\mathrm{Aa}}</math>最低,则初始等位基因频率决定A或a的固定)。这种效应可见于图7.6,当种群较小时,等位基因频率朝着<math display="inline">p</math>频率降低的方向变化。尽管该种群在环境容纳量下预期会固定<math display="inline">p</math>,但aa基因型的增长率最大,因此在种群较小时对等位基因频率的影响最为显著。
| |
|
| |
| <span id="交互框7.3-密度依赖型自然选择"></span>
| |
| = 交互框7.3 密度依赖型自然选择 =
| |
|
| |
| Populus软件可用于模拟密度依赖型自然选择。在Model菜单中,选择Natural Selection,然后选择Density-Dependent Selection w/ Genetic Variation。在选项对话框中,可设置基因型特异性环境容纳量和增长率。点击Nine-Frequency单选按钮可显示九种初始等位基因频率的结果(Single Frequency按钮则以总种群大小<math display="inline">N_{.}</math>的形式显示结果)。<math display="inline">N</math>文本框设置初始种群大小。点击View按钮查看模拟结果。
| |
|
| |
| 模拟参数值:
| |
|
| |
| <math display="inline">K_{\mathrm{AA}}=8000</math>,<math display="inline">K_{\mathrm{Aa}}=8000</math>,和<math display="inline">K_{\mathsf{a a}}=10000;</math>;<math display="inline">r_{\mathsf{A A}}=0.4</math>,<math display="inline">r_{\mathrm{Aa}}=0.4_{.}</math>,和<math display="inline">r_{\tt a a}=0.3_{\cdot}</math>;世代数=100<br />
| |
| <math display="inline">K_{\mathrm{AA}}=8000</math>,<math display="inline">K_{\mathrm{Aa}}=10000_{\cdot}</math>,和<math display="inline">K_{\mathrm{aa}}=8000;</math>;<math display="inline">r_{\mathsf{A A}}=0.4</math>,<math display="inline">r_{\mathrm{Aa}}=0.3_{\cdot}</math>,和<math display="inline">r_{a a}=0.35_{\scriptscriptstyle*}</math>;世代数=100<br />
| |
| <math display="inline">K_{\mathrm{AA}}=8000</math>,<math display="inline">K_{\mathrm{Aa}}=6000</math>,和<math display="inline">K_{\mathrm{aa}}=9000;</math>;<math display="inline">r_{\mathsf{A A}}=0.5,</math> <math display="inline">r_{\mathrm{Aa}}=0.3_{\cdot}</math>,和<math display="inline">r_{\tt a a}=0.4</math>;世代数=100
| |
|
| |
| <span id="自然选择与其他过程的结合"></span>
| |
| ==== 7.3 自然选择与其他过程的结合 ====
| |
|
| |
| aE自然选择与遗传漂变的共同作用。<br />
| |
| aE中性基因流或自然选择下的遗传分化。<br />
| |
| aE自然选择与突变的平衡。
| |
|
| |
| af遗传负荷。
| |
|
| |
| 自然选择发生的同时,其他过程也在运行并对等位基因频率产生影响。这些其他过程可能与自然选择协同作用,共同趋向相同的平衡等位基因频率;或者它们可能对抗自然选择,导向不同的平衡等位基因频率。由于实际生物种群中可能同时存在多种群体遗传过程,因此将自然选择置于影响等位基因频率的其他过程背景中考虑非常重要。本节首先探讨自然选择与遗传漂变相互对抗时的等位基因频率,接着讨论自然选择与突变相互对抗的情况。当自然选择与其他过程协同作用时,这仅会缩短达到平衡所需的世代数,而不会改变平衡等位基因频率。
| |
|
| |
| ==== 自然选择与遗传漂变同时作用 ====
| |
|
| |
| Wright(1931)展示了当群体同时受到自然选择、遗传漂变和突变作用时,其具有特定等位基因频率的概率为:
| |
|
| |
| <math display="block">
| |
| \ddot{\sf1^{\dag}}(p)=C p^{(4N_{e}\hat{\sf1}\dot{\bf\slash4}1)}q^{(4N_{e}\hat{\sf1}\dot{\bf\slash2}1)}e^{(4N_{e}s p q)}
| |
| </math>
| |
|
| |
| 其中<math display="inline">\ddot{|\dag}</math>(发音为<math display="inline">{\hat{\mathsf{a}}}{\hat{\mathsf{a}}}{\hat{\mathsf{o}}}{\hat{\mathsf{a}}}{\hat{\mathsf{z}}</math>)表示概率密度,<math display="inline">p</math>和<math display="inline">q</math>为等位基因频率,<math display="inline">N_{e}</math>为有效种群大小,μ和ν为正向与反向突变率,<math display="inline">s</math>为选择系数,<math display="inline">C</math>为用于调整所有等位基因频率总概率之和为1.0的常数(针对每个<math display="inline">N_{e}s</math>值)。此方程是第三章讨论的遗传漂变集合种群的概率密度函数【“ensemble population”译为”集合种群”】。它描述了在给定有效种群大小和选择系数条件下,众多复制群体中任一群体在平衡时达到0到1之间任意等位基因频率的概率。
| |
|
| |
| 通过以图形形式考察其预测结果(图7.7),可以最直观地理解这个方程。当<math display="inline">N_{e}s</math>接近0时,可能是由于种群极小导致遗传漂变非常强烈,或者选择系数极小使得种群在仅存在漂变的情况下以中性方式演化。在这两种情况下,遗传漂变都是主导过程,最终将导致所有种群中的等位基因固定或丢失。图7.7中最低的<math display="inline">N_{e}s</math>值对应的种群,其等位基因频率最可能接近0或1,这与仅存在遗传漂变时的预期一致。
| |
|
| |
| 相反,<math display="inline">N_{e}s</math>在两种普遍情况下会取较大值:第一种是当有效种群规模非常大使得遗传漂变非常微弱,且存在有利于杂合子的自然选择时(s可以取较宽范围,只要不是极小值);第二种是当选择系数很大且有效种群规模至少有10个左右个体时(此时遗传漂变不极端)。图7.7中最大的<math display="inline">N_{e}s</math>值对应的种群,其等位基因频率最可能接近0.5。方程6.35显示,当<math display="inline">w_{AA}=w_{aa}</math>且种群无限大时,0.5是平衡选择下预期的平衡等位基因频率。因此,当<math display="inline">N_{e}s</math>很大时,选择强于漂变,平衡等位基因频率主要由自然选择决定。当<math display="inline">N_{e}s</math>处于中间值时,许多种群的平衡等位基因频率会介于仅存在遗传漂变或仅存在自然选择时预期的平衡频率之间。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/ba71e7c3802739b417ef0f86e0a6ebca4e4fd2e2653fe7e8b818d603c11c913a.jpg]]<br />
| |
| Figure 7.7 在适合度超显性选择(<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{aa}}=1</math>且<math display="inline">w_{\mathrm{Aa}}=1</math>)下,大量重复有限种群的等位基因频率预期分布。在无限种群中,平衡时的预期等位基因频率为0.5。但在有限种群中,平衡等位基因频率取决于自然选择与遗传漂变的平衡关系。这种平衡由有效种群规模与选择系数的乘积(<math display="inline">N_{e}S</math>)决定。低<math display="inline">N_{e}s</math>值意味着选择相对于漂变非常微弱,每个种群会达到固定或丢失状态。高<math display="inline">N_{e}s</math>值意味着选择相对于漂变占优,大多数种群的等位基因频率平衡在0.5附近。此处正反向突变率相等(均为0.00001)。
| |
|
| |
| 要总结自然选择与遗传漂变的平衡,Motoo Kimura 提出了一个适用于二倍体位点的简易经验法则(Kimura 1983)。若有效种群大小与选择系数的四倍乘积远小于1(<math display="inline">4N_{e}s<<1</math>),则选择相对于取样效应较弱,等位基因频率将由遗传漂变主导。反之,若该乘积远大于1(<math display="inline">4N_{e}s>>1</math>),则选择相对于取样效应较强,等位基因频率将由自然选择主导。当四倍有效种群大小与选择系数的乘积约等于1(<math display="inline">4N_{e}s\hat{\mathsf{a}}\%</math>)时,漂变与选择对等位基因频率的影响大致相当。
| |
|
| |
| 图7.8展示了黑腹果蝇(''Drosophila melanogaster'')实验室重复种群中遗传漂变与自然选择平衡的实例(Wright和Kerr 1954)。该图显示了108个重复种群在Bar位点的等位基因频率变化。每个种群每代由四雄四雌建立(由于Bar等位基因在雄性中呈半合子状态,有效种群大小相当于六而非八个二倍体个体)。尽管绝大多数种群因强烈自然选择偏向隐性表型的野生型纯合子而固定了野生型等位基因,但仍有三个种群在实验结束时固定了Bar等位基因。针对Bar纯合子的选择系数估计为0.63,由此得出实验中<math display="inline">4N_{e}s</math>的上限估计值为<math display="inline">\mathrm{\Delta}N_{e}</math>(实际值可能小于六)。即使在此<math display="inline">4N_{e}s</math>值下,自然选择仍不足以在所有种群中主导等位基因频率的平衡。
| |
|
| |
| 通过类比第4章讨论的遗传漂变与基因流平衡的关键量<math display="inline">N_{e}m</math>,我们也能从生物学角度理解<math display="inline">N_{e}s</math>。<math display="inline">N_{e}s</math>与<math display="inline">N_{e}m</math>均反映了两种力量的净平衡:一方面遗传漂变推动等位基因走向固定或丢失,另一方面自然选择或基因流作为反向驱动力促使等位频率趋向特定值。自然选择情形中,特定等位频率由基因型的相对适合度决定;而基因流情形中,特定等位频率则是所有繁殖群的平均等位频率。
| |
|
| |
| ==== 自然选择导致的种群间遗传分化 ====
| |
|
| |
| 自然选择常与遗传漂变、基因流等中性过程同时作用,对位点的遗传分化产生潜在相悖的影响。当相对适合度与亚种群或地理区域相关时,选择将塑造位点的种群分化。自然选择主要通过两种方式影响种群分化:当相对适合度值在种群间存在差异时,定向选择(即局域适应)将…
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/ea494e96e40ebc7da943d26bfe7dd816b143fcaf233882ebc6646ae6479ed434.jpg]]<br />
| |
| 图7.8 黑腹果蝇(''Drosophila melanogaster'')108个重复种群中Bar等位基因在10代中的频率变化(Wright和Kerr 1954)。每个种群初始由4雄4雌建立。Bar基因座位于X染色体,因此在雄性中呈半合子状态,使得有效种群大小相当于约六个个体。野生型等位基因纯合的黑腹果蝇个体眼睛呈椭圆形,而部分显性''Bar''等位基因的杂合子与纯合子则具有条形眼且小眼面数量减少。Bar等位基因纯合雌性子代产量仅为野生型等位基因纯合或杂合雌性的37%。尽管存在如此强烈的自然选择对抗''Bar'',仍有三个种群在实验结束时固定了该等位基因。可与图3.11中基因座为中性选择时的类似案例进行对比。
| |
|
| |
| <span id="互动框7.4-双等位基因座的自然选择与遗传漂变的平衡"></span>
| |
| = 互动框7.4 双等位基因座的自然选择与遗传漂变的平衡 =
| |
|
| |
| 您可使用文本模拟网站来模拟多个相同有限种群中遗传漂变与自然选择的联合作用。通过模拟菜单选择”漂变-选择-突变”模型。在对话框中勾选自然选择选项,并确保不勾选突变选项。
| |
|
| |
| 使用默认参数运行模型数次以理解输出结果。左侧图表显示多个复制基因座/种群随时间的等位基因频率轨迹。右侧直方图展示所有种群的等位基因频率分布(类似于图7.7中单个<math display="inline">N_eS</math>值的二维切片)。需注意:只要正反向突变率相等且非常微小(可通过设置0.1等高突变率观察影响),突变对等位基因频率结果几乎无作用。
| |
|
| |
| 模拟漂变与选择时,保持选择系数恒定而改变<math display="inline">N_e</math>。每次运行前应计算<math display="inline">4N_es</math>值,并预测种群间的等位基因频率分布。设定<math display="inline">W_{AA}=W_{aa}=0.9</math>且<math display="inline">w_{Aa}=1.0</math>(即<math display="inline">s=0.1</math>),分别对<math display="inline">N_e=5</math>、20和200进行模拟。
| |
|
| |
| 请描述直方图中各<math display="inline">N_es</math>水平对应的等位基因频率总体分布,并解释该图如何反映漂变与选择的相对平衡关系。
| |
|
| |
| 预期这将导致不同种群间基因型频率的差异,从而产生种群分化。反之,当各种群间适合度值一致时,方向性选择或平衡选择将维持多个种群间相似的基因型频率,以对抗遗传漂变,减少遗传分化。在所有这些情况下,选择系数需足够大使自然选择强度足以克服:1)遗传漂变导致的种群间等位基因频率随机化;2)基因流引起的等位基因频率均质化作用。
| |
|
| |
| 一种识别经历过自然选择的位点的方法是:对多个位点的样本进行逐个位点的模式观察,并根据中性演化模型和自然选择影响的预测,识别出具有异常值的位点。这一方法背后的基本原理源自Lewontin和Krakauer(1973)的一篇论文。他们指出,自然选择对每个位点的作用因基因型的相对适合度值和选择强度而异,而遗传漂变和基因流等中性过程对所有位点的作用具有随机变异的均匀性。其逻辑是:大多数位点处于中性或近中性演化状态,而受强自然选择作用的少数位点因其偏离中性位点的观测值范围而可被识别。
| |
|
| |
| Lewontin和Krakauer(1973)提出在基因流的岛屿模型假设下,利用样本位点的<math display="inline">\hat{F}_{ST}</math>演化方差来识别异常位点。他们对自然选择的预测包含两方面:首先,经历亚种群间相似选择压力的位点,其方差会小于仅因漂变分化的中性位点,因为选择会抵消等位基因频率的随机分化;其次,由于局域适应导致亚种群间选择系数异质的位点,其分化程度会强于仅因漂变分化的中性位点。但Lewontin和Krakauer(1973)检验的若干方面很快被指出是该方法的缺陷(Nei和Maruyama 1975;Robertson 1975a, 1975b;Nei和Chakravarti 1977;Nei等1977)。潜在问题包括:第一,若某些亚种群间的基因流速率高于其他组合(与岛屿模型相悖),则某些繁殖群的等位基因频率将存在相关性(非独立性),这可能违反<math display="inline">\hat{F}_{ST}</math>的方差假设(某些繁殖群间<math display="inline">\hat{F}_{ST}</math>的正协方差会增加<math display="inline">\hat{F}_{ST}</math>的总方差);第二,亚种群间的亲缘关系模式可能从均匀相关到层级相关,这种由突变随机时间导致的差异可能影响<math display="inline">\hat{F}_{ST}</math>的方差;第三,当时基因数据获取困难,导致<math display="inline">\hat{F}_{ST}</math>方差的精确估计存在实证难度;第四,由于<math display="inline">\hat{F}_{ST}</math>分布的随机计算机模拟难以实施,相关预期依赖于解析近似。
| |
|
| |
| 随着在基因组尺度上观察SNP遗传多态性方法的不断创新,现在可以通过极大样本量的位点来估计<math display="inline">\hat{F}_{ST}</math>的方差。(此类研究采用了模糊的术语“afoeome scans”)这促使人们重新致力于利用<math display="inline">\hat{F}_{ST}</math>的分布来识别经历自然选择的位点,并进一步开发适用于中性位点的零假设期望。例如,Akey等人(2002)使用来自三个群体(非裔美国人、东亚人和欧裔美国人)样本中约26 000个人类基因组单核苷酸多态性(SNP),并假设基因流的岛屿模型。Akey发现编码位点的SNP平均<math display="inline">\hat{F}_{ST}=0.107</math>,而编码区域的平均<math display="inline">\hat{F}_{ST}=0.123</math>,这与所有群体中普遍存在的净化选择一致。最终,174个位点被识别为<math display="inline">\hat{F}_{ST}</math>分布的离群值,因此被认为经历了强烈的自然选择。
| |
|
| |
| 关于中性位点间<math display="inline">\hat{F}_{ST}</math>值分布对亚群体间基因流模式、群体规模历史及增长率变化的敏感程度存在不同观点。在分划群体的溯祖理论中(见第4章),将时间尺度划分为浅层与深层时间的分离表明,由于谱系深层时间部分对多态性模式的影响强于近期浅层时间(迁移事件主要发生时期),<math display="inline">F_{ST}</math>分布可能对群体人口历史变异和基因流模式具有鲁棒性(见Beaumont 2005)。贝叶斯统计估计方法(Foll和Gaggiotti 2008)解决了一系列可能导致假阳性鉴定离群位点的潜在缺陷,该方法通过计算每个位点自然选择模型与中性遗传分化模型的后验概率来实现。
| |
|
| |
| 相反,模拟研究表明<math display="inline">\hat{F}_{ST}</math>分布会因不同基因流模型而存在差异,这使得离群位点的推断依赖于用于建立零分布的基因流模型。Excoffier等人(2009a)在无限等位基因模型和逐步突变模型下对遗传位点进行计算机模拟,比较了岛屿模型和分层岛屿模型的<math display="inline">\hat{F}_{ST}</math>分布。他们证明:当群体实际经历分层岛屿模型的基因流模式时,使用有限岛屿模型对<math display="inline">\hat{F}_{ST}</math>分布的预期会导致大量假阳性离群位点。此外,他们重新分析了人类和''stickleback fish''的SNP实证数据集,显示分层岛屿模型预期下的离群位点数量远少于岛屿模型。图7.9通过经典岛屿模型与分层岛屿模型模拟的<math display="inline">\hat{F}_{ST}</math>分布展示了该模式。虽然两种分布的平均<math display="inline">\hat{F}_{ST}</math>几乎相同,但分布形状存在差异,尤其是分布尾部位点比例不同。中性位点间重组率的变化也可能影响<math display="inline">\hat{F}_{ST}</math>分布的形状(Booker等人 2020)。
| |
|
| |
| 对<math display="inline">\hat{F}_{ST}</math>离群值方法的实证验证研究也通过检测已知经历强自然选择的基因座的<math display="inline">\hat{F}_{ST}</math>来开展,常使用人类遗传数据。例如,Lohmueller等(2006)检测了欧洲和非洲人群间48个已知与疾病表型相关基因座的SNP位点的<math display="inline">\hat{F}_{ST}</math>,但发现这些基因座并未呈现离群<math display="inline">\hat{F}_{ST}</math>值(参见Myles等2008、Adeyemo和Rotimi 2010的类似研究)。相反,Brandt等(2018)发现主要组织相容性复合体(MHC)中的人类白细胞抗原(HLA)基因比其他基因座具有更低的<math display="inline">\hat{F}_{ST}</math>,这与因适合度超显性导致的平衡自然选择一致(另见Marigorta等2011)。
| |
|
| |
| 尽管用于估计更多样化物种中大量基因座<math display="inline">\hat{F}_{ST}</math>的经验基因组数据正变得越来越普遍,但Lewontin-Krakauer检验的根本挑战依然存在。检测基因座是否表现出偏离中性零模型预期遗传分化的测试,将需要仔细考虑<math display="inline">\hat{F}_{ST}</math>分布的零模型中众多方面,包括多种可能的基因流模型。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/5deb8e2993095d25c6b9669e41def71e58165acec7b0b8320689fe1e60991fa4.jpg]]<br />
| |
| 图7.9 基因流岛屿模型和层级岛屿模型下,110代后1000个独立双等位基因座的<math display="inline">\hat{F}_{ST}</math>分布。两种分布的中心趋势近乎一致(<math display="inline">F_{ST}</math>(岛屿模型)=0.2626,<math display="inline">F_{ST}</math>(层级模型)=0.2548),但分布形态和尾部存在差异。<math display="inline">\hat{F}_{ST}</math>分布的差异会影响对基因座是否偏离中性演化零模型预期分化的判断。模拟参数为:20个亚群体,每个<math display="inline">N_e=20</math>;岛屿模型迁移率<math display="inline">m=0.04</math>;层级模型中组内deme间迁移率<math display="inline">m_d=0.05</math>,组间迁移率<math display="inline">m_g=0.02</math>(4个组,每组5个deme),无突变。
| |
|
| |
| ==== 自然选择与突变的平衡 ====
| |
|
| |
| 自然选择发生的同时,突变也在改变等位基因频率并重新引入可能被选择淘汰的等位基因。因此,自然选择过程可能在一定程度上被突变抵消。如果一个完全隐性等位基因在纯合时既具有有害性又通过自发突变产生,其频率将受到相反方向的作用力影响。突变压力将持续将该等位基因重新引入群体,而自然选择将持续推动其走向丢失。当突变与自然选择这两个相反过程达到平衡时,预期的平衡等位基因频率是多少?
| |
|
| |
| 假设在一个位点上有两个等位基因,且''a''等位基因完全隐性,其频率为<math display="inline">q</math>。同时,假设如'''表6.4'''所示的选择对抗隐性等位基因的情况。通过将适合度值<math display="inline">w_{\mathrm{AA}}=w_{\mathrm{Aa}}=1</math>和<math display="inline">\mathrm{{w_{aa}=1-s}}</math>代入式6.24,可以得到自然选择对抗隐性纯合子这一特定情况下等位基因频率每代变化的表达式:
| |
|
| |
| <math display="block">
| |
| \hat{\mathbf{\widetilde{\Gamma}}}^{\prime\prime}q_{selection}=\frac{p q[q((1-s)-1)+p(1-1)]}{(1)p^{2}+(1)2p q+(1-s)q^{2}}
| |
| </math>
| |
|
| |
| 经整理后简化为:
| |
|
| |
| <math display="block">
| |
| \hat{\mathsf{I}}^{\prime\prime}q_{selection}=\frac{-s p q^{2}}{1-s q^{2}}
| |
| </math>
| |
|
| |
| 进一步假设突变是不可逆的,且''A''等位基因突变为''a''等位基因的概率为<math display="inline">\mu</math>。则每代由突变引起的等位基因频率变化为:
| |
|
| |
| <math display="block">
| |
| \hat{\mathsf{I}}^{\prime\prime}q_{mutation}=\mu p
| |
| </math>
| |
|
| |
| 在平衡状态下,自然选择推动等位基因固定化的作用与突变增加等位基因频率的压力达到精确平衡,此时等位基因频率不再变化。这意味着在平衡时:
| |
|
| |
| <math display="block">
| |
| \hat{\mathsf{I}}^{\prime\prime}q_{mutation}+\hat{\mathsf{I}}^{\prime\prime}q_{selection}=0
| |
| </math>
| |
|
| |
| 将<math display="inline">\hat{\mathsf{I}}^{\prime\prime}q_{mutation}</math>和<math display="inline">\hat{\mathsf{I}}^{\prime\prime}q_{selection}</math>的表达式代入该方程得:
| |
|
| |
| <math display="block">
| |
| \mu p=\frac{s p q^{2}}{1-s q^{2}}
| |
| </math>
| |
|
| |
| 若假设''a''等位基因的频率<math display="inline">q</math>较低,则<math display="inline">q^{2}</math>极小,此时<math display="inline">1-s q^{2}</math>可近似为1。该近似导出:
| |
|
| |
| <math display="block">
| |
| \mu \approx s p q^{2}
| |
| </math>
| |
|
| |
| 该式可用基因型频率表示为:
| |
|
| |
| <math display="block">
| |
| q^{2}={\frac{\mu}{s}}
| |
| </math>
| |
|
| |
| 或以等位基因频率表示为:
| |
|
| |
| <math display="block">
| |
| q_{equilibrium}=\sqrt{\frac{\mu}{s}}
| |
| </math>
| |
|
| |
| 因此,在自然选择与突变平衡状态下,有害隐性等位基因的预期频率取决于突变率与选择系数的比值。式7.41表明,即使隐性纯合基因型致死(<math display="inline">s=1</math>),等位基因的预期频率仍为<math display="inline">\sqrt{\mu}</math>,致死基因型的预期频率为<math display="inline">\mu</math>,这源于持续突变的作用。
| |
|
| |
| '''图7.10'''展示了选择与漂变的平衡关系。由突变引起的<math display="inline">\hat{\mathsf{I}}^{\prime\prime}q</math>始终为正,而本例中由选择引起的<math display="inline">\hat{\mathsf{I}}^{\prime\prime}q</math>为负。'''图7.9'''通过取各<math display="inline">\hat{\mathsf{I}}^{\prime\prime}q</math>的绝对值显示两个过程在等位基因频率变化曲线上的交点,此交点即为平衡点。预期平衡等位基因频率为<math display="inline">q_{equilibrium}=\left(\frac{1\mathrm{~×~}10^{-6}}{0.1}\right)^{\frac{1}{2}}=0.0032</math>,与图中结果一致。
| |
|
| |
| 近亲交配相较于随机交配会导致纯合性过剩和杂合性不足。若<math display="inline">f</math>表示偏离哈迪-温伯格预期的程度(见公式2.20),则公式7.41的平衡等位基因频率可重新表述为:
| |
|
| |
| <math display="block">
| |
| q^{2}+f p q=\frac{\hat{\sf{l}}^{1}/4}{s}
| |
| </math>
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/6c80bec01fecfe5961fdc49238eef8f3340790e0d73369dd4628b2950afa6a2d.jpg]]<br />
| |
| '''图7.10''' 隐性纯合子受选择时,由突变引起的等位基因频率变化绝对值<math display="inline">(\hat{\ l}^{\prime\prime}q_{\mathrm{mutation}})^{\star}</math>和自然选择引起的等位基因频率变化绝对值<math display="inline">(\tilde{\Gamma}^{\prime\prime}q_{\mathrm{selection}})</math>。突变持续产生新的隐性等位基因拷贝,而选择持续作用于隐性等位基因的丢失。当突变与选择过程精确抵消时达到平衡等位基因频率。此处参数<math display="inline">s=0.1</math>,<math display="inline">\hat{\mathsf{A}}\mathbf{+}\Theta^{-6}</math>,预期平衡值<math display="inline">q_{equilibrium}=0.0032</math>(垂直箭头所示)。
| |
|
| |
| 假设<math display="inline">q</math>远小于<math display="inline">f</math>,近亲交配下突变与选择达到平衡时的近似平衡等位基因频率为:
| |
|
| |
| <math display="block">
| |
| q_{equilibrium}=\frac{\hat{\sf{l}}^{1}/4}{f s}
| |
| </math>
| |
|
| |
| (参见Haldane 1940;Morton 1971)。由于隐性有害突变仅在纯合状态下受自然选择作用,近亲交配通过增加群体中纯合基因型的比例提高了选择效率。这意味着选择在清除隐性纯合子时更为有效(保护该等位基因的杂合子减少),导致突变-选择平衡时的等位基因频率处于更低水平。反直觉的是,停止近亲交配转为随机交配的群体可能暂时经历有害等位基因频率上升和平均适合度下降,这源于自然选择效率降低。
| |
|
| |
| ==== 遗传负荷 ====
| |
|
| |
| 要使自然选择改变群体中的等位基因频率,某些基因型的个体必须经历更高的死亡率(生存力选择中的实际死亡或繁殖力选择中的生殖失败)。自然选择通过淘汰某些基因型个体并保留其他基因型个体来发挥作用,在此过程中提高平均适合度。与自然选择相关的死亡或生殖失败的总量被称为…
| |
|
| |
|
| |
| -----
| |
|
| |
| <span id="互动框7.5-自然选择与突变"></span>
| |
| === 互动框7.5 自然选择与突变 ===
| |
|
| |
| 您可通过文本模拟网站模拟自然选择与突变的联合作用。在模拟菜单选择”漂变-选择-突变”模型,对话框中设置<math display="inline">N_{e}=20</math>,勾选自然选择选项并设<math display="inline">w_{AA}=W_{Aa}=1.0</math>,<math display="inline">w_{aa}=0.9</math>(或设<math display="inline">s=0.1</math>且A等位基因完全显性),勾选突变选项并设正向突变率为<math display="inline">\hat{\mathbf{\alpha}}^{2}/4\pi\uparrow\tilde{\mathbb{A}}\mathbf{\alpha}^{1}\Theta^{-3}</math>,反向突变率为<math display="inline">\hat{\mathsf{I}}\not\in0</math>。使用公式7.41计算这些参数的预期平衡值后运行模拟。
| |
|
| |
| <pre class="markdown">只要有效种群大小足够大,遗传漂变对等位基因频率结果的影响就微乎其微。你可以通过模拟$N_{e}$值为10、100、500和1000的情况,并比较各情况下的平衡等位基因频率来验证这一预测。
| |
|
| |
| 这个概念最早由Muller(1950)称为"负荷"。遗传负荷有两种形式。替换负荷指在固定有利突变或清除有害突变过程中造成的平均适合度下降。而通过孟德尔式分离在生殖过程中产生低适合度基因型个体的现象,则被称为分离负荷。有性生殖会导致分离负荷,因为重组和自由组合会产生具有不同适合度值的新后代基因型。那些具有较低适合度的后代基因型在生存选择中会消亡(或无法繁殖)。从原理上说,遗传负荷为自然选择改变种群基因型频率的能力设置了上限。由于生存选择导致的死亡数不能大幅超过种群在人口统计学上的冗余个体数(即每代产生的超出种群更替所需的个体数),否则种群将走向灭绝。
| |
|
| |
| 遗传负荷一直被用作估算突变和自然选择过程上限的工具。其中一种研究思路是确定自然选择强度在达到不现实的遗传负荷之前的临界值。替换负荷被用于估算种群中的突变参数,例如有利突变的固定速率、有害突变的发生速率,或与有害突变相关的适合度下降幅度。替换负荷还被应用于设定人体辐射暴露的可接受阈值(Muller 1950; Crow 1997; Lynch 2016),以及理解突变对人类健康的影响。分离负荷则在中性理论早期被用作反对"平衡假说"的反驳依据。在这些应用中,遗传负荷概念一直存在争议(参见Wallace 1991; Crow 1993b的综述)。遗传负荷至今仍在种群遗传学和进化生物学中得到应用,例如解释可能导致小型濒危种群发生突变崩塌的有害等位基因积累(如Lynch和Gabriel 1990),以及论证有性生殖的适合度优势(参见de Visser和Elena 2007的综述)。
| |
|
| |
| 遗传负荷概念(虽然未使用该术语)起源于Haldane的工作(1937)。Haldane的结果可以通过单双等位基因位点的广义显性选择模型来理解,其中相对</pre>
| |
| 【“aottdownsae”译为”崩塌(meltdowns)“】<br />
| |
| 【”äfhe”和”â€fo”识别为排版错误,已根据上下文修正】
| |
|
| |
| 适合度值为 <math display="inline">w_{A A}=1</math> ,<math display="inline">w_{A a}=1-h s</math> ,以及 <math display="inline">w_{a a}=1</math> <math display="inline">-\mathbf{\nabla}S</math> ,其中 <math display="inline">s</math> 是选择系数,<math display="inline">h</math> 是显性系数(见表 6.4)。假设一个处于 Hardy–Weinberg 平衡的群体,具有完全显性(<math display="inline">h=0</math>),且最大适合度为 1。在此类群体中,适合度加权的基因型频率为 <math display="inline">p^{2}</math> ,2pq,和 <math display="inline">q^{2}-s q^{2}</math>。群体的平均适合度即为频率加权的适合度值之和,即 <math display="inline">\overline{{\boldsymbol{\mathsf{W}}}}=\boldsymbol{p}^{2}</math> <math display="inline">+2p q+q^{2}-s q^{2}</math> 。因此,平均适合度为 <math display="inline">\overline{{{w}}}=1-s q^{2}</math> ,因为 <math display="inline">p^{2}+2p q+q^{2}=1</math> 。正向突变(A 到 a)会在每代群体中产生新的隐性等位基因,将一定数量的 Aa 基因型转化为 aa 基因型。假设自然选择与突变处于平衡状态,意味着选择清除 aa 基因型的速率等于突变产生它们的速率。由 Aa 基因型产生新 aa 基因型的速率为正向突变率或 <math display="inline">\hat{\mu}</math>【“f1/4T”可能译为“μ”】。此时群体的平均适合度为 <math display="inline">\overline{{w}}=1-\hat{\mu}/4</math> (假设反向突变可忽略)。在不完全显性(<math display="inline">h\neq0</math>)时,<math display="inline">\overline{{w}}=1-2p q h s -s q^{2}</math> ,且平均适合度可近似为 <math display="inline">\hat{\mu}/2</math>【“w a%。 2 ↑1/4”可能译为“μ/2”】。
| |
|
| |
| 遗传负荷定义为
| |
|
| |
| <math display="block">
| |
| L=\frac{w_{\mathrm{max}}-\overline{{w}}}{w_{\mathrm{max}}}
| |
| </math>
| |
|
| |
| 其表示最大适合度(<math display="inline">w_{\mathrm{max}}</math> ,对应最适基因型)与群体在某一时间点的平均适合度(<math display="inline">\overline{\mathbf{W}}</math>)之间的差异(Crow 1958)。若将 <math display="inline">W_{\mathrm{max}}</math> 定义为 1,则遗传负荷可简化为
| |
|
| |
| <math display="block">
| |
| L=\frac{1-\overline{{w}}}{1}=1-\overline{{w}}
| |
| </math>
| |
|
| |
| 代入 Haldane 的上述结果中的平均适合度,并注意到 <math display="inline">w_{\mathrm{max}}=1</math> ,则完全显性下的遗传负荷为 <math display="inline">L=1-(1-\hat{\mu})/4=\hat{\mu}</math> ,而不完全显性下为 <math display="inline">L=1-(1-2\hat{\mu})/4=2\hat{\mu}/4=\hat{\mu}/2</math>【“2 1%a%d/4”可能译为“2μ/4”】。这预示负荷仅与突变率有关,而与选择系数无关。
| |
|
| |
| 若如 Haldane 所假设,基因座完全独立(无连锁不平衡且无上位效应),则具有多基因座基因型个体的群体平均适合度为所有基因座相对适合度值的乘积:
| |
|
| |
| <math display="block">
| |
| \begin{array}{l}{{\displaystyle{\overline{{{w}}}=\prod_{i=1}^{l o c i}\overline{{{w}}}_{i}=\prod_{i=1}^{l o c i}(1-2\hat{\mu})}}}\ {{\displaystyle{\quad\cong\prod_{i=1}^{l o c i}e^{-2\hat{\mu}}=\prod_{i=1}^{l o c i}e^{-U}}}}\end{array}
| |
| </math>
| |
|
| |
| 其中 <math display="inline">U</math> 是全基因组有害突变率。此时全基因组遗传负荷预计为 <math display="inline">L=1-e^{-U}</math>【“1^{U}$”可能译为“1 - e^{-U}”】。
| |
|
| |
| 直接结论是:更高的突变率会导致更高的遗传负荷,因为自然选择需清除更多有害突变以维持选择/突变平衡。这转化为每一代中必须死亡或无法繁殖的杂合(无完全显性)与纯合个体的比例。负荷永不消失,因为尽管选择从群体中移除有害等位基因,但突变持续供应新的突变。
| |
|
| |
| 后来,Haldane(1957)使用突变负荷的论点来估算替代速率。他这项分析的目标是理解表型演化的速率——当时认为该速率相对缓慢,符合达尔文对渐进变化的强调。Haldane得出结论:自然选择每300代最多只能完成约一次有利替代,且这需要每代个体数量30倍的死亡数。这一结果对群体遗传学领域的部分研究者产生了重大影响。Haldane的结论常被广泛引用为自然选择速率的基本限制。正如Ewens(2004)后来指出的,Haldane的结果隐含假设了人类的人口超额(demographic excess)仅限于群体规模的10%,因此并不像某些人最初认为的那样普适。
| |
|
| |
| '''分离负荷(Segregational load)''':由每代孟德尔分离引入群体中的低适合度基因型个体导致的群体平均适合度下降。<br />
| |
| '''替代负荷(Substitutional load)''':由有害突变的引入或有利突变最终替代导致的群体平均适合度下降。亦称突变负荷(mutation load)。
| |
|
| |
| 为理解分离负荷,假设一个标准双等位基因座的超显性适合度模型,其中''AA''基因型的相对适合度为<math display="inline">1-s</math>,''Aa''为1,''aa''为<math display="inline">1-t</math>(<math display="inline">s</math>和<math display="inline">t</math>为选择系数)。如第6章所示,该自然选择模型的预期平衡等位基因频率为:
| |
|
| |
| <math display="block">
| |
| p_{eq} = \frac{t}{s + t}
| |
| </math>
| |
|
| |
| 和
| |
|
| |
| <math display="block">
| |
| q_{eq} = \frac{s}{s + t}
| |
| </math>
| |
|
| |
| 利用这些平衡等位基因频率,可将平衡选择下预期的杂合体平衡频率表达为:
| |
|
| |
| <math display="block">
| |
| H_{eq} = 2p_{eq}q_{eq} = 2\left(\frac{t}{s+t}\right)\left(\frac{s}{s+t}\right) = \frac{2st}{(s+t)^2}
| |
| </math>
| |
|
| |
| 这表明群体中杂合体的频率取决于针对纯合基因型的选择系数大小。例如,若两种纯合体的存活率均比杂合体低10%(即<math display="inline">s=t=0.1</math>),则平衡时群体中一半个体为杂合体(<math display="inline">H_{eq}=2(0.1)(0.1)/(0.2)^2=0.5</math>)。较弱的选择会导致平衡时杂合度较低,而更强的选择会增加平衡杂合度。
| |
|
| |
| 通过结合平衡时的预期杂合体频率和平均适合度,可得到平衡选择下遗传负荷的表达式(以纯合体选择系数表示):
| |
|
| |
| <math display="block">
| |
| \overline{w} = 1 - \frac{st}{s + t}
| |
| </math>
| |
|
| |
| 如数学框7.2所推导。该群体平均适合度也可通过利用式7.50给出的平衡杂合体频率,转化为由平衡选择维持的杂合度函数。注意到<math display="inline">\frac{st}{s+t} = \left(\frac{2st}{(s+t)^2}\right)\left(\frac{s+t}{2}\right)</math>,因此单基因座的平均适合度可写作:
| |
|
| |
| <math display="block">
| |
| \overline{w} = 1 - H_{eq}\left(\frac{s + t}{2}\right) = 1 - H_{eq}\overline{s}
| |
| </math>
| |
|
| |
| 这个方程具有生物学解释,即平衡选择下处于平衡状态的种群的平均适合度等于1减去平衡杂合度与平均选择系数的乘积。因此,经历平衡选择的种群总是存在一定的遗传负荷,因为平均适合度永远无法达到最大适合度1(杂合体间的交配每代都会产生额外适合度较低的同型合子)。
| |
|
| |
| 让我们使用与1960年代可获得的类似杂合度和选择系数数据,来计算由平衡选择引起的分离负荷。当时在''Drosophila''的同工酶调查估计平均杂合度约为0.3。根据平衡假说,10%的纯合子劣势被认为是合理的,给出选择系数<math display="inline">s=0.10</math>。将这两个值代入式7.52可得平均适合度为:
| |
|
| |
| <math display="block">
| |
| \overline{w}=1-(0.3)(0.1)=1-0.03=0.97
| |
| </math>
| |
|
| |
| <span id="数学框7.2-平衡选择下种群平衡时的平均适合度"></span>
| |
| = 数学框7.2 平衡选择下种群平衡时的平均适合度 =
| |
|
| |
| 要通过纯合基因型的选择系数<math display="inline">s</math>和<math display="inline">t</math>求解平均适合度的方程,首先从平均适合度的标准表达式开始:
| |
|
| |
| <math display="block">
| |
| \overline{w}=p^{2}w_{\mathsf{AA}}+2pq w_{\mathsf{Aa}}+q^{2}w_{\mathsf{aa}}
| |
| </math>
| |
|
| |
| 然后将各基因型的适合度值代入:
| |
|
| |
| <math display="block">
| |
| \overline{w}=p^{2}(1-s)+2pq(1)+q^{2}(1-t)
| |
| </math>
| |
|
| |
| 接着,用选择系数表示的平衡等位基因频率来表达基因型频率(式7.48和7.49):
| |
|
| |
| <math display="block">
| |
| \overline{w}=\left(\frac{t}{s+t}\right)^{2}(1-s)+2\left(\frac{t}{s+t}\right)\left(\frac{s}{s+t}\right)(1)+\left(\frac{s}{s+t}\right)^{2}(1-t)
| |
| </math>
| |
|
| |
| 展开后得到:
| |
|
| |
| <math display="block">
| |
| \overline{w}=\frac{t^{2}(1-s)}{(s+t)^{2}}+\frac{2st}{(s+t)^{2}}+\frac{s^{2}(1-t)}{(s+t)^{2}}
| |
| </math>
| |
|
| |
| 将首项和末项的分子展开:
| |
|
| |
| <math display="block">
| |
| \overline{w}=\frac{t^{2}-t^{2}s+2st+s^{2}-s^{2}t}{(s+t)^{2}}
| |
| </math>
| |
|
| |
| 注意到分子中<math display="inline">s^{2}t+t^{2}s=st(s+t)</math>且<math display="inline">t^{2}+2st+s^{2}=(t+s)^{2}</math>,代入后得:
| |
|
| |
| <math display="block">
| |
| \overline{w}=\frac{(s+t)^{2}}{(s+t)^{2}}-\frac{st(s+t)}{(s+t)^{2}}
| |
| </math>
| |
|
| |
| 化简可得:
| |
|
| |
| <math display="block">
| |
| \overline{w}=1-\frac{st}{s+t}
| |
| </math>
| |
|
| |
| 因此遗传负荷为0.03。当时的同工酶调查还表明,''Drosophila''中约三分之一的基因座存在多个等位基因分离。外推到整个基因组(被认为由约8000afo000个基因座组成),推测可能有2000afo00个可变基因座。若每个基因座完全独立,则全基因组的平均适合度为:
| |
|
| |
| <math display="block">
| |
| \overline{w}=[1-(0.3)(0.1)]^{3000}=(0.97)^{3000}=2.07\tilde{\mathsf{A}}\mathbf{+}\Theta^{-40}
| |
| </math>
| |
|
| |
| 此时分离负荷为<math display="inline">L=1 a@:07 A10^{-40}</math>,接近最大值。这得出遗传负荷将极其巨大的结论。从生物学角度解释,这意味着一个在3000个基因座上杂合的个体需要产生<math display="inline">{10}^{40}</math>个子代(负荷的倒数),才能与在所有基因座上纯合的个体产生一个子代相当。即使使用更低的平均杂合度和选择系数,仍会导致极高的遗传负荷。
| |
|
| |
| <pre class="markdown">分离负荷(segregational load)和替代负荷(substitutional load)在1960年代试图解释物种中分离位点的比例和杂合度水平时发挥了重要作用。平衡选择(balancing selection)曾被考虑并最终被Lewontin和Hubby(1966)拒绝作为解释果蝇属(*Drosophila*)中首个同工酶多态性数据的假说。木村资生(Kimura)在其独立撰写或合作撰写的一系列论文中(Kimura 1960, 1967; Kimura et al. 1963; Kimura and Maruyama 1966)探索并发展了关于替代负荷和分离负荷的理论预期。遗传负荷最终成为木村在其分子演化中性理论(neutral theory of molecular evolution)提案(Kimura 1968)中提出的核心论据之一。木村认为,若所有遗传变化均由自然选择引起,则遗传多态性会过多或分化速率过快,因为由此产生的遗传负荷将过大。木村的替代假说是:许多多态性在选择性上是中性的。中性解释大大降低了遗传负荷,因为只有较小比例的多态性由选择引起并积累遗传负荷。
| |
|
| |
| 对于“自然选择受分离负荷限制”的观点存在一系列反驳(综述见Wallace 1991; Crow 1993b; Ewens 2004第2.11节)。一个批评围绕群体中用于定义最大适应度$W_{\mathrm{max}}$的参考点展开。Haldane和木村将负荷定义为相对于群体中最适应基因型的差异。在平衡选择的情况下,最适应基因型将是所有位点均为杂合的基因型。然而,所有位点均为杂合的基因型出现频率极低。例如,假设所有等位基因频率均为0.5,且适应度由100个对适应度贡献相等的位点决定,则100个位点均为杂合的基因型在随机交配群体中的期望频率为(0.5)$^{100}=7.89\tilde{\mathsf{A}}{\cdot}{\mathbb{H}}^{-31}$。Ewens(2004年综述)指出,若以适应度值高于群体均值(设为1)四个标准差以上的基因型作为参考点(仍为稀有基因型),则$W_{\mathrm{max}}$等于1.98。这意味着最适应个体需要为每个平均适应度个体产生的单个后代生产约两个后代。这种选择成本对许多群体和物种而言似乎是可承受的。</pre>
| |
| 另一个反驳观点聚焦于自然选择在淘汰群体中适应度较低基因型个体时所采取的形式。遗传负荷的估算通常假设每个位点独立,因此自然选择必须独立作用于每个位点的纯合基因型。这等同于假设多个位点间存在乘性适合度关系(在方程7.61中以指数形式体现)。该假设会导致感知到的遗传负荷最大化。事实上,一个个体的选择性死亡可能同时淘汰多个有害等位基因(参见Kondrashov和Crow 1988)。例如,若某个体因在某一位点携带纯合基因型而被选择淘汰,该事件同时也将移除该个体在其他位点携带的任何有害等位基因。类似地,与Haldane的乘性模型相比,上位效应(epistasis)和多效性(pleiotropy)都可能降低遗传负荷。在上位效应中,适合度是多个位点间互作的结果,一个基因型中多个有害突变可能使其适合度值比乘性模型下更快下降,从而被选择更高效地清除。在多效性中,特定位点的基因型影响多个表型,携带有害等位基因的个体死亡可通过提升多个与适合度相关表型的平均适合度来降低负荷。
| |
|
| |
| 另一类关于负荷的研究关注自然选择的作用方式,从而对群体负荷程度提出不同预测。对于完全隐性有害等位基因(h=0),其负荷是部分显性情况的一半,因为每个隐性纯合体的选择性死亡将移除两个有害突变,而杂合体不会死亡。同理,由近亲交配导致的纯合度增加(固定指数F>0)也将降低部分隐性有害等位基因(h>0)的遗传负荷,因为杂合体的选择死亡会减少(Barrett和Charlesworth 1991)。定向选择的截断形式(见图9.10)被建模为替代乘性适合度独立位点假设的方案。在截断选择中,携带低于某阈值数量有害突变的个体会产生类似上位效应的结果——被选择淘汰的个体平均携带的有害突变数量显著多于存活个体(Crow和Kimura 1979,示例见Crow 1997)。该模型显示,截断选择通过每代减少足够数量的平均突变数,可补偿每代新发有害突变的预期数量,从而阻止负荷增长。
| |
|
| |
| 在'''生存力选择'''中,适合度是二元的,被选择淘汰的个体在繁殖前死亡。另一种情况是,选择以繁殖成体间连续适合度变异的形式(如'''繁殖力变异''')起作用,使得适合度在所有存活个体中呈现程度差异。一定程度的'''繁殖力选择'''(替代部分较弱的生存力选择)可能减少替换或分离所需的选择性死亡数量。此时,遗传负荷将表现为不同基因型个体间适合度的变异形式,例如繁殖力变异。这有时被称为自然选择的'''硬性'''(适合度为二元)和'''软性'''(适合度为连续)形式。针对多个非连锁核苷酸位点上发生的弱有害突变的弱净化生存力选择会产生大负荷(Kondrashov 1995)。Charlesworth(2013)展示了两种产生较小负荷的选择形式:一种是对大量位点的弱稳定化选择,其中遗传负荷由个体间因分离核苷酸位点导致的适合度值适度变异产生;另一种是软性净化选择形式,个体通过竞争有限资源实现选择。
| |
|
| |
| 遗传负荷模型的最后一类关注'''种群生态学'''及其与进化变化的相互作用。自然选择的标准模型假设种群无限增长(见第6.1和7.2节)。相反,大多数种群预期表现出'''密度依赖性''',其结果是每代因种内资源竞争导致大量个体死亡。密度依赖引起的死亡可能移除有害等位基因并减轻遗传负荷。密度依赖消除负荷的程度取决于选择淘汰个体的时机——是在它们消耗资源之前还是之后,而这些资源本可用于存活个体的繁殖。若低适合度个体在消耗资源前被选择淘汰,则有害突变通过降低种内竞争能力反而可能增加种群规模,因为剩余资源可供存活个体提高繁殖(Clarke 1973a, b)。类似地,遗传负荷可能影响两个物种的种间竞争,并导致一个物种灭绝——因为选择死亡释放的资源可能被竞争力更强的物种利用(Agrawal和Whitlock 2012)。
| |
|
| |
| 遗传负荷的概念持续推动着突变与选择模型的研究,这些模型试图理解有害突变的命运与潜在积累,尤其是随着实证数据在全基因组有害突变率(''U'')估算方面提供越来越多的证据。
| |
|
| |
| <span id="系谱分支模型中的自然选择"></span>
| |
| ==== 7.4 系谱分支模型中的自然选择 ====
| |
|
| |
| aE系谱分支模型中关于选择的问题
| |
|
| |
| aE定向选择与祖先选择图
| |
|
| |
| aE系谱与平衡选择
| |
|
| |
| 本章的最后一个主题是系统发育分支模型中自然选择的过程。在系统发育分支模型中表示自然选择,需要改变对选择作用方式的理解,并扩展谱系上事件的表示方法。本节的主要目标是引入在谱系上建模选择的方法,以理解自然选择的运作如何改变系统发育树的高度和总分支长度,相较于仅由遗传漂变导致的溯祖模式。
| |
|
| |
| 将自然选择加入系统发育分支模型,给作为基础模型的Wrightaeisher抽样模型带来了重大复杂性。回忆第三章,基础溯祖模型假设当在时间上回溯一代时,任意两个谱系发生溯祖的概率是<math display="inline">\textstyle{\frac{1}{2N}}</math>。这个概率源于以下假设:任何给定世代中的所有谱系在时间回溯时都有同等机会被选为共同祖先。在等位基因选择中性的基础溯祖模型中,当回溯时间寻找最近共同祖先(MRCA)时,每个世代内的谱系具有相等且恒定的概率成为祖先谱系。从时间正向的视角看,在中性演化中每个谱系具有相等的概率被抽样并呈现在下一代中。一般而言,在选择中性条件下,谱系的单倍型不会影响其抽样特性。
| |
|
| |
| 自然选择违背了所有谱系具有相等且恒定溯祖概率的基本假设。当自然选择发挥作用时,由于单倍型相对适合度的差异导致的谱系间适合度差异,某些谱系倾向于随时间增加频率,而其他谱系则倾向于减少频率。这些谱系拷贝频率的变化也转化为随时间变化的溯祖概率。携带受选择偏好单倍型的谱系将随时间增加频率,因此在时间回溯时会具有递减的溯祖概率。类似地,携带较低适合度单倍型的谱系将随时间减少频率,因此在时间回溯时会具有递增的溯祖概率。因此,自然选择与系统发育分支模型内建的抽样过程存在根本性矛盾。
| |
|
| |
| ==== 方向性选择与祖先选择图 ====
| |
|
| |
| 幸运的是,有一种巧妙且相对简单的方法可以修改谱系分支模型以纳入方向性自然选择(Neuhauser 和 Krone 1997;Neuhauser 1999)。这种修改依赖于将溯祖和自然选择视为两个独立的过程,在时间上从现生群体向过去的最近共同祖先(MRCA)回溯时可能发生——正如将溯祖与迁移或突变结合时所用的方法。
| |
|
| |
| 纳入自然选择到谱系分支模型的第一步是稍微改变我们对采样过程的理解。图7.11展示了总数为2N的五个谱系在一个世代中的分布。若存在选择中性,随着时间向前推移,每个谱系会被采样一次以建立下一代群体。这相当于在时间回溯时没有发生溯祖事件。相反,若存在自然选择作用,具有某种单倍型的谱系将被青睐并随时间增加其频率。在图7.11中,自然选择的可能作用通过虚线表示。若以空心圆表示的谱系携带更高适合度的单倍型,它将取代低适合度单倍型的谱系(实心圆)。这种取代事件类似于在群体总数恒定的情况下,高适合度单倍型群体规模的扩张。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/24870c463d9884c4a05305c042477eae1b7783cf7c0a5b56061749d154f495e9.jpg]]<br />
| |
| '''图7.11''' 可能发生溯祖和自然选择事件的单倍体繁殖过程。若无溯祖事件(实线),每个单倍体谱系自我复制并进入下一代。某谱系会产生自身的一个额外拷贝(虚线),并可能取代另一个谱系的一个拷贝。若产生额外拷贝的谱系(空心圆)比随机选择的谱系(实心圆)具有更高适合度的单倍型,它将取代低适合度单倍型的谱系。因此,可能导致自然选择的谱系复制事件结果取决于所涉特定谱系的单倍型状态。实线为延续分支,虚线为输入分支。
| |
|
| |
| 我们可以将延续/输入分支的双重过程视为整体溯祖过程中两个独立的部分。当两个独立过程同时运作时,溯祖模型基于等待任何事件发生,然后判断发生的事件类型。当事件相互独立但互斥时,所有可能事件的发生概率相加得到事件发生的总概率。与处理迁移和突变时相同,我们假设溯祖和自然选择事件是稀有的,或<math display="inline">N_{e}</math>较大且选择系数较小。这一假设确保自然选择和溯祖事件互斥,且当回溯时间发生事件时,该事件只能是溯祖或自然选择中的一种。
| |
|
| |
| 自然选择依赖于较适应单倍型产生迁入分支并取代携带较不适应单倍型谱系的概率。自然选择事件发生率的两倍为
| |
|
| |
| <math display="block">
| |
| \because f=4N_{e}s
| |
| </math>
| |
|
| |
| (<math display="inline">\ddot{|}f</math> 读作 agmaaE,其中 <math display="inline">2N_{\mathrm{e}}s</math> 表示单个谱系在连续时间单位内将发生的自然选择事件期望数(关于此类速率在突变率背景下的完整解释参见第5.节),较适应单倍型的相对适应度为 <math display="inline">1+s</math>,而较不适应单倍型的相对适应度为1。当 <math display="inline">s</math> 为 <math display="inline">\frac{1}{2N}</math> 量级时,自然选择事件的发生率将与中性抽样导致的溯祖事件发生率相当。第 <math display="inline">t</math> 代发生自然选择事件的指数近似概率为
| |
|
| |
| <math display="block">
| |
| P\big(T_{\mathrm{incoming~branch}}=t\big)=e^{-t\underline{{{f}}}
| |
| </math>
| |
|
| |
| 对于单个谱系,以及
| |
|
| |
| <math display="block">
| |
| P\big(T_{\mathrm{incoming~branch}}=t\big)=e^{-t_{2}^{\mathrm{i}}t}
| |
| </math>
| |
|
| |
| 对于连续时间尺度上的 <math display="inline">k</math> 个谱系。自然选择导致的迁入分支在特定时间或之前取代 <math display="inline">k</math> 个谱系之一的概率,可通过累积指数分布近似为
| |
|
| |
| <math display="block">
| |
| P\big(T_{\mathrm{incoming~branch}}\hat{\mathbf{a}}^{9}\not\mathbf{b}\big)\mathbf{p}\rightleftarrows1-e^{-t\frac{\mid}{2}\hat{k}}
| |
| </math>
| |
|
| |
| 这与近似溯祖事件时间的处理方式完全相同。
| |
|
| |
| 将自然选择、溯祖和突变结合为三过程等待时间分布现变得简单。由于这三类事件互斥,我们将自然选择事件发生概率与溯祖或突变事件发生概率相加,得到事件发生的期望等待时间:
| |
|
| |
| <math display="block">
| |
| P(T_{e v e n t}\hat{\mathbf{a}}\%)_{\flat}\mathbf{\bowtie}1-e^{-t\left(\frac{k(k-1)}{2}+\frac{\ddot{\jmath}}{2}k+\frac{\hat{\jmath}}{2}k\right)}
| |
| </math>
| |
|
| |
| 当根据式7.66的等待时间确实发生事件时,需要确定事件类型。由于事件发生的总概率为 <math display="inline">\frac{k(k-1)}{2}+\frac{k\ddot{\mathsf{l}}f}{2}+\frac{k\hat{\mathsf{l}}}{2}</math>,则事件为溯祖的概率为
| |
|
| |
| <math display="block">
| |
| \frac{\frac{k(k-1)}{2}}{\frac{\overrightarrow{k\vert f}}{2}+\frac{k(k-1)}{2}+\frac{k\widehat{\vert}_{,}}{2}}=\frac{k-1}{k-1+\overrightarrow{\vert f+\widehat{\vert}_{,}}}
| |
| </math>
| |
|
| |
| 事件由自然选择导致的概率为
| |
|
| |
| <math display="block">
| |
| \frac{\frac{k\ddot{|}f|}{2}}{\frac{k\ddot{|}f}{2}+\frac{k(k-1)}{2}+\frac{k\hat{|}_{,}}{2}}=\frac{\ddot{|}f|}{k-1+\dot{|}f+\hat{|}_{,}}
| |
| </math>
| |
|
| |
| 事件为突变的概率为
| |
|
| |
| <math display="block">
| |
| \frac{\frac{\mathit{k}\hat{\mathsf{I}}_{\mathrm{,}}}{2}}{\frac{\mathit{k}\hat{\mathsf{I}}f}{2}+\frac{\mathit{k}\left(\mathit{k}-1\right)}{2}+\frac{\mathit{k}\hat{\mathsf{I}}_{\mathrm{,}}}{2}}=\frac{\hat{\mathsf{I}}_{\mathrm{,}}}{\mathit{k}-1+\ddot{\mathsf{I}}f+\hat{\mathsf{I}}_{\mathrm{,}}}
| |
| </math>
| |
|
| |
| 使用方程7.66并确定每个事件是选择、突变还是溯祖,就可以构建所谓的祖先选择图(图7.12)。祖先选择图这一术语用于描述这三个过程的结果,因为它明确显示了可能的自然选择事件。自然选择事件会导致分支的增加,从而可视化单独谱系中不明显的选择事件。当由于自然选择事件(逆时间方向)发生分支时,产生的分支被称为输入分支,以表示可能的谱系替代。输入分支从其分裂出来的谱系被称为延续分支。
| |
|
| |
| 输入分支会在由等待时间分布确定的稍晚时间点与随机选择的谱系发生溯祖,并假定其与溯祖分支的状态。再次参考图7.12以区分输入分支和延续分支。尽管自然选择事件会产生更多分支,但溯祖过程更快并最终会溯祖至MRCA(溯祖速率与<math display="inline">k^{2}</math>成比例,而选择”速率”与<math display="inline">k</math>成比例”)。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/94816d63962cdd8eedec431cfca72966222ae66ee9cd58ad57e7f99dd99a762b.jpg]]<br />
| |
| 图7.12 用于在谱系分支模型中纳入自然选择的祖先选择图。在A中,通过从现生六个谱系逆向推演,确定事件间的等待时间和事件类型直至达到MRCA。由自然选择(虚线)和突变事件引起的分支与溯祖事件被识别。自然选择导致可溯祖谱系数增加一个aioominga6ranch,该输入分支随后可与任何谱系溯祖。在B中,为最终祖先分配单体型状态,并顺时间追踪等位基因状态以确定突变和自然选择事件的结果。在每个选择事件中,比较延续分支和输入分支的状态。本例中A是适应度更高的单体型,当延续分支和输入分支溯祖时会取代a单体型。当延续分支和输入分支的单体型相同时,单体型状态不发生变化。在C中,所有选择事件解决后为现生谱系分配单体型状态。本例中,由于#3处的选择事件取代了较短分支,选择导致总分支长度略有增加。
| |
|
| |
| 图7.12展示了溯祖-自然选择-突变过程的某个结果。图7.12A显示了从现代六个谱系向过去回溯时发生的事件。第一个潜在的自然选择事件(标记为#3,因为按时间正向推进时它是最后发生的事件)发生在谱系2上,导致分支事件。新引入的分支最终与谱系3和4的祖先谱系发生溯祖。
| |
|
| |
| 第二个潜在自然选择事件在谱系5和6的祖先谱系上引发了分支事件。该新引入分支在短时间内再次与同一谱系发生溯祖。最后一个潜在自然选择事件导致来自MRCA附近两个内部谱系之一的分支,与MRCA附近存在的另一谱系发生溯祖。
| |
|
| |
| 这三个选择事件的实际结果只有在确定MRCA的状态和两种单倍型的适合度后才能判定。图7.12B中,祖先被赋予状态''A'',并假设这是较高适合度的单倍型。在祖先选择图中按时间正向推进时,可以确定每个自然选择实例的结果。
| |
|
| |
| 对于选择事件#1,由于突变,新引入分支具有''a''单倍型,而延续分支保持祖先''A''单倍型。由于''A''适合度更高,延续分支的状态被保留,新引入分支的状态被舍弃(这与图7.11中空心圆代表低适合度、实心圆代表高适合度的逻辑完全一致)。在选择事件#2处,新引入分支具有''A''状态,而延续分支因突变具有''a''状态。此时新引入分支取代延续分支,该谱系后续保持''A''状态。在最后的选择事件#3处,新引入分支具有''A''状态,延续分支具有''a''状态,导致延续分支被取代。
| |
|
| |
| 图7.12C展示了解决潜在自然选择事件后的最终谱系结构。给定祖先状态和高适合度单倍型,选择事件#1和#2对树的分支模式没有影响。相比之下,选择事件#3改变了分支模式,将谱系2的溯祖点从延续分支转移到了新引入分支的溯祖点。这反映了自然选择作用后,谱系2通过血统继承与不同谱系产生了同一性。
| |
|
| |
| 这种分支模式的改变使得整棵树的枝长总和比无自然选择时略长。但在此案例中,自然选择并未改变树的高度。
| |
|
| |
| <span id="问题框7.2-解析祖先选择图上的潜在选择事件"></span>
| |
| = 问题框7.2 解析祖先选择图上的潜在选择事件 =
| |
|
| |
| 使用图7.12B并沿时间正向追踪谱系状态,假设MRCA的状态为''a''单倍型且''A''为适应性更强的单倍型。当前谱系状态是否与原图一致?谱系树的高度是否发生变化?作为另一个测试你对祖先选择图理解的练习,假设MRCA状态为''a''等位基因,分别以''A''和''a''等位基因为适应性更强的单倍型来解析图7.12B中的谱系。
| |
|
| |
| 从双等位基因的祖先选择图中得出的结论是明确的。弱到中等强度的定向自然选择通常对平均溯祖时间仅有微小影响。换言之,与具有相同谱系数量的严格中性谱系相比,定向自然选择的作用不会显著改变平均溯祖时间。当选择系数与突变率大致相当时,MRCA的平均时间会略微缩短(Neuhauser and Krone 1997;另见Przeworski et al. 1999)。然而,在有限抽样导致的溯祖时间广泛变异背景下,定向选择与严格中性条件下的平均溯祖时间差异甚微。由于携带强烈不利状态的谱系存在,对有利等位基因的强自然选择或对有害突变的选择预计会降低谱系树的总高度(参见Charlesworth et al. 1993, 1995)。
| |
|
| |
| <span id="互动框7.6-构建祖先选择图"></span>
| |
| = 互动框7.6 构建祖先选择图 =
| |
|
| |
| 构建祖先选择图有助于更好地理解当自然选择、遗传漂变和突变过程共同作用时谱系的演化。你可以使用第5章的Microsoft Excel电子表格扩展版,并修改其以包含自然选择事件。(另有一个R脚本可用于此练习。)该电子表格包含用于确定选择事件、溯祖事件或突变事件的支流分支加入时间的累积指数分布(见式7.48)。为确定给定谱系数<math display="inline">k</math>和突变率下事件发生的时间,需生成0到1之间的随机数并与累积指数分布进行比较。分布中与随机数匹配的时间区间将被视为事件发生时间。下一步是通过比较随机数与各类事件的发生概率来确定事件类型(选择、溯祖或突变),该步骤同样借助式7.49-7.51实现。
| |
|
| |
| 步骤1:打开电子表格,注意黄色高亮字段中设置的关键参数值。你也可点击单元格查看所用公式,特别是每个<math display="inline">k</math>对应的溯祖累积概率。累积概率分布图展示了<math display="inline">k=6</math>和<math display="inline">k=2</math>的情况。
| |
|
| |
| 步骤 2:查看表格右侧标题为 '''Event times''' 的部分。该部分显示了事件发生前的等待时间,并判定事件类型为选择、合并或突变。按下重新计算键(F9、command <math display="inline">\overline{{-}}</math> 或 control <math display="inline">=</math>)生成新的随机数集,观察事件时间的变化。
| |
|
| |
| 步骤 3:从六个初始谱系 <math display="inline">(k=6)</math> 开始,在一张空白纸上绘制包含突变可能的祖先选择图。在纸的底部等距绘制六个点代表六个谱系。
| |
|
| |
| 步骤 4:重新计算表格以生成新随机数。从第一个 '''Decide event time''' 面板开始,确定事件发生前的时间长度(向回溯时间)。接着,根据 '''Decide what type of event''' 的条目判定事件类型为分支引入、合并或突变。若为突变事件,转至步骤 5;若为分支引入事件,转至步骤 6;否则转至步骤 7。
| |
|
| |
| 步骤 5:对于突变事件,首先按等待时间比例沿时间回溯绘制所有谱系的线段(例如,若时间为 0.5,则绘制 <math display="inline">5\mathrm{cm}</math> 的线段)。使用随机数表抽取一个谱系,在事件时间点标记 X 表示突变发生。突变发生后,谱系数量 <math display="inline">(k)</math> 保持不变。转至步骤 4。
| |
|
| |
| 步骤 6:对于引入分支的选择事件,首先按等待时间比例沿时间回溯绘制所有谱系的线段(例如,若时间为 0.5,则绘制 5 cm 的线段)。使用随机数表抽取一个将新增分支的谱系,向左或右绘制虚线水平线表示新谱系分支(该分支将在后续迭代中随时间推移延伸)。为该谱系分配编号 <math display="inline">k+1</math>,并将谱系数量参数 <math display="inline">k</math> 增加 1。转至步骤 4。
| |
|
| |
| 步骤 7:对于合并事件,首先按等待时间比例沿时间回溯绘制所有谱系的线段(例如,若时间为 0.5,则绘制 <math display="inline">5\mathrm{cm}</math> 的线段)。使用随机数表抽取两个将合并的谱系。用水平线连接合并谱系的垂直线段,并将其中一个合并谱系的编号赋予水平线处的共同祖先节点。将另一谱系编号记录于“已消失谱系”列表(后续随机数表中若出现该编号则跳过)。将谱系数量参数 <math display="inline">k</math> 减少 1。转至步骤 8。
| |
|
| |
| 步骤 8:重复步骤 4 直至所有谱系完成合并 <math display="inline">(k=1)</math>。
| |
|
| |
| 步骤 9:为 MRCA 指定等位状态并定义突变模型(例如 <math display="inline">k</math> 等位模型)。同时定义高适应度的等位状态。接着,从 MRCA 开始沿时间正向解析每次突变事件。再次从 MRCA 出发沿时间正向解析自然选择引入的分支,移除携带低适应度单倍型的谱系,保留携带高适应度单倍型的谱系。
| |
|
| |
| 你将得到一个类似于图7.12的祖先选择图(ancestral selection graph)。由于随机溯祖时间和突变时间在其平均值附近波动,你的树形结构会有所不同,但整体形态(例如当<math display="inline">k</math>较大时分支较短)和突变频率(对于给定的突变率)将是相似的。
| |
|
| |
| ==== 谱系与平衡选择 ====
| |
|
| |
| 杂合子具有最高适应度的自然选择(平衡选择的一种类型)也可以被整合到谱系分支模型中(Hudson和Kaplan 1988;Kaplan等 1988;Nordborg 1997;参见Hudson 1990)。本章前文提到,平衡选择预期会在平衡状态下维持双等位基因位点的两个等位基因在种群中持续分离。平衡状态下两个等位基因的频率将取决于针对两种纯合基因型的选择系数。由于单倍体谱系模型不包含二倍体基因型或有性生殖,我们需要采取替代方法而不是指定多个基因型适应度值。
| |
|
| |
| 平衡选择是自然选择中的特例,因为它与遗传漂变导致的固定和丢失作用相反。在谱系分支模型中,遗传漂变由溯祖过程体现。因此,为了近似平衡选择的整体效应,我们需要一个能延迟溯祖程度的过程,使其与二倍体选择模型中杂合子受选择偏好的程度相当。通过将平衡选择建模为具有两个亚群的种群结构,可以获得相同的整体效果。尽管这听起来像一种特殊方法,但种群结构和平衡选择因不同原因会产生相似效应。在结构化种群中,两个谱系除非处于不同亚群,否则无法溯祖(参见图4.23)。因此,将谱系迁移到不同亚群的基因流事件倾向于延迟溯祖事件。基于同样逻辑,我们可以将单一随机交配种群中的平衡选择建模为存在两种谱系类型的过程。类似于基因流(或突变)的转换过程会随机改变谱系类型,同时溯祖过程也在进行。如果两个谱系必须为同类型才能溯祖,那么转换过程将阻止不同类型谱系间的溯祖。
| |
|
| |
| 设两种谱系类型为A和B,其在种群中的频率分别为<math display="inline">p</math>和<math display="inline">q</math>,满足<math display="inline">p+q=1</math>(见图7.13)。每个世代中,一种类型的谱系可能以速率<math display="inline">\upmu</math>转换为另一种类型。种群中总共有2N个谱系,每个世代转换类型的期望数量为<math display="inline">\nu=4N\upmu</math>。转换速率的期望值可作为平衡选择强度的替代指标,因为类型转换将使谱系逃逸溯祖。使用该转换速率,A谱系转换为B谱系的期望等待时间为:
| |
|
| |
| <math display="block">
| |
| P(T_{\mathrm{A\to B}}\leq t)=1-e^{k_{\mathrm{A}}\frac{\nu}{2}\binom{q}{p}}
| |
| </math>
| |
|
| |
| 而B谱系转换为A谱系的期望等待时间为:
| |
|
| |
| <math display="block">
| |
| P\big(T_{\mathrm{B\to A}}\leq t\big)=1-e^{k_{\mathrm{B}}\frac{\nu}{2}\binom{p}{q}}
| |
| </math>
| |
|
| |
| 频率之比(<math display="inline">q/p</math> 和 <math display="inline">p/q</math>)用于调整两类谱系相对频率的指数参数。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/33a92dd42254decff986b094e874642136c4b5074062f454c116b77ed36b22f5.jpg]]<br />
| |
| 图7.13 通过类型转换模拟平衡自然选择的谱系树。每一代中,某一类型(此处为A和B)的谱系会以速率<math display="inline">\upmu</math>转换为另一类型。种群中2N个总谱系每代发生类型转换的期望次数的两倍为<math display="inline">\nu=4N\upmu</math>。由于谱系仅在类型相同时才能发生溯祖,类型转换会延长平均溯祖时间。这与自然选择偏好杂合体的情形类似,因为【“overdominance”译为“超显性”】也会延长等位基因的分离时间。相较于遗传漂变或定向自然选择产生的谱系树,通过类型转换建模的平衡选择所产生的谱系树往往具有更长的分支。
| |
|
| |
| 接下来,我们需要表达等待溯祖事件发生的时间,注意谱系仅在类型相同时才能溯祖。假设有<math display="inline">2N p</math>个A型谱系和<math display="inline">2N q</math>个B型谱系,且溯祖事件互斥,则等待溯祖事件的期望时间为:
| |
|
| |
| <math display="block">
| |
| \begin{array}{r}{P(T_{c o a l e s c e n c e}\leq t)=1-e^{\frac{k_{\mathrm{A}}(k_{\mathrm{A}}-1)}{2}\left(\frac{1}{p}\right)+\frac{k_{\mathrm{B}}\left(k_{\mathrm{B}}-1\right)}{2}\left(\frac{1}{q}\right)}}\end{array}
| |
| </math>
| |
|
| |
| 若类型转换事件与溯祖事件互斥,则各独立指数项可相加得到任意事件的总等待时间:
| |
|
| |
| <math display="block">
| |
| \begin{array}{r}{P(T_{c o a l e s c e n c e}\leq t)=1-e^{\frac{k_{\mathrm{A}}\left(k_{\mathrm{A}}-1\right)}{2}\left(\frac{1}{p}\right)+\frac{k_{\mathrm{B}}\left(k_{\mathrm{B}}-1\right)}{2}\left(\frac{1}{q}\right)+k_{\mathrm{A}}\frac{\iota\left(\frac{q}{p}\right)+k_{\mathrm{B}}\frac{\iota\left(p\right)}{2}}{\left(\frac{1}{q}\right)}}}\end{array}
| |
| </math>
| |
|
| |
| 已知某事件在特定等待时间发生后,可通过在0到1之间生成随机数,并将其与各事件概率除以总概率的累积值比较,从而确定事件类型。
| |
|
| |
| 相较于仅由遗传漂变产生的谱系树(图7.13),通过类型转换建模的平衡选择所产生的谱系树往往具有更长的分支。这是由于谱系类型转换导致溯祖事件间平均等待时间增加。特别地,最后两个谱系的溯祖预计需要更长时间,因为它们必须转换为相同类型。两种等位基因平衡选择的结果与具有亚结构种群的谱系树在最后两个谱系长期等待的特征上具有质态相似性。若突变与平衡选择同时发生,则具有较长分支的谱系树会积累更多突变,因为突变事件数量与谱系树总分支长度成正比。特别值得注意的是,相较于基础中性溯祖模型下的谱系树,两种不同类型的谱系间预计会表现出更多的突变差异。
| |
|
| |
| 对于具有两个以上等位基因且可能杂合基因型具有等效(超显性)适合度值的群体,还存在另一种平衡选择模型(Vekemans and Slatkin 1994; Uyenoyama 1997)。这种多等位基因平衡选择与仅有两个等位基因的平衡选择不同,其谱系在近期的共祖时间较长(或更早时期靠近MRCA的共祖时间较短),与中性谱系相比。多等位基因平衡选择的经典案例是某些植物单一位点自交不亲和性中发现的多个等位基因(如Schierup et al. 1998)。
| |
|
| |
| 第8章将结合遗传多态性模式是否偏离仅由漂变和突变预期的零模型检验,进一步探讨自然选择对谱系形态的影响。
| |
|
| |
| <span id="平衡推移理论"></span>
| |
| ==== 7.5 平衡推移理论 ====
| |
|
| |
| Sewall Wright提出的关于自然选择、遗传漂变、基因流和突变在适应景观上相互作用的经典模型。
| |
|
| |
| 若要选出群体遗传学中影响最为深远的单一模型,Sewall Wright的平衡推移模型及其相关适合度曲面必居前列。Wright最早在1932年第六届国际遗传学大会上提出适合度曲面概念。该会议要求Wright以非数学形式展示其群体遗传学理论工作。Wright试图浓缩其1931年发表的篇幅冗长且数学复杂的重要论文——该论文建立了对众多群体遗传过程的基础性预期。Provine(1986)在Wright传记中指出,作为理解等位基因和基因型频率动态的启发式工具,适合度曲面是”他对现代演化生物学最具影响力的单一贡献”。事实上,适合度曲面至今仍是群体遗传学中广泛使用的隐喻。本节旨在介绍Wright的适应景观隐喻,进而阐释Wright关于遗传漂变、基因流、自然选择和突变在遗传分化群体(即平衡推移过程)中可能如何互动的解释。
| |
|
| |
| ==== 等位基因组合与适合度曲面 ====
| |
|
| |
| 在 Wright 1932年论文的开篇,他首先观察到任何物种中可能存在的基因型数量极其庞大(他称之为“allelomorph combinations”)。他以1000个位点为例:若每个位点有10个等位基因,则组成一个1000位点配子单倍型的可能等位基因组合数为<math display="inline">10^{1000}</math>(Wright指出这是一个惊人的数字,并类比了可见宇宙中电子和质子的估计总数)。接着他假设在这1000个位点中,wild-type等位基因的频率为0.99,而稀有的替代等位基因仅产生与wild-type表型略有差异的性状。
| |
|
| |
| Wright推断:在一个1000位点的单倍型中,种群内表现出由超过20个非wild-type等位基因组合所导致表型的个体比例将极其微小。例如,一个包含20个非wild-type等位基因和980个wild-type等位基因的单倍型预期频率为<math display="inline">(0.01^{20})</math> <math display="inline">(0.99^{980})=5.3\times</math> <math display="inline">10^{-45}</math>,而所有1000个位点均为wild-type等位基因的单倍型预期频率为<math display="inline">0.99^{1000}=4.3\times10^{-5}</math>。全wild-type单倍型的出现频率比含20个非wild-type等位基因的单倍型高40个数量级。
| |
|
| |
| 基于这些假设,单个种群中表现出的表型范围仅能覆盖可能表型范围的极小部分——因为主要由wild-type等位基因构成的单倍型极为常见,而含大量非wild-type等位基因的单倍型极其罕见。Wright由此得出结论:“尽管两个个体拥有完全相同单倍型的概率微乎其微,种群仍被限制在基因组合领域的无限小区域中”。换言之,由于主要由wild-type等位基因构成的单倍型占绝对优势,而含大量非wild-type等位基因的单倍型极为稀有,任何种群中的个体仅能代表庞大可能表型变异范围内的一小部分。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/8c079954c009b995ac102bc289bebb5cf63da1a78a01bd310671289354d02fdd.jpg]]<br />
| |
| 图 7.14 Sewall Wright 提出的原始适应景观图示。适应度曲面的高点以<math display="inline">^+</math>标记,低点以 标记。原图说明:“用二维空间表示数千维基因组合场的示意图。虚线代表适应度的等值线。”来源:改编自Wright(1932)。
| |
|
| |
| 基于对单倍型或配子中大量等位基因组合的认知,Wright继续描述了一个曲面或图景:“如果将特定环境条件下所有可能基因组合的适应值进行分级……”。Wright(1932)提出的适应度曲面如图7.14所示,该图以二维形式呈现至少三维的信息。虽然Wright在原始图中未标注坐标轴,但<math display="inline">x</math>轴和<math display="inline">y</math>轴代表单倍型或基因型中可能的等位基因组合范围。每个基因型的适应度由各点的高度表示(当曲面以二维绘制时,该维度垂直于纸面)。
| |
|
| |
| 在当代用法中,<math display="inline">x</math>轴和<math display="inline">y</math>轴代表等位基因频率(取值范围0到1),而曲面上各点的高度表示对应等位基因频率下种群的均值适应度(Wright的曲面与当代对适应景观【“adaptive landscape”】解释的差异将在本节后续讨论)。虚线表示适应度相等的等高线。曲面的高峰用“<math display="inline">+\gamma</math>”符号标记,低谷用“”符号标记。由于Wright的适应度曲面与标注峰谷的地形图完全类似,“适应景观”这一术语常被用于描述三维图示——其中两个维度表示等位基因或基因型频率,第三个维度表示适应度指标。
| |
|
| |
| Wright 随后考虑了自然选择驱动的演化将如何使种群在这样的适应性地形上移动。他认为存在这样的可能性:“某种特定的[等位基因]组合提供了最大的适应度,而其他组合的适应度会随着移除数量的增加而以某种规律性下降。”用当代术语来说,这相当于'''加性基因作用'''(additive gene action),即基因型值是基因型中等位基因效应的线性函数(参见第9章和第10章)。在加性基因作用下,适合度曲面仅是一个平面,其最高点可以通过种群平均适合度逐步提升的中间步骤达到。另一方面,Wright也设想了存在“…两个峰值…”的适合度曲面。具有多峰值的适合度曲面源于显性作用和'''上位效应'''(epistasis),这类基因作用能通过微小的等位基因组合变化引发平均适合度的巨大改变,因为基因型值是基因型中等位基因效应的非线性函数。Wright推测“在这种崎岖的地形中,选择能轻易将物种带到最近的峰值,但可能存在无数更高的峰值,它们被‘低谷’所分隔。”(第7章展示了严格加性、显性和上位效应下的适合度曲面实例。)
| |
|
| |
| 通过Wright的适应性地形图,可以直观地看到仅依赖自然选择推动演化改变的一个基本挑战。自然选择的作用是基于种群当前等位基因频率位置周围适应性地形的即时斜率来提升种群的平均适合度。这将导致等位基因频率的变化——若不受其他过程阻碍——最终通过持续在适应性地形上的上行移动达到可实现的最高平均适合度。潜在的问题在于:选择在引起代际间等位基因频率变化时,并未对适应性地形进行全局性观察。自然选择过程仅能“感知”种群当前等位基因频率空间位置周围适应性地形的即时斜率。若适应性地形存在多个峰值,仅靠选择过程可能使种群“滞留”在曲面上的局部平均适合度最大值点,而非可能的最高平均适合度水平。用地形隐喻来说,自然选择如同登山者必须始终向上攀爬,既不能下降(即使是暂时性的)也无法穿越山谷。由于这种适合度持续提升的要求,自然选择可能无法到达适合度曲面上的最高峰。
| |
|
| |
| <span id="wright关于等位基因频率分布的视角"></span>
| |
| ==== Wright关于等位基因频率分布的视角 ====
| |
|
| |
| 在描述了适应度表面的隐喻并询问何种机制可能克服自然选择的局限性后,Wright试图总结他当时关于等位基因频率分布形态的研究——这些分布在种群遗传学基本过程的作用下预期会出现。他在总共三个段落中非常简洁地总结了这些思想,未引用任何方程,仅参考了一张图(见图7.15)。
| |
|
| |
| 图7.15A的三个面板描述了整个物种中许多独立复制的有限种群内,单个位点的等位基因频率预期平衡分布。自然选择、遗传漂变和突变的过程同时作用以塑造这些等位基因频率分布。当4NU(等同于θ)和4NS(有效种群大小与选择系数乘积的四倍)较大时(图7.15A左面板),独立种群间等位基因频率的分布较窄。这种分布源于对野生型等位基因(S用实箭头表示)较大的选择系数,以及相对较弱的遗传漂变(虚线箭头标记为<math display="inline">\frac{1}{4N}</math>,其中<math display="inline">N</math>为有效种群大小)。频繁的正向突变(<math display="inline">U</math>用实箭头表示)阻止了野生型等位基因的完全固定,使分布向左偏移。较低的反向突变率(<math display="inline">V</math>用虚线箭头表示)略微增加野生型等位基因的频率,使分布向右偏移。
| |
|
| |
| 当4NU和4NS取中间值时(图7.15A中面板),独立种群间等位基因频率的分布较宽。在这种情况下,选择、突变和遗传漂变的作用力(均为实箭头)大致相等,因此复制种群表现出一定范围的野生型等位基因频率。在图7.15A右面板中,当4NU和4NS较小时,由于遗传漂变较强(<math display="inline">\textstyle{\frac{1}{4N}}</math>用实箭头表示)而自然选择和突变(<math display="inline">S</math>、<math display="inline">U</math>和<math display="inline">V</math>用虚线箭头表示)较弱,等位基因频率的分布呈马蹄形(大多数复制种群接近固定或丢失)。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/12337188763ce229e83741e2a2565504d0b078d5166250668ba5ed1df7da1ba8.jpg]]
| |
|
| |
| 图7.15 Wright对多种群体遗传过程同时作用导致等位基因频率均衡分布的示意图解。每个分布代表多个重复群体或集合分布的等位基因频率(在A中,组成物种的众多群体是独立的,而在B中,亚群体通过岛屿模型相互依存)。各过程对等位基因频率分布影响的大小和方向由带字母的箭头表示。实线箭头表示较强过程,虚线箭头表示较弱过程。例如,在B板块最左侧的分布中,相对于漂变的强迁移使亚群体等位基因频率保持较小分化,而弱【“genetic leads”译为“遗传主导”】导致亚群体等位基因频率围绕总群体平均频率呈现适度扩散。所有板块中,野生型等位基因频率(x)显示在x轴,具有特定等位基因频率的群体频率显示在y轴。y轴的概率由A和B顶部的方程给出,该方程基于群体参数值计算x轴上的等位基因频率。原图注:“不同指定条件下基因频率的随机变异。”来源:引自Wright(1932)。
| |
|
| |
| 图7.15B的三个板块描述了由一定程度的基因流连接的多个有限亚群体中,单个位点的等位基因频率均衡分布。此时决定等位基因频率分布的力是遗传漂变(标有<math display="inline">\textstyle{\frac{1}{4n}}</math>的箭头,其中n为亚群体的有效群体大小)和迁移(标有m的箭头,表示岛屿模型中的迁移率)。这里Wright假设迁移远强于突变和选择,因此后两个过程可忽略。在图7.15B左板块的极端情况下,当<math display="inline">4n m</math>较大时(由于高迁移率(实线箭头)和/或大有效群体尺寸导致的弱遗传漂变(虚线箭头)),亚群体间等位基因频率分布较窄。图7.15B中间板块显示遗传漂变与迁移近似平衡时,亚群体中等位基因频率呈现广泛的中频分布。另一极端如右板块所示,当<math display="inline">4n m</math>较小时(由于低迁移率和/或小有效群体尺寸导致的强遗传漂变),等位基因频率分布呈马蹄形(多数群体接近固定或丢失)。
| |
|
| |
| ==== 赖特设想的演化情景 ====
| |
|
| |
| 在等位基因频率分布确定后,Wright转而研究不同自然选择、突变、遗传漂变和迁移参数下种群在适合度曲面上的运动。Wright认为景观中种群的位置、种群在景观上占据的区域以及景观地形本身都会随时间变化。他的目标是通过足够的试错(或遗传漂变)来阐明克服自然选择将种群限制在单一适合度峰值的可能性。图7.16展示了Wright考虑的六种可能情形。在这六种情形中,图7.15的等位基因频率分布定义了种群或繁殖群(deme)内个体间预期适合度变异的范围。
| |
|
| |
| 这种关联源于当图7.15中等位基因频率分布的每个位点被解释为具有表型效应时,野生型等位基因纯合基因型具有最高适合度。更宽的等位基因频率分布会导致更多可能的等位基因组合,从而产生更广的适合度值范围。
| |
|
| |
| 图7.16中的A、B组展示了Wright关于大4NS和4NU值背景下物种在适应性地形(adaptive landscape)上占据区域的观点。假设种群最初占据适合度峰值周围的某个区域(如图7.16A中阴影圆内的虚线圆所示),若针对非野生型等位基因基因型的选择系数降低或正向突变率增加,种群在适应峰周围占据的区域将会扩展(更大的阴影圆)。这对应于等位基因频率分布从图7.15A左图变为中间图的情形。相反,当针对非野生型等位基因的选择加强或正向突变率降低(在大4NS和4NU背景下),种群占据的适合度曲面区域会因等位基因频率分布范围变窄而收缩(对比图7.16B中虚线圆与更小的阴影圆)。这种情况对应于等位基因频率分布从图7.15A中间图反向变为左图的情形。在图7.16A情形中,物种的平均适合度降低,使得”被占据的[适合度曲面]场域可能扩展到包含另一个更高峰值…“或跨越适合度谷成为可能。若种群发生有利突变并通过选择固定,适合度峰值本身也可能升高。但Wright指出突变率非常低,因此这类进化变化会极为缓慢。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/d3caa32f3c0704e459fccba55661bb3965178428957f0fa2d246ab4891d54115.jpg]]
| |
|
| |
| 图 7.16 Wright 对漂变-突变平衡(由 4NU 的强度决定)、漂变-选择平衡(由 4NS 的强度决定)以及岛屿模型中的漂变-迁移平衡(由 <math display="inline">4n m</math> 的强度决定)作用的图示。Wright 的参数包括:有效种群大小 N、突变率 U、定向选择中的选择系数 S,以及无限岛屿模型中的有效迁移率 4 nm。“近交”(inbreeding)一词在此指种群层面因有限种群大小导致遗传漂变的现象。原图注:“种群在可能基因组合的广义场中所占据的基因组合场。特定条件下历史类型的特征通过其与初始场(粗虚线轮廓)及箭头的关系表示。”来源:改绘自 Wright (1932)。
| |
|
| |
| Wright 还考虑了适应性景观本身的形态如何可能发生变化。图 7.16C 展示了 Wright 关于适应性景观如何随时间因种群环境背景变化(仍假设 4NS 和 4NU 为较大值)而改变的概念。由于基因型适合度值由物种所处的物理和生物环境定义,等位基因组合的适合度值很可能随时间改变。这将导致适合度曲面自身的重塑——适应性景观上的峰谷高程变化或峰的位置随时间推移发生位移。尽管这种适合度曲面的变化会使种群追踪高适合度峰,但 Wright 认为这是“无适应进步的变迁”,因为种群未必占据适合度景观中的多个峰,也未必向更高平均适合度的方向演化。
| |
|
| |
| Fisher(1999 年校勘版)强调了这一主题:持续的环境变化驱动种群中最高适合度基因型的不断重新定义。在此视角下,崎岖的适应性景观问题较小,因为种群可被视为占据等位基因频率空间的一个区域,而该区域内适合度高程的地形会随时间改变。如果适合度景观持续重塑,种群就不会被困在某个适合度峰上——最终这个峰本身也会移动或改变位置。这一观点也是 Van Valen(1973)提出的“红皇后”或“军备竞赛”模型的基础。该模型认为,物种必须不断经历适应性变化以跟上持续变化的基因型适合度值,而这些变化本质上源于由其他物种(其自身也在不断变化)定义的永恒变化的环境背景。
| |
|
| |
| Wright考虑的另一种可能性,如图7.16D和E所示,聚焦于有效种群大小。他指出,如果有效种群大小相对于选择系数和突变率非常小(图7.16D),种群很可能因遗传漂变在所有位点经历固定或丢失(参见图7.15A右侧面板中的等位基因频率分布)。其结果是,种群将停止向适应峰的吸引,会在适应度景观中随机游走,并经历有害等位基因的固定导致近交衰退【“inbreeding depression”译为”近交衰退”】。如果有效种群大小迅速减小,那么在大多数位点完成固定和丢失后,景观上的移动将变得非常缓慢,因为大多数新突变不太可能长期维持分离状态。
| |
|
| |
| 相比之下,具有中等有效种群大小(相对于选择系数和突变率而言)的有限种群(图7.16E)将在表面上占据相当大的区域,会经历围绕适应峰的随机移动,但不会偏离峰顶太远。这种情况发生的原因是种群将在自然选择和遗传漂变之间达到近似平衡,并随时间推移获得新突变的输入(参见图7.15A中间面板中的等位基因频率分布)。Wright认为经历遗传漂变、自然选择和突变平衡(4NU和4NS的中等值)的种群能够转换适应峰,这是”物种可能通过这种方式攀登至整个领域的最高峰”的途径。其局限性在于,Wright预计单个种群实现峰转换将是一个非常缓慢的过程,只有当突变率近似等于有效种群大小的倒数时才会发生。
| |
|
| |
| Wright 所考虑的最后一个案例(如图7.16F所示)是物种被划分为多个有限的地方种群(或“小型地方种族”),这些种群几乎处于遗传隔离状态但仍存在一定基因流的情况。此时,Wright关注的是图7.15B中间面板显示的等位基因频率分布——在导致种群分化的遗传漂变和导致等位基因频率均质化的基因流之间达到平衡,从而在地方种群间形成广泛的等位基因频率分布。
| |
|
| |
| Wright的观点是:与单一随机交配种群相比,多个半独立的有限地方种群在适应度景观上的位置移动会更为迅速。他进一步推测那些达到更高适应度峰值的种群会产生更多迁移个体。迁移个体数量增加的效应将表现为:处于更高适应度峰值的种群会通过迁移改变接收这些迁移个体的其他种群的等位基因频率,使其趋向更高适应度峰值的位置。这种来自高适应度峰值种群的更高基因流速率过程常被称为'''群间选择'''(interdemic selection),因为它等同于自然选择在具有不同群体繁殖力水平的地方种群层次上发挥作用。
| |
|
| |
| 因此,Wright设想:由多个细分地方种群组成的物种若承受近似相等的自然选择压力和遗传漂变压力,将能探索更多的适应度表面,相比单纯依靠自然选择更可能发现更多高适应度峰值。他总结道:“将物种细分为地方种族,为基因组合领域的试错过程提供了最有效机制。”
| |
|
| |
| 这种'''动态平衡过程'''(shifting balance)常被概括为细分种群中三个“阶段”的同步运作:<br />
| |
| - '''第一阶段'''涉及地方种群内的遗传漂变,导致每个种群的等位基因频率位置相对于适应度峰值发生随机偏移;<br />
| |
| - '''第二阶段'''是自然选择对地方种群的作用,使种群的等位基因频率位置向更高适应度峰值移动,且更高的峰值对等位基因频率产生更强影响;<br />
| |
| - '''第三阶段'''为群间选择,此时种群的迁出率与其平均适应度成正比。因此,处于更高适应度峰值的种群输出更多迁移个体,并在其他种群的迁入群体中占据更大比例,从而推动所有种群的等位基因频率向更高适应度峰值的位置移动。
| |
|
| |
| ==== 关于动态平衡理论的批评与争议 ====
| |
|
| |
| 尽管Wright的适应性地形隐喻和shifting balance理论提议激发了生物学家数十年的思考,但他的观点也引发了持续的争议。适合度表面隐喻本身一直是批评的焦点,因为Wright最初描述的适合度表面在某些方面存在问题。正如Provine(1986)所述,Wright使用了两种截然不同的适合度表面版本。其中一个版本基于基因型中等位基因组合的排序来展示每个基因型的适合度。在这个版本的适合度表面中,每个等位基因组合都具有相对适合度,并定义地景上的一个点。这种类型的表面被比作构成照片印刷或数字图像的像素(Ruse 1996)。在基因型版本的适合度表面中,除代表适合度的维度外,其他维度的生物学意义并不明确,因为基因型轴与种群中基因型或等位基因的频率无关。
| |
|
| |
| 另一个版本的适合度表面绘制了种群在所有可能等位基因频率下的平均适合度。当代对适合度表面隐喻的使用通常采用种群平均适合度的概念,其中坐标轴代表等位基因频率,一个维度代表种群在这些等位基因频率下的平均适合度——尽管存在例外(如Weinreich等,2005)。Wright在著作中经常在这两种适合度表面类型之间来回切换,导致歧义和混淆(Provine 1986)。自Wright的工作以来,适合度表面已被以多种方式构建和解释(Gavrilets 2004;Skipper 2004)。
| |
|
| |
| Coyne等(1997)对Wright的shifting balance理论提出了详尽而有力的批评,他们检视了支持与反对该理论三阶段在真实种群中运作的证据。他们借助60多年来群体遗传学理论研究的成果重新审视了shifting balance理论的理论基础,并考虑了关于适合度表面形态和shifting balance过程各阶段运作的经验证据。他们的结论是:“尽管存在支持shifting balance过程个别阶段的证据,但很少有经验观察能通过Wright的三阶段机制获得比简单大群选择更好的解释”。
| |
|
| |
| 其他作者为shifting balance理论辩护或提出了替代观点(如Wade和Goodnight 1998;Peck等1998),引发了一系列的回应与反回应(Coyne等2000;Goodnight和Wade 2000;Peck等2000)。虽然在此无法详细探讨该辩论中提出的所有观点,但对shifting balance过程要素的分歧凸显了当多个群体遗传过程同时运作时,试图预测其结果所面临的困难。
| |
|
| |
| 迁移平衡过程的第三阶段,即根据种群平均适合度按比例产生迁移个体,并通过差异贡献形成移民库从而实现种群群的转移,尤其存在问题(见 Crow 等人 1990)。难点在于迁移率必须足够低以维持种群划分为半隔离的种群群(deme),同时又要足够高以允许亚种群间个体(或配子)的交流,从而实现种群群间选择(interdemic selection)。一个普遍的反对意见是:种群群间选择是群体选择(group selection)的一种形式,即某个个体群体相对于其他群体具有更高的存活率或繁殖率,导致某些种群灭绝而另一些种群持续扩张的过程。Williams(1966, 1992)提出的经典论点认为,针对个体基因型间加性遗传变异(additive genetic variation)的自然选择预期比群体层面的选择作用更快,因为个体频率的变化速率可以比种群频率的变化快得多。尽管如此,在差异迁移背景下群体选择可能存在的证据已通过赤拟谷盗(''Tribolium castaneum'')实验得到展示(Wade 和 Goodnight 1991;Wade 2013)。通过根据种群总个体数选择下一代奠基个体,研究人员在九代间观察到了种群个体数量的巨大变化。与之相反,当奠基个体的选择与种群大小无关时,种群规模随时间推移未发生改变。对此类赤拟谷盗实验(Goodnight 和 Stevens 1997 综述)的解释一直存在争议,因为学界对群体选择与个体选择的界定标准以及实验程序所施加的选择类型存在分歧(见 Coyne 等人 1997;Getty 1999;Wade 等人 1999)。作为第三阶段的支持证据,Bitbol 和 Schwab(2014)使用单倍体模型和模拟表明,种群细分可以加速适合度低谷和高原的跨越。
| |
|
| |
| 关于平衡转移理论争议的另一面涉及上位性(epistasis)概念的双重性质(见Cheverud和Routman 1995;Whitlock等1995;Fenster等1997;Brodie 2000;Cordell 2002)。当两个或多个位点的基因型产生的基因型值大于或小于各基因座单独作用时的基因型效应之和时,即存在上位性(见第9章)。两个或多个基因座间相互作用的存在表明存在生理上位性(physiological epistasis,也称为功能性或机制性上位性)。生理上位性这一术语仅指两个或多个基因座的特定基因型在表型形成中的相互作用。这种生理上位性对群体水平参数的贡献(若有)取决于群体中相互作用基因型的频率。
| |
|
| |
| 统计上位性(statistical epistasis)这一术语用于指代由基因座间相互作用引起的群体基因型值现存变异的量。在第9章和第10章的符号和概念中,统计上位性即<math display="inline">V_{I}</math>。群体中存在的统计上位性量是相互作用多基因座基因型频率的函数,因此也是群体等位基因频率的函数——正如加性方差(<math display="inline">\mathrm{{}}V_{A}</math>)和显性方差(<math display="inline">{\cal V}_{D}</math>)的情况,同时也受交配系统和重组率的影响。
| |
|
| |
| Wright默认假设统计上位性在自然群体中普遍存在。虽然有证据表明自然群体和实验室群体中存在统计上位性(MacKay 2001;Cordell 2002;Carlborg和Haley 2004;见Wolf等2000的章节),但统计上位性在群体中并不广泛存在,尽管其仍难以准确估计。目前关于上位性对整体数量性状变异的相对贡献尚未达成共识,但已认识到上位性的实证检测受实验设计和统计功效的限制(见Whitlock等1995)。有结论认为缺乏证据表明自然群体中存在强烈或频繁的统计上位性。另一些观点则认为自然群体中存在上位性的某些证据,且由于上位性难以检测,对其普遍性下结论为时尚早。这些不同观点使得总结具有遗传变异的群体中适应性景观的本质变得困难。
| |
|
| |
| 当群体处于所有位点的固定和丢失状态时,即使存在生理上位效应且可能非常强烈,也不会存在统计上位效应,因为基因型值没有变异。对于可能表现出极少统计上位效应但具有丰富生理上位效应的群体,另一种上位效应的定义是有用的。符号上位效应是生理上位效应在具有极少或没有遗传变异的群体中的特例(Weinreich et al. 2005)。当一个新突变在某些由其他位点定义的遗传背景上表现出高于平均的适应度,而在其他遗传背景上表现出低于平均的适应度时,该位点即表现出符号上位效应。因此,适应度值的符号是该等位基因遗传背景中其他位点的函数。Weinreich et al. (2006) 研究了细菌<math display="inline">\upbeta</math>-内酰胺酶基因的五个单核苷酸突变。其中四个突变导致<math display="inline">\upbeta</math>-内酰胺酶基因的错义版本,因此它们在抗生素环境中单独存在时是有害的并被选择对抗。第五个突变是基因<math display="inline">5^{\prime}</math>端的非编码区变化。然而,当所有五个突变同时发生时,它们会产生一种能赋予对<math display="inline">\upbeta</math>-内酰胺类抗生素(如青霉素)耐药性的<math display="inline">\upbeta</math>-内酰胺酶基因版本。当每个突变出现在已携带其他四个突变的遗传背景上时,其适应度为正,因为具有五个突变的基因版本在抗生素环境中具有高适应度。一般而言,符号上位效应预测某些等位基因组合可能只有有限数量的突变组合能导致适应度增加。
| |
|
| |
| 适应度景观概念仍然与演化生物学中的许多问题相关,例如通过众多演化中间步骤产生的表型的可重复性程度(参见 de Visser 和 Krug 2014 年、Fragata 等 2019 年的综述)。Yi 和 Dean (2019) 提出,通过实验改变和理解核苷酸及氨基酸变化如何以及为何改变分子表型的近因细节的新兴能力,将导致经验定义的适应度景观,从而解释演化轨迹。他们回顾了七项示例性研究,其中将遗传变异的观察与实验工作相结合,以理解由个体基因型变化引发的基因型到表型再到适应度的路径。能够通过高度特异性的实验基因型改变产生表型和适应度变异(如 Karageorgi 等 2019)的技术进步是一项突破,似乎可能推动更多关于定义基因型-表型-适应度因果路径的实证研究,并深化对适应度景观的理解。
| |
|
| |
| <span id="第7章-综述"></span>
| |
| = 第7章 综述 =
| |
|
| |
| 群体的平均适应度可以视为按基因型或等位基因频率绘制的平均适应度图,称为适应度曲面。自然选择在适应度曲面上扮演上坡攀登者的角色,根据当前基因型频率处的斜率将基因型频率向上移动。如果存在显性或上位效应,适应度曲面将具有多个峰谷。
| |
|
| |
| 当适合度取决于单一位点的三个等位基因时,若存在强烈的超显性和亚显性现象,自然选择的结果将依赖于种群初始基因型频率。重组与自然选择的净平衡可能导致均衡状态无法对应平均适合度的最大值。重组趋向于配子平衡的建立,与平均适合度无关,且可能与自然选择作用方向相反。虽然生存力模型常被用作适合度的标准范式,但当适合度被定义为繁殖力差异、环境容纳量差异,或当适合度值随时间空间变化时,基因型频率及其均衡状态的变化模式往往显著不同。当自然选择与遗传漂变共同作用时,若<math display="inline">4N_{e}s</math>远大于1则选择相对漂变占优;若<math display="inline">4N_{e}s</math>远小于1则漂变相对选择占优;当<math display="inline">4N_{e}s</math>近似等于1时二者作用强度相当。
| |
|
| |
| 当自然选择与突变共同作用时,有害等位基因将在种群中维持一定水平,其平衡频率随突变率增加而上升,随近交程度增加而上升,但随纯合状态下的选择系数增加而下降。
| |
|
| |
| 遗传负荷源于自然选择作用下突变或基因型频率改变时必须发生的选择死亡(生殖或实际死亡)。理论上,自然选择的强度受限于种群在免于灭绝前提下所能承受的遗传负荷阈值。遗传负荷相关论证曾被用作分子进化中性理论的间接证据。
| |
|
| |
| 相较于Haldane-Muller模型的预测,遗传负荷的测算高度依赖于作为<math display="inline">w_{\mathrm{max}}</math>参考基准的基因型选择,并可能通过以下途径降低:有害突变表现为隐性性状;同源血统纯合度提升;或截断选择、平衡选择、柔性选择机制的作用。
| |
|
| |
| 在谱系分支模型中,定向选择可建模为祖先选择图。弱定向选择总体上不会显著改变谱系树的总枝长与总高度。
| |
|
| |
| 在谱系分支模型中,平衡选择可建模为类群转换过程(类似基因流或突变)。对于双等位基因系统,平衡选择会延长最后两个谱系支系的溯祖时间,因其必须转换为相同类型才能溯祖。对于三个及以上等位基因系统,平衡选择倾向于增加溯祖时间并延长谱系树末端分支。
| |
|
| |
| Sewall Wright提出的适应景观隐喻是一种启发式工具,旨在阐释单纯自然选择过程的局限性——因其仅能提升种群平均适合度。平衡转移理论假说认为,自然选择、遗传漂变、突变和种群亚结构的同时作用,可能使种群探索适应景观的区域范围超越单纯选择机制所能达到的范畴。
| |
|
| |
| 适应景观作为种群遗传学中的经典隐喻,在精准基因型编辑的表型效应与适合度效应实验研究中正焕发新的理论价值。
| |
|
| |
| <span id="延伸阅读-2"></span>
| |
| = 延伸阅读 =
| |
|
| |
| 关于双位点选择(以适合度曲面为特征)的经典且易于理解的论述,可参考:
| |
|
| |
| Lewontin, R.C. 和 White, M.J.D. (1960). Interaction between inversion polymorphisms of two chromosome pairs in the grasshopper, ''Moraba scurra''. ''Evolution'' 14: 116–129.
| |
|
| |
| 涉及两位点或更多位点上影响适合度的基因型互作案例研究、视角与基础理论,参见以下著作的章节:
| |
|
| |
| Wolf, J.B., Brodie, E.D. III, 和 Wade, M.J. (编) (2000). ''Epistasis and the Evolutionary Process''. Oxford: Oxford University Press.
| |
|
| |
| 对基础存活自然选择模型的扩展(涵盖适合度的时空变异、适合度权衡、竞争与捕食等生物学变异)可参考:
| |
|
| |
| Roff, D.A. (2001). ''Life History Evolution''. Sunderland, MA: Sinauer Associates.
| |
|
| |
| 关于采用<math display="inline">F_{ST}</math>离群值方法检验局部适应经验的实证研究综述,见:
| |
|
| |
| Haasl, R.J. 和 Payseur, B.A. (2016). Fifteen years of genomewide scans for selection: trends, lessons and unaddressed genetic sources of complication. ''Molecular Ecology'' 25: 5–23.
| |
|
| |
| 对遗传负荷经典模型及拓展该领域理解(涉及有害等位基因与自然选择关系)的近期模型综述:
| |
|
| |
| Agrawal, A.F. 和 Whitlock, M.C. (2012). Mutation load: the fitness of individuals in populations where deleterious alleles are abundant. ''Annual Review of Ecology, Evolution, and Systematics'' 43: 115–135.
| |
|
| |
| 关于原始适合度曲面的背景解释及其对批评的回应,参见:
| |
|
| |
| Wright, S. (1988). Surfaces of selective value revisited. ''American Naturalist'' 131: 115–123.
| |
|
| |
| <span id="章末习题-1"></span>
| |
| = 章末习题 =
| |
|
| |
| 1 参考表7.1顶部组的相对适合度值及图7.2的适合度景观。若种群中仅存在A和S等位基因,在无限种群中自然选择预期的平衡等位基因频率是多少?
| |
|
| |
| 2 参考表7.1顶部组的相对适合度值。假设C等位基因初始频率为0.001(仅受突变压力时的极高频率)。一代遗传漂变是否可能使C等位基因达到足够高的频率,从而通过自然选择继续增加?首先,计算C等位基因在低频率范围(尝试<math display="inline">r=0.001{-}0.1</math>)下受自然选择的频率变化(即<math display="inline">\Delta r</math>,以<math display="inline">r</math>表示C等位基因频率)。根据<math display="inline">\Delta r</math>,C等位基因需达到何种最低频率才能被自然选择推动增加(<math display="inline">\Delta r>0</math>)?
| |
|
| |
| 遗传漂变是否足以使C等位基因频率跨越适合度景观谷值(即<math display="inline">\Delta r>0</math>)?估算有效种群大小为100、10和2时,C等位基因频率在遗传漂变下的预期方差。使用二项分布估算有限抽样导致的等位基因频率变化方差。
| |
|
| |
| 使用电子表格或代码计算<math display="inline">\Delta r</math>将便于比较多组参数值。
| |
|
| |
| = 习题框答案 =
| |
|
| |
| == 习题框7.1答案 ==
| |
|
| |
| <math display="block">
| |
| \begin{array}{c l c r}{{W\mathsf{A A}=0.679~w_{\mathsf{A S}}=0.763~w_{\mathsf{S S}}=0.153~w_{\mathsf{A C}}}}\ {{\qquad=0.679~w_{\mathsf{S C}}0.534~w_{\mathsf{C C}}=1.0}}\end{array}
| |
| </math>
| |
|
| |
| 初始等位基因频率设置1:
| |
|
| |
| <math display="block">
| |
| \overline{{w}}=0.679(0.75)^{2}+0.153(0.2)^{2}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| +1\left(0.05\right)^{2}+(0.763)2(0.75)(0.2)
| |
| </math>
| |
|
| |
| <math display="block">
| |
| +(0.679)2(0.75)(0.05)+(0.534)2(0.2)(0.05)
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \overline{{w}}=0.382+0.00612+0.0025+0.2289+0.051
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \overline{{w}}_{C}=1(0.05)+(0.679)(0.75)+(0.534)(
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{0.05(0.6661-0.6812)}{0.6812}}=-0.0011
| |
| </math>
| |
|
| |
| C等位因边际适应度低于平均适应度而趋于丢失。
| |
|
| |
| <math display="block">
| |
| \overline{{w}}=0.679\left(0.7\right)^{2}+0.153\left(0.2\right)^{2}+1\left(0.1\right)^{2}
| |
| </math>
| |
|
| |
| <math display="block">
| |
| +(0.763)2(0.7)(0.2)+(0.679)2(0.
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \overline{{w}}=0.333+0.0061+0.01+0.2136+0.0951
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \overline{{w}}_{C}=1(0.1)+(0.679)(0.7)+(0.534)(0.2)=0.6821
| |
| </math>
| |
|
| |
| <math display="block">
| |
| \Delta p={\frac{0.1\left(0.6821-0.6792\right)}{0.6792}}=0.05
| |
| </math>
| |
|
| |
| <math display="block">
| |
| p_{t+1}=0.1+0.05=0.15
| |
| </math>
| |
|
| |
| C等位因边际适应度高于平均适应度而趋于固定,此条件将持续至C等位在种群中完全固定。
| |
|
| |
| == 习题框7.2答案 ==
| |
|
| |
| 在选择事件#1和#2中,进入分支取代了延续分支。在选择事件#3处,进入分支与延续分支具有相同状态。结果是所有谱系在当前时间均表现为A状态。此情形下,由于选择事件#1的结果,谱系高度更短。见图7.17。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/e999ba119dedb2bcab6ac517a98a523d3bdb356331be4a2abb67d7806fc666d4.jpg]]<br />
| |
| '''图7.17''' 祖先选择图示例:最近共祖(MRCA)具有单倍型状态a,而A为适应性更强的单倍型。当延续分支与进入分支合并时,A单倍型取代a单倍型。
| |
|
| |
| = 第8章 =
| |
|
| |
| === 分子进化 ===
| |
|
| |
| <span id="中性理论"></span>
| |
| ==== 8.1 中性理论 ====
| |
|
| |
| 中性理论及其对多态性水平与分化速率的预测。近中性理论。选择主义与中性主义的争论。
| |
|
| |
| 分子演化领域涉及对DNA、RNA和蛋白质序列的研究,其目标是阐明随时间推移导致序列发生改变和保持恒定的过程。分子演化的一种方法是聚焦于特定基因,试图检验关于该序列的哪些部分最可能参与某种功能或转录调控的假设。分子演化中的另一类研究涉及利用DNA序列数据检验关于过去作用于序列的群体遗传过程的假设。后一类研究常试图区分DNA序列样本中的变异模式是否符合遗传漂变或某些形式的自然选择。分子演化研究中所有假设检验的共同特征是对序列变化的模式和速率使用零假设和备择假设。本章将介绍分子演化中最常用的零假设和备择假设背后的概念基础。尽管本章仅关注DNA序列,但所提出的概念有时也适用于蛋白质序列。
| |
|
| |
| 中性理论目前构成了分子演化中最广泛使用的零模型基础。中性理论认为大多数突变几乎没有或完全没有适应度优势或劣势,因此在选择上是中性的。遗传漂变因此是决定新产生突变命运(固定或丢失)的主要演化过程。中性理论最初提出时,与当时的正统群体遗传理论有重大分歧。在1950和1960年代,人们普遍认为大多数突变具有显著的适应度差异,因此大多数突变的命运由自然选择决定。木村资生(图8.1所示)则认为突变与遗传漂变的相互作用可以解释生物群体中观察到的遗传变异模式以及蛋白质和DNA序列的演化(Kimura 1968,综述见Kimura 1983)。King和Jukes(1969)也在同期提出了类似观点。(关于中性理论的争论以及木村提出中性理论的部分逻辑将在本章本节末尾讨论。)中性理论的零模型在假设仅由遗传漂变决定新突变命运时作出两个主要预测:一是关于单物种群体内取样序列的多态性水平;二是关于不同物种间取样序列的分化程度和速率。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/5f9fe59c3bf3d888674bd57a987123a20c0d19a7fa0d8a31f5d60f45595ba040.jpg]]
| |
|
| |
| Figure 8.1 Motoo Kimura (left) 和 James Crow (right) 于1986年在威斯康星大学麦迪逊分校授予木村资生荣誉博士学位时的合影。木村开创性地使用扩散方程来确定中性突变的平均固定时间或丢失时间等参数。基于这些基础,他于1968年提出了分子演化的中性理论。木村和克劳合作推导了中性遗传变异的基本预期理论框架。克劳指导并合作培养了包括木村在内的许多对群体遗传学有重要贡献的学者。来源:James F. Crow。
| |
|
| |
| 遗传漂变。要理解这种随机游走如何导致多态性,可在任意时间点用直尺形成一条垂直线。若垂直线与任何等位基因频率线相交,则表明此时群体中存在遗传多态性,因为存在多个等位基因在群体中分离。群体中分离的等位基因越多,多态性程度越高。分离的等位基因(即多态性)源于遗传漂变作用下每个突变等位基因频率的随机游走。大多数突变仅在短时间内分离后即从群体中消失。然而,由于它们的频率由随机抽样决定,某些等位基因可能在最终消失前达到较高频率。极小比例的突变在经历等位基因频率的随机游走后最终会在群体中固定。根据中性理论,多态性来源于等位基因在达到固定或丢失终点前的频率瞬态动态过程。图8.2的底层过程可通过Interact Box 5.1近似模拟。
| |
|
| |
| 遗传分化:两个完全隔离谱系间积累的固定遗传差异,这些谱系在从共同祖先分离时原本遗传一致。
| |
|
| |
| 多态性:群体中单个基因座上存在两个或多个等位基因。具有遗传多态性的群体其杂合性、基因多样性或核苷酸多样性度量值均大于0。
| |
|
| |
| 中性理论对群体多态性水平的预测直接源自遗传漂变下等位基因频率动态的预期(见第3章和第5章)。第3章指出,等位基因的初始频率即为其最终固定的概率。对于以单拷贝形式出现于2N个等位基因拷贝群体中的新突变,其最终固定概率为<math display="inline">\textstyle{\frac{1}{2N}}</math>,而最终丢失概率为<math display="inline">\textstyle1-{\frac{1}{2N}}</math>。第3章中遗传漂变的扩散近似还表明:当<math display="inline">N</math>趋大时,新突变的平均固定时间趋近4N代,而平均丢失时间趋近$2({})<math display="inline">2N代(将</math>
| |
|
| |
| <math display="inline">代入式3.40,并令</math>N$趋近无穷大即可验证)。平均固定时间具有较大方差,因此固定代数的标准差预期约为均值的一半,即<math display="inline">2.15N_{e}</math>代(Kimura和Ohta <math display="inline">19696</math>;Narain 1970;Kimura 1970, 1983)。
| |
|
| |
| ==== 多态性 ====
| |
|
| |
| 决定中性理论中多态性的遗传漂变与突变之间的平衡如图8.2所示。每条线表示一个等位基因随时间变化的频率。新突变通过遗传漂变引起的随机游走进入种群(底部边缘的线),并在固定和丢失之间随机波动。
| |
|
| |
| 例如,在<math display="inline">N=1000</math>的种群中,平均丢失时间约为15代(假设<math display="inline">N_e=1</math>),但最终会固定的等位基因的平均固定时间为4000代。此外,由于遗传漂变是随机过程或随机游走,固定时间具有高度变异性。固定时间的标准差很大,约为2150代,这与广泛的固定时间范围一致。预计相对较少的突变会被固定,但那些最终被固定的突变平均而言比大量丢失的突变保持分离状态的时间要长得多。在突变最终走向固定或丢失之前,它们在种群中保持分离状态时会产生多态性。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/b0c8feee36fd8f2185214dc978adb9d07679da8b35b2b1eaa4e29c5d420c9efa.jpg]]<br />
| |
| 图8.2 种群中选择中性突变的命运。新突变以速率<math display="inline">\upmu</math>和初始频率<math display="inline">\textstyle{\frac{1}{2N}}</math>进入种群。等位基因频率是由遗传漂变决定的随机游走。新突变在种群中分离的时间(即突变的分离时间)取决于有效种群大小。然而,新突变走向固定的概率(等于其初始频率)也与有效种群大小直接相关。有效种群大小的这两种效应在等位基因中性时会相互抵消。中性理论预测固定速率为<math display="inline">\upmu</math>,因此预期固定间隔时间为<math display="inline">1/\upmu</math>代。对于最终会固定的突变子集,从引入到固定的预期时间为<math display="inline">4N_{e}</math>代。来源:改编自Kimura (1983)的图3.1。
| |
|
| |
| 理解中性等位基因在种群中预期多态性的另一种方法是考察遗传漂变导致等位基因固定与突变引入新等位基因之间的平衡。第5章显示,在无限等位突变模型中,突变与遗传漂变的联合过程会产生平衡杂合度:
| |
|
| |
| <math display="block">
| |
| H_{平衡}=\frac{4N_{e}\upmu}{4N_{e}\upmu+1}
| |
| </math>
| |
|
| |
| 这取决于有效种群大小<math display="inline">N_{e}</math>和突变率<math display="inline">\upmu</math>(见公式5.39)。在关于中性突变的这种视角下,多态性可能源自以下情形:即使漂变作用强时的高突变输入率、因有效种群大而每个突变的驻留时间长(即使突变率低)、或突变与遗传漂变的中间水平组合。
| |
|
| |
| 中性理论对多态性的预测可以很容易地与正向(基因型适合度高于平均水平)和负向(基因型适合度低于平均水平)自然选择下的预期多态性进行比较(图8.3)。有害的新突变会比中性突变更快消失,因为自然选择会确定性(deterministically)地降低其频率,且等位基因频率几乎不会有随机游走(random walk)。相反,有利的新突变会在自然选择作用下确定性(deterministically)地增加频率直至固定,过程中同样不会有频率的随机游走。受方向性自然选择(directional natural selection)影响的新突变位点,其多态性应低于中性突变位点。另一种可能性是某些有利突变受到由适合度超显性(overdominance)引起的平衡选择(balancing selection)影响。在这种情况下,两个或多个等位基因将具有极长的分离时间,因为自然选择会维持多个等位基因在固定与丢失之间的中间频率,从而导致种群中多态性水平的提升。
| |
|
| |
| 以一个奇妙的隐喻作比:将方向选择、中性演化和平衡选择下的平均固定时间,比作群体遗传学学生从实验室(初始突变)到咖啡店再返回(固定)在不同职业阶段(不同过程)所需的时间。一个刚入学且过度劳累的学生会直奔咖啡店并立即返回,途中不停留与人交谈,因此行程短而直接,如同方向选择。随着经验积累,学生有更多空闲时间,会像随机游走(random walk)般频繁驻足与朋友打招呼。临近毕业时,学生会绕远路去咖啡店,并频繁停留交谈,使得咖啡休息时间极长,如同平衡选择。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/8927d7aad74dc57fca0650ce05531253e1dcc340c40eeb1375b2b29bb2308d78.jpg]]<br />
| |
| 图8.3 若固定和丢失由遗传漂变或自然选择导致,新突变的驻留时间将不同。对于中性突变(B),大多数突变会快速丢失,少数最终固定。无论中性突变最终固定或丢失,其路径均为随机游走(random walk),意味着固定或丢失时间具有高方差。对于因有利而固定的突变(A),方向选择使其在种群中快速固定。因此,在方向选择下,等位基因的分离时间更短,多态性水平低于中性状态。对于显示适合度超显性(overdominance)的突变,自然选择偏好杂合子基因型会无限期维持多个等位基因。因此相较于中性状态,平衡选择显著延长等位基因的分离时间并增加多态性。两种自然选择情形(A和C)均显示负向选择作用于大多数新突变。若新突变有害,则丢失时间极短,且由于选择近乎确定性(deterministic),等位基因频率几乎不会发生随机游走。
| |
|
| |
| <span id="分歧divergence"></span>
| |
| ==== 分歧(Divergence) ====
| |
|
| |
| 中性理论还预测了序列间的'''分歧速率'''(divergence rate)。遗传分歧通过随时间积累的'''替代'''(substitutions)在两条DNA序列中发生。假设两条DNA序列是同一祖先序列的拷贝(图8.4)。在未发生任何替代前,两条序列最初是相同的。随着时间的推移,每个种群中会发生突变,其中一些会因遗传漂变(genetic drift)随机固定(见图8.2)。每个固定的突变会改变序列中随机核苷酸位点的碱基对,导致每条序列逐渐与其祖先序列及姊妹序列产生分歧。一个生物学例子是两个近期从无遗传变异的祖先物种分化出的新物种。这两个新物种将以完全相同的DNA序列为基础形成,此后彼此生殖隔离。比较这两个物种的DNA序列会发现,随时间推移发生的突变导致了各自的DNA序列分歧。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/cf5181f93f9a1d06b796c43a6e08e1fbc4b0345fd29b3cf7f56dadcb07bfcd7f.jpg]]<br />
| |
| '''图8.4''' 两条作为祖先序列相同拷贝的DNA序列的分歧过程。每条序列经历中性突变,其中一些最终通过遗传漂变固定。这些固定突变取代了所有其他等位基因,因此称为'''替代'''(以小写字母表示)。随着替代的积累,两条序列逐渐与祖先序列及彼此产生分歧。在此例中,由于替代,两条序列最终在12个核苷酸位点中有5个位点存在差异。虚线表示携带衍生序列的两个种群完全隔离。
| |
|
| |
| 等位基因的固定概率仅为其初始频率(见第3章)。每一代中,一个等位基因拷贝发生突变的概率为<math display="inline">\mu</math>,总共有<math display="inline">2N</math>个等位基因拷贝。因此,种群中每代新突变的预期数量为<math display="inline">2N\mu</math>。将固定概率乘以每代的突变预期数量:
| |
|
| |
| <math display="block">
| |
| k=\left(2N\mu\right)\frac{1}{2N}
| |
| </math>
| |
|
| |
| 得到以突变形式进入种群的等位基因每代的固定速率,用'''替代速率'''(substitution rate)<math display="inline">k</math>表示。注意该方程可简化为:
| |
|
| |
| <math display="block">
| |
| k=\mu
| |
| </math>
| |
|
| |
| '''替代'''(Substitution): 种群中原本最常见的等位基因被另一个通过突变产生的等位基因完全取代的过程。
| |
|
| |
| 关键假设是:观察替代过程的时间尺度需远长于单个突变平均固定所需时间。若经过超过<math display="inline">4N_{e}</math>代,则种群中所有等位基因很可能因遗传漂变而源自单一等位基因。被固定的幸运等位基因为新突变的概率为<math display="inline">\mu</math>。
| |
|
| |
| 中性理论预测了等位基因替换发生的速率,从而也预测了分歧发生的速率。预测中性等位基因的替换速率需要知道一个等位基因在种群中固定的概率以及每一代发生的新突变数量。在二倍体个体的种群中,一个新突变最初仅以单拷贝的形式存在于该位点的2N个拷贝中。因此,一个新突变的初始频率为<math display="inline">\textstyle{\frac{1}{2N}}</math>。在遗传漂变作用下,任何中性
| |
|
| |
| 这一结果引人注目,因为它指出中性突变每一代被固定的概率(即替换速率)恰好等于突变速率。值得注意的是,预测的替换速率并不依赖于有效种群大小。这是因为较小种群中的突变具有更高的固定机会,但每代产生的新突变数量较少;而较大种群中的突变固定机会较低,但每代产生的新突变数量更多。种群中新突变的输入速率与遗传漂变导致的固定概率在<math display="inline">N</math>变化时精确抵消。需注意,该结果同样适用于单倍体位点,因为此时总共有<math display="inline">N</math>个等位基因,且新突变的固定概率为<math display="inline">\textstyle{\frac{1}{N}}</math>。
| |
|
| |
| 基于替换速率,中性理论还预测最终导致分歧的替换应以恒定的平均速率发生。对于等待时间过程,事件之间的间隔时间是事件速率的倒数。以每天整点报时的时钟为例,报时速率为24次/天,因此报时事件之间的期望间隔时间为1/24天(即1小时)。由于中性替换速率为<math display="inline">\upmu</math>,中性替换之间的期望时间为<math display="inline">1/\upmu</math>代(见图8.2)。例如,若某位点的突变速率为<math display="inline">1\times{10}^{-6}</math>(即每代每<math display="inline">10^{6}</math>个配子发生一次核苷酸变化),则中性替换之间的期望时间平均为<math display="inline">10^{6}</math>代。这为不同位点具有不同分歧速率提供了一种解释:不同位点具有不同的突变速率,从而导致可变的中性替换速率。
| |
|
| |
| ==== 近中性理论 ====
| |
|
| |
| 近中性理论考虑了新突变的命运,前提是部分新突变会受到不同强度的自然选择作用(Ohta和Kimura 1971,Ohta 1972,综述见Ohta 1992和Gillespie 1995)。该理论将新突变分为三类:中性突变、受到正向或负向自然选择强烈作用的突变,以及受到自然选择作用较弱(相对于遗传漂变强度)的突变。最后一类包含近中性突变,因为其命运既不完全由自然选择决定,也不完全由遗传漂变决定。
| |
|
| |
| 对于一个经历自然选择的有限群体中的新突变,方向选择与遗传漂变的力量相互对抗。回顾第3章,遗传漂变导致杂合度以每世代<math display="inline">\frac{1}{2N_{e}}</math>的速率下降。因此,<math display="inline">\frac{1}{2N_{e}}</math>量化了遗传漂变对突变走向固定的“推力”。基因型上的选择系数(s)描述了自然选择对等位基因走向固定或丢失的“推力”。新突变的选择力量可以通过第5章的结果进行量化:固定概率近似为2s(见5.2节的孟德尔式分离模型)。令这两股力量相等:
| |
|
| |
| <math display="block">
| |
| 2s=\frac{1}{2N_{e}}
| |
| </math>
| |
|
| |
| 即得到遗传漂变与自然选择对等位基因频率命运具有近似相等影响力的条件。当<math display="inline">2s</math>处于有效群体大小倒数的一个数量级范围内时,等位基因可被描述为净中性或近中性,因为自然选择和遗传漂变在决定等位基因固定概率上是近似相等的力量。进一步将式8.4两边乘以<math display="inline">2N_{e}</math>可得<math display="inline">4N_{e}s=1</math>,即遗传漂变与自然选择过程相等的条件。当<math display="inline">4N_{e}s</math>远大于1时,自然选择是主导过程;而当<math display="inline">4N_{e}s</math>远小于1时,遗传漂变是主导过程。
| |
|
| |
| 使用更复杂的数学方法,Kimura(1962)证明有限群体中新突变的固定概率为:
| |
|
| |
| <math display="block">
| |
| P_{f i x a t i o n}=\frac{1-e^{-4N_{e}s p}}{1-e^{-4N_{e}s}}
| |
| </math>
| |
|
| |
| 其中<math display="inline">p</math>为等位基因频率(对于单个突变<math display="inline">p=\frac{1}{2N_{e}}</math>,但通常假设<math display="inline">p</math>远小于1),<math display="inline">N_{e}</math>为有效群体大小,<math display="inline">s</math>为假设共显性时的选择系数。该方程与中性理论预期的新突变恒定固定概率共同绘制于图8.5。
| |
|
| |
| 近中性理论预测,替代速率将取决于群体中近中性突变(<math display="inline">\mathrm{4}N_{e}s\approx</math> 1)比例的有效群体大小。因此,近中性理论预测某些突变的群体多态性水平将依赖于有效群体大小。其推论是:因有效群体大小不同,亚群体和不同物种可呈现不同水平的多态性;同理,物种间因<math display="inline">N_{e}</math>差异也可导致分歧率差异。这与中性理论形成对比——后者预测替代速率与有效群体大小无关。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/9c0425b41f7b95868c8ad90081a2e50549ba7f71ad146f887fd86fbda375576d.jpg]]
| |
|
| |
| '''图8.5''' 中性理论与近中性理论下新突变最终固定的概率。根据近中性理论,固定概率取决于自然选择与遗传漂变之间的平衡,表现为有效种群大小与选择系数的乘积(<math display="inline">N_{e}S</math>)。当负选择作用于有害等位基因时,选择系数与<math display="inline">N_{e}S</math>均为负值。<math display="inline">N_{e}S</math>接近零时,固定概率与中性理论的预测值相近。仅当<math display="inline">N_{e}S</math>的绝对值较大时,自然选择才完全主导固定概率。中性理论假设中性突变不受选择影响,其固定概率由有效种群大小决定且恒定。本例中,初始等位基因频率为0.001,即一个二倍体位点的新突变在500个体种群中的频率。来源:仿Ohta(1992)。
| |
|
| |
| <span id="互动框8.1-比较中性理论与近中性理论"></span>
| |
| = 互动框8.1 比较中性理论与近中性理论 =
| |
|
| |
| 使用文本模拟网站比较中性理论与近中性理论的预测。在“模拟”菜单中选择“中性理论模型”。
| |
|
| |
| 以默认参数运行模型。观察左侧“严格中性”与“近中性”下的大图以理解其展示内容。同时查看右侧的直方图,了解每幅图显示的是固定等位基因的固定时间分布与丢失等位基因的丢失时间分布。近中性模型还展示了固定等位基因与丢失等位基因的相对适合度系数分布。
| |
|
| |
| 以一系列递增的<math display="inline">N_{e}</math>值运行模拟。在每次运行中计算<math display="inline">N_{e}S</math>的值。当<math display="inline">N_{e}S</math>变化时,近中性模型的结果如何改变?
| |
|
| |
| ==== 选择论与中性论的争论 ====
| |
|
| |
| 分子演化的中性理论由木村资生于1968年提出(综述见Kimura 1983, 1989),该理论将遗传漂变模型与当时新颖(且稀缺)的氨基酸分歧速率数据相结合。木村利用哺乳动物的氨基酸分歧数据估算出基因组范围内核苷酸替换速率为约每两年一个位点。若自然选择是主导新突变最终替换的主要过程,这将意味着极高的遗传负荷(见第7章)。木村指出,若新突变为中性(满足<math display="inline">|2N_{e}s|</math> <math display="inline"><<1</math>的条件),则遗传负荷将降至合理水平。(在计算负荷的过程中,他还证明中性突变的替换速率近似等于突变速率。)同一论文中,木村基于Hubby与Lewontin(1966)的同工酶多态性数据,估算出在果蝇(''Drosophila'')中观察到的杂合度水平对应中性演化下的有效种群大小介于2300至9000之间。
| |
|
| |
| 中性理论的提出开启了群体遗传学的新纪元,催生了大量旨在解释多态性水平或分歧速率模型的构建(Nei 2005综述)。与此同时,可用于检验群体遗传模型的遗传数据量不断增加。新数据常揭示与中性理论不完全兼容的多态性或分歧模式,推动了中性理论的持续扩展。另一方面,关于自然选择在分子水平作用(如搭车效应、密码子偏好和背景选择)的预测也取得诸多进展,这些成为中性理论的替代假说。在木村(Kimura 1968)首次提出中性理论后,遗传负荷的重要性逐渐减弱,而多态性水平和分歧速率成为主要关注焦点。
| |
|
| |
| 泛中性主义(pan-neutralism)和泛选择主义(pan-selectionism)是选择主义-中性主义争论中某些极端立场的夸张写照。图8.6展示了突变适合度谱的两种版本,分别示意性呈现这两种极端立场(可与图5.1对比)。这两种观点都过于极端,因为它们依赖的突变适合度图景与大多数观测结果不符。中性理论常被误解为主张所有核苷酸或氨基酸变化都是选择中性的(图8.6A)。泛中性主义无法解释诸如基因内同义位点与非同义位点分歧速率差异等分子进化模式(二者具有相同的突变率和有效群体大小)。自然选择导致的功能约束(由King和Jukes 1969首次提出)可以很好地解释这类现象。同时,中性理论也有助于阐明经典假说与平衡假说观点的隐含意义。这两种假说都强调自然选择,倾向于泛选择主义。如图8.6B所示,主张完全不存在中性突变的立场是站不住脚的,因为这需要在选择系数为零处存在适合度谱的不连续性。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/a6658864a9f6c6d1c34ad86ea354d45373f57e6ace9ed02149c9195d89b70d3f.jpg]]<br />
| |
| 图8.6 突变适合度谱的夸张示意图,用以呈现泛选择主义与泛中性主义的极端观点。在泛中性主义视角下(A),几乎所有突变对适合度影响甚微或毫无影响,因此是选择中性的。在泛选择主义视角下(B),几乎没有选择中性的突变,存在大量被负选择的突变以及相对高频率的有利突变。除个别案例外,这两种极端观点均未被大多数观测结果支持。本图灵感源自Turner(1992)和Crow(1972)的插图。
| |
|
| |
| 选择主义与中性主义的争论中,涉及种群中'''同工酶多态性'''水平(通过杂合度或基因多样性估计)的部分至关重要。木村资生(Kimura)和克劳(Crow)(1964)曾在无限等位基因模型下推导出'''漂变-突变平衡'''时杂合度水平的理论预期(见第5章)。中性理论提出后,这一预期被应用于日益增长的蛋白质多态性数据。若中性理论正确,观测到的多态性应与该预测相符。当时的问题是观测到的杂合度范围过于狭窄(见Lewontin 1974)。根据突变率估计,若突变呈中性,所采样的物种在'''有效种群大小'''上应存在显著差异。因此,当时认为观测到的多态性水平过低,与中性理论预测不符。但与此同时,又认为多态性水平过高,无法与经典假说相容。后来的研究表明,关键种群参数(如突变率、假设的有效种群大小)的估计值以及多态性估计值有时存在较大误差,足以导致与理论预期的显著偏离。此外,由于基因、种群和物种的采样有限,经验数据缺乏普适性。正是在这一时期,Lewontin(1974)指出中性理论的预期依赖于一个大的未知数(有效种群大小)与一个小的未知数(突变率)的乘积——这一评论被他反复提及。
| |
|
| |
| 作为中性理论的替代或扩展,大量基于自然选择的多态性解释被提出。其中一项创新假说认为,'''正选择位点周围的遗传搭车'''(genetic hitch-hiking)可能导致多态性水平低于中性理论预期(Maynard Smith和Haigh 1974)。该假说预测,与正选择位点存在'''配子不平衡'''的中性位点会出现多态性降低,这为解释多态性减少提供了可能机制。十年后,Kreitman(1983)关于黑腹果蝇(''Drosophila melanogaster'')'''乙醇脱氢酶'''(alcohol dehydrogenase,''Adh'')基因座的DNA序列数据集为平衡选择假说注入了新活力。''Adh''基因座最初通过同工酶技术研究时已表现出高水平多态性。DNA序列分析揭示了同工酶多态性的分子基础——苏氨酸/赖氨酸差异【“threnine”应译为“苏氨酸”】,并在这些非同义序列变化周围观察到同义变异。总体而言,''Adh''序列的多态性水平过高,不符合严格中性模型,但与平衡选择模型一致。这些数据推动了平衡假说的复兴,并引发了关于DNA水平多态性调控过程的持续争论。
| |
|
| |
| 选择论者与中性论者争论的另一个部分围绕着分歧速率展开。中性理论预测,由于中性替换的预期时间是突变率的倒数,分歧速率应该在时间维度上保持恒定。1970年代收集的氨基酸序列数据和1980年代收集的DNA序列数据表明,替换次数的方差过大,无法与中性理论相容。对这种方差的一个解释是:新突变的固定速率主要受自然选择影响。由于不同突变的自然选择强度存在差异,且会随时间和空间发生变化,自然选择将导致替换速率的变异。特别是自然选择可能导致某些时期几乎没有替换发生,因为有害突变会被选择淘汰,而有利突变则会快速固定。这种高变异的替换速率现象被称为过度分散的分子钟(overdispersed molecular clock),它推动了对简单中性模型的诸多扩展研究,试图解释替换速率的变异程度(参见Gillespie 1991;Culter 2000a)。
| |
|
| |
| 最初,中性理论将突变划分为两个离散类别:中性突变,以及因有害或有利而受自然选择作用的突变。木村资生提出大多数突变属于中性类别。太田朋子为解释与严格中性理论不符的现象(综述见Ohta 1992;Ohta和Gillespie 1996),提出了第三类突变——弱有害突变,即近中性突变。严格中性突变指其选择系数为零,其命运完全由遗传漂变决定。相比之下,近中性突变的命运取决于其所在的有效种群大小背景。当选择系数相对于有效种群大小较小时,突变的命运由遗传漂变决定;反之,当选择系数相对于有效种群大小较大时,同一突变将受到自然选择的作用。
| |
|
| |
| 密码子偏好现象(即观察到的同义密码子使用频率不符合随机预测)是同时需要中性过程和自然选择来解释观测模式的典型案例(综述见Plotkin和Kudla 2011)。自然选择有助于解释为何非同义位点的替换速率低于同义位点——因为非同义位点的改变中有更高比例是有害的,因此自然选择阻止其固定。还有证据表明密码子使用会因基因功能(如翻译速度)而异(例如LaBella et al. 2019)。近中性理论解释了为什么在有效种群规模较大的物种中,密码子使用的选择压力更强。同时,同义位点的固定频率也由突变偏好和遗传漂变共同决定。
| |
|
| |
| 选择主义-中性主义辩论为多态性和分化提出了丰富的预期,涵盖了群体遗传学过程的全部范围,并能解释许多观察到的现象。大多数当代群体遗传学模型的共同特征是,自然选择的强度被表达为相对于遗传漂变强度的比值,后者通过有效群体大小(<math display="inline">N_e</math>)来衡量。如今,自然选择和遗传漂变被视为不可分割的关联过程,它们处于纯选择(大<math display="inline">N_{e}s</math>)与纯漂变(小<math display="inline">N_{e}s</math>)两个极端之间的连续统上。尽管关于自然选择与遗传漂变在产生多态性模式或分化速率中的相对作用仍存在争论,但遗传漂变在预测中始终扮演核心角色。中性理论现已普遍被用作群体遗传学及其各种实证应用的零假设。
| |
|
| |
| <span id="自然选择-1"></span>
| |
| ==== 8.2 自然选择 ====
| |
|
| |
| 正选择、负选择与平衡选择【“Disequilibrium”译为“连锁不平衡”】。连锁不平衡会降低两个位点上自然选择的效率。<br />
| |
| 遗传搭车(Genetic hitch-hiking)与选择性清除(selective sweeps)。背景选择(Background selection)。搭车效应与分化速率。
| |
|
| |
| 自然选择是塑造DNA、RNA和蛋白质序列中观察到的变异的基本过程。分子进化中使用的自然选择模型遵循第6章和第7章描述的内容,并根据自然选择作用于等位基因(尤其是新突变)的不同方式命名。通常采用单倍体适合度模型的自然选择预测,但需注意二倍体适合度模型也被使用(需牢记通常只有二倍体基因型具有适合度,而非单个等位基因)。当考虑DNA序列时,等位基因通常被定义为单个核苷酸位点上可能存在的不同碱基对,当群体中一个核苷酸位点存在两个或多个核苷酸时,称为单核苷酸多态性(SNPs)。
| |
|
| |
| 根据作用于核苷酸位点的定向自然选择的两种一般类型,可识别出新突变具有高于或低于群体平均适合度的适合度值。具有高于平均相对适合度的单倍型经历正向选择,其频率增加并最终达到固定。相反,当单倍型的相对适合度低于平均适合度时,会发生净化选择或负选择,其频率持续下降直至从群体中消失。正向选择和净化选择都预期会导致受选择位点上的多态性相对较少,因为高适合度等位基因在接近固定或丢失的平衡状态时,其频率变化是确定性的(而非随机的)。
| |
|
| |
| 平衡选择也可能存在,其由负频率依赖性选择(见第7章)、杂合基因型更高的相对适合度(见第6章),或随空间或时间变化的相对适合度值所引起。平衡选择的作用将维持群体中两个(或更多)等位基因处于中间频率,极大延长贡献于高适合度杂合基因型的单倍型达到固定或丢失的时间。因此,经历平衡选择的位点预期会维持多态性。与所有形式的自然选择一样,选择强度相对于有效群体大小,如本章前节所述。
| |
|
| |
| '''净化选择或负选择''':在具有低于平均相对适合度的基因型中发现的等位基因频率确定性下降并最终丢失的过程。<br />
| |
| '''正向选择''':在具有高于平均相对适合度的基因型中发现的等位基因频率确定性上升并最终固定的过程。<br />
| |
| '''平衡选择''':通过杂合子优势(或与频率负相关的相对适合度值)维持单一位点上两个或多个等位基因处于中间频率的选择机制。
| |
|
| |
| 在群体遗传学中,通常将位点或核苷酸位点视为独立实体,但进化过程可能既依赖于也影响邻近位点或核苷酸位点。作用于某一位点新有益突变的自然选择可能依赖于其他位点的有益或有害突变的可能性,这一观点早期已被认识(Fisher 1999,初版于1930年;Muller 1932)。然而,对广泛生物类群的核苷酸多态性模式的观察表明,连锁在分子进化模式中起重要作用(回顾第2章,低重组率是导致群体中位点间配子不平衡的众多原因之一)。为预测当两个位点经历自然选择且位点不独立时群体可能发生的情况,已发展出多种模型。
| |
|
| |
| 这些模型采用无上位效应且由单个位点定义适合度的视角,并假设位点间不平衡是突变、连锁和漂变的共同产物。这与适合度具有多位点基础(可能存在上位效应)的自然选择模型形成对比,后者中位点间不平衡是对自然选择的响应产物(见第7章)。
| |
|
| |
| 配子失衡对新突变的影响在分子演化中尤为重要,因为新突变的命运决定了多态性水平和分化速率。当新突变以单拷贝形式进入群体时,它们最初会经历极高程度的配子失衡。仅存在于单拷贝中的新突变将独特地与同一染色体上偶然出现的其他等位基因产生关联。如果新突变受到自然选择的作用,其经历的配子失衡将对基因组邻近位点产生重大影响。首先,让我们探讨中性核苷酸位点与受自然选择作用的核苷酸位点之间配子失衡导致的多态性变化。
| |
|
| |
| Hill和Robertson(1966,Comeron等2008年综述)对有限群体中有益等位基因固定概率进行了开创性研究。他们考虑了两个位点,重点研究了在有限重组和遗传漂变背景下,一个位点经历正选择的有益等位基因固定概率,同时第二个位点也携带有益等位基因的情况。假设第一个位点具有有益等位基因A,第二个位点具有有益等位基因B。当AB配子因漂变和突变引起的配子失衡而过量存在时,选择可以快速改变等位基因频率。但当aB和Ab配子因漂变和突变引起的配子失衡而过量存在时,与位点间自由重组的情况相比,选择固定A等位基因的可能性更低。通过大量重复模拟,他们发现当有效群体大小与重组率的乘积(<math display="inline">N_c</math>)较小时,AB组合达到固定的频率低于<math display="inline">N_c</math>较大时。这种效应的强度还取决于有益等位基因的初始频率、自然选择强度,且在两个等位基因具有相似相对适合度值时最为显著。这种现象被称为Hill-Robertson效应(Felsenstein 1974)或Hill-Robertson干扰。
| |
|
| |
| Maynard Smith和Haigh(1974)提出”遗传搭车”(genetic hitch-hiking)这一术语,用于描述经历强正选择的位点与邻近位点间配子失衡的后果。在该模型中,当自然选择驱动有益突变在群体中达到高频时,与选择突变存在配子失衡的中性等位基因也会因恰好位于有利突变最初出现的单体型上而达到高频。搭车可导致连锁位点上发现的有害等位基因频率增加并固定。搭车的另一个后果是中性等位基因在群体中多态性的丧失,因为当有利突变通过自然选择接近固定时,只有与有利突变存在失衡的一组中性等位基因会保留在群体中。Kaplan等(1989)将原始搭车模型扩展到重复有益突变和重组率变化的连锁区域。
| |
|
| |
| 要理解配子不平衡对新突变的后果,可考虑当一个有利突变在种群中出现时会发生什么。假设当前种群由无性繁殖的单倍体个体组成,因此不存在重组。图8.7展示了有利突变进入种群后等位基因频率随时间的变化。最初,种群包含五种不同的单倍体序列。这些单倍型各自携带若干中性突变,且每个单倍型的中间频率是遗传漂变的产物。一个有利突变(图中以星号标记)随机发生在其中一个单倍型上。随着时间的推移,携带有利突变的染色体因其更高适合度而频率上升,其他单倍型频率则下降。最终,根据突变的相对适合度,携带有利突变的单倍型将趋近于在种群中固定。由于本例中不存在重组,有利突变仅存在于一个单倍型上。因此,该有利突变与恰好属于该单倍型的两个邻近中性突变处于完全配子不平衡状态。
| |
|
| |
| 遗传搭车(genetic hitch-hiking)导致的多态性减少被称为选择性清除(selective sweep),因为当有利突变及其连锁的中性多态位点被自然选择推向高频时,未与被选择位点处于配子不平衡状态的其他中性多态位点会同时被清除出种群。需要强调的是,选择性清除中观察到的多态性减少是自然选择的间接后果,因为只有有利突变本身具有非零有效值的适合度系数。关于选择性清除对连锁中性位点影响的常见(尽管不完美)类比是:与被选择位点的关联会加速固定和丢失的时间进程,类似于有效种群规模的缩减,从而导致多态性降低。理解选择性清除影响的另一种方式是:正选择作用的位点与其连锁位点因共享相同的溯祖基因谱系而产生关联(关于重组的溯祖模型详见本章最后一节)。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/a9f222e7258335ad23b0a110d89c7f79e7edf979db160f43e1c9198e865b9e53.jpg]]
| |
|
| |
| 图 8.7 自然选择对新突变及连锁位点的影响。设想一个包含五种不同DNA单倍型的群体,每个DNA序列由若干中性突变区分,其频率由左侧直方图表示。初始状态下,由于各DNA序列具有中间频率,群体呈现多态性。在A中,第三个DNA序列发生强有利突变,自然选择迅速提高其频率。由有利突变引发的硬清扫(hard sweep)导致连锁位点的多态性极低,因为只有与有利单倍型处于不平衡状态(disequilibrium)的原始中性突变保留在群体中。在B中,初始群体既存在多态性,又存在多个单倍型携带的某个最初中性但后来变为有利的等位基因。软清扫(soft sweep)使携带有利突变的单倍型达到高频率,同时保留连锁位点的中性多态性。在C中,多个单倍型发生有害突变导致负向选择,这些单倍型从群体中消失。此类背景选择(background selection)将群体多态性限制于未经历有害突变的单倍型所携带的等位基因。
| |
|
| |
| 选择性清除(Selective sweeps)还可根据正选择开始作用于单倍型时的初始条件进行区分。硬清扫是强正选择作用于新突变的结果(图 8.7A)。由于新突变最初与其他位点存在强连锁不平衡(linkage disequilibrium),预期连锁位点的多态性会最小化。强选择将在短时间内导致固定,因此附近位点几乎没有时间积累新的中性突变。由于时间短暂,重组事件极少发生,从而维持广泛的连锁不平衡。在硬清扫中,连锁位点的多态性水平会显著降低,仿佛其有效群体大小(effective population size)远小于严格中性的位点。硬清扫还会降低选择位点周围更广泛区域的多态性,因为快速固定过程几乎未给重组事件留下时间(图 8.8)。
| |
|
| |
| “软扫荡”(soft sweep)一词描述了作用于一个已在种群中存在且作为种群'''遗传变异储备'''(standing genetic variation)以中等频率存在的单倍型的正选择(图8.7B)。假设某一位点的所有等位基因最初处于中性演化,并与相邻位点存在中度'''配子不平衡'''(gametic disequilibrium)。随后,环境变化或有效种群规模的急剧增加使某一变体的平均适合度变为有利。在此适合度变化下,正选择将增加有利等位基因及其连锁位点的频率。但由于有利位点最初存在于多态性更高的位点背景上,这些更可变的单倍型池将随有利等位基因频率上升而同步增加。因此,软扫荡预计会减少被选择位点周围较窄区域的多态性,因为携带有利等位基因的单倍型可能已发生重组事件(图8.8)。在软扫荡中,连锁位点的多态性减少幅度也较温和,仿佛其有效种群规模相较于严格中性位点仅适度降低。一个相关模型是'''多次起源软扫荡'''(multiple origin soft sweep),即相同的有利突变(或位置和适合度极为相似的突变)反复发生(Hermisson和Pennings 2005, 2017)。
| |
|
| |
| 关于连锁位点遗传多态性的另一种预测源于以下事实:有害突变的数量远多于有利突变(见第5章)。这表明有害突变上的负选择应普遍存在,并可能影响其他位点的多态性。实际上,针对有害突变的负选择预计会通过'''背景选择'''(background selection)过程减少多态性(Charlesworth等1993, 1995;Charlesworth 2012综述)。有害突变出现在种群中某些单倍型上,导致这些单倍型的丢失率更高(图8.7C)。负选择使有害等位基因趋于丢失,其关联的中性突变也随之丢失。未经历有害突变的单倍型保留在种群中并贡献多态性。在背景选择模型下,重组仅发生在未携带有害突变的单倍型之间,因为这些单倍型在种群中保持分离的时间更长,导致各位点的多态性相对均匀(图8.8)。这与经历选择性扫荡的位点周围预期的多态性下降形成对比。类似搭车效应,背景选择的影响可视为中性位点的有效种群规模<math display="inline">N_{e}</math>降低,因为与有害突变的连锁加速了丢失进程。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/09ebbcdb6f5c33fe4a25c91d006c29da6c319de2da089d60f8ce0150404af890.jpg]]
| |
|
| |
| 图 8.8 自然选择对经历选择的核苷酸位点(空心框)及其通过重组关联的邻近位点(实心框)多态性的影响。严格中性的参考位点多态性作为对比,其水平取决于有效种群大小和突变率。单个位点的强正向选择导致选择性扫荡,由于选择相对于重组更强,即使较远连锁位点的多态性也会被清除。多个位点的正向选择(或对现存遗传变异的正向选择)导致选择性扫荡,但由于选择相对于重组较弱,连锁位点的变异减少范围更小且更局部化。背景选择预期会导致所有位点的多态性相对均匀地减少,因为选择驱动携带有害突变的单倍型走向丢失,留下其他具有中性多态性的单倍型。平衡选择不仅维持受选择位点的多态性,还会增加连锁位点的多态性,因为这些位点有更长的分离时间来积累中性多态性。
| |
|
| |
| '''背景选择(Background selection)''':由纯化选择驱动强有害突变丢失,以及与有害突变关联的中性等位基因因配子不平衡而丢失共同导致的多态性减少。
| |
|
| |
| '''遗传搭车(Genetic hitch-hiking)''':中性等位基因因与受自然选择影响的等位基因存在关联而导致频率上升或下降的过程。
| |
|
| |
| '''选择性扫荡(Selective sweep)''':由于正向自然选择使有利突变频率上升,导致其周围DNA序列区域多态性减少或消失的现象。多态性减少是重组未能打破有利突变与邻近中性位点间的配子不平衡所致。
| |
|
| |
| 配子不平衡如同无动力的滑翔机,通过”搭乘”正向选择提高的固定概率而实现固定。Gillespie指出遗传漂流(genetic draft)是一个随机过程,因为最终达到固定的中性突变是通过随机与受选择突变关联而实现的。因此,即使有效种群大小无限大,对有利突变的正向选择仍会导致从可用中性突变池中随机抽取有限样本。
| |
|
| |
| 另一种可能性是新突变受到''balancing selection''的作用,最终使同一位点上的新有益突变达到中等频率,并在种群中长期维持。''Balancing selection''也预计会影响与受选位点处于'''gametic disequilibrium'''的中性位点的多态性。当一个新的有益突变出现在受''balancing selection''作用的位点时,其频率的初始增加会产生类似选择性清除(selective sweep)的效应。然而,长期的''balancing selection''会导致多态性增加,因为''balancing selection''维持了在种群中长期存在的多个等位基因(图8.8)。这些被选择的等位基因随后可以在与受选位点处于'''gametic disequilibrium'''的中性位点上积累突变,逐步累积多态性。与独立的中性位点相比,与受''balancing selection''位点处于'''gametic disequilibrium'''的中性位点的分离时间显著延长,从而有更多机会经历导致多态性积累的突变(Charlesworth 2006综述)。
| |
|
| |
| Gillespie(2000)研究了伪搭车模型(pseudo-hitch-hiking model),以预测大种群中反复正向选择产生一系列选择性清除对多态性的影响。在该模型中,连锁位点的多态性高度依赖于重组率、新有益突变的速率及其相对适合度值。Gillespie(2001)将反复选择性清除对连锁核苷酸位点多态性的影响称为'''genetic draft'''【“genetic draft”译为“遗传漂变”】,因为与受选位点连锁的中性突变会通过…
| |
|
| |
| 这些自然选择模式单独或共同作用的影响,取决于一系列可能因基因组区域和物种而异的群体遗传参数。受选择位点与中性位点之间的关联强度将随重组率变化。亲属间交配和自交预计会降低实际重组率,因为纯合位点间的交叉重组无效应(Glémin et al. 2006, Andersen et al. 2012)。选择的频率取决于突变的绝对速率,而选择模式则取决于有利突变与有害突变的相对速率。选择相对于其他过程的强度将随选择系数的分布而变化。对选择的响应还取决于突变的效应大小以及显性度或隐性基因作用程度,通常称为遗传架构(见Chapter 9)。种群分化可能影响这些类型自然选择的作用(Bierne 2010)。例如,当选择性清除促进局部适应时,其信号可能仅限于部分亚种群,且选择的影响可能进一步受亚种群间基因流历史的调控。有效种群大小及其随时间因群体统计变化产生的波动也将影响选择的作用,因为每代预期突变数是有效突变率<math display="inline">(\Theta=4N_{e}\mu)</math>的函数,而有效种群大小将决定选择与遗传漂变的相对强度。
| |
|
| |
| ==== 搭车效应与分化速率 ====
| |
|
| |
| 不同物种间及物种内的遗传分化是各物种内发生替换事件的产物。当新突变的固定概率由自然选择决定时,分化速率将相对于遗传漂变预期速率发生变化。正向自然选择加速分化,因为有利突变平均比仅靠遗传漂变更快固定。反之,负向自然选择减缓分化速率,因为有害突变迅速丢失,且可能固定并产生替换的中性突变更少。此时的问题是:若中性位点与受自然选择作用的核苷酸位点存在连锁不平衡,中性位点的分化速率将加快还是减慢。
| |
|
| |
| 物种内替换的预期速率由标度化突变率<math display="inline">\textstyle(2N_{e}\mu={\frac{\theta}{2}})</math>和突变固定概率<math display="inline">(P_{F})</math>决定,其方程可表述为:
| |
|
| |
| <math display="block">
| |
| k=\frac{\theta}{2}P_{F}
| |
| </math>
| |
|
| |
| 如本章前文所示,对于独立中性突变,<math display="inline">\begin{array}{r}{P_{F}=\frac{1}{2N}}\end{array}</math>,这也是每个新突变的初始频率。此处我们使用新符号表示固定概率,因为当突变与受选位点存在配子不平衡时,中性突变的固定概率<math display="inline">(P_{F})</math>可能与独立突变时不同。
| |
|
| |
| 假设我们有一个中性位点,包含两个等位基因A和a。A等位基因的频率为<math display="inline">x</math>,因此a等位基因的频率为<math display="inline">1-x</math>。进一步假设这个中性位点与另一个受极强正向自然选择作用的选择位点完全连锁。假设在选择位点发生了一个新的无限有利的突变,并立即固定。此时中性位点的A等位基因因搭车效应(hitch-hiking)而同样被固定的概率是多少?
| |
|
| |
| 中性位点的A等位基因频率为<math display="inline">x</math>,因此选择位点的新有利突变与A等位基因连锁的概率也为<math display="inline">x</math>。因此,存在<math display="inline">x</math>的概率使得A等位基因会随着选择位点的新突变一起”扫荡”至固定。然而,仅通过遗传漂变使A等位基因固定的概率同样为<math display="inline">x</math>,因为这是A等位基因的初始频率。由此可见,即使与选择位点完全连锁,也不会改变A等位基因的固定概率。
| |
|
| |
| Birky和Walsh(1988)提出了这一观点,并通过更普适性的解析推导和模拟结果证明:无论正向还是负向自然选择都不会改变中性位点的替代速率。这是因为与选择位点连锁的中性等位基因拷贝替代概率的增加,恰好被所有未与选择位点连锁的中性等位基因拷贝固定概率的等量减少所抵消。
| |
|
| |
| ==== 实证研究 ====
| |
|
| |
| 在系统梳理了多种自然选择模型及其对连锁位点多态性的间接影响,并解释了为何物种间的分化不受选择位点连锁的影响后,我们就能充分理解一系列实证研究的结果——这些研究旨在检测有限重组条件下不同形式的自然选择作用。
| |
|
| |
| 对果蝇(''Drosophila'')群体中多个基因座的遗传变异研究的一个常见结果是,多态性水平与重组率呈正相关(Hudson 1994;Cutter 和 Payseur 2013 综述)。关于多态性与重组率之间关系的成因存在多种假说。一个与严格中性理论相一致的假说认为,基因座的重组率可能与其突变率存在某种关联,使得标度化突变率在重组率较高的区域更大(Hellmann et al. 2003, 2005)。例如,引发重组的分子过程可能同时导致点突变。回想中性理论预测多态性水平与分化率是相关的,因为两者最终都是突变率的产物。由此可推导出:若果蝇基因座中重组与多态性的关系由中性过程解释,则多态性水平和分化率都应与重组率相关(Begun 和 Aquadro 1992)。
| |
|
| |
| 图8.9展示了用于检验果蝇中多态性与重组率相关性的中性假说的数据。虽然黑腹果蝇(''D. melanogaster'')的多态性随重组率增加而显著上升,但黑腹果蝇(''D. melanogaster'')与拟果蝇(''Drosophila simulans'')在部分相同基因座上的分化水平却与重组率无关。这些数据因此否定了严格中性假说。
| |
|
| |
| 另一种解释是自然选择对有利突变的作用导致了选择性清除(selective sweeps)。遗传搭车(genetic hitch-hiking)的强度及因选择性清除而丢失的多态性数量会随着重组率的增加而减少,因为重组减少了受选择突变与邻近位点间的配子不平衡。然而,选择性清除对分化率没有影响,因此分化率不会显示出与重组率的相关性。综上,选择性清除假说与果蝇DNA序列数据中多态性随重组率增加的现象是吻合的。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/ca0f971e40c7384f8f5355f1c9e3e9ed722e2c0eaf8722e2b84658e0d8baef5f.jpg]]
| |
|
| |
| 图 8.9 根据多个基因座的重组率度量指标(交换系数),绘制黑腹果蝇(''Drosophila melanogaster'')种群内核苷酸多样性(A)及其与模拟果蝇(''Drosophila simulans'')间的分化程度(B)的关系图。随着重组率降低,基因座的核苷酸多样性也随之减少(A)。若重组率较低的基因座恰好也具有较低的突变率,则中性理论可解释多态性与重组率的相关性。在此中性假说下,分化速率也应与重组率相关,因为多态性和分化程度均随突变率增加而增加。对重组与多态性相关性的另一种解释是,自然选择对有利突变的作用引发了搭车效应,并因选择性清除导致多态性减少。部分基因座的分化速率(B)表明分化速率与重组率无关,否定了针对这些数据的中性假说。来源:数据来自Begun和Aquadro(1992)。
| |
|
| |
| 当前的一个挑战是区分选择性清除与背景选择(Innan和Stephan 2003;Stephan 2010)。基因组尺度的多态性研究为检验这两类自然选择对多态性影响的假说提供了更多机会。Lohmueller等(2011)的一项被广泛引用的研究发现,人类中重组率较低的区域多态性减少,且基因附近区域低频等位基因较为罕见。为建立适用于人类种群参数的预测模型,他们进行了多组模拟,旨在生成仅由背景选择或背景选择与正向选择共同作用(导致选择性清除)下的预期多态性模式。其模拟结果表明,人类多态性数据中观察到的模式可通过单独的背景选择或背景结合少量选择性清除来解释。然而,单独模拟的选择性清除与数据中观察到的多态性与重组率相关性不符。
| |
|
| |
| 线粒体DNA在动物多态性研究中被广泛用作遗传标记(Avise等1987;Harrison 1989)。学界普遍认为线粒体多态性是中性演化的产物,种群接近漂变-突变平衡,且线粒体多样性与有效种群大小呈正相关。然而,线粒体基因组中重组过程的缺失为选择性清除和背景选择提供了必要条件。这使许多研究者提出假说:自然选择及其对连锁位点的影响应降低线粒体基因组多态性(Dowling等2008;Galtier等2009综述)。
| |
|
| |
| = 对动物线粒体基因组多态性非中性模式的检验 =
| |
|
| |
| 通过比较核同工酶位点、核DNA序列和线粒体DNA序列的多态性测量值,对动物线粒体基因组中多态性的非中性模式进行了检验(三种数据类型分别涵盖912、417和1683个物种,样本具有广泛分类学代表性)。Bazin等人(2006)使用这种比较方法来检验中性假说——由于所有三类位点共享相似的有效种群大小,物种内三类数据的多态性应呈现相关性(由于线粒体基因组是单倍体且单亲遗传,其有效种群大小为双亲遗传的二倍体核位点的四分之一)。
| |
|
| |
| 根据普查种群大小,昆虫、棘皮动物(echinoderms)和软体动物(mollusks)的有效种群大小预计大于哺乳动物、鱼类、爬行动物和鸟类。中性理论预测,具有较大有效种群大小的分类群在相同位点上也应具有更高水平的多态性。核同工酶和DNA序列数据符合中性预测,因为昆虫、棘皮动物和软体动物的多态性高于哺乳动物、鱼类、爬行动物和鸟类。相比之下,线粒体多态性在所有动物类群中均处于低水平且近乎一致,未显示出与核同工酶和DNA序列多态性水平的相关性。这一结果可通过遗传搭车(genetic hitch-hiking)导致非重组线粒体基因组中的选择性清除来解释。
| |
|
| |
| <span id="bazin等人2006研究的局限性"></span>
| |
| == Bazin等人(2006)研究的局限性 ==
| |
|
| |
| 该研究存在若干限制:未对被比较物种的系统发育关联性进行校正(由于部分物种因近期共同祖先而具有相似性,可能导致相关性膨胀;Felsenstein 1985);此外,比较的高度分化物种可能在线粒体基因组突变率等未测量变量(除已测量的普查种群大小外)上存在差异。基于这些限制,Nabholtz等人(2008)开展后续研究:在277个哺乳动物物种(分化时间较近、分类学范围更小)中重复相同检验,并校正种群分化、以替代率作为谱系突变率代理变量以及系统发育关系。
| |
|
| |
| 改进后的研究发现,同工酶杂合度与线粒体核苷酸多样性之间存在符合中性预测的相关性。同时发现线粒体核苷酸多样性存在显著的分类学变异,表明线粒体突变率在物种间差异巨大。作者得出结论:线粒体多态性未显示选择性清除或强背景选择的证据,但仍可能如通常假设的那样仅微弱反映近期有效种群大小。
| |
|
| |
| 关于自然选择的预测及其对关联位点的影响(这些预测并非互斥)共同构成了严格中性零模型的替代假说。这些形式的自然选择有助于解释为何基因组某些区域及某些物种的DNA序列多态性水平可能仅微弱依赖于有效种群大小——这一猜想有时被称为'''Lewontin悖论'''(Lewontin 1974, 1985a)。关于何种进化过程的相对平衡最能解释遗传多态性模式的问题至今仍在探讨中,并随着模型预测的持续完善和实证数据的大幅扩展而更新(如Leffler et al. 2012; Hague and Routman 2016)。
| |
|
| |
| <span id="分歧度与多态性的测度"></span>
| |
| ==== 8.3 分歧度与多态性的测度 ====
| |
|
| |
| '''DNA序列分歧度的测量'''<br />
| |
| 核苷酸替代模型通过校正饱和度对分歧度估计值进行修正。
| |
|
| |
| '''通过分离位点数与核苷酸多样性衡量DNA多态性'''
| |
|
| |
| 大多数自然群体和实验室群体至少存在一定量(通常为大量)由基因组中众多位点的不同等位基因所代表的遗传变异。基因组的最小可比单元是同源核苷酸位点,即个体间完全相同的基因组位置上可比较的单碱基对位点。此类核苷酸位点上的种内遗传变异以存在不同核苷酸的DNA序列为特征(例如在同一基因起始密码子后第37个碱基对处,某些个体为A而其他个体为T),称为'''核苷酸多态性'''。核苷酸多态性有时被称为'''单核苷酸多态性'''或SNPs(发音为”snips”)。不同物种间的遗传变异称为'''分歧度''',它是各物种内部发生的、共同导致DNA序列差异的替代事件的产物。本章本节将介绍基于DNA序列数据估计分歧度与多态性的常用测度方法。
| |
|
| |
| <span id="专栏8.1-dna测序"></span>
| |
| = 专栏8.1 DNA测序 =
| |
|
| |
| DNA测序技术的稳步发展(Heather and Chain 2016)催生了用于观测SNPs和序列分歧度的大量DNA序列数据。DNA测序技术的持续进步预示着更快、更低成本的数据采集。第一代DNA测序技术(即'''Sanger测序''')采用合成测序法,利用DNA聚合酶复制序列模板并随机掺入链终止双脱氧核苷酸(双脱氧核苷酸缺乏维持DNA链沿5′→3′方向延伸所需的3′羟基(-OH)基团)。通过电泳以单碱基对分辨率分离不同长度的序列群体,并使用放射性或荧光标记检测终止每条序列的双脱氧核苷酸状态(图8.10)。Sanger测序可生成最长约750个核苷酸的单条序列。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/2954a9ab34bfbd1bd262fadf1f57153db8a73546b6e79c96be65a5bd7f765b9e.jpg]]
| |
|
| |
| Figure 8.10 通过双脱氧核苷酸终止的Sanger测序法产生的单碱基对片段电泳图谱,其中每个核苷酸具有不同的分子标记。
| |
|
| |
| <span id="box-8.1-续"></span>
| |
| = Box 8.1 (续) =
| |
|
| |
| 主要的第二代测序技术——焦磷酸测序(pyrosequencing)——同样依赖DNA聚合酶复制序列模板。当DNA聚合酶将互补的脱氧核苷酸添加到复制的DNA链时,会释放出焦磷酸(pyrophosphate)。一种酶(ATP硫酸化酶)将释放的焦磷酸转化为ATP,促使化学发光酶释放光信号。当A、T、C或G核苷酸溶液被冲洗过DNA模板且下一个核苷酸被添加到复制链时,探测器会测量发出的光。焦磷酸测序可通过微流控装置并行处理大量独立模板链,目前已有多种基于该通用原理的方法。焦磷酸测序生成的单条序列长度可达约300个核苷酸,显著短于Sanger测序的产物。这些短读长序列的操纵与组装对计算提出了重大挑战。
| |
|
| |
| 第三代(有时称为第四代)测序技术有望实现更长的单条序列读长,并具备更少的模板制备步骤和改进的序列组装潜力。其中一项技术称为单分子实时(SMRT)测序,其原理是将DNA聚合酶固定在名为零模波导(ZMW)的孔洞底部。ZMW的宽度小于激发荧光标记核苷酸所用光的波长,因此仅在孔洞底部——即DNA聚合酶复制模板的位置——产生照明。ZMW孔洞大幅降低了背景荧光,并使所有标记核苷酸始终处于溶液中,无需耗时更换核苷酸溶液。第二种方法是纳米孔测序(Feng et al. 2015),即通过极小孔径对单个核苷酸或单链DNA进行电泳。该孔洞可以是α溶血素(''alpha hemolysin'')等生物蛋白或固态装置。通过测量不同核苷酸穿过孔洞时的电流变化或使用荧光探针,可检测核苷酸状态。
| |
|
| |
| <span id="dna-divergence-between-species"></span>
| |
| ==== DNA divergence between species ====
| |
|
| |
| 量化分子进化最基本的方法是通过比较两条DNA序列。这一比较分为两个步骤。首先,两条DNA序列必须进行比对,使得每条序列的同源核苷酸位点都排列在同一列中。例如,若对两个编码基因进行测序,则一种比对方式是将组成起始密码子的前三个核苷酸进行匹配。(序列比对的方法超出本文范围,读者可参考Page和Holmes(1998)等文献获取更多细节。)第二步是确定具有不同核苷酸的位点数量。两条DNA序列之间不同的核苷酸位点数除以比较的总核苷酸位点数,即得到核苷酸位点差异的比例,通常称为<math display="inline">\pmb{p}</math>-距离(proportion distance的简称)。这是衡量两条DNA序列自共同祖先(当它们还是同一序列的完全相同副本)分化以来所发生进化事件的基本指标。
| |
|
| |
| <math display="inline">p</math>-距离(<math display="inline">p</math>-distance):两条DNA序列之间不同的核苷酸位点数除以总核苷酸位点数,作为比例距离(proportion distance)的简称,有时用<math display="inline">d</math>(distance)表示。
| |
|
| |
| 图8.4展示了一对序列间的分歧示例。考虑经过某些替换事件分化后,在现时点最右侧的两条序列。在总共12个核苷酸位点中,有5个位点具有不同的核苷酸。因此,<math display="inline">p</math>-距离为<math display="inline">5/12=0.3125</math>,即31.25%的核苷酸位点发生了分歧。
| |
|
| |
| 从完全独立的群体中取样的两条DNA序列之间的<math display="inline">p</math>-距离应随时间增加,因为每个群体内的替换会逐渐取代最初因共同祖先而共享的核苷酸。若两条DNA序列代表两个不同物种或完全隔离的群体,则<math display="inline">p</math>-距离可作为这两个物种间分歧程度的度量。
| |
|
| |
| <span id="dna序列分歧与饱和"></span>
| |
| ==== DNA序列分歧与饱和 ====
| |
|
| |
| = 饱和现象 =
| |
|
| |
| '''饱和现象'''(saturation)是指即使分化时间持续增加,DNA序列的差异度(divergence)看似减缓并最终达到平台期的现象。核苷酸随时间推移产生的饱和现象是由同一核苷酸位点发生多次替换引起的,这种现象称为'''多次击中替换'''(multiple hit substitution)(参见第5章关于“多次击中突变”的相关主题)。同一位点重复发生的替换会掩盖过去替换的信息,因为只有最近一次替换可被观测并量化为两条DNA序列间的差异度。计算两条序列的<math display="inline">p</math>-distance(p距离)会导致对已发生替换次数的低估,从而低估差异程度。图8.11的上图显示,分化时间增加时,差异度呈线性增长(虚线)或呈现饱和现象(实线)。实际DNA序列数据通常表现出一定程度的饱和,如图8.11下图所示:对几种牛科物种(包括家牛、野牛、水牛和牦牛等偶蹄目动物)的线粒体细胞色素<math display="inline">c</math>氧化酶亚基II基因测序结果显示,这些物种的分化时间介于200万至2000万年前。
| |
|
| |
| 理解饱和现象可借助随机组装一条DNA序列并与现有序列比较的假想过程。设想从一个含有等量A、C、G、T碱基对的桶中随机抽取核苷酸。若现有序列的某位点为A,随机抽取的核苷酸有25%的概率为A(位点匹配),75%的概率为T、C或G(位点差异)。因此,以等频率随机组装的DNA序列与另一条序列的平均差异度应为75%(或25%的相似度)。其结果是,两条同源序列的差异度不会随时间无限增加。最终,持续突变会使共享位点随机化,最大差异度将稳定在75%的平台期。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/bad3eada44d00698df1b9503fbdf9dee2908ee320e9a78db099c5dbee3a41ee5.jpg]]
| |
|
| |
| 【注:原文中“<math display="inline">p</math>-distance”译为“p距离”,指未校正的序列差异比例。】
| |
|
| |
| 图 8.11 随着从共同祖先分歧的时间增加,同一核苷酸位点反复发生的替换会导致核苷酸变化的饱和。如顶部面板虚线所示,替换速率并未改变且总替换数随时间持续增加(代表真实替换数)。相比之下,同一位点的多重替换导致分歧估计值增长放缓并趋于平稳(顶部面板实线)。因此,分歧程度会使人产生分歧速率随时间下降的认知。底部面板显示了牛科物种(包括家牛、美洲野牛、水牛和牦牛等有蹄类)线粒体细胞色素c氧化酶亚基II基因在200万至2000万年前分歧后的分歧与饱和情况。顶部面板中,<math display="inline">\alpha=1\times{{10}^{-6}}</math>。底部面板数据来自Janecek等人(1996),曲线为二次回归拟合。
| |
|
| |
| 存在多种方法可通过校正观测到的两条DNA序列间的分歧度,在考虑多重命中后获得更接近真实分歧度的估计值。这些校正方法被称为核苷酸替换模型,利用DNA碱基频率和替换速率等参数来修正两条DNA序列间的分歧估计。其中最简单的是以其作者命名的Jukes和Cantor(1969)核苷酸替换模型。通过推导Jukes-Cantor模型,可以深入理解核苷酸替换模型的运作机制。
| |
|
| |
| Jukes-Cantor模型的基本假设是:DNA序列中任一核苷酸被其他三种核苷酸替换的可能性均等。例如,若某位点当前为C,则被A、T或G替换的概率相同。图8.12展示了核苷酸位点可能发生的三种事件:(i)发生且仅发生一次替换;(ii)未发生任何替换;(iii)发生替换后再次发生独立替换使位点恢复原始状态。第一种情况下,感知分歧度与真实分歧度一致,无需校正。第二、三种情况的感知分歧度相同,但实际发生的事件截然不同。第三种情况中,部分看似未分歧的核苷酸位点实际上已发生过替换。Jukes-Cantor等核苷酸替换模型的作用,正是估计这些看似未分歧实则已分歧的核苷酸位点比例。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/2bdc49a3811fcf3c02f26ebfdb1c347bc2dc8de06c2ff72e4a9ac58268d2aa33.jpg]]
| |
|
| |
| 图8.12 单个核苷酸位点在两代间可能经历的三种事件类型。例如,某个核苷酸位点最初可能是G。在情况1中,第一代的单次替换事件将G变为A、C或T核苷酸,该核苷酸在第二代仍保持不变。此时,用''p''-distance测量分歧度能准确计算替换次数。在情况2和3中,该核苷酸位点仍保留初始核苷酸,给人未发生替换的印象。情况2中该印象是准确的,但情况3中存在两次未被简单''p''-distance测量方法计算的替换事件。
| |
|
| |
| <span id="interact框8.2-比较核苷酸替换模型"></span>
| |
| = Interact框8.2 比较核苷酸替换模型 =
| |
|
| |
| 使用文本模拟网站观察不同核苷酸替换模型如何校正估计的DNA分歧度。在模拟菜单中,选择Nuc Substitution模型。该模拟根据用户设定参数,在两条独立DNA序列中生成突变。序列模拟参数可单独设置,或通过右侧按钮根据替换模型参数数量自动设置。
| |
|
| |
| 使用默认参数运行模型。观察图表中显示的时间与''p''-distance(标记为观测分歧度)估计的序列分歧度,以及使用四种不同参数数量的核苷酸替换模型校正后的结果。
| |
|
| |
| 时间与两条序列均经历突变的位点(即实际发生替换的位点真实比例)有何关系?时间与''p''-distance有何关系?
| |
|
| |
| 针对图中四种核苷酸替换模型,绘制以核苷酸为顶点的正方形,并用线型或颜色表示速率参数。同时描述每个模型的平衡碱基频率。不同核苷酸替换模型对表观分歧度的校正效果如何?校正效果如何依赖于DNA替换模拟所用的参数?
| |
|
| |
| 在Jukes–Cantor模型中,核苷酸替换概率通常用<math display="inline">\upalpha</math>(读作“alpha”)表示。由于每个位点的当前核苷酸可能被三种其他核苷酸替换且概率相等,任何替换的总概率为<math display="inline">3\upalpha</math>。因此,若第零代是G,一代后仍为G的概率为
| |
|
| |
| <math display="block">
| |
| P_{G(t=1)}=1-3\alpha
| |
| </math>
| |
|
| |
| 由于各代替换概率独立,两代内未发生替换的概率为
| |
|
| |
| <math display="block">
| |
| P_{G(t=2)}=\left(1-3\alpha\right)^{2}
| |
| </math>
| |
|
| |
| 该式给出了核苷酸在两代间未改变的概率(如图8.12情况2所示)。
| |
|
| |
| 我们还需要确定某个核苷酸发生两次变化的概率,如图8.12案例3所示。从第零世代到第一世代,发生替换的概率是<math display="inline">3\alpha</math>。这个概率也可以表示为1减去未发生替换的概率,即<math display="inline">1-P_{G(t=1)}</math>。从第一世代到第二世代,只有一种碱基的替换能使该位点恢复初始状态。这种情况发生的概率即替换概率<math display="inline">\alpha</math>。将这两个独立概率相乘,就得到多重击中性替换事件发生的概率,这种替换会使核苷酸恢复初始状态:
| |
|
| |
| <math display="block">
| |
| P_{G(t=2)}=\alpha\big(1-P_{G(t=1)}\big)
| |
| </math>
| |
|
| |
| 该式表示两次替换事件发生的概率,这两种替换都无法通过比较第二时间的DNA序列被检测到。
| |
|
| |
| 结合这两个结果,可以得到核苷酸位点在两个世代后仍保持相同碱基对的概率:
| |
|
| |
| <math display="block">
| |
| P_{G(t=2)}=\bigl(1-3\alpha\bigr)P_{G(t=1)}+\alpha\bigl(1-P_{G(t=1)}\bigr)
| |
| </math>
| |
|
| |
| 这个结果与两个世代间发生的替换次数无关。由于替换和未替换的概率在各世代间相互独立,该方程可以推广为更一般的形式:
| |
|
| |
| <math display="block">
| |
| P_{G(t+1)}=\bigl(1-3\alpha\bigr)P_{G(t)}+\alpha\bigl(1-P_{G(t)}\bigr)
| |
| </math>
| |
|
| |
| 或写作适用于相隔一个世代的任意两个时间段的递推方程。该递推方程还可以表示为初始核苷酸位点随时间保持不变的【“change in the probability”译为”概率变化”】。由于量的变化是当前值与前一时刻值的差值,某位点特定核苷酸在一个世代内的概率变化可以表示为:
| |
|
| |
| <math display="block">
| |
| \Delta P_{G(t)}=(1-3\alpha)P_{G(t)}+\alpha\big(1-P_{G(t)}\big)-P_{G(t)}
| |
| </math>
| |
|
| |
| 展开方程右边各项可得:
| |
|
| |
| <math display="block">
| |
| \Delta P_{G(t)}=P_{G(t)}-3\alpha P_{G(t)}+\alpha-\alpha P_{G(t)}-P_{G(t)}
| |
| </math>
| |
|
| |
| 简化为:
| |
|
| |
| <math display="block">
| |
| \Delta P_{G(t)}=\alpha-4\alpha P_{G(t)}
| |
| </math>
| |
|
| |
| 我们目前建立的模型将时间视为离散步长(如图8.12)。若考虑任意时间<math display="inline">t</math>的【“rate of change”译为”变化率”】,则核苷酸位点表型保持相同的概率随时间变化可表示为微分方程<math display="inline">dG/dt = \alpha - 4\alpha P_{G(t)}</math>。该方程的解为:
| |
|
| |
| <math display="block">
| |
| P_{G(t)}=\frac{1}{4}+\left(P_{G(t=0)}-\frac{1}{4}\right)e^{-4\alpha t}
| |
| </math>
| |
|
| |
| 这与具有环境容纳量的种群的指数增长方程类似。当<math display="inline">t</math>趋大时,<math display="inline">e^{-4\alpha t}</math>项趋近于0,此时<math display="inline">P_{G(t)}</math>趋近于<math display="inline">\%</math>。
| |
|
| |
| 使用连续时间方程时,某核苷酸位点随时间保持为G的概率取决于初始状态和替换速率(图8.13)。若某位点初始为G,则<math display="inline">P_{G(t=0)}=1</math>,该位点随时间保持为G的概率为:
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/b407bf6c89f9c7327a6982ffbac2e44936f7b3ebc1cd993badb47235ce020f49.jpg]]
| |
|
| |
| 图 8.13 Jukes-Cantor核苷酸替换模型下某一位点保留其原始碱基对的概率。例如,若某核苷酸位点最初为G,则该位点保持G的概率随时间推移持续下降。若某位点最初非G(即A、C或T),则该位点变为G的概率随时间推移上升。某特定碱基存在的概率最终会收敛于<math display="inline">25\%</math>,因为当替换到各核苷酸的概率相等时,随机采样获得特定碱基的概率即为该值。上图中<math display="inline">\alpha=1\times{10}^{-6}</math>,下图中α = 1 × 10 5。
| |
|
| |
| <math display="block">
| |
| P_{G(t)}=\frac{1}{4}+\frac{3}{4}e^{-4\alpha t}
| |
| </math>
| |
|
| |
| 该概率随<math display="inline">t</math>增加呈指数级趋近于<math display="inline">25\%</math>。相反,若某位点初始非<math display="inline">\mathrm{G}</math>,则<math display="inline">P_{G(t)}=0</math>。该位点随时间保持为G的概率为
| |
|
| |
| <math display="block">
| |
| P_{G(t)}=\frac{1}{4}-\frac{1}{4}e^{-4\alpha t}
| |
| </math>
| |
|
| |
| 该概率随时间推移从0上升至<math display="inline">25\%</math>。注意<math display="inline">25\%</math>即为从随机抽取的等频核苷酸序列中,某位点与已有序列同一位点匹配的概率。此外,由于指数项中的<math display="inline">-4\upalpha t</math>,当替换速率<math display="inline">\upalpha</math>增大时,趋近<math display="inline">25\%</math>的速度会加快。
| |
|
| |
| 我们最初的目的是校正观测到的序列间差异(即<math display="inline">p</math>-距离)中的多重替换事件。现有序列变化模型为校正提供了基础,但仍需进一步推导实际校正方法。考虑两条在时间0时每个位点均同源的DNA序列,在时间<math display="inline">t</math>时,任意位点保持相同核苷酸的概率为
| |
|
| |
| <math display="block">
| |
| P_{I(t)}=\frac{1}{4}+\frac{3}{4}e^{-8\alpha t}
| |
| </math>
| |
|
| |
| 其中<math display="inline">P_{I(t)}</math>表示某位点核苷酸相同的概率。此时指数项为<math display="inline">e^{-8\alpha t}</math>,因为两条DNA序列可独立变化,导致核苷酸保持相同的概率随时间衰减速度加倍。两序列位点差异(或称分歧)的概率<math display="inline">d</math>随时间变化为1减去相同概率,即
| |
|
| |
| <math display="block">
| |
| d=\frac{3}{4}\left(1-e^{-8\alpha t}\right)
| |
| </math>
| |
|
| |
| 通过对等式右侧取自然对数并整理,可解出指数项:
| |
|
| |
| <math display="block">
| |
| 8\alpha t=-\ln{\left(1-\frac{4d}{3}\right)}
| |
| </math>
| |
|
| |
| 该式表明:替换速率八倍于时间之积与两条DNA序列间的预期分歧量相关。对于初始同源的两条DNA序列,每个位点的预期替换概率为<math display="inline">3αt</math>。由于存在两条序列,某位点产生分歧的概率为<math display="inline">6\upalpha t</math>。设预期分歧度<math display="inline">K=6\upalpha t</math>,可见<math display="inline">K</math>与上式中的<math display="inline">8\alpha t</math>相近。实际上,<math display="inline">K</math>是<math display="inline">8αt</math>表达式的<math display="inline">^3/_4</math>倍,因此
| |
|
| |
| <math display="block">
| |
| K=\displaystyle-\frac{3}{4}\ln{\left(1-\frac{4d}{3}\right)}
| |
| </math>
| |
|
| |
| 其中<math display="inline">d</math>是观察到两个DNA序列之间差异位点的比例,即<math display="inline">p</math>-距离。<math display="inline">K</math>则是经过Jukes–Cantor核苷酸替换模型校正多重命中后,估计的实际经历分歧事件的位点数。
| |
|
| |
| 几个例子有助于说明Jukes–Cantor模型校正的实际应用。假设两条DNA序列在10个位点中有1个位点不同,则<math display="inline">p</math>-距离为<math display="inline">10\%</math>即<math display="inline">d=0.10</math>。这个观测到的分歧水平是被低估的,因为它没有考虑多重命中。为校正多重命中,我们计算校正后的分歧为:
| |
|
| |
| <math display="block">
| |
| K=\mathrm{-}\frac{3}{4}\ln\left(1-\frac{4}{3}(0.10)\right)=0.1073
| |
| </math>
| |
|
| |
| 这表明在表观分歧度为<math display="inline">10\%</math>时,预计有<math display="inline">0.7\%</math>的位点经历了多重命中。真实分歧度估计为<math display="inline">10.73\%</math>,略高于表观分歧度。若表观分歧度更大,例如<math display="inline">d=0.40</math>,则校正幅度也会更大:
| |
|
| |
| <math display="block">
| |
| K=\mathrm{-}\frac{3}{4}\ln\left(1-\frac{4}{3}(0.40)\right)=0.5813
| |
| </math>
| |
|
| |
| 此时多重命中校正幅度超过<math display="inline">18\%</math>,总校正后的核苷酸位点分歧度达<math display="inline">58.13\%</math>。通常约定大写字母<math display="inline">K</math>表示经过饱和度校正的分歧估计值,而小写<math display="inline">k</math>或<math display="inline">d</math>表示未校正的分歧估计值。
| |
|
| |
| Jukes–Cantor是最简单的核苷酸替换模型,它假设DNA序列中所有核苷酸频率相等,且所有位点具有相同的替换速率。然而许多DNA序列表现出这些参数的变异,而Jukes–Cantor模型未予考虑。现有多种复杂度递增的核苷酸替换模型(Posada和Crandall 2001),通过使用更多参数来表示不同类型的替换速率。图8.14展示了部分核苷酸替换模型的层级结构。这些不同模型可通过检验DNA序列数据来验证模型假设。例如,Jukes–Cantor模型假设所有核苷酸频率相等。若DNA序列样本的碱基频率显著偏离<math display="inline">25\%</math>的等频率,则F81模型是更好的选择,因为它假设任意碱基频率。JC和F81核苷酸替换模型均假设转换与颠换速率相等且替换速率在位点间恒定。当前常规做法是估计最能近似DNA序列数据集核苷酸变化模式的替换模型(Posada和Crandall 1998)。
| |
|
| |
| <span id="通过分离位点和核苷酸多样性测量dna多态性"></span>
| |
| ==== 通过分离位点和核苷酸多样性测量DNA多态性 ====
| |
|
| |
| 同一物种中一个基因座上的可变DNA序列代表了种群中存在的不同等位基因。由于DNA序列由多个核苷酸位点组成,定义等位基因比离散型等位基因的情形更为复杂。假设从种群中获取<math display="inline">n</math>个个体样本,并为每个个体的一个基因或基因组区域测定<math display="inline">L</math>个核苷酸的DNA序列(参见 Tajima 1993b)。为简化起见,将每个个体视为单倍体或纯合体。第一步需要构建多重序列比对,使每条序列的同源核苷酸位点均对齐于同一列(图8.15)。通过这样的多重序列比对,有两种常用指标可用于描述单物种DNA序列样本中的多态性模式。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/1596e301c4983e9f0b2566e792add3769395547d2d952e087f8e1e9388b27e45.jpg]]<br />
| |
| '''Figure 8.14''' 可用于校正DNA序列间表观分歧的核苷酸替代模型层级结构,以更准确估计实际发生的替代数。Jukes-Cantor模型最为简单,假设所有核苷酸变化具有单一且恒定的替代速率。其他核苷酸替代模型通过增加参数数量来体现DNA序列演化的更多特征,特别是不同核苷酸类别间的可变替代速率。若核苷酸替代速率在不同位点间存在差异,可通过伽马分布(以希腊字母<math display="inline">\Gamma</math>表示)建模。核苷酸替代模型包括:<math display="inline">\mathrm{JC}=</math> Jukes-Cantor(Jukes和Cantor 1969),<math display="inline">\mathrm{F}81=</math> Felsenstein 81(Felsenstein 1981),<math display="inline">\mathrm{K}80=</math> Kimura 80(Kimura 1980),<math display="inline">\mathrm{HKY}=</math> Hasegawa-Kishino-Yano(Hasegawa等1985),<math display="inline">\mathrm{SYM}=</math> 对称模型(Zharkikh 1994)以及<math display="inline">\mathrm{GTR}=</math> 广义时间可逆模型(Rodriguez等1990)。来源:改编自Posada和Crandall(1998)的图表。
| |
|
| |
| 衡量DNA多态性的一个指标是'''分离位点数'''<math display="inline">S</math>。分离位点指<math display="inline">L</math>个核苷酸位点中在种群内存在两个或多个核苷酸变异的位点,如图8.15中的位点2、6和8。总分离位点数记为<math display="inline">S</math>,可通过将分离位点数除以总位点数得到每核苷酸位点的分离位点频率<math display="inline">p_{S}</math>:
| |
|
| |
| <math display="block">
| |
| p_{S}={\frac{S}{L}}
| |
| </math>
| |
|
| |
| 某一特定位点上携带特定核苷酸的DNA序列频率不影响<math display="inline">S</math>的计算(比较图8.15中的位点2和6),但<math display="inline">S</math>值会随样本个体数的增加而上升,因为样本中将包含更多携带新多态性的DNA序列。
| |
|
| |
| 在'''中性理论'''下,'''分离位点数量'''(<math display="inline">S</math>)是'''尺度化突变率''' <math display="inline">4N_{e}\upmu</math> 的函数。Watterson(1975)首次提出了一种通过DNA序列样本中观察到的分离位点数量来估计θ的方法。在'''漂变-突变平衡'''下,分离位点的期望数量可通过'''溯祖模型'''(Watterson使用了另一种方法)确定。在'''无限位点突变模型'''下,每次突变发生都会使分离位点数量增加1。因此,分离位点的期望数量即为给定谱系的突变期望数量。若每个谱系每代的突变概率为<math display="inline">\upmu</math>,且有<math display="inline">k</math>个谱系,则单代的期望突变数为<math display="inline">k\upmu</math>。若<math display="inline">k</math>个谱系的合并期望时间为<math display="inline">T_{k}</math>,则每个<math display="inline">k</math>值对应的期望突变数为<math display="inline">k\upmu T_{k}</math>。通过累加从当前到'''最近共同祖先'''(MRCA)间所有<math display="inline">k</math>值的突变数,可得到期望突变总数(<math display="inline">E</math>表示期望或平均值):
| |
|
| |
| <math display="block">
| |
| E[S]=E\left[\sum_{k=2}^{n}\mu k T_{k}\right]=\mu\sum_{k=2}^{n}k E[T_{k}]
| |
| </math>
| |
|
| |
| 其中<math display="inline">n</math>为当前谱系总数。关于此方程的图示可参考图3.25(假设<math display="inline">n=6</math>),并想象在每次合并事件间的时间间隔内累加突变概率。
| |
|
| |
| '''溯祖模型'''的核心结论是:<math display="inline">k</math>个谱系发生合并的概率为<math display="inline">\frac{k(k-1)}{2}\left(\frac{1}{2N_{e}}\right)</math>。因此,合并的期望时间是其概率的倒数,即<math display="inline">\frac{2(2N_{e})}{k(k-1)}</math>。将此期望时间代入方程8.24可得:
| |
|
| |
| <math display="block">
| |
| E[S]=\mu\sum_{k=2}^{n}k\frac{2(2N_{e})}{k(k-1)}
| |
| </math>
| |
|
| |
| 通过约简<math display="inline">k</math>、将常数<math display="inline">4N_{e}</math>提出求和符号,并调整求和范围以消除分母中的<math display="inline">k^{-1}</math>,方程可简化为:
| |
|
| |
| <math display="block">
| |
| E[S]=4N_{e}\mu\sum_{k=1}^{n-1}{\frac{1}{k}}
| |
| </math>
| |
|
| |
| 该式给出了<math display="inline">n</math>条DNA序列样本中分离位点的期望数量。若将<math display="inline">\uptheta{=}4N_{e}\upmu</math>代入方程8.27,可得:
| |
|
| |
| <math display="block">
| |
| E[S]=\theta\sum_{k=1}^{n-1}{\frac{1}{k}}
| |
| </math>
| |
|
| |
|
| |
| -----
| |
|
| |
| {|
| |
| !width="47%"| Sequence1 Sequence2 Sequence3 Sequence4
| |
| !width="52%"| AATGTCAACG AATGTCAACG ATTGTCAACG ATTGTGATCG
| |
| |-
| |
| |
| |
| | 羊 * *
| |
| |-
| |
| | Sitenumber
| |
| | 12345678910
| |
| |}
| |
|
| |
|
| |
| -----
| |
|
| |
| {|
| |
| !width="100%"| Segregating sites (S and ps):
| |
| |-
| |
| | Sites 2, 6, and 8 have variable base pairs among the four sequences (columns marked with *). These are segregating sites. Therefore, for these sequences, S=3 segregating sites and ps =3/10 =0.3 segregating sites per nucleotide site examined.
| |
| |}
| |
|
| |
| {|
| |
| !width="100%"| Nucleotide diversity (π):
| |
| |-
| |
| | 1AATGTCAACG d12= 0 2 2AATGTCAACG
| |
| |}
| |
|
| |
| {|
| |
| !width="36%"| AATGTCAACG 3 ATTGTCAACG
| |
| !width="18%"| 3ATTGTCAACG
| |
| !width="13%"| d23 = 1
| |
| !width="18%"| 3ATTGTCAACG
| |
| !width="13%"| d34 = 2
| |
| |}
| |
|
| |
| {|
| |
| !width="100%"| 1 AATGTCAACG d14 = 3 :2 AATGTCAACG d24 =3 4ATTGTGATCG 4ATTGTGATCG 4ATTGTGATCG
| |
| |}
| |
|
| |
| {|
| |
| !width="100%"| ∑dij = 0 + 1 + 3 + 1 + 3 + 2 = 10 number of pairs of sequences compared=[n(n-1)]/2=[4(3)]/2=6 =10 differences/6 pairs =1.67 average pairwise differences
| |
| |}
| |
|
| |
| 分离位点数量的方差是突变过程(泊松分布,方差等于均值)和溯祖过程(指数分布,方差为期望值的平方)导致的方差之和,由于两个过程独立,协方差为零:
| |
|
| |
| <math display="block">
| |
| \operatorname{var}(S)=\theta\sum_{k=1}^{n-1}{\frac{1}{k}}+\theta^{2}\sum_{k=1}^{n-1}{\frac{1}{k^{2}}}
| |
| </math>
| |
|
| |
| 在中性模型中,由于溯祖时间和突变事件的联合随机变异,分离位点数量的方差相当显著。
| |
|
| |
| 一旦已知分离位点数的期望值<math display="inline">E[S]</math>,即可通过重新整理方程8.28来估计尺度化突变率θ:
| |
|
| |
| <math display="block">
| |
| \theta=\frac{E[S]}{\displaystyle\sum_{k=1}^{n-1}\frac{1}{k}}
| |
| </math>
| |
|
| |
| 第二种DNA多态性测量指标是DNA序列样本中的核苷酸多样性,符号为<math display="inline">\pi</math>(发音”pie”)或有时写作<math display="inline">\uptheta_{\pi}</math>,也称为DNA序列样本中平均成对差异(Nei和Li 1979;Nei和Kumar 2000)。核苷酸多样性等同于用DNA序列表示的等位基因测得的杂合度(假设随机交配和无限位点突变模型)。核苷酸多样性通过比较样本中每对独特DNA序列时发现的核苷酸位点差异数的平均值,来总结核苷酸多态性。与分离位点比例不同,核苷酸多样性对样本中各DNA序列等位型的频率敏感,因为更频繁出现的序列会参与更多的成对比较。核苷酸多样性是每对DNA序列间核苷酸差异数的总和:
| |
|
| |
| 通过将分离位点数除以谱系总分支长度来求解θ。如果我们定义新变量<math display="inline">a_{1}=\sum_{k=1}^{n-1}{\frac{1}{k}}</math>,并用<math display="inline">\hat{S}</math>代替<math display="inline">E[S]</math>,则:
| |
|
| |
| <math display="block">
| |
| \hat{\theta}_{S}=\frac{\hat{S}}{a_{1}}
| |
| </math>
| |
|
| |
| 使用分离位点绝对数,或:
| |
|
| |
| <math display="block">
| |
| {\hat{\theta}}_{S}={\frac{{\hat{p}}_{S}}{a_{1}}}
| |
| </math>
| |
|
| |
| 使用每核苷酸位点观察到的分离位点数。将<math display="inline">a_{1}</math>的定义代入方程8.29,可以得到<math display="inline">\hat{\boldsymbol{\theta}}_{S}</math>的方差表达式:
| |
|
| |
| <math display="block">
| |
| \mathrm{var}\big(\hat{\theta}_{S}\big)=\hat{\theta}_{S}a_{1}+\hat{\theta}_{S}^{2}\sum_{k=1}^{n-1}\frac{1}{k^{2}}
| |
| </math>
| |
|
| |
| 其中:
| |
|
| |
| <math display="block">
| |
| \hat{\pi}=\frac{1}{\frac{n(n-1)}{2}}\Sigma_{i=1}^{n}{\Sigma_{j}^{n}}_{>i}d_{i j}
| |
| </math>
| |
|
| |
| 式中i和<math display="inline">j</math>表示个体DNA序列的索引,<math display="inline">d_{i j}</math>是序列i和<math display="inline">j</math>间差异的核苷酸位点数,<math display="inline">n</math>是样本中DNA序列总数。<math display="inline">n</math>条序列样本中独特的成对比较数为<math display="inline">(n[n-1])/2</math>,因此将<math display="inline">d_{i j}</math>之和除以该数可得每对序列的平均差异数。平均成对差异数也可除以检测的核苷酸位点数<math display="inline">(L)</math>以表示每核苷酸位点的<math display="inline">\hat{\pi}</math>。图8.15展示了四个假设DNA序列样本的<math display="inline">\hat{\pi}</math>计算示例。
| |
|
| |
| <pre class="markdown">根据样本DNA序列中分离位点数量估算的标化突变率有时用$\hat{\boldsymbol{\theta}}_{W}$表示(W代表Watterson)。这两个最终量的重要性在于,$4N_{e}\upmu$及其在标准中性模型下的方差可以通过样本中观察到的分离位点数量进行估计。
| |
|
| |
| 在可能包含多个相同DNA序列的大样本中,核苷酸多样性可通过下式估计:
| |
|
| |
| $$
| |
| {\hat{\pi}}={\frac{k}{k-1}}\Sigma_{i=1}^{k}{\Sigma}_{j=i}^{k}p_{i}p_{j}d_{i j}=2{\frac{k}{k-1}}\Sigma_{i=2}^{k}\Sigma_{j=i}^{i-1}p_{i}p_{j}d_{i j}
| |
| $$
| |
|
| |
| 其中$p_{i}$和$p_{j}$分别代表样本中$k$个不同序列(每个序列代表一个等位基因)的第$i$和第$j$等位基因频率。方程的第一个版本对等位基因对间差异数矩阵的所有元素求和,包括对角线元素。第二个版本是对下三角元素求和的两倍。由于$d_{i i}$元素均为零,这两个版本等价。该公式通过对样本中各类型DNA序列频率的加权求和,提供了$d_{i j}$的平均值。若群体中存在未被采样的稀有序列多态性,核苷酸多样性可能被低估(参见Renwick等,2003)。$\uppi$的抽样方差信息可参考Nei和Kumar(2000)。
| |
|
| |
| 表8.1 不同生物和基因座的DNA序列多态性比较研究报道的核苷酸多样性(π)估计值。所有估计值为每个核苷酸位点的平均成对核苷酸差异。例如,$\pi=0.02$表示样本中所有DNA序列对间每100个位点有2个差异。
| |
|
| |
| | Species | Locus | π | References |
| |
| |------------------------------|--------------|--------------|------------------------|
| |
| | _Drosophila melanogaster_ | anon1A3 | 0.0044 | Andolfatto (2001) |
| |
| | | Boss | 0.0170 | |
| |
| | _Drosophila simulans_ | transformer | 0.0051 | |
| |
| | | anon1A3 | 0.0062 | |
| |
| | | Boss | 0.0510 | |
| |
| | | transformer | 0.0252 | |
| |
| | _Caenorhabditis elegans_a | tra-2 | 0.0 | Graustein et al. (2002)|
| |
| | _Caenorhabditis remane_p | glp-1 | 0.0009 | |
| |
| | | IO | 0.0102 | |
| |
| | | tra-2 | 0.0112 | |
| |
| | | glp-1 | 0.0188 | |
| |
| | | | 0.0228 | |
| |
| | | CAUL | | Wright et al. (2003) |
| |
| | _Arabidopsis thaliana_a | ETR1 | 0.0042 0.0192| |
| |
| | | RbcL | 0.0012 | |
| |
| | | CAUL | 0.0135 | |
| |
| | _Arabidopsis lyrata_ ssp. _petraea_b | ETR1 | | |
| |
| | | RbcL | 0.0276 0.0013| |
| |
|
| |
| ^a 自交繁殖物种
| |
| ^b 异交繁殖物种</pre>
| |
| 表8.1展示了来自不同生物和基因座的π值。核苷酸多样性(nucleotide diversity)的估计是有用的,因为π是DNA序列杂合度的度量。因此,在遗传漂变(genetic drift)和突变(mutation)的平衡下,π的值是<math display="inline">4N_{e}\upmu</math>的函数。通过π的估计和基因座突变率(μ),可以估计有效种群大小。由于π是标准化突变率θ的估计量,有时也被称为<math display="inline">\hat{\boldsymbol{\theta}}_{\pi}</math>。
| |
|
| |
| <span id="互动框8.3-从dna序列数据估计π和s"></span>
| |
| = 互动框8.3 从DNA序列数据估计π和S =
| |
|
| |
| 通过多个DNA序列样本估计分离位点数量(S)和核苷酸多样性或平均成对差异(π)是一个有价值的练习。
| |
|
| |
| 第一步是从Genbank获取DNA序列数据。教材网页提供了分步说明,以获取30头非洲黑马羚(''Hippotragus niger'')线粒体细胞色素<math display="inline">b</math>基因的DNA序列(Pitra等,2002)。这30条序列需先进行多序列比对,然后利用比对后的序列估计分离位点数量(S)和平均成对差异(π)。
| |
|
| |
| <math display="inline">\uptheta_{\pi}</math>和<math display="inline">\uptheta_{\mathrm{S}}</math>的度量基于量化序列多态性位点频谱(site frequency spectrum)的通用方法。样本中<math display="inline">n</math>条序列的分离位点可根据共享每个等位类型的序列数量进行分类(Fu,1995,1997)。这描述了谱系中<math display="inline">2(n-1)</math>条分支,因为具有共同等位状态的分离位点共享谱系的同一分支。分离位点可被分类为等位状态出现i次或<math display="inline">n{-}i</math>次的单倍型。变量<math display="inline">\xi_{\mathrm{i}}</math>(小写希腊字母xi)表示单倍型(或突变型)出现i次或<math display="inline">n{-}i</math>次的分离位点数量。Fu(1995)证明,分离位点数量是标准化突变率θ的函数:<br />
| |
| <math display="inline">\begin{array}{r}{E[\xi_{i}]=\frac{1}{i}\theta}\end{array}</math><br />
| |
| 其中i在1到<math display="inline">n{-}1</math>之间(样本量为<math display="inline">n</math>条序列)。以图8.15中<math display="inline">n=4</math>条序列为例,假设序列1为祖先序列以计数衍生等位状态,则位点6和8各有一个衍生核苷酸状态的单倍型,对应<math display="inline">\xi_{1}=2</math>;位点2有两个衍生核苷酸状态的单倍型,对应<math display="inline">\xi_{2}=1</math>;而<math display="inline">\xi_{3}=0</math>,因为没有位点存在三个衍生核苷酸状态的单倍型。
| |
|
| |
| 本节前文提到的两种序列多态性度量可表示为<math display="inline">\xi</math>的函数:<br />
| |
| <math display="block">
| |
| \hat{\theta}_{S}=\frac{1}{a_{1}}\sum_{i=1}^{n-1}\xi_{i}
| |
| </math><br />
| |
| 和<br />
| |
| <math display="block">
| |
| {\hat{\theta}}_{\pi}={\frac{2}{n(n-1)}}\sum_{i=1}^{n-1}i(n-i)\xi_{i}
| |
| </math>
| |
|
| |
| 另外两种序列多态性度量可被构建,分别对高频单倍型:<br />
| |
| <math display="block">
| |
| \hat{\theta}_{H}=\frac{1}{a_{2}}\sum_{i=1}^{n-1}i^2\xi_{i}
| |
| </math><br />
| |
| 或低频单倍型:<br />
| |
| <math display="block">
| |
| \hat{\theta}_{L}=\frac{1}{n-1}\sum_{i=1}^{n-1}i\xi_{i}
| |
| </math><br />
| |
| 赋予更高权重。这些度量捕捉了序列多态性的不同方面,并用于假设检验中分析作用于序列多态性的演化过程(本章后续将描述)。
| |
|
| |
| <span id="dna序列分歧与分子钟"></span>
| |
| ==== 8.4 DNA序列分歧与分子钟 ====
| |
|
| |
| 分子钟假说<br />
| |
| 用分子钟测定分歧事件的时间
| |
|
| |
| 中性理论的一个关键结果是预测替换率等于突变率。这一预测的一个推论是,替换之间的预期世代数为突变率的倒数。例如,若每世代每个复制碱基对的突变率为<math display="inline">1\times{10}^{-5}</math>,则我们预计平均需要等待<math display="inline">10^{5}</math>世代才能在一个基因拷贝中观测到一个突变。因此,中性理论为隔离种群或物种间同源基因或基因组区域的分化速率提供了一个零模型,称为分子钟假说。本节将首先展示证明分子钟存在的数据,接着说明如何利用分子钟假说基于DNA分化来推断进化事件的发生时间,最后解释为何随着时间推移和众多替换的积累,表观分化度可能降低,以及如何通过突变过程模型对分化度估计值进行校正。
| |
|
| |
| <math display="block">
| |
| \hat{\theta}_{H}=\frac{2}{n(n-1)}{\sum_{i=1}^{n-1}i^{2}\xi_{i}}
| |
| </math>
| |
|
| |
| 正如”钟”的隐喻所示,分子钟假说预测分化会随时间推移以均匀规律性积累,如同钟表的滴答声。这意味着两个物种间的分化度应随着它们最近共同祖先存在时间的久远而增加。这种模式最初由Zuckerkandl和Pauling(1962,1965)在血红蛋白中观察到,他们首次提出了分子钟假说。分子钟的经典案例可见于人甲型流感病毒NS基因中分化度随时间增加的现象(图8.16)。Buonagurio等(1986)使用1933至1986年间采集的流感病毒样本,通过计算每个序列与推断祖先序列间的核苷酸替换数(即''p''-distance),发现分化度随时间呈线性增长,这与分子钟假说的预测一致。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/99232c5d471a2e2044b87ed7b94be92eca722f7f11686dd86e3607d936a03114.jpg]]<br />
| |
| 图8.16 基于1933至1985年间分离的11个人类甲型流感病毒样本,编码”非结构”蛋白的NS基因核苷酸变化速率。自分离后的年数与DNA序列相对于推断共同祖先的分化度呈正相关。随着分歧时间增加而出现的替换数增长模式符合分子钟假说的预期。观测到的替换速率约为每年每个核苷酸位点<math display="inline">1.9\times{{10}^{-3}}</math>次替换,远高于真核生物大多数基因的速率。直线为最小二乘拟合。数据来源:Buonagurio等(1986)。
| |
|
| |
| 分子钟假说:中性理论预测分化应随时间以恒定速率发生,使得物种间分子分化程度与其分离时间成正比,与速率恒定性(rate constancy)或速率同质性(rate homogeneity)同义。
| |
|
| |
| 分子钟的另一个重要早期进展出现在Richard Dickerson(1971)比较细胞色素<math display="inline">c</math>、血红蛋白和纤维蛋白肽基因的蛋白质替换速率时。他观察到这三种蛋白质的平均变化速率存在显著差异(图8.17)。基于当时对这些蛋白质功能的了解,Dickerson提出:当更少的位点受到氨基酸变化的功能性约束时,分子进化的速率更快。也就是说,当更多位点呈中性且可通过遗传漂变自由演化时,分子进化速度更快;而当更大比例的氨基酸变化因降低或消除蛋白质功能而被自然选择淘汰时,分子进化速度更慢。因此,物种间序列未发生分化的位点可能是由于功能的选择性约束而保持恒定。在这种当时新颖的观点下,蛋白质或DNA序列中随时间不变且物种间共享的区域暗示着功能重要性区域。中性理论成为解释不同位点可能具有不同速率的分子钟的关键概念。
| |
|
| |
| ==== 利用分子钟进行事件定年 ====
| |
|
| |
| 分子钟的一个重要应用是确定物种间的分歧事件时间。对某些生物而言,化石记录和地质背景可提供物种起源、灭绝或演化转变的时间节点。然而,许多类群的生物缺乏化石记录,且并非所有表型都能形成化石,这为生物事件定年带来了挑战。若已知两个物种间的DNA序列分歧量,则可利用该信息推算其分歧时间。分子钟假说主张:对于中性等位基因,替换速率等于突变速率,即<math display="inline">k=\mu</math>。若已知以单位时间内固定次数表示的绝对替换速率,将该速率乘以时间即可得到预期的替换次数。两个物种间的分化核苷酸位点数也以两倍替换速率累积,因为每个谱系独立经历替换过程。结合这两个观察结果可得:
| |
|
| |
| <math display="block">
| |
| k=2T\mu
| |
| </math>
| |
|
| |
| 该式表示两个物种在<math display="inline">T</math>时间单位前的预期分歧量。若两个物种间的分歧量以及【“fixations”译为“固定次数”】
| |
|
| |
| '''图8.17''' 纤维蛋白肽、血红蛋白和细胞色素<math display="inline">c</math>在极长时间尺度上以每100个残基的氨基酸变化表示的蛋白质进化速率。如分子钟预期,每种蛋白质的分歧速率随时间呈线性关系。不同蛋白质因突变速率和自然选择施加的功能约束程度不同而具有不同的钟速。对于分歧时间未知的分类群对,其氨基酸变化绘制在虚线上,这些虚线与通过已知分歧时间分类群数据点的实线具有相同斜率。血红蛋白图中六个未知分歧时间的点代表最早动物中祖先珠蛋白分化为血红蛋白和肌红蛋白的事件,分子钟估计这些事件发生在11亿至8亿年前。来源:数据来自Dickerson(1971)。另见Robinson等(2016)。
| |
|
| |
| 若已知分歧时间,此关系可重新排列以求解未知时间:
| |
|
| |
| <math display="block">
| |
| T={\frac{k}{2\mu}}
| |
| </math>
| |
|
| |
| '''绝对替换速率''':基于两个分类群的序列分歧估计及其分歧时间的估计,以每年替换次数计算的分子变化速率。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/382eacf747847e6073ebf38cf1fbad0a6e192557b573631e08536218e321c39c.jpg]]<br />
| |
| '''图8.18'''展示了包含三个分类群和两个分歧时间的情形。利用分子钟进行事件定年需要估计每对物种间的核苷酸分歧(经饱和调整)(<math display="inline">\mathit{\Omega}^{\prime}K_{\mathrm{AB}}</math>、<math display="inline">\mathit{K}_{\mathrm{AC}}</math>和<math display="inline">K_{\mathrm{BC}}</math>)并已知一个分歧时间。假设我们的目标是确定物种<math display="inline">\mathrm{A}</math>和B的分歧时间<math display="inline">(T_{2})</math>,已知分歧时间<math display="inline">T_{1}</math>。可通过已知分歧时间估计发生的绝对替换速率:
| |
|
| |
| '''图8.18''' 在假设分歧速率随时间恒定(分子钟)条件下可用于确定分歧事件的系统发育树示意图。<math display="inline">T_{1}</math>是物种C与物种A和B祖先分化的过去时间,<math display="inline">T_{2}</math>是物种A和B分化的过去时间。若已知<math display="inline">T_{1}</math>或<math display="inline">T_{2}</math>,则可通过观察到的序列分歧估计单位时间的分子进化速率,进而用此分歧速率估计其他分歧事件经历的未知时间。
| |
|
| |
| <math display="block">
| |
| \mu={\frac{1}{2}}\left({\frac{K_{\mathrm{AC}}}{2T_{1}}}+{\frac{K_{\mathrm{BC}}}{2T_{1}}}\right)
| |
| </math>
| |
|
| |
| 此速率基于物种对A和C<math display="inline">(K_{\mathrm{AC}})</math>及物种对B和C<math display="inline">(K_{\mathrm{BC}})</math>观察到的平均分歧与分歧时间<math display="inline">T_{1}</math>。随后可用此速率求解未知分歧时间<math display="inline">T_{2}</math>:
| |
|
| |
| <math display="block">
| |
| T_{2}=\frac{K_{\mathrm{AB}}}{2\mu}
| |
| </math>
| |
|
| |
| 将式8.42中<math display="inline">\mu</math>的定义代入后,式8.43变为:
| |
|
| |
| <math display="block">
| |
| T_{2}={\frac{2T_{1}K_{\mathrm{AB}}}{K_{\mathrm{AC}}+K_{\mathrm{BC}}}}
| |
| </math>
| |
|
| |
| 例如,假设DNA序列分歧度估计为<math display="inline">K_{\mathrm{AB}}=0.10</math>、<math display="inline">K_{\mathrm{AC}}=0.31</math>和<math display="inline">K_{\mathrm{BC}}=0.36</math>每个位点的替换数,且分歧时间<math display="inline">T_{1}</math>通过化石和地质数据估计为10百万年。那么时间间隔<math display="inline">T_{2}</math>的估计值为:
| |
|
| |
| <math display="block">
| |
| T_{2}=\frac{2({\mathrm{10}}{\mathrm{million}}{\mathrm{years}})({\mathrm{0.10}}{\mathrm{substitutions}}{\mathrm{per}}{\mathrm{site}})}{({\mathrm{0.31}}{\mathrm{substitutions}}{\mathrm{per}}{\mathrm{site}})+({\mathrm{0.36}}{\mathrm{substitutions}}{\mathrm{per}}{\mathrm{site}})}
| |
| </math>
| |
|
| |
| 这个结果符合直觉。物种A与B之间的DNA分歧度约为A-B与A-C物种对平均DNA序列分歧度的三分之一。由于A、B、C在10百万年前从共同祖先分化,因此当A与B分化时的<math display="inline">T_{2}</math>时间约为该时间的三分之一。这些时间估计的假设是:替换速率在时间、谱系和位点间保持恒定。这些假设将在本章后续进行批判性讨论。
| |
|
| |
| 分子钟已被广泛用于确定重大演化转变的时间,建立多种生物祖先首次演化的时间框架,并检验与分歧时间相关的假说(Hedges et al. 2015综述)。一个例子是检验”早期哺乳动物演化因恐龙灭绝后开放的生态位而促进”的假说。分子钟表明,最早的哺乳动物谱系在恐龙灭绝完成前早已出现(Bromham et al. 1999;Bininda-Emonds et al. 2007)。因此,估计的分歧时间不支持”哺乳动物在恐龙消失后占据空置栖息地时演化”的假说。
| |
|
| |
| <span id="问题框-8.1-用分子钟估计分歧时间"></span>
| |
| = 问题框 8.1 用分子钟估计分歧时间 =
| |
|
| |
| 现今,双子叶植物是陆生植物的主体。祖先种子植物分化为单子叶植物和双子叶植物的过程是重要的演化转变。基于多种植物中9个线粒体基因同义位点的DNA分歧数据(Laroche et al. 1995),可用分子钟测定该事件的时间。
| |
|
| |
| 表8.2给出了单子叶植物玉米与小麦(估计分歧时间约60百万年前)的DNA分歧数据。首先用玉米-小麦DNA分歧数据校准每个基因座每百万年的绝对替换速率,然后用该替换速率根据DNA序列分歧度估计单子叶与双子叶植物的分化时间。参照图8.18,玉米-小麦分化对应<math display="inline">T_{2}</math>,而单子叶-双子叶分化对应<math display="inline">T_{1}</math>。
| |
|
| |
| 表8.2 单子叶植物玉米与小麦三个基因座的DNA分歧度估计
| |
|
| |
| {|
| |
| !width="7%"| Locus
| |
| !width="12%"| 核苷酸位点
| |
| !width="11%"| 同义位点
| |
| !width="31%"| 每个位点的替换数(小麦-玉米)
| |
| !width="36%"| 每个位点的替换数(单子叶-双子叶)
| |
| |-
| |
| | coxl
| |
| | 1461
| |
| | 495
| |
| | 0.0504
| |
| | 0.2060
| |
| |-
| |
| | atp9
| |
| | 195
| |
| | 67
| |
| | 0.1374
| |
| | 0.4439
| |
| |-
| |
| | nad4
| |
| | 1272
| |
| | 456
| |
| | 0.0381
| |
| | 0.1101
| |
| |}
| |
|
| |
| 第二个例证是关于人类及其近亲祖先何时分异的经典问题。Glazko和Nei(2003)利用红毛猩猩(''Pongo'')与人类分异时间为1300万年,以及偶蹄目(具有偶数趾的有蹄类哺乳动物,如牛、鹿和猪)与灵长类分异时间为9000万年的校准时间点,结合多基因座数据,估算出人类与黑猩猩(''Pan'')的分异时间发生在500-700万年前。针对灵长类开展的更多分子钟研究表明,不同谱系间以及各类可能影响分子钟推断时间的基因组变化类型之间,存在替换速率的变异证据。
| |
|
| |
| Moorjani等(2016)发现,10个灵长类谱系的全基因组分子钟显示,CpG位点(胞嘧啶核苷酸后接鸟嘌呤核苷酸的位点)的替换速率具有最高的一致性。仅使用CpG位点的分子钟模型估算得出人类与黑猩猩分异时间为1210万年前。有证据表明,与猩猩(''Gorilla'')和黑猩猩相比,人类谱系近期经历了更缓慢的分子钟速率,这会延长分子钟估算的分异时间,使其与化石证据更为吻合(Scally和Durbin 2012;Besenbacher等 2019)。
| |
|
| |
| 第三个例子是利用分子钟来测定人类免疫缺陷病毒(HIV)的起源时间。HIV从灵长类传播到人类的日期一直是理解该病毒起源及其进化变化模式的关键问题,以预防未来可能从动物到人类的疾病传播。关于HIV起源的主要假说认为,猿免疫缺陷病毒(''SIV'')的'''单倍型'''感染了那些狩猎灵长类并处理其尸体的人类。尽管存在重组事件、某些核苷酸变化的自然选择,以及因病毒样本采集时间不同而进行的采样日期调整,HIV-1的DNA序列替换速率仍表现出类似钟表的替换模式(Leitner and Albert 1999; Salemi et al. 2001; Liu et al. 2004; Park et al. 2016)。分子钟的应用表明,HIV-1 M亚型——在人类中引发大流行的单倍型——于1920年代传入人类。HIV的分子钟现已被用于详细重建该病毒在刚果民主共和国金沙萨(当时称扎伊尔)的地理起源和早期传播,以及随后在非洲和全球的扩散(见Faria et al. 2014)。(关于HIV最初通过被污染的脊髓灰质炎疫苗传播给人类的争议性假说——该疫苗由培养的黑猩猩细胞制成,并于1957至1960年间在前比利时刚果使用——与HIV-1的分子钟分歧时间估计不一致,且被其他直接证据反驳(Cohen 2001; Worobey et al. 2004))。系统发育和分子钟证据还表明,灵长类中传播的''SIV''谱系曾两次跳跃到人类:HIV-1谱系与黑猩猩的''SIV''亲缘关系最近,而HIV-2谱系与乌白眉猴的''SIV''亲缘关系最近(Gao et al. 1992; Lemey et al. 2003; Keele et al. 2006)。
| |
|
| |
| 分子钟用于估计分歧时间时,在实践中常受诸多问题影响(Arbogast et al. 2002综述),导致日期估计存在统计学不确定性。首先,校准时间通常具有较大范围,导致分子钟估计的任何分歧时间都存在不确定性。此外,替换速率随时间的变化……
| |
|
| |
| <span id="互动框8.4-分子钟对进化事件的估计"></span>
| |
| = 互动框8.4 分子钟对进化事件的估计 =
| |
|
| |
| TimeTree(Kumar et al. 2017)是一个可搜索的生命之树数据库,汇集了利用分子钟测定进化事件的研究结果。该项目允许用户估算一对分类群的分歧时间、生成时间标定的系统发育树,或查看显示在地质时间线上的系统发育模式。该项目已收集了近100,000个物种的信息并持续更新,目标是呈现完整的生命之树。
| |
|
| |
| 访问TimeTree网站并查看一对物种(如人类和黑猩猩)的分歧时间估计(Node Time)。使用Timetree功能查看类群(如灵长类)的分歧时间。接着,探索您选择的其他分类群的时间估计。
| |
|
| |
| <span id="检验分子钟假说及分子进化中速率变异的解释"></span>
| |
| ==== 8.5 检验分子钟假说及分子进化中速率变异的解释 ====
| |
|
| |
| 分子钟的速率异质性<br />
| |
| 业 分子钟的泊松过程模型。祖先多态性与分子钟。<br />
| |
| 分子钟的相对速率检验。速率异质性的可能成因。
| |
|
| |
| 分子钟预测,在具有相同突变速率的选择中性同源序列(指通过共同祖先遗传曾经完全相同的序列)中,随着分歧时间的增加,单位时间内经历的替换数量应当相似。因此,分子钟假说为研究分子进化过程中运作的机制提供了一个零模型。我们可以直接检验分子钟假说,从而验证这一零模型。拒绝分子钟假说意味着被比较的序列以不均衡的速率演化,这种情况被称为'''速率异质性'''。拒绝分子钟假说是识别影响替换概率过程的一种方法——这些过程使得固定速率高于或低于仅由遗传漂变预期的水平。例如,前文展示了自然选择如何改变固定概率,从而改变替换速率。因此,比较两个群体时:一个群体中大部分突变是有害的并被选择淘汰,另一个群体中大部分突变是中性的——两者的替换速率会不同,在固定时间间隔内会显示不同的替换数量(见图8.3)。因此,检验替换速率的均一性(速率同质性)是识别分子进化潜在机制的重要步骤。
| |
|
| |
| '''速率异质性''':同源基因组区域在不同时间或不同谱系间发生的替换速率变异。
| |
|
| |
| ==== 分子钟与速率变异 ====
| |
|
| |
| 在谱系间、不同基因座间以及不同类型突变变化间的速率差异现已被视为常态而非例外,这使得估算分歧时间所需的方法更加复杂。分子钟领域的最新进展基于贝叶斯方法对溯祖时间的估算(综述见dos Reis等2016)。这些方法具有多重优势:可通过多种方式建模替换速率的变异、利用化石证据赋予节点年代的先验概率,以及结合序列数据与表型数据进行估算。替换速率的变异将在下一节进一步探讨。
| |
|
| |
| 由于中性理论引出了分子钟假说,速率异质性的证据似乎表明遗传漂变并非导致大多数突变最终替换的主要过程。拒绝速率同质性的假说将意味着自然选择作用于突变,使得它们的替换速率相较于遗传漂变下的替换速率被加速或减缓。新突变通过自然选择固定的概率取决于选择系数''s''和有效种群大小,而非像遗传漂变那样仅取决于<math display="inline">\frac{1}{2N_{e}}</math>。因此,自然选择极不可能产生分子钟,因为''s''、<math display="inline">N_{e}</math>和<math display="inline">\upmu</math>随时间或不同谱系保持恒定的可能性很低。然而,在得出自然选择解释所有速率异质性的结论之前,有必要更深入地探究分子钟假说。分子钟可能比本章开头揭示的更为复杂。理解这些复杂性是理解可能解释分子进化速率异质性的替代假说范围的必要前提。
| |
|
| |
| 分子钟最初由Zuckerkandl和Pauling(1962, 1965, Zuckerkandl 1987)提出,用于模拟氨基酸替换。它基于一种简单的统计方法,用于描述以特定速率随机发生的事件(这类模型称为点过程)。分子钟最简单的点过程是泊松过程——一种用事件计数<math display="inline">N(t)</math>(自时间等于0起)定义【“stochastic process”译为”随机过程”】的随机过程。在泊松过程中,两个时间段内事件数的期望服从泊松分布。假设所有替换都是独立事件、替换概率极小且时间间隔数极大时,泊松钟给出的经过时间段''t''后观察到若干次替换的概率为:
| |
|
| |
| <math display="block">
| |
| \mathrm{Probability}(N(t)\mathrm{\ substitutions\ at\ time\ }t)=\frac{e^{-\lambda t}(\lambda t)^{N(t)}}{N(t)!}
| |
| </math>
| |
|
| |
| 其中<math display="inline">N(t)</math>是总替换次数(整数),<math display="inline">t</math>是以年为单位的时长,λ是每年替换速率。该模型中,时间''t''时的期望替换次数为λt,即替换速率与经过的时间步数的乘积。该模型的关键在于替换速率<math display="inline">\uplambda</math>恒定,既不随时间改变,也不随总替换次数<math display="inline">N(t)</math>改变。图8.19展示了泊松分子钟的运作机制:上图显示当替换速率为<math display="inline">\uplambda=4</math>时,单时间步内<math display="inline">N(t)</math>取值0至14的概率分布;下图8.15展示了在相同时长和恒定替换速率<math display="inline">(\uplambda=4)</math>下,五个复制序列间替换次数的变异情况。
| |
|
| |
| 分子钟的'''Poisson模型'''意味着替换之间的时间间隔在长度上是随机的(图8.20)。因此,遵循Poisson分子钟的替换将被不同长度的时间间隔分隔。这与我们日常的钟表概念形成对比——日常钟表中每个事件(秒、分、时)之间的时间间隔是均匀的。因此,基于随机过程的分子钟即使在替换速率恒定的情况下,也会在给定时间间隔内产生的替换数量上存在固有变异。这意味着从同一祖先同时分化的独立谱系之间,可能表现出不同数量的替换积累。换言之,如果替换是随机过程,那么即使分化时间和替换速率恒定,我们仍预期不同谱系和位点间的替换数量存在变异。这种对替换数量变异的解释常被称为分子进化速率遵循'''Poisson钟'''。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/6191dd2b3d7c6d88de6c2149cebaad6a104dbc2ef3764d0671dc189f584340cb.jpg]]<br />
| |
| '''图8.19''' Poisson过程下的替换模式。上图显示了一个时间间隔内可能发生的替换数量的概率分布。<math display="inline">N(t)</math>在0到9之间的所有值概率均大于0.01。下图展示了五个独立试验中Poisson过程下的累积替换数。每个试验类似于经历替换的独立谱系。平均替换数约为40(时间间隔数乘以4),但谱系间存在变异。两图中的替换速率均为<math display="inline">\lambda=4</math>。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/6103d4f7b52c2bb70610ebb0f64bbdf3887c493d0f1f8c93630eb29765027b9d.jpg]]<br />
| |
| '''字面时钟(突变间时间无变异)'''<br />
| |
| '''图8.20''' 替换事件(圆圈)随时间发生速率的两种表示形式。突变可能以节拍器般的规律性发生,显示突变事件间的时间间隔变异极小。如果替换是随机过程,另一种观点认为替换间的时间间隔是随机变量。Poisson分布常被用于建模特定时间间隔内发生的事件数,因此下图常被称为'''Poisson分子钟'''。注意两种情况下,替换总数与经过的时间相同,因此平均替换速率是等同的。
| |
|
| |
| 分子钟的泊松过程模型对替换数的变异提出了一个特定预测:若分子进化速率遵循泊松过程,则替换数的观测值应满足该预测。泊松分布具有均值等于方差的特殊性质。因此,在相同速率下按照泊松过程独立进化的DNA序列,其替换数的均值与方差应当相等。用于比较替换数均值与方差的比值称为分散指数(index of dispersion),定义为
| |
|
| |
| <math display="block">
| |
| R(t)={\frac{\mathrm{variance}N(t)}{E(N(t))}}
| |
| </math>
| |
|
| |
| 其中<math display="inline">E</math>表示期望值或均值。分散指数定义了泊松过程下预期存在的分歧估计值的离散程度,正如马尔可夫链定义了有限群体集合中预期的等位基因频率分布范围。若成对序列分歧的替换数样本遵循泊松分子钟模型,则替换数的方差与均值应相等,因此<math display="inline">R(t)</math>应等于1。若方差大于均值,则<math display="inline">R(t)</math>大于1,这种情况称为过度分散的分子钟(overdispersed molecular clock),因为替换速率的取值范围比泊松过程模型的预测更广(Culter 2000a综述)。
| |
|
| |
| 过度分散的分子钟(Overdispersed molecular clock):来自多对独立物种的绝对分歧速率总体表现出比泊松过程分子钟模型预期更大的速率方差;其分散指数值大于1。
| |
|
| |
| <span id="ancestral-polymorphism-and-poisson-process-molecular-clock"></span>
| |
| ==== Ancestral polymorphism and poisson process molecular clock ====
| |
|
| |
| = 分子钟 =
| |
|
| |
| 被建模为泊松过程的分子钟假设,可以比较从过去某个单一DNA序列衍生而来、随后立即分化成两个完全隔离物种的DNA序列对。实际的DNA序列通常具有更复杂的历史,这包括祖先物种中运行的过程以及随后在两个独立物种中的分化过程(图8.21)。在祖先物种中,每个位点的中性等位基因数量和频率是由群体过程(如遗传漂变和突变)引起的(假设祖先物种是panmictic【“panmictic”译为“随机交配”】的)。这种祖先多态性区域是指祖先物种中遗传变异由漂变-突变平衡主导的时间段。在此祖先群体内,两个谱系在某一时间点分裂,并最终成为两个独立物种中的谱系(图8.17)。这些两个谱系的DNA序列在现生种中被采样以估计替换率。
| |
|
| |
| 认识到这种更复杂的DNA序列分化历史表明两点。首先,它指出谱系和物种可能在时间上的不同节点分化,且谱系的分化通常早于物种的分化。其次,它表明当在现生种中观察时,两个不同的过程可能导致序列间核苷酸差异(即被视作替换的差异)。参考图8.17,在时间段T中,序列间的多态性由祖先物种中主导多态性的群体过程引起。随后,在时间段t中,替换是物种间分化过程的产物。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/a99e06a2056e0b9ecd6ea8da56d685ab0d957ccd223e8113495f30d1e024e2ec.jpg]]<br />
| |
| '''图8.21''' 对两个现生物种中采样的DNA序列历史的示意图,用于估计替换率。其历史类似倒置的Y形水管。顶部的管道包含祖先物种中所有谱系的总群体,最终分裂为构成两个物种的谱系群体。两个谱系从共同祖先分化的时间不一定与物种形成的时间相同。因此,在祖先物种中,主导多态性的群体过程运行了<math display="inline">T</math>代,而在分化物种中,分化过程运行了<math display="inline">t</math>代。多态性过程最初决定了两个序列间的核苷酸变化数量,随后分化过程决定了序列间的核苷酸变化数量。在现生种中采样的两个DNA序列中,无法区分观察到的核苷酸变化是由哪个过程引起的。
| |
|
| |
| 祖先多态性与分化过程的存在使分子钟过度离散的检验复杂化(Gillespie 1989, 1994)。为了阐明这一点,Gillespie明确区分了'''起源过程'''(origination processes)与'''固定过程'''(fixation processes)。起源过程描述了最终将被固定的新突变子集首次进入种群的时间。相比之下,固定过程描述了最终将被固定的新突变子集在种群中达到频率1的时间。在概念层面上,这两个过程显然不同。起源时间的分布是突变原因的产物,而固定所需时间既依赖于突变原因(起源过程),也依赖于固定原因——例如有限种群中中性等位基因的遗传漂变或自然选择。
| |
|
| |
| 测量新突变固定所需时间,要求我们能够长期追踪分化物种的种群动态,观察新突变的分离、最终固定或丢失,并记录固定事件的时间作为替代时间。在图8.2中,起源事件是y轴底端的事件,而固定事件是y轴顶端的事件。实践中,我们仅能观察到物种对在某一时间点积累的氨基酸或DNA差异。这类序列差异是起源过程的产物,因为它们是对过去进入种群并已固定的突变的抽样。这与长期观察固定事件的”滴答”过程并不相同。
| |
|
| |
| Gillespie与Langley(1979)证明,结合多态性与分化过程的分子钟不必然构成离散指数等于1的泊松过程。要理解这一点,需要推导当多态性与分化过程共同作用于两条DNA序列的历史时,两序列间核苷酸差异数的期望均值与方差。
| |
|
| |
| 如本章先前对无限位点突变模型的推导,两个DNA序列样本(即<math display="inline">a_{1}=1</math>)的分离位点期望数(S)为θ。这是对有限种群中中性条件下预期多态性水平的预测。该结果表明,在图8.17的祖先多态性区,两个DNA序列样本的核苷酸位点数的均值与方差预期存在差异。
| |
|
| |
| 表8.3 中性位点替代数的均值与方差:两物种分化情形与单一随机交配种群内多态性情形的对比。分化速率建模为泊松过程,故均值等于方差。突变速率为μ,θ=4N_eμ。分化与祖先多态性示意图见图8.17。
| |
|
| |
| {|
| |
| !
| |
| ! 期望均值
| |
| ! 方差
| |
| |-
| |
| | 祖先多态性
| |
| | 0+θ/2
| |
| | θ/2
| |
| |-
| |
| | 分化过程(2μt)
| |
| | 2μt
| |
| | 2μt
| |
| |-
| |
| | 总和(2μt + θ)
| |
| | 2μt + θ
| |
| | 2μt + θ²/2
| |
| |}
| |
|
| |
| 现在将注意力转向图8.17的分歧区。对于来自物种1和物种2的两个DNA序列,分歧时间为2t,因为每个物种都独立演化了t代。基于公式8.38的泊松过程,分化位点的期望数量和分化位点数量的方差都是<math display="inline">2\upmu t</math>。核苷酸位点数量的均值和方差在表8.3中展示,适用于图8.17的多态性和分歧过程。
| |
|
| |
| 给定多态性和分歧过程中两个DNA序列间变化数量的均值和方差,我们可以将这些期望组合成一个新的离散指数表达式。物种1序列和物种2序列间差异数量的离散指数为:
| |
|
| |
| <math display="block">
| |
| R(t)={\frac{\mathrm{Var}N(t)}{E[N(t)]}}={\frac{2\mu t+\theta+\theta^{2}}{2\mu t+\theta}}
| |
| </math>
| |
|
| |
| 其中<math display="inline">\uptheta=4N_{\mathrm{e}}\upmu</math>。(这需要假设谱系分歧时间<math display="inline">T</math>是符合谱系分支模型中几何分布的随机变量,且<math display="inline">N_{e}</math>较大而<math display="inline">\upmu</math>较小。)如数学框8.1所示,这个新版本的离散指数可以重写为:
| |
|
| |
| <math display="block">
| |
| R(t)=1+\frac{\theta^{2}}{E[N(t)]}
| |
| </math>
| |
|
| |
| 如果我们假设没有祖先多态性,或图8.17中<math display="inline">T=0</math>,则θ为0,且<math display="inline">R(t)</math>与仅由分歧决定的泊松过程分子钟预期结果一致。
| |
|
| |
| 主要结论是:当存在祖先多态性时,即使DNA变化遵循恒定分子钟,两过程版本的<math display="inline">R(t)</math>也预期大于1。换句话说,祖先多态性增加了替换次数的方差。
| |
|
| |
| <span id="数学框8.1-含祖先多态性和分歧的离散指数"></span>
| |
| = 数学框8.1 含祖先多态性和分歧的离散指数 =
| |
|
| |
| 定义新变量<math display="inline">\alpha=\frac{t}{2N_{e}}</math>以将时间按<math display="inline">2N_{e}</math>代缩放。注意到:
| |
|
| |
| <math display="block">
| |
| \theta\alpha=4N_{e}\mu\frac{t}{2N_{e}}=2\mu t
| |
| </math>
| |
|
| |
| 将离散指数的分子和分母:
| |
|
| |
| <math display="block">
| |
| R(t)={\frac{2\mu t+\theta+\theta^{2}}{2\mu t+\theta}}
| |
| </math>
| |
|
| |
| 重写为<math display="inline">\upalpha</math>的函数:
| |
|
| |
| <math display="block">
| |
| R(t)=\frac{\theta(1+\alpha)+\theta^{2}}{\theta(1+\alpha)}
| |
| </math>
| |
|
| |
| 并重新整理为:
| |
|
| |
| <math display="block">
| |
| R(t)=\frac{\theta(1+\alpha)}{\theta(1+\alpha)}+\frac{\theta^{2}}{\theta(1+\alpha)}
| |
| </math>
| |
|
| |
| 时间<math display="inline">t</math>时DNA变化的期望数量为<math display="inline">2\mu t+\theta</math>(见表8.3),等价于<math display="inline">\theta(1+\alpha)</math>。离散指数可表示为:
| |
|
| |
| <math display="block">
| |
| R(t)=1+\frac{\theta^{2}}{\theta(1+\alpha)}=1+\frac{\theta^{2}}{E[N(t)]}
| |
| </math>
| |
|
| |
| 在恒定速率下演化的序列对相比纯分歧过程所观察到的情况。遗憾的是,方程8.42中的离散指数【index of dispersion】在实践中似乎无法估计,因为祖先物种中的θ无法估计——该物种已不复存在。然而,这个模型的主要目的并非提供分子钟的实用性检验,而是表明<math display="inline">R(t)>1</math>并不必然是拒绝替代恒定速率的强证据。导致<math display="inline">R(t)>1</math>的一个原因是:泊松过程能准确描述替代过程,但替代速率本身并不恒定。另一种可能性是,即使DNA变化的速率恒定,分歧模型的泊松过程本身可能并不准确。后一种可能性表明,离散指数可能是检验中性分子钟假说的拙劣方法。
| |
|
| |
| 祖先多态性也为利用分子钟测定分歧时间带来了困难(Maddison 1997; Arbogast et al. 2002)。该问题的根源在于序列谱系历史(genealogy)与物种分歧历史(物种系统发育)并不等同。当前从两个不同物种中采样的两条序列,自两条序列的MRCA产生谱系以来一直在积累替代(图8.17)。用于测定物种形成事件时间的两个物种间总序列分歧包含两个不同时间区间的累积。第一个时间区间<math display="inline">T</math>是两条谱系在祖先物种中积累变化的时期。第二个时间区间<math display="inline">t</math>是当前物种分裂后替代继续积累的时期。对分歧时间的估计实际度量的是两条谱系自分歧以来的总历时,而不仅是两个物种的分歧时间。因此,使用分子钟测定分歧时间会导致物种分歧时间的高估。随着分歧时间<math display="inline">t</math>相对于多态性时间<math display="inline">T</math>的增加,高估程度会缩小。然而,实践中通常无法确定<math display="inline">t</math>与<math display="inline">T</math>的相对比例,因此物种分歧时间的高估程度通常未知。
| |
|
| |
| ==== 分子钟的相对速率检验 ====
| |
|
| |
| 一种规避比较绝对分歧速率固有局限性的方法是转而比较相对速率。'''相对速率检验(relative rate test)'''通过比较自共同祖先(以近缘物种的DNA序列为代表)分歧以来的核苷酸或氨基酸变化数量来进行分析(Sarich and Wilson 1967; Fitch 1976)。通过使用第三个外群物种将序列变化分配到各个支系,可以估计两个不同物种中独立发生的DNA或氨基酸变化数量,从而推算核苷酸替换速率。若两个物种的替换速率相等,则在统计学置信区间内两者的序列变化数量应相等。序列变化数量的不等会导致'''零假设(null hypothesis)'''——即两物种具有相同替换速率——被拒绝。相对速率检验避免了常不精确的分歧时间需求,也不依赖离散指数及其隐含的分子钟为简单泊松过程的假设。
| |
|
| |
| Tajima(1993a)提出的分子钟'''一维检验(1D test)'''是一种相对速率检验,它利用被比较的两个支系以及一个外群支系上发生的核苷酸替换数量。该检验的基础如图8.22所示。图中字母i、j和<math display="inline">k</math>代表三个序列在相同核苷酸位点的碱基状态。外群用于确定核苷酸变化发生的时间点——若未发生替换,支系1和2应通过遗传同一性(identity by descent)与外群共享相同碱基对。只有能明确分配到某一支系的变化才适用于比较支系1和2的速率。iji模式的核苷酸替换表明变化发生在支系2,而ijj模式则表明变化发生在支系1。这两种情形允许将替换明确分配到支系以估计替换数量。其他三种可能的核苷酸模式不能用于估计单一支系的替换速率:iii模式的位点因无变化发生而不含速率信息;jji模式的位点中<math display="inline">j</math>的替换可能发生在支系1和2的共同祖先,或两个支系均发生替换但具体事件不明确;ijk模式的位点显示无两分支共享相同核苷酸,故无法判断替换发生时间点,亦不能用于估计支系1和2的替换速率。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/a3e5d1393ae3f5b001af33b756fba116228a43eb5f3f7f71eae9014ac119a8a9.jpg]]
| |
|
| |
| Figure 8.22 比较两个谱系和一个外类群的DNA(或氨基酸)序列时可能的核苷酸变化模式。字母<math display="inline">i</math>、<math display="inline">j</math>和<math display="inline">k</math>用于表示三个序列在同一核苷酸位点的核苷酸类型。例如,iij表示前两个谱系具有相同的碱基对,而第三个谱系具有不同的碱基对。Tajima的1D相对速率检验利用了可明确分配到某一谱系的替换类型(<math display="inline">iji</math>和<math display="inline">ijj</math>)。若谱系1和谱系的替换速率相同,则<math display="inline">E(n_{iji}) = E(n_{ijj})</math>。对于jji和<math display="inline">ijk</math>模式,替换发生的谱系无法被明确确定。iii模式表示所有三个序列的核苷酸相同,因此无替换事件发生。
| |
|
| |
| 根据分子钟假说,谱系1上发生的替换数应与谱系2上发生的替换数相等。由于谱系1和2的分歧时间相同,若两者的替换速率相同,则每个谱系上观察到的替换数也应相同。因此,序列1中发生在谱系1上的替换数(ijj)应等于序列2中发生在谱系2上的替换数(iji):
| |
|
| |
| <math display="block">
| |
| E\left(n_{ijj}\right)=E\left(n_{jij}\right)
| |
| </math>
| |
|
| |
| 其中<math display="inline">E</math>表示期望值或平均值,<math display="inline">n_{ijj}</math>是谱系1上发生的核苷酸替换总数,<math display="inline">n_{jij}</math>是谱系2上发生的核苷酸替换总数。此期望可通过卡方统计量检验:
| |
|
| |
| <math display="block">
| |
| \chi^{2}=\frac{\left(n_{ijj}-n_{iji}\right)^{2}}{n_{ijj}+n_{iji}}
| |
| </math>
| |
|
| |
| 该统计量具有1个自由度。若卡方值大于3.84,则表明两个谱系间的替换数差异不太可能由偶然因素导致。换言之,较大的卡方值可作为拒绝分子钟假说(即两谱系替换速率相等)的证据,并支持速率异质性假设。当<math display="inline">n_{ijj}</math>和<math display="inline">n_{jij}</math>均≥6时,卡方近似是准确的。
| |
|
| |
| Tajima的1D检验无需明确的核苷酸替换模型即可检验两个分类群的分歧速率是否相等,因此操作简便。Hamilton等(2003)利用这一特性,通过核苷酸和插入/缺失(indel)变异比较了巴西坚果树物种间的分歧速率。(由于indel的形成涉及多种分子机制,目前缺乏通用的indel序列变化模型,许多相对速率检验无法用于indel变异。)使用1D检验比较8个物种的替换速率时,他们发现两个树种在核苷酸和indel变化上均不支持分子钟假说。其中一个物种(''Lecythis zabucajo'')的替换速率加速,而另一物种(''Eschweilera romeucardosoi'')的替换速率减缓。
| |
|
| |
| 相对速率检验无法提供外类群分类单元中分子演化速率的信息,也不提供DNA序列变化的绝对速率信息。相对速率检验的结果高度依赖于所使用的外类群(Bromham et al. 2000)。随着两个分类单元共同祖先与外类群分歧时间的增加,所平均的演化速率的时间跨度也随之增加。如果速率异质性是一种短期或近期现象,那么使用远缘外类群进行平均可能会掩盖这种异质性。反之,若速率异质性仅在长时间尺度上显现,使用近期分歧的外类群可能使替代速率显得均质化。最后,由于自然选择依赖于种群特定的适合度值,一般认为在选择同时作用于相对速率检验的两个谱系时,导致速率均质化的可能性很低。
| |
|
| |
| Gu和Li(1992)以及Muse和Weir(1992)描述了结合核苷酸替代模型并使用最大似然框架的三分类单元相对速率检验。此外,还有多种利用系统发育树的相对速率检验方法,可同时使用多个分类单元的序列来检验分子钟假说(参见Nei和Kumar 2000;Page和Holmes 1998)。
| |
|
| |
| ==== 速率异质性的模式与成因 ====
| |
|
| |
| 大田和木村(1971)首次通过严格的统计比较方法对泊松过程的分子钟进行了检验。他们使用了来自多个物种的三个基因座(β珠蛋白、α珠蛋白和细胞色素c)的蛋白质序列。基于观察到的序列对间分歧度以及物种分歧时间估计,他们计算了一系列绝对分歧速率。这些绝对速率差异显著(其数据的离散指数介于1.37至2.05),导致他们拒绝了恒定分子钟的假说(见Gillespie 1991)。数年后,Langley和Fitch(1974)对相同三个基因座及纤维蛋白肽A的绝对替代速率进行了更大规模分析,并利用系统发育树更好地估计了各物种的替代数。他们也发现所有基因座的离散指数均大于1。这些研究引起了广泛关注,因为序列变化速率的差异需要得到解释。自这些早期研究以来,大量关于分子演化绝对速率和相对速率的数据清楚地表明,分子演化速率通常比泊松过程模型预期的更具变异性。事实上,速率异质性现已被视为常态,而恒定分子演化速率反而成为例外。本节重点讨论解释分子演化速率变异的假说。
| |
|
| |
| 在中性理论下,不同位点间分化速率的变异可以通过突变率的差异来解释。类似地,同一基因座在不同物种中的分化速率差异也可归因于物种间不同的突变率。这种同一基因座在不同物种中分子进化速率的变异被称为分子钟的谱系效应(Gillespie 1989, 1991;参见 Carruthers 等 2019)。即使在考虑谱系间变异后,某个基因座仍可能表现出明显的速率异质性,这被称为残留效应。残留效应是指随时间推移,谱系内分化速率的变异或分子钟”滴答”速率的不均匀性(见图 8.16)。残留效应有时被描述为替换以突发或集群方式发生,中间间隔无变化的模式。另一种理解方式是:某些谱系中特定基因座的替换速率差异,或谱系与基因座的交互方差。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/e6f8d90235d4718d9ac84f044d11516c1b706d0a2b64a42b356e5f03f729424c.jpg]]<br />
| |
| 图 8.23 替换速率变异的三种类型,分别对应不同机制。基因座间替换速率变异(A)可通过中性理论解释为不同基因座的突变率差异。谱系间替换速率变异(B)可由谱系内所有基因座共有的机制解释,例如整体更快的突变率或世代时间效应。基因座与谱系交互作用变异(C)或残留变异,可通过自然选择解释——不同谱系中基因座经历的选择压力不同。这三种替换速率变异类型并非互斥。
| |
|
| |
| '''谱系效应''':多个物种间分化速率的变异,可解释为不同谱系具有可变的中性突变率。<br />
| |
| '''非复制依赖的突变诱因''':可能随时发生的突变原因,因此与细胞分裂速率无关。例如环境诱变剂如紫外线辐射、γ粒子和化学物质。
| |
|
| |
| '''残留效应''':谱系内无法通过谱系间或基因座间速率异质性解释的分化速率变异或不均匀性。
| |
|
| |
| Kimura(1983)认为不同物种的突变率以年为单位大致恒定。如果引起突变的进程在年等时间单位内保持恒定,这一观点可能成立。例如非复制依赖的突变诱因——如紫外线辐射、<math display="inline">\upgamma</math>粒子或化学诱变剂的暴露。细胞内持续产生的自由基离子是另一个非复制依赖的突变诱因案例。这些外源性突变诱因的暴露量在日历时间上保持恒定似乎是合理的,因此由非复制依赖诱因产生的部分突变率也以日历时间为基准。
| |
|
| |
| 回到中性理论的基础,可以解释为何不同物种可能不会以相同的速率经历替代。如本章开头所示,中性理论预测替代速率等于突变速率。但由于突变速率是以每代的核苷酸变化来衡量的,因此替代速率也以每代为时间单位表达。这导致了一个问题:如果物种的世代时间不同,恒定的分子钟可能不存在。例如,假设两个物种具有相同的突变速率,即每代每碱基对<math display="inline">\upmu=1\times{10}^{-5}</math>次错误。现在假设这两个物种的世代时间分别为10年和100年。世代时间较短的物种具有:
| |
|
| |
| <math display="block">
| |
| \begin{array}{c}{{\mu=\displaystyle\frac{1\times10^{-5}\mathrm{mutations~generation^{-1}~}}{10\mathrm{years~generation^{-1}~}}}}\ {{=1\times10^{-6}\mathrm{mutations\mathrm{per}\mathrm{year}}}}\end{array}
| |
| </math>
| |
|
| |
| 而世代时间较长的物种具有:
| |
|
| |
| <math display="block">
| |
| \begin{array}{c}{{\mu=\frac{1\times10^{-5}\mathrm{mutations~generation}^{-1}}{100\mathrm{years~generation}^{-1}}}\ {{=1\times10^{-7}\mathrm{mutations~per~year}}}\end{array}
| |
| </math>
| |
|
| |
| 因此,当中性理论预测的每代恒定分子钟被用于比较具有不同世代时间的物种时,每年观察到的替代速率可能会发生变化。
| |
|
| |
| 中性突变速率在每代恒定的情况下,每年观察到的速率可能发生变化的这一现象,引出了'''世代时间假说'''——该中性理论解释认为,替代速率的差异源于具有每代恒定替代速率的物种间世代时间的差异。大量研究已为替代速率的世代时间效应提供了证据(Li et al. 1987, 1996; Ohta 1993, 1995)。表8.4展示了不同哺乳动物类群中多个核基因观测到的替代速率。
| |
|
| |
| 啮齿类(rodents)的世代时间短于灵长类(primates)和偶蹄类(artiodactyls)。替代速率与世代时间呈负相关。相比之下,同类群内的比较(如小鼠与大鼠的替代速率比较)显示替代速率几乎相等。啮齿类相较于灵长类和偶蹄类表现出加速的替代速率,这是世代时间效应的经典案例,与分子进化速率异质性的中性解释一致。
| |
|
| |
| '''表8.4''' 不同哺乳动物目在49个核基因中观测到的每核苷酸位点替代数。分歧被划分为同义位点与非同义位点。灵长类和偶蹄类(具偶数趾的有蹄哺乳动物,如牛、鹿和猪)的世代时间长于啮齿类。同义位点总数为16 747,非同义位点总数为40 212。
| |
|
| |
| {|
| |
| ! Mammal group
| |
| ! Synonymous sites
| |
| ! Nonsynonymous sites
| |
| |-
| |
| | Primates
| |
| | 0.137
| |
| | 0.037
| |
| |-
| |
| | Artiodactyls
| |
| | 0.184
| |
| | 0.047
| |
| |-
| |
| | Rodents
| |
| | 0.355
| |
| | 0.062
| |
| |}
| |
|
| |
| 数据来源:Ohta (1995)。
| |
|
| |
| '''世代时间假说''':<br />
| |
| 认为替代速率的变异源于具有每代恒定替代速率的物种间世代时间差异的假说。
| |
|
| |
| = 分子进化速率的异质性 =
| |
|
| |
| 这种对速率异质性的解释与中性分子进化理论一致。
| |
|
| |
| '''复制依赖性突变原因''':在DNA复制过程中发生的突变原因,例如复制错误,因此突变速率取决于细胞分裂速率。
| |
|
| |
| '''世代时间效应'''可通过复制依赖性突变原因解释。如果突变主要发生在染色体复制的细胞分裂过程中,那么每代更多的细胞复制将导致每代中性分歧速率升高。在动物中,每代复制依赖性突变速率的差异可能由导致生殖系细胞(产生配子的细胞)的固定细胞分裂次数解释。这解释了雄性配子中突变发生率高于雌性配子的观察结果,因为雄性生殖系细胞分裂次数多于雌性。若世代时间与生殖系细胞分裂次数相关(例如,世代时间较长的动物具有更多生殖系细胞分裂),则动物的世代时间效应可由此解释。然而,研究表明,首次开花时间间隔较短的植物具有更高的替换速率(Gaut 1998; Kay et al. 2006)。植物分子进化速率的变异表明,生殖系细胞分裂并非速率异质性的唯一解释,因为植物不具有独立的生殖细胞与体细胞系。
| |
|
| |
| Martin和Palumbi(1993;由Rand 1994评述)提出的'''代谢率假说'''基于以下观察:尽管所有研究的分类群具有相对相似的世代时间,但鲨鱼的同义替换速率比灵长类和偶蹄类低5至7倍。突变速率可能与生物体的代谢率相关,原因包括:高代谢率生物体的细胞功能运作快速,其中一项功能是DNA复制。因此,高代谢率导致高DNA复制速率和高复制依赖性突变速率。另一种机制是,细胞内的有氧呼吸产生游离氧自由基,引起DNA的氧化损伤。因此,高代谢率增加了暴露于诱变剂的速率,并提高了非复制依赖性突变速率。这两种将代谢率与突变速率关联的机制并非互斥,可同时发生。Gillooly等(2005)提出了一个明确包含体型和温度效应的替换速率模型,并提出在考虑这些因素引起的速率变异后,分子钟可能确实保持恒定。
| |
|
| |
| 分歧速率的异质性也可以用近中性理论来解释(Ohta 1992综述)。为了理解这一点,令<math display="inline">\mathrm{f_{0}}</math>表示因负选择压力相对于有效种群大小较弱而被视为选择性中性的突变比例(所有突变都被假定为有害突变,而有利突变因过于罕见可被忽略——这是近中性理论中一个有争议的假设,见Gillespie 1995)。剩余部分<math display="inline">(1-\mathsf{f}_{0})</math>的突变具有足够大的有害效应,会受到负选择作用而非中性。根据近中性理论,中性突变的替代速率为:
| |
|
| |
| <math display="block">
| |
| k=f_{0}\mu
| |
| </math>
| |
|
| |
| 这与中性理论的公式8.3类似。该方程表明,当更多突变实际表现为中性时(<math display="inline">\mathrm{f_{0}}</math>较大),分歧速率会更高;当更少突变实际表现为中性时(<math display="inline">\mathrm{f_{0}}</math>较小),分歧速率会更低。
| |
|
| |
| 由于实际表现为中性的突变比例取决于有效种群大小,根据近中性理论,分歧速率也会随有效种群大小的变化而变化。在近中性理论中,所有替代都是遗传漂变的结果(与中性理论一致)。但更大的有效种群大小会导致更少的突变实际表现为中性,从而减少最终能到达固定状态的中性突变库。相反,更小的有效种群大小会导致更多突变实际表现为中性,从而扩大最终可能发生替代的中性突变库。因此,近中性理论预测分歧速率与有效种群大小呈负相关,因为<math display="inline">N_{e}</math>的变化会引起<math display="inline">\mathrm{f_{0}}</math>的变化。根据近中性理论,速率异质性可以通过不同谱系或基因座的有效种群大小差异导致<math display="inline">\mathrm{f_{0}}</math>变化来解释。
| |
|
| |
| 世代时间也可能影响近中性理论下物种间替换率变异的感知。在近中性理论中,如同中性理论一样,突变率和替换率都以每世代为单位表示。这应该会导致世代时间对替换率产生影响,正如中性理论中的情况。然而,在近中性理论中,由于世代时间与有效种群大小之间的负相关关系,世代时间效应可能会被抵消。在近中性理论中,有效中性突变的比例取决于有效种群大小。
| |
|
| |
| 独立地,若每世代的突变率恒定,更长的世代时间会导致每年发生的替换更少,而更短的世代时间则会导致每年发生更多替换。有效种群大小和世代时间应该对替换率产生独立影响。然而,实际上世代时间与有效种群大小通常并不独立(Chao 和 <math display="inline">\mathrm{Carr1993}</math>)。例如,鼠类具有短世代时间和大的有效种群大小,而象类具有长世代时间和小的有效种群大小。因此,世代时间和有效种群大小的影响往往会相互抵消,导致近中性理论预测替换率不会表现出世代时间效应。
| |
|
| |
| <span id="检验dna序列多态性的中性理论零模型"></span>
| |
| ==== 8.6 检验DNA序列多态性的中性理论零模型 ====
| |
|
| |
| '''Hudson-Kreitman-Aguadé(HKA)检验'''。'''McDonald-Kreitman(MK)检验'''。<br />
| |
| '''错配分布(Mismatch distributions)'''。<br />
| |
| '''Tajima’s D'''
| |
|
| |
| 本节提供了应用本章先前发展的中性理论概念性结果来检验分子进化成因的中性零模型的机会。部分检验利用了中性理论对多态性水平与分歧度的预测,而另一些则依赖于早前章节中发展的溯祖模型结果【“coalescent model”译为“溯祖模型”】。这些检验已被广泛应用于来自众多位点、基因组和物种的DNA序列实证研究中(参见Ford 2002年的综述)。本节描述的检验极大地增进了我们对自然选择如何作用于DNA序列的理解,也加深了我们对自然种群中多种群体遗传过程(交配、基因流、遗传漂变、突变、<math display="inline">N_e</math>变化以及自然选择)相互作用机制的认识。
| |
|
| |
| ==== 检验近中性理论关于世代时间与有效种群大小相互抵消效应的预测 ====
| |
|
| |
| 可以通过实验验证近中性理论的预测——世代时间与有效种群大小对分子进化速率的效应往往会相互抵消。Ohta(1995)通过比较灵长类、偶蹄类和啮齿类49个基因的同义与非同义位点替换速率进行了此类检验(本节前文提及,这些动物的分歧速率支持世代时间假说)。Ohta将外显子中的DNA序列数据划分为同义或非同义位点观察到的分歧。非同义位点的突变会受到自然选择的作用,因为它们会改变蛋白质的氨基酸序列从而产生表型效应。相反,同义位点突变由于不改变氨基酸序列,不被自然选择感知(或选择作用微弱)。
| |
|
| |
| 近中性理论预测,由于对非同义突变库的负向选择(非同义突变率<math display="inline">\mathrm{f_{0}}</math>较小),非同义替换速率应低于同义替换速率。此外,对于近中性突变而言,由于世代时间与有效种群大小呈负相关,非同义位点的分歧速率不应表现出世代时间效应。表8.4显示了Ohta关于灵长类、偶蹄类和啮齿类同义与非同义位点的分歧数据。正如非同义位点经历频繁负向选择的预期,同义替换速率比非同义替换速率高一个数量级。啮齿类的同义替换速率是灵长类的2.59倍,而非同义替换速率仅为灵长类的1.68倍。因此,非同义位点的分歧表现出较弱的世代时间效应,这也与近中性理论一致。
| |
|
| |
| <span id="hka检验中性理论对dna序列进化预期的验证"></span>
| |
| ==== HKA检验:中性理论对DNA序列进化预期的验证 ====
| |
|
| |
| HKA 检验,以其作者 Hudson、Kreitman 和 Aguadé(Hudson et al. 1987)命名,是一种将中性理论对 DNA 序列演化的预测与经验估计的多态性及分化进行比较的检验方法。该检验基于中性条件下物种内多态性与物种间分化都是突变率产物的理论预期。事实上,在中性演化下,某基因座的多态性水平与分化水平应存在相关性,因为它们都是相同突变事件的产物。例如,若某基因座具有高突变率,则群体应表现出高度多态性(见公式 8.1)。同时,该基因座与其他物种比较时的分化水平也应较高,因为导致分化的替换速率同样等于突变率(见公式 8.2 和 8.3)。反之,若中性基因座具有低突变率,则应同时表现出低多态性与低分化水平。由此可知,在中性条件下,多态性与分化水平的预期值并非相互独立。若分化与多态性缺乏相关性,则与中性预期相悖,从而为拒绝所研究基因座的中性零模型提供证据。
| |
|
| |
| HKA 检验需要两个基因座的 DNA 序列数据。其中一个基因座作为选择性中性的参考或对照基因座,通常选择非编码基因组区域或无功能的基因重复拷贝(假基因),这两类区域预期相对不受核苷酸替换的功能限制。另一个基因座则是检验的焦点,即待验证中性演化零模型的基因座。
| |
|
| |
| HKA 检验还要求以特定方式收集两个基因座的 DNA 序列数据。首先,必须从两个物种获取两个基因座(中性参考基因座与待测基因座)的 DNA 序列,以估计物种间的分化水平。此外,需获取其中一个物种内多个个体的 DNA 序列,用于估计两个基因座的多态性水平。多态性通过各基因座的核苷酸多样性(π)衡量,分化则通过比较两个物种个体间基因座的 DNA 序列,并采用核苷酸替换模型校正同塑性【homoplasy】进行估计。
| |
|
| |
| 一旦从DNA序列数据中获得多态性和分歧度的估计值,它们就可以以表8.5所示的格式进行比较。表8.5a展示了中性理论对两个基因座多态性和分歧度的预期。在无限位点模型的中性假设下,DNA序列多态性预期为<math display="inline">\uptheta=4N_{e}\upmu</math>,而分歧度预期为<math display="inline">k=2T\mu</math>。测试基因座和参考基因座可能具有不同的突变率。但需注意,当从同一物种中取样估计两个基因座的多态性时,有效种群大小是恒定的。两个基因座的分歧时间也相等,因为它们来自同一物种对的估计。
| |
|
| |
| 测试基因座与参考基因座的分歧度估计值之比,预期等于两个基因座突变率之比<math display="inline">(\frac{\mu_{T}}{\mu_{R}})</math>,因为<math display="inline">4N_{e}</math>因子会被抵消。测试基因座与参考基因座的分歧度估计值之比也预期等于<math display="inline">\frac{\mu_{T}}{\mu_{R}}</math>。因此,在中性条件下,两个基因座的多态性估计值之比以及分歧度估计值之比应当相等,因为它们都代表两个基因座突变率的比值。类似地,每个基因座的多态性与分歧度之比在中性条件下也应相等。这些比值的相等性可通过卡方检验进行验证。
| |
|
| |
| 表8.5b展示了符合DNA序列演化中性零假设的多态性与分歧度估计的理想化示例。在此理想化情境中,两个基因座确实具有不同的突变率,导致不同水平的多态性和分歧度。然而,若突变命运仅由遗传漂变决定,这些比值将如预期般相等。
| |
|
| |
| 表8.5c展示了果蝇中用于实施HKA检验(Hudson et al. 1987)的分歧度与多态性估计的经典案例。被测试中性演化的基因座是乙醇脱氢酶基因<math display="inline">(A d h)</math>,参考基因座是编码区上游<math display="inline">(5^{\prime})</math>不具开放阅读框的序列。通过<math display="inline">D</math>. melanogaster个体的样本估计了两个基因的多态性,并通过_Drosophila sechellia_的序列确定了两个基因座的分歧度。若<math display="inline">5^{\prime}</math>侧翼区域确为中性,则_Adh_数据显示了<math display="inline">D</math>. melanogaster内过多的多态性。_Adh_多态性的超额还体现在_D. melanogaster_内两个基因座多态性比值与两个基因座分歧度比值的显著差异上。目前学界普遍认为,_D. melanogaster_的_Adh_基因座表现出符合平衡选择的多态性超额。
| |
|
| |
| 表 8.5 基于HKA检验的两个物种中两个基因座的多态性与分歧度估计。中性条件下多态性与分歧度的相关性导致基因座间的分歧度与多态性之比独立于其突变率而保持恒定,同时基因座间的多态性或分歧度之比也保持恒定(A)。案例B展示了符合中性零模型的理想多态性与分歧度估计示例。案例C中果蝇''Adh''基因及侧翼区域的数据(Hudson等,1987)与中性进化模型不一致,因为黑腹果蝇''Drosophila melanogaster''内''Adh''多态性水平相较于其与塞氏果蝇''D. sechellia''间侧翼区域的分歧度高于预期。
| |
|
| |
| {|
| |
| !width="28%"| A.中性案例预期
| |
| !width="20%"|
| |
| !width="23%"|
| |
| !width="27%"|
| |
| |-
| |
| |
| |
| | 检验基因座
| |
| | 中性参考基因座
| |
| | 比值(检验/参考)4NeμT = μ
| |
| |-
| |
| | 焦点物种多态性(π)
| |
| | 4N<sub>e</sub>μ<sub>T</sub>
| |
| | 4N<sub>e</sub>μ<sub>R</sub>
| |
| | 4N<sub>e</sub>μ<sub>T</sub> / 4N<sub>e</sub>μ<sub>R</sub> = μ<sub>T</sub>/μ<sub>R</sub>
| |
| |-
| |
| | 种间分歧度(K)
| |
| | 2Tμ<sub>T</sub>
| |
| | 2Tμ<sub>R</sub>
| |
| | 2Tμ<sub>T</sub> / 2Tμ<sub>R</sub> = μ<sub>T</sub>/μ<sub>R</sub>
| |
| |-
| |
| | 比值(π/K)
| |
| | 4N<sub>e</sub>/2T
| |
| | 4N<sub>e</sub>/2T
| |
| |
| |
| |}
| |
|
| |
| {|
| |
| !width="28%"| B.中性案例示例
| |
| !width="20%"|
| |
| !width="23%"|
| |
| !width="27%"|
| |
| |-
| |
| |
| |
| | 检验基因座
| |
| | 中性参考基因座
| |
| | 比值(检验/参考)
| |
| |-
| |
| | 焦点物种多态性(π)
| |
| | 0.10
| |
| | 0.25
| |
| | 0.40
| |
| |-
| |
| | 种间分歧度(K)
| |
| | 0.05
| |
| | 0.125
| |
| | 0.40
| |
| |-
| |
| | 比值(π/K)
| |
| | 2.0
| |
| | 2.0
| |
| |
| |
| |}
| |
|
| |
| {|
| |
| !width="29%"| C.黑腹果蝇与塞氏果蝇的实证数据
| |
| !width="17%"|
| |
| !width="28%"|
| |
| !width="24%"|
| |
| |-
| |
| |
| |
| | ''Adh'' 0.101
| |
| | 5′ ''Adh''侧翼区域
| |
| | 比值(''Adh''/侧翼)
| |
| |-
| |
| | ''D. melanogaster''多态性(π)
| |
| |
| |
| | 0.022
| |
| | 4.59
| |
| |-
| |
| | 种间分歧度(K)
| |
| | 0.056
| |
| | 0.052
| |
| | 1.08
| |
| |-
| |
| | 比值(π/K)
| |
| | 1.80
| |
| | 0.42
| |
| |
| |
| |}
| |
|
| |
| 尽管HKA检验设计巧妙,但仍存在一些局限性和假设。实际应用中的一个难点是确定明确中性的参考基因座。例如,Hudson等(1987)用作中性参考基因座的5′侧翼区域很可能包含受自然选择功能约束的启动子序列【“promoter sequences”译为“启动子序列”】。Innan(2006)提出了一种改进方法,使用多个参考基因座的平均值进行HKA检验。
| |
|
| |
| HKA检验隐含的假设是所使用的两个物种均为随机交配群体。种群结构有可能改变核苷酸多态性和分化水平及其模式(参见Charlesworth等2003年的综述),具体取决于个体的采样方式。考虑一个<math display="inline">F_{ST}</math>大于0的结构化物种中的多态性水平:种群结构会导致亚种群内采样的个体多态性降低,这既由于有效种群规模减小导致亚群内漂变增强,也由于亚群内交配概率增加导致自合性(autozygosity)升高。相反,从两个不同亚群采样的个体间遗传差异会更大,这是由于亚群间分化导致观测到高水平的多态性。如果对具有种群结构的物种进行HKA检验,采样时需要避免仅从一个或少数几个局域种群中获取序列,否则可能得出”与中性预期相比多态性过低”的错误结论。Ingvarsson(2004)展示了当存在种群结构时,HKA检验如何导致错误拒绝中性零假设。该论文还提供了一个经过种群结构校正的HKA检验案例,应用于具有强烈种群结构的植物物种''Silene vulgaris''和''Silene latifolia''的细胞器DNA序列数据。
| |
|
| |
| <span id="mcdonald-kreitmanmk检验"></span>
| |
| ==== McDonald Kreitman(MK)检验 ====
| |
|
| |
| MK检验是对两个物种间DNA序列分化的中性模型的检验(McDonald和Kreitman 1991)。与HKA检验类似,它以作者McDonald和Kreitman命名。MK检验在概念上也与HKA检验相似,因为它同样基于中性条件下单个位点的两类DNA变化的预期比值。MK检验需要单个编码基因的DNA序列数据:从焦点物种的多个个体采集DNA序列样本以估计多态性,同时需要另一物种同一位点的DNA序列以估计分化。
| |
|
| |
| 表8.6列出了MK检验的中性预期。MK检验中使用的两类DNA变化是同义和非同义(或替换)变化。编码区内的非同义突变可能改变密码子指定的氨基酸。由于遗传密码的冗余性,编码区内的某些突变不会改变密码子指定的氨基酸,因此属于同义变化。
| |
|
| |
| 如果遗传漂变是影响新突变命运的唯一过程,那么DNA变化每一类别的多态性水平和分化程度应当相关,因为它们都部分由突变速率决定。物种间的固定差异由已固定化的突变引起,中性理论下的预期分化值为<math display="inline">2T\upmu</math>。在焦点物种(''focal species'')内具有两个或多个核苷酸的核苷酸位点表现出多态性,中性理论下的预期水平为<math display="inline">4N_{e}\upmu</math>。由于同义和非同义突变可能以不同速率发生,我们可以为每类DNA变化分配不同的速率(<math display="inline">\upmu_{N}</math>和<math display="inline">\upmu_{S}</math>)。根据中性理论,非同义与同义固定差异的比率,以及非同义与同义多态位点的比率,都应等于<math display="inline">\upmu_{N}/\upmu_{S}</math>。因此,MK检验通过比较这两个比率是否相等来检验中性理论。表8.6b中的中性案例展示了一个例子:当<math display="inline">\upmu_{N}<\upmu_{S}</math>时,多态性水平高于分化水平。尽管如此,如果两类突变均为中性,固定差异和多态位点的非同义变化与同义变化的数量比率将如预期保持恒定。
| |
|
| |
| <pre class="markdown">一个编码位点构成了MK检验的基础。在中性条件下,非同义位点数量除以同义位点数量等于非同义与同义突变率的比值。该比值在物种间存在固定差异的核苷酸位点和目标物种内的多态性位点中应保持恒定(A)。案例B展示了理想状态下非同义与同义位点的示意图。
| |
|
| |
| (McDonald and Kreitman 1991)在C中显示,相比基于趋异预期的结果,果蝇*Adh*基因座的非同义多态性存在过量。人类*Hla-B*基因座数据显示多态性过量且更多。
| |
|
| |
| ### A. 中性情况预期
| |
|
| |
| | | 固定差异 | 多态性位点 |
| |
| |--------------------|-------------------|--------------------|
| |
| | 非同义位点(N) | N<sub>f</sub>=2Tμ<sub>N</sub> | N<sub>p</sub>=4N<sub>e</sub>μ<sub>N</sub> |
| |
| | 同义位点(S) | S<sub>f</sub>=2Tμ<sub>S</sub> | S<sub>p</sub>=4N<sub>e</sub>μ<sub>S</sub> |
| |
| | 比值(N/S) | μ<sub>N</sub>/μ<sub>S</sub> | μ<sub>N</sub>/μ<sub>S</sub> |
| |
|
| |
| ### B. 中性情况示意图
| |
| | | 固定差异 | 多态性位点 |
| |
| |-------------------|----------|------------|
| |
| | 非同义替换数 | 4 | 15 |
| |
| | 同义替换数 | 12 | 45 |
| |
| | 比值 | 0.33 | 0.33 |
| |
|
| |
| ### C. 黑腹果蝇*Adh*基因座实证数据(McDonald and Kreitman 1991)
| |
| | | 固定差异 | 多态性位点 |
| |
| |-------------------|----------|------------|
| |
| | 非同义替换数 | 7 | 2 |
| |
| | 同义替换数 | 17 | 42 |
| |
| | 比值 | 0.412 | 0.048 |
| |
|
| |
| ### D. 人类*Hla-B*基因座实证数据(Garrigan and Hedrick 2003)
| |
| | | 固定差异 | 多态性位点 |
| |
| |-------------------|----------|------------|
| |
| | 非同义替换数 | 0 | 76 |
| |
| | 同义替换数 | 0 | 49 |
| |
| | 比值 | — | 1.61 |
| |
|
| |
| 基于果蝇物种间固定或黑腹果蝇*D. melanogaster*种群内多态性的*Adh*基因座同义与非同义替换数的MK检验见表8.6c(McDonald and Kreitman 1991)。以固定序列差异为参照点,物种间非同义替换数少于同义替换数。非同义替换速率为同义替换速率的41.2%。在中性条件下,我们预期黑腹果蝇*D. melanogaster*约41%的多态性位点位于非同义位点。然而观测数据显示,仅约4.5%的多态性位点为非同义位点。因此,多态性位点的同义替换过多或非同义替换过少,与中性多态性水平不一致。(注意:若以多态性位点为参照框架,则本例中非同义位点的趋异速率相比中性预期有所升高。)```
| |
|
| |
| 在编码DNA序列的研究中,一个常见的观察现象是:非同义DNA改变与同义DNA改变的数量并不相等。对此模式的中性解释是这两种DNA改变具有不同的基础突变率。如果突变随机发生在核苷酸位点上,理论上非同义改变应比同义改变更频繁。事实上,密码子第一位点的核苷酸改变中有96%、第二位点的所有改变以及第三位点改变中的30%属于非同义改变。总体而言,若突变在编码序列中随机发生,则75.3%的突变属于非同义突变,24.7%为同义突变。
| |
|
| |
| 另一种解释认为同义与非同义突变的速率大致相等,但非同义突变常通过破坏蛋白质功能的方式改变其结构。导致功能受损的非同义突变也会降低适合度,因此会受到净化自然选择的作用。此外,某些非同义突变可能增强功能,并通过正选择快速固定。第三种非中性解释是:通过平衡选择作用,非同义突变在群体中以中等频率维持。强平衡选择的典型案例是人类白细胞抗原(*Hla*)B基因——Garrigan和Hedrick(2003)通过人类与黑猩猩的趋异数据(表8.6d)使用MK检验发现该基因的特征。该位点在人类与黑猩猩之间没有固定DNA差异,表明这两个物种分化后该位点的突变率较低。与之形成对比的是,人类群体中该位点显示出高水平的多态性,且非同义改变与同义改变的比例为1.6:1,这与中性假说所预测的多态性与趋异程度相关的结论相矛盾。*Hla*基因构成主要组织相容性复合体(MHC)区域,其编码的细胞表面抗原呈递蛋白在免疫系统功能中起重要作用。这些位点的杂合子具有更高的适合度,因为它们能呈递更多样化的细胞表面抗原。
| |
|
| |
| #### 错配分布
| |
|
| |
| 上一节探讨了如何通过比较基于核苷酸多样性$(\pi)$和分离位点数$(S)$估算的θ值,利用群体DNA序列样本检验中性预期。π和S都将序列变异模式概括为单一数值。具体而言,核苷酸多样性π实际上是样本中所有序列对间差异的平均值。我们可以不采用平均值来衡量多态性,而是直接检查所有成对序列比较的分布。这通常称为错配分布,即样本中所有独特DNA序列对间差异位点数的频率分布。错配分布是推断DNA序列样本群体历史的重要工具,可用于通过中性DNA序列推断群体有效大小的历史变化。对于长期保持恒定大小的群体,该分布还可用于识别自然选择的作用。
| |
|
| |
| **错配分布**:同一物种样本中所有独特DNA序列对间差异位点数的频率分布,亦称成对差异分布。
| |
|
| |
| **单倍型频率分布**:假设个体为单倍体或纯合时,群体中各序列单倍型频率的分布,亦称位点频谱【"site frequency spectrum"译为"位点频谱"】。
| |
|
| |
| 为研究稳定、增长和收缩群体中DNA序列差异模式的预期,我们假设突变完全中性,重点利用错配分布建立理论框架。错配分布的特性直接源于中性基因谱系的预期模式。第3章表明,在恒定$N_{e}$群体的标准中性基因谱系中,最后一对谱系$(k=2)$的平均溯祖时间最长。存在突变时,群体中最古老的两个谱系间也积累了最多突变(因突变数与谱系存在时间成正比)。在维持恒定$N_{e}$的群体中,这两个最古老谱系经历大量突变,因而具有高度错配。图8.24的基因谱系清晰展示了这种长谱系携带多重突变的模式。
| |
|
| |
| 从过去到现在追溯,任何谱系中最古老的两个支系会产生额外的支系。较年轻的子代支系继承了祖先支系上发生的所有突变,也可能经历额外的新突变。由于靠近现在的支系往往具有更短的溯祖时间(随着k增大,溯祖概率增加),它们也倾向于积累更少的突变。观察图8.23,A组内的三个支系各自继承了其祖先内部分支上发生的四个突变。由于A组内的支系1、2和3共享其祖先支系的突变,它们的核苷酸位点错配也往往更少。例如,支系1和2仅因近期发生的两个突变(核苷酸位点17和22的突变)而不同。同理,B组内的支系4、5和6也具有较低的错配水平。
| |
|
| |
| 
| |
| 图8.24 使用核苷酸多样性$(\hat{\theta}_{\pi})$和分离位点数量$(\hat{\theta}_{S})$对比例化突变率θ的估计会因突变在谱系中的位置不同而有所差异。在无限等位模型假设下,无论突变发生在何处,每个突变都会产生单个分离位点。然而,内部分支上的突变会出现在多重成对比较中,导致$\pi$值增大(A)。相比之下,仅引起单个支系核苷酸变化的外部分支突变(B)对$\pi$的贡献较小。计算$\pi$时,A中的每个突变被计数四次$(d_{13},d_{23},d_{14}$和$d_{24})$,而B中的突变被计数三次$(d_{12}$ $\boldsymbol{\cdot},d_{23},d_{24})$。
| |
|
| |
| 相比之下,如图8.24所示,当比较A组和B组之间的支系时,序列错配水平较高。例如,支系1和4存在九个突变的差异。这种高错配水平是因为远缘支系的序列自共享共同祖先支系以来经历了更长的分离时间,导致更多的突变变化独立地改变了每个DNA序列。另一种理解方式是:近缘支系仅因少数近期突变而不同,而远缘支系因更多突变产生差异,其中许多是古老突变并在种群中长期存在。
| |
|
| |
| 不匹配分布(mismatch distribution)的形态因种群的历史群体动态而异(Slatkin 和 Hudson 1991;Rogers 和 Harpending 1992)。在有效种群大小($N_{e}$)长期保持稳定的种群中,不匹配分布通常呈现双峰结构。这种双峰分布是过去有效种群大小相对恒定时谱系结构的特征信号。双峰模式源于所有内部和外部分支的溯祖时间大致相等。相反,历史上经历过有效种群大小快速增长或急剧收缩的种群,其不匹配分布会呈现明显不同的形态。
| |
|
| |
| 在有效种群大小快速增长的种群中(见[“In populations that have rapidly growing $N_{e}$”译为“在有效种群大小快速增长的种群中”]),大多数溯祖事件发生在谱系早期靠近最近共同祖先(MRCA)的位置,因为向现代推移时溯祖概率逐渐降低(见图8.26左)。这导致较长的外部分支各自积累大量独特突变,使得不匹配分布呈现高频的高差异序列对和低频的低差异序列对。反之,在持续经历有效种群大小衰退的种群中,由于向现代推移时溯祖概率逐渐升高(见图8.26右),大多数溯祖事件发生在靠近现代的位置。这类收缩种群的[“mismatch distribution”译为“不匹配分布”]通常表现为高频的低差异序列对。
| |
|
| |
| 另一种分析多态性的相关方法是考察样本中单倍型频率的分布。这种单倍型频率分布展示了种群中各观测序列等位(假设个体为单倍体或纯合体)所占比例。在中性演化且有效种群大小恒定的条件下(见图8.26),预期会观测到从高频到低频的连续单倍型分布。当种群快速增长或存在平衡选择时,谱系外部分支的过度延长将导致稀有单倍型数量异常增多。当种群快速收缩或存在强方向选择时,由于谱系分支长度主要分布在内部支系,预期会出现高频单倍型占优而稀有单倍型极少的分布格局。
| |
|
| |
| #### 错配分布与单倍型频率分布
| |
| 若序列呈中性,错配分布(mismatch distribution)和单倍型频率分布(haplotype frequency distribution)可帮助识别有效种群大小(effective population size)扩张或收缩的实例。反之,若已知序列来自有效大小恒定的种群,则这些分布可用于识别自然选择的作用。现有多种检验方法通过单倍型频率或错配分布,利用DNA序列数据评估"有效种群大小随时间恒定"的零假设(Fu和Li 1993;Fu 1996,1997;Schneider和Excoffier 1999;Mousset等2004;Innan等2005)。需注意这些检验存在若干局限性:
| |
|
| |
| 第一,重组可能影响错配分布并混淆种群统计学信号。重组事件通过将现存单倍型组装为新单倍型,从而打破因共同祖先而关联的突变。因此,重组会模糊突变的历史记录,极端情况下会导致均匀的错配分布。
| |
|
| |
| 第二,溯祖(coalescence)是随机过程,其合并时间本身具有较大方差(参见第3章)。这导致即使$N_{e}$恒定,错配分布形态仍存在较大变异。因此,基于错配分布的检验仅能检测$N_{e}$发生极大且持续收缩或扩张的情况。
| |
|
| |
| #### Tajima's D检验
| |
| Tajima's $D$是对标准溯祖模型(恒定种群大小下的中性等位基因)的检验方法,常用于分析单一物种的DNA多态性数据(Tajima 1989a,b)。该检验通过DNA序列样本中的核苷酸多样性(nucleotide diversity)和分离位点(segregating sites)数量,对尺度突变率$\uptheta=4N_{e}\upmu$进行两次估计。本节将基于核苷酸多样性的θ估计记作$\hat{\boldsymbol{\theta}}_{\pi}$,基于分离位点数的θ估计记作$\hat{\boldsymbol{\theta}}_{S}$。Tajima's $D$检验的原理是:在标准溯祖模型(所有突变中性且种群大小恒定)下,$\hat{\boldsymbol{\theta}}_{\pi}$与$\hat{\boldsymbol{\theta}}_{S}$应大致相等。该检验的零假设为:DNA序列样本来自有效种群大小恒定且所有突变中性的种群。若DNA序列受自然选择作用或有效种群大小随时间变化,则将导致零假设被拒绝。
| |
|
| |
| 
| |
|
| |
| ```markdown
| |
| 图 8.25 基因谱系形状的差异是Tajima's $D$检验的基础。在标准的溯祖模型(coalescent model)中,谱系分支的合并概率随时间推移在每个谱系中是恒定的。因此,当所有等位基因呈选择中性且有效种群大小恒定时,标准溯祖模型给出了预期的分支长度(中图)。随时间变化的有效种群大小(种群增长、种群瓶颈)也会改变合并概率随时间的变化。自然选择同样会根据每个谱系携带等位基因的适合度改变合并概率。有效种群大小的变化和自然选择会改变预期的合并时间,从而改变基因谱系树中的预期分支长度。如果当前的合并概率比过去更大(右图),则大多数合并事件会发生在近期,且内部分支相比外部分支更长。如果当前的合并概率比过去更小(左图),则大多数合并事件发生在过去,且外部分支相比内部分支更长。由于突变发生的概率随时间恒定,较长分支的谱系预期会经历更多突变。
| |
|
| |
| Tajima's $D$利用了以下事实:在计算所有独特序列对的核苷酸多样性(π)时,基因谱系中发生时间更早的突变会被重复计数更多次。相反,突变在基因谱系上的位置不会影响分离位点(S)的数量,因为携带特定核苷酸的序列数量无论多少都仅代表一个分离位点(图 8.25)。当有效种群大小恒定且仅有遗传漂变作用时,溯祖过程会导致基因谱系中内部和外部分支的总长度大致相等(存在显著随机变异)。相反,改变合并概率的过程也会改变内部和外部分支长度的比例,从而改变$\pi$和S的值,最终影响Tajima's $D$(图 8.26)。通常认为Tajima's $D<0$表示存在定向选择或选择性清除(参见Braverman et al. 1995),而Tajima's $D>0$则表示某个位点上的两个等位基因经历了平衡选择。然而,有效种群大小随时间持续增长或针对三个及以上等位基因的平衡选择都可能降低近期合并的概率,导致外部分支更长。有效种群大小随时间急剧缩减或种群瓶颈则预期会增加近期合并的概率,从而缩短外部分支。此外,种群分化也会影响Tajima's D:若从多个分化的地方种群(deme)中采样谱系,基因谱系的外部分支会较长;若从两个分化地方种群采样谱系,则内部分支会较长。
| |
|
| |
| 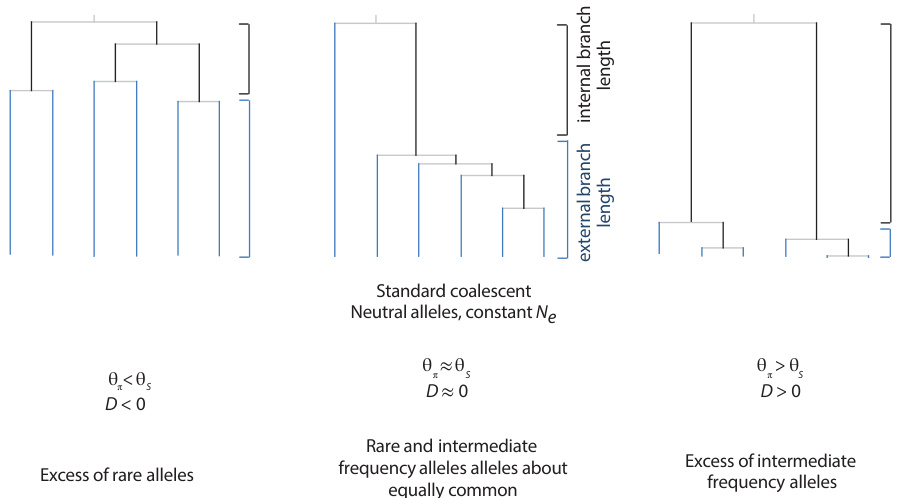</pre>
| |
| 图 8.26 错配分布的基础。A图展示了一个包含多个突变事件的中性系谱。每个突变事件用圆圈表示,并标注了在无限位点突变模型下发生突变的随机核苷酸位点编号。根据种群中仅存在两个谱系时的祖先关系,现存的六个谱系可被分为两组(称为A和B)。B图显示了每个谱系的DNA序列,基于最近共同祖先(MRCA)分配的30个碱基对序列,其中突变以小写字母表示。C图展示了DNA序列对之间不同的核苷酸位点数量(即错配数)。D图中的错配分布是对15对DNA序列比较的错配数直方图。在有效种群大小<math display="inline">N_{e}</math>长期恒定的种群中,中性系谱倾向于呈现双峰型错配分布。少量错配的观测值聚类来源于近期相关谱系之间的序列比较(组A或组B内部比较)。相反,当<math display="inline">k=2</math>时不共享同一祖先的远缘谱系(组A与组B之间比较)的序列往往具有更多错配。
| |
|
| |
| 理解Tajima’s <math display="inline">D</math>的另一种方式,是考虑不同自然选择类型或种群统计学下的等位基因频率分布。发生在系谱内部分支的突变具有中等频率,因为它们会被后续产生的谱系继承。相反,发生在外部分支的突变频率较低,因为它们仅存在于单一谱系。在标准溯祖模型下,总内部分支长度与总外部分支长度预期大致相等,因此中等频率与稀有等位基因的频率分布也应大致均衡。强烈的种群增长或多等位平衡选择会导致稀有突变过量,因为这些过程增加了外部分支长度。相反,强烈纯化选择、种群规模急剧缩小或种群瓶颈会导致中等频率突变过量,因为这些过程增加了内部分支长度。
| |
|
| |
| Tajima’s <math display="inline">D</math>统计量通过<math display="inline">\hat{\boldsymbol{\theta}}_{\pi}</math>与<math display="inline">\hat{\boldsymbol{\theta}}_{S}</math>的差值除以标准差计算:
| |
|
| |
| <math display="block">
| |
| D={\frac{{\hat{\theta}}_{\pi}-{\hat{\theta}}_{S}}{\sqrt{\operatorname{var}\left({\hat{\theta}}_{\pi}-{\hat{\theta}}_{S}\right)}}}={\frac{{\hat{\theta}}_{\pi}-{\frac{p_{S}}{a_{1}}}}{\sqrt{e_{1}p_{S}+e_{2}p_{S}(p_{S}-1)}}}
| |
| </math>
| |
|
| |
| 其中<math display="inline">p_{S}</math>表示每个核苷酸位点的分离位点数。注意标准差是方差的平方根,因此除以标准差可将<math display="inline">D</math>转换为以标准偏差为单位的度量,其均值0对应标准溯祖系谱。仅当观测结果偏离均值约两个标准偏差时,我们才拒绝<math display="inline">D=0</math>的原假设,从而拒绝”中性系谱且有效种群大小恒定”的零模型(参见Tajima 1989a表2中的置信限)。
| |
|
| |
| 用于计算方差的量为:
| |
|
| |
| <math display="block">
| |
| e_{1}=\frac{n+1}{3a_{1}(n-1)}-\frac{1}{a_{1}^{2}}
| |
| </math>
| |
|
| |
| 以及
| |
|
| |
| <math display="block">
| |
| e_{2}={\frac{c}{a_{1}^{2}+a_{2}}}
| |
| </math>
| |
|
| |
| 其中
| |
|
| |
| <math display="block">
| |
| \begin{array}{c}{{a_{1}=\displaystyle\sum_{k=1}^{n-1}\frac{1}{k}}}\ {{{}}}\ {{a_{2}=\displaystyle\sum_{k=1}^{n-1}\frac{1}{k^{2}}}}\end{array}
| |
| </math>
| |
|
| |
| 且
| |
|
| |
| 虽然<math display="inline">D</math>的方差是一个复杂的表达式,但仍可直观理解。该公式同时包含抽样方差和进化方差。抽样方差源于从DNA序列中取样并用其估计<math display="inline">\pi</math>和<math display="inline">S</math>。与从更大基础群体中获取任何有限样本数据的情况类似,重复抽样过程会因样本不能完美代表整个群体而导致参数估计的微小差异。抽样方差随样本量增加而减小,因为估计值基于基础群体中越来越大的比例。相反,进化方差由遗传漂变和突变等随机进化过程的不同结果引起。进化方差只能通过采样同一随机过程的多个独立实现来估计,例如:从同一祖先群体隔离后经历独立遗传漂变的多个群体中采集DNA序列样本。溯祖和
| |
|
| |
| <math display="block">
| |
| c=\frac{2(n^{2}+n+3)}{9n(n-1)}-\frac{n+2}{a_{1}n}+\frac{a_{2}}{a_{1}^{2}}
| |
| </math>
| |
|
| |
| 其中<math display="inline">n</math>为采样的序列数量,并假设不存在重组。
| |
|
| |
| <span id="问题框8.2-从dna序列数据计算tajimas-d"></span>
| |
| = 问题框8.2 从DNA序列数据计算Tajima’s D =
| |
|
| |
| 为研究_D. simulans_的群体历史,Baudry等(2006)从非洲、欧洲和安的列斯群岛的多个种群中采样果蝇。他们测定了位于X染色体上的四个基因。利用部分DNA序列数据,通过Tajima’s D检验_D. simulans_是否符合标准中性溯祖模型的假设。
| |
|
| |
| 欧洲和马约特(法国海外行政区,由印度洋中马达加斯加北部与莫桑比克北部之间的多个岛屿组成)采样果蝇的runt基因座DNA序列呈现以下模式:
| |
|
| |
| {|
| |
| ! Population
| |
| ! nsequences
| |
| ! Nucleotide sites
| |
| ! S
| |
| ! π
| |
| |-
| |
| | Europe
| |
| | 15
| |
| | 556
| |
| | 17
| |
| | 0.012436
| |
| |-
| |
| | Mayotte
| |
| | 15
| |
| | 538
| |
| | 34
| |
| | 0.013525
| |
| |}
| |
|
| |
| 使用分离位点数<math display="inline">(S)</math>计算每核苷酸位点的分离位点数<math display="inline">(p_{S})</math>,然后根据式8.32估计每位点的<math display="inline">\hat{\theta}_{S}</math>。接着按式8.60计算Tajima’s <math display="inline">D</math>。
| |
|
| |
| 你对这两个_D. simulans_种群的演化历史有何结论?注意你的Tajima’s <math display="inline">D</math>估计值会与Baudry等(2006)不同,因为他们仅使用同义位点多态性数据,而你使用了所有位点的多态性。为何Baudry等(2006)仅使用同义位点多态性?DNA序列数据文件可在教材网站获取。
| |
|
| |
| 突变过程均具有显著的进化方差。例如,在标准溯祖模型下,<math display="inline">k</math>个谱系的溯祖时间在平均值附近存在广泛波动,且两个谱系的溯祖时间方差最大(见第3.6节)。
| |
|
| |
| Tajima’s <math display="inline">D</math> 的数值受到种群大小随时间变化、种群结构和自然选择作用的影响。因此,Tajima’s <math display="inline">D</math> 并不能像有时假设的那样单独作为检验自然选择作用的简单测试(参见 Fu 1997;Li 2011)。零模型基于随时间恒定的突变速率(分子钟)、突变的无限位点模型、非重叠世代的Wright-Fisher模型,以及处于漂变-突变平衡状态的随机交配种群(关于前两点参见 Tajima 1996)。尽管较大的 <math display="inline">D</math> 值可用于拒绝标准溯祖模型对特定DNA多态性数据的适用性,但要区分随时间变化的有效种群大小、种群结构和自然选择的影响仍具挑战性。随时间推移影响有效种群大小的群体历史变化,或由有效迁移率导致的种群分化,预计会影响所有位点。相反,自然选择预期是基于位点多态性对适应度的影响而逐个位点发生的现象。因此,比较多个位点的 <math display="inline">D</math> 估计值是推断塑造遗传多态性模式过程的一种方法。例如,人类中许多基因的DNA多态性模式常显示Tajima’s <math display="inline">D</math> 的负值。这些结果目前普遍被认为是由较低的种群结构水平以及近期人类种群快速扩张的历史所导致,而非平衡选择对多个人类位点的独立作用(Ptak and Przeworski 2002;Tishkoff and Verrelli 2003)。
| |
|
| |
| Tajima’s <math display="inline">D</math> 检验用于比较两种序列多态性度量,其中 <math display="inline">\uptheta_{\pi}</math> 对中等频率等位基因最敏感,而 <math display="inline">\uptheta_{\mathrm{S}}</math> 对低频等位基因最敏感(参见 Zeng et al. 2006)。其他几种检验方法也被提出,它们比较相关的序列多态性度量但捕捉等位基因频率分布中的不同模式。这些检验利用样本中出现次数为 <math display="inline">i</math> 的序列与祖先序列存在差异的位点数 <math display="inline">\xi_{\mathrm{i}}</math>(本章前文已描述)。这些检验基于自然选择对等位基因频率分布的若干预测。其中一个预测是:选择扫荡将导致一个单体型达到高频——即经历有利突变的位点及其连锁位点多态性。任何发生在该高频单体型上的近期突变都将存在并产生低频等位基因池。第二个预测有助于判断是正选择还是背景选择可能作用于单体型频率的改变。作为选择扫荡基础的新有利突变是衍生单体型状态。相反,背景选择通过从种群中移除有害突变来维持祖先单体型。因此,使用外群序列可显示哪些单体型是祖先型,哪些是衍生型,从而帮助区分正选择与背景选择。
| |
|
| |
| Fay和Wu(2000)提出使用
| |
|
| |
| $$
| |
|
| |
| <math display="block">
| |
| H=\hat{\boldsymbol{\theta}}_{\pi}-\hat{\boldsymbol{\theta}}_{H}
| |
| </math>
| |
|
| |
| 用于比较对中等频率等位基因最敏感 <math display="inline">(\hat{\boldsymbol{\theta}}_{\pi})</math> 和对高频等位基因最敏感 <math display="inline">(\hat{\theta}_{H})</math> 的序列多态性度量。<math display="inline">H</math> 的小值表明相较于中性模型存在高频衍生等位基因的过量,这与正选择一致。Fay和Wu的<math display="inline">H</math>对种群规模的剧烈增减不如Tajima的<math display="inline">D</math>敏感,因为此类群体数量变化预期对低频等位基因影响最大,而对那些在谱系中突变起源更深远的高频等位基因影响较小。
| |
|
| |
| Zeng等(2006)提出通过除以<math display="inline">\hat{\theta}_{\pi}-\hat{\theta}_{H}</math>的标准差来标准化Fay和Wu的<math display="inline">H</math>。由于Tajima的<math display="inline">D</math>和Fay与Wu的<math display="inline">H</math>都以中等频率等位基因作为比较基准,他们还建议使用
| |
|
| |
| <math display="block">
| |
| E={\frac{{\hat{\theta}}_{L}-{\hat{\theta}}_{S}}{\sqrt{\operatorname{var}\left({\hat{\theta}}_{L}-{\hat{\theta}}_{S}\right)}}}
| |
| </math>
| |
|
| |
| 作为比较低频与高频等位基因度量的额外统计量。<math display="inline">E</math>的负值为研究位点经历选择性清除后预期出现的低频等位基因恢复提供证据。Zeng等(2006)还描述了将<math display="inline">D</math>和<math display="inline">H</math>合并为联合检验的方法。他们的模拟展示了如何利用这一系列相关检验来检测对中性模型和恒定种群规模假设的偏离。例如,Tajima的<math display="inline">D</math>、<math display="inline">H</math>和联合<math display="inline">DH</math>的检验效力随着有利突变频率增加而快速提升,但<math display="inline">E</math>在有利等位基因固定后成为检测正选择更有效的检验。此外,<math display="inline">D</math>和<math display="inline">E</math>对种群增长敏感,而<math display="inline">H</math>对种群规模缩减最敏感。
| |
|
| |
| 作为正选择的检验方法,Li(2011)提出单独使用观测到的衍生突变最大频率<math display="inline">(\xi_{\mathrm{max}})</math>来判断中性模型下观测到特定<math display="inline">\xi_{\mathrm{max}}</math>水平的概率。<math display="inline">\xi_{\mathrm{max}}</math>检验被设计为对种群规模变化、背景选择或群体分化的混杂效应不敏感。
| |
|
| |
| 这些都强调了位点频谱的多种度量是样本采集方式、被采样序列进化历史的函数,且观测到的多态性受到所有塑造谱系的群体遗传过程的影响。
| |
|
| |
| <span id="谱系分支模型中的重组"></span>
| |
| ==== 8.7 谱系分支模型中的重组 ====
| |
|
| |
| 谱系与重组。<br />
| |
| 祖先重组图。<br />
| |
| 重组的后果。
| |
|
| |
| 重组通过产生现有单倍型的新组合并改变现有单倍型的频率,在产生遗传多态性中发挥重要作用。通过从基本溯祖模型出发,并添加另一种可能发生的事件类型(从现生群体向过去追溯至所有谱系找到其MRCA的时间过程中),可以描述含重组的谱系历史(Hudson 1983)。我们将再次利用指数分布的特性来近似事件发生的等待时间(见第3.6节)。
| |
|
| |
| 让我们从具有相等雌雄群体大小(<math display="inline">N_{m}=N_{f}</math>)的二倍体有性生物群体中的重组开始分析。图8.27A展示了一代内的遗传过程:时间t个体的两条染色体分别来自时间t-1的一个父本和一个母本。在亲本中,染色体可能发生重组,使得传递给子代的染色体是两条亲本染色体的新组合。例如,时间t的父系谱系3从其父系祖先(谱系2)继承了一条重组染色体。由于群体有限,时间t-1的亲本谱系有可能成为时间t两个子代染色体的共同祖先,例如母系谱系1和2都从父系祖先(时间t-1的父系谱系4)继承了相同的染色体。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/8032b260d97d9c7675f71d8961392dc381231bf92ae57e98ec58342974469f76.jpg]]<br />
| |
| 图8.27 含重组可能的溯祖事件背景下二倍体(A)和单倍体(B)的繁殖过程。在二倍体群体中,现生个体内的两条染色体分别来自雌性群体(<math display="inline">N_{f}</math>)和雄性群体(<math display="inline">N_{\mathrm{m}}</math>)的一个祖先。此外,祖先染色体可能发生重组,使得现生染色体不同区段源自过去两条染色体。在单倍体群体中,溯祖概率为<math display="inline">\textstyle{\frac{1}{2N}}</math>(实线),而两条谱系在前一代没有共同祖先的概率为<math display="inline">\textstyle1-{\frac{1}{2N}}</math>(实线)。重组事件(虚线)导致谱系在时间回溯时发生分叉,因为现生染色体不同区段源自过去两个祖先。与基本溯祖模型类似,使用具有2N条谱系的单倍体群体来近似模拟具有<math display="inline">2N=N_{\mathrm{f}}+N_{\mathrm{m}}</math>个体的二倍体群体。
| |
|
| |
| 含重组的溯祖过程可通过使用大小为2N的单倍体群体(图8.27B)进行近似,这与基本溯祖模型的方法一致。在时间回溯过程中,谱系随机选择祖先染色体,当两条谱系共享同一祖先时发生溯祖事件。同时,重组可能发生,导致染色体在重组点两侧的区段具有不同祖先。图8.27B展示了谱系2的重组情况:其染色体的一部分源自谱系1,另一部分源自谱系2。
| |
|
| |
| 对于溯祖(coalescence)和重组(recombination),可以构建一个祖先重组图(ancestral recombination graph)(Griffiths 1991; Griffiths 和 Marjoram 1997)或 ARG(图 8.28)。重组事件会导致在时间回溯过程中增加谱系来表示重组事件。(由于它们共享一种在时间回溯过程中增加谱系的机制,祖先重组图与第7章描述的祖先选择图以相似的方式运作。)任何由重组产生的谱系随后可以与随机抽样的谱系在更早的时间点发生溯祖。由于重组的作用,不同位点(或染色体片段)可能具有不同的谱系和不同的最近共同祖先(MRCA)。尽管重组事件在时间回溯过程中增加了分支,但溯祖过程更快,最终会导致所有谱系溯祖至单一祖先(溯祖速率与<math display="inline">k^{2}</math>成正比,而重组速率与<math display="inline">k</math>成正比)。所有可能发生重组的位点的单一祖先被称为最远最近共同祖先(grandmost recent common ancestor,GMRCA)。
| |
|
| |
| [[File:https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/654a188c11683636b57b1e216257cc3ed896ae2ca939ce8d20efe494af181873.jpg]]<br />
| |
| '''图 8.28''' 包含三个位点突变和六个谱系的祖先重组图(A)。事件类型和事件间相对时间显示在右侧标尺上。面板 B 展示了在解析面板 A 谱系上的重组事件后,三个位点各自的谱系。由于重组作用,三个位点的谱系相关但不完全相同。
| |
|
| |
| 单倍体模型假设溯祖和重组事件相互独立且发生频率足够低,因此它们不会同时发生(或当<math display="inline">N</math>很大且重组速率较小时),从而在时间回溯过程中发生的事件只能是溯祖或重组。当事件独立时,所有可能事件的概率相加即可得到事件发生的总概率。因此,若我们对每一代的重组概率采用指数近似,则可直接将其与溯祖概率的指数近似相加。
| |
|
| |
| 每个谱系在每一代经历重组的速率为<math display="inline">c</math>。因此,一个谱系未经历重组的概率为每代<math display="inline">1-c</math>。单个谱系在经历<math display="inline">t</math>代后首次发生重组的概率即为前<math display="inline">t-1</math>代未发生重组而第<math display="inline">t</math>代发生重组的概率:
| |
|
| |
| <math display="block">
| |
| P(T_{recombination}=t)=\left(1-c\right)^{t-1}c
| |
| </math>
| |
|
| |
| 该公式与之前章节中描述的溯祖、迁移或突变事件在<math display="inline">t</math>代后发生的概率形式相同。与溯祖概率类似,随时间变化的重组概率是一个几何级数,可用指数分布近似(见数学框 3.2)。
| |
|
| |
| 要获得重组过程的指数分布,我们需要确定种群中预期发生重组的速率。如果定义 <math display="inline">\mathrm{\Delta}\mathrm{\phi}=4N c</math>,则 <math display="inline">\uprho/2</math> 等价于 <math display="inline">2N c</math> 或每代在 2N 个谱系种群中预期的重组事件数,也称为种群重组率。当时间以连续尺度测量时,一个时间单位相当于 2Nc 个离散世代,或在一单位连续时间内种群中预期发生 <math display="inline">2N c</math> 次重组事件。
| |
|
| |
| 种群重组率的定义导出了谱系在恰好第 t 代经历重组的概率的指数近似:
| |
|
| |
| <math display="block">
| |
| P(T_{recombination}=t)=e^{-t_{2}^{\rho}}
| |
| </math>
| |
|
| |
| 当存在多于一个谱系时,每个谱系有独立的重组机会,因此每个谱系的 <math display="inline">e^{-t_{2}^{\rho}}</math> 重组概率需对所有 <math display="inline">k</math> 个谱系求和以获得总重组概率:
| |
|
| |
| <math display="block">
| |
| P(T_{recombination}=t)=e^{-t_{2}^{\rho}k}
| |
| </math>
| |
|
| |
| 对于 <math display="inline">k</math> 个谱系。<math display="inline">k</math> 个谱系中某一个在或早于某时间发生重组事件的概率可通过累积指数分布近似:
| |
|
| |
| <math display="block">
| |
| P(T_{recombination}\leq t)=1-e^{-t_{2}^{\rho}k}
| |
| </math>
| |
|
| |
| 其方式与近似共祖事件时间的处理完全相同。
| |
|
| |
| 当两个独立过程同时作用时,系谱模型变为沿时间回溯谱系并等待事件发生的形式。此时可能的事件为重组或共祖,因此任何事件的总概率是各类型独立事件概率之和。当回溯时间时(增加 <math display="inline">t_{\prime}</math>),发生任一事件(共祖或重组)的总概率为:
| |
|
| |
| <math display="block">
| |
| \begin{array}{r}{P(T_{event}\leq t)=1-e^{-t\left[k_{2}^{\rho}+\frac{k(k-1)}{2}\right]}}\end{array}
| |
| </math>
| |
|
| |
| 其中指数项是重组和共祖强度的总和。
| |
|
| |
| 当由式 8.72 的指数分布给出事件发生时间后,需判定该事件是共祖还是重组。事件为重组或共祖的总概率为 <math display="inline">k{\frac{\rho}{2}}+{\frac{k(k-1)}{2}}</math>。因此,事件为重组的概率为:
| |
|
| |
| <span id="interact-box-8.5-build-an-ancestral-recombination-graph"></span>
| |
| = Interact Box 8.5 Build an Ancestral Recombination Graph =
| |
|
| |
| 可通过累积指数分布确定事件等待时间来构建包含重组可能性的共祖系谱。一旦获得等待时间,利用两类事件的概率判定该事件是共祖还是重组。若为共祖,则随机选择一对谱系合并,谱系数目(k)减 1。若为重组,则随机选择一个谱系分岔生成两个新谱系。
| |
|
| |
| 步骤 1:在 <math display="inline">k</math> 个谱系时,使用指数分布抽取到下一事件的时间。<br />
| |
| 步骤 2:判定该事件是共祖还是重组。
| |
|
| |
| 步骤 3A:如果是溯祖事件(coalescent event),在等待时间结束后随机选择两个谱系进行溯祖。用实线标记这些谱系。将<math display="inline">\mathsf{k}</math>减少1。<br />
| |
| 步骤 3B:如果是重组事件(recombination event),在等待时间结束后随机选择一个谱系生成新的重组分支。用虚线标记重组谱系。将<math display="inline">\mathsf{k}</math>增加1。<br />
| |
| 步骤 4:如果<math display="inline">\mathsf{k}\geq2</math>,返回步骤1。否则,已追溯至GMRCA(全基因组最远共同祖先)。<br />
| |
| 步骤 5:为GMRCA分配一条祖先染色体(DNA序列或多位点单倍型)。从GMRCA开始,沿时间正向追踪所有分支,每个谱系携带其祖先单倍型状态。由重组产生的虚线谱系携带其祖先染色体的一段,该段通过沿染色体随机分配重组点并将祖先染色体分为两部分确定。其中一部分染色体沿虚线传递,并与连接谱系携带的互补单倍型片段配对,形成重组染色体。注意:需引入突变才能观察到重组对谱系拓扑的影响(否则所有谱系均携带祖先单倍型),因此可假设若干突变事件。
| |
|
| |
| 教材官网提供R脚本和Microsoft Excel表格用于计算含重组的溯祖谱系所需参数。
| |
|
| |
| <math display="block">
| |
| {\frac{k{\frac{\rho}{2}}}{k{\frac{\rho}{2}}+{\frac{k(k-1)}{2}}}}={\frac{\rho}{\rho+k-1}}
| |
| </math>
| |
|
| |
| 而事件为溯祖的概率为重组点。因此,重组事件会导致祖先数量随时间回溯而增加,谱系数量变为<math display="inline">\mathsf{k}+1</math>。
| |
|
| |
| ==== 重组的影响 ====
| |
|
| |
| <math display="block">
| |
| {\frac{\frac{k(k-1)}{2}}{k{\frac{\rho}{2}}+{\frac{k(k-1)}{2}}}}={\frac{k-1}{\rho+k-1}}
| |
| </math>
| |
|
| |
| 将左侧表达式乘以<math display="inline">\frac{{{2}\mathord{\left/{\vphantom{{2}}}\right.\kern-\nulldelimiterspace}k}}{{{2}\mathord{\left/{\vphantom{{2}}}\right.\kern-\nulldelimiterspace}k}}</math>后可得。当事件为溯祖时,随机选择两个谱系进行合并,<math display="inline">\mathsf{k}</math>减1。当事件为重组时,随机选择一个单倍型并沿其染色体随机选取一个点,随后为被重组点分隔的两个染色体片段分别随机选择两个祖先【“segments”译为“片段”】。
| |
|
| |
| 祖先重组图(ancestral recombination graph)展示了在没有重组的情况下,单倍型上多个位点如何相互关联并共享同一谱系。相反,被重组断点分隔的单倍型上不同位点则相互独立,可能具有不同的谱系。染色体上各位点谱系间的关联程度与重组率成反比,这为理解连锁不平衡(linkage disequilibrium)提供了另一种视角(McVean 2002)。重组的一个结果涉及分离位点的数量:虽然重组不改变分离位点的平均数(S),但随着群体重组率(4Nc)的增加,S的方差会减小(Hudson 1983)。这是因为随着更多位点获得独立谱系,由溯祖时间贡献的S方差减少,使得突变过程贡献的总方差比例增大(见式8.29)。
| |
|
| |
| 祖先重组图作为概念工具可用于预测重组对中性DNA序列多态性模式的可能影响。然而,ARG作为从经验DNA序列数据估计群体遗传参数(如群体重组率)的框架显得笨拙(Rasmussen et al. 2014; Hubisz and Siepel 2020)。其中一个挑战在于,在ARG中,样本历史中的某些染色体片段可能不属于当前谱系样本的染色体。这些被”困住”的染色体片段使得从观测数据估计ARG的历史变得困难。在另一种方法中,带有重组的溯祖过程被重构为沿染色体长度顺序运行的过程(Wiuf and Hein 1999)。这种被称为顺序溯祖(sequential coalescent)的方法将染色体划分为多个核苷酸片段,每个片段具有由漂变和突变生成的谱系,这些位点谱系通过历史重组事件模式相互关联。顺序溯祖的难点在于它不满足马尔可夫性质,因为染色体上相邻位点的谱系依赖于所有先前位点的谱系。恢复无记忆特征的顺序溯祖模型近似方法被称为顺序马尔可夫溯祖(sequentially Markovian coalescent,SMC)(如McVean and Cardin 2005; Wilton et al. 2015)。不同版本的SMC模型为简化计算仅考虑连锁片段中的部分可能溯祖事件(例如仅考虑单倍型对的溯祖事件),然后使用隐马尔可夫模型方法从观测DNA序列数据估计与溯祖过程相关的群体参数,以推断历史群体动态(Spence et al. 2018)。最终得到基因组各片段的溯祖时间分布,其中峰值出现在基因组较大比例具有共同祖先的时期(如群体瓶颈期)。
| |
|
| |
| <span id="第8章-复习"></span>
| |
| = 第8章 复习 =
| |
|
| |
| 中性理论是分子演化中广泛使用的零假设,其预测DNA序列变化的模式和速率基于所有突变均无适应度优势或劣势的假设。尽管遗传漂变导致固定或丢失,中性等位基因会经历随机游走达到这些终点,从而产生瞬态遗传变异。<br />
| |
| 中性理论预测多态性(即种群内的遗传变异)是有效种群大小和突变率的函数。更大的有效种群规模或更高的突变率会导致更高的平衡多态性水平。中性理论预测分歧速率(即两个物种间固定核苷酸差异的积累)仅由突变率决定。<br />
| |
| 近中性理论假设许多突变实际上是中性的,因为它们的选择系数小于遗传漂变的压力。当<math display="inline">4N_{e}s=1</math>时,遗传漂变和自然选择对新生突变命运的支配概率相等。<br />
| |
| 分子演化的中性理论提出引发了”中性论者”与支持选择驱动解释分歧速率和多态性水平的学者之间的争议。中性-选择之争推动了对遗传漂变和自然选择理论预期的诸多创新。<br />
| |
| 核苷酸位点受到定向自然选择的作用,导致对有害等位基因的净化(或负向)选择和对有利等位基因的正向选择。自然选择还通过重组率的调节间接改变关联中性位点的多态性水平。<br />
| |
| 平衡选择可增加受选择位点的多态性,以及与这些位点连锁的中性位点的多态性——这些中性位点因漂变预期更长的分离时间,从而积累更多中性突变。<br />
| |
| 遗传搭车会降低邻近位点的多态性,因为正向选择会使有益突变及其连锁的中性突变同时固定。这导致选择性清除现象,即连锁位点的多态性被消除。
| |
|
| |
| = 选择性扫荡与多态性 =
| |
|
| |
| '''硬选择性扫荡'''(hard selective sweeps)是强选择作用于单个有利突变的结果,会导致连锁位点多态性的最大程度丢失。'''软选择性扫荡'''(soft selective sweeps)是选择作用于现存多态性或作用于多个位点上的有利等位基因的结果,其多态性减少程度较低。
| |
|
| |
| '''负选择'''(negative selection)会驱动有害突变与连锁位点上的中性突变共同丢失,这一过程称为'''背景选择'''(background selection),从而减少多态性。中性核苷酸位点的分化速率不受连锁核苷酸位点上自然选择的影响。
| |
|
| |
| 两条DNA序列之间的表观分化可能因多重击中突变(multiple-hit mutations)或'''同塑性'''(homoplasy)而被低估。核苷酸替换模型用于校正观察到的分化值以修正多重击中的影响,从而更准确估计实际分化程度。
| |
|
| |
| '''核苷酸多样性'''(nucleotide diversity,<math display="inline">\pi</math>)与'''分离位点数'''(number of segregating sites,<math display="inline">S</math>)是两种衡量DNA序列多态性的指标,可用于估计<math display="inline">\uptheta=4N_{e}\upmu</math>。'''分子钟假说'''(molecular clock hypothesis)基于中性理论的预测——分化以恒定速率随时间发生,从而估计两条序列自共同祖先分异以来经历的时间。
| |
|
| |
| 分化速率随时间推移的异质性(heterogeneity)普遍存在,导致难以将分化程度等同于分异时间。在泊松过程(Poisson process)模型下,替换速率的方差应等于平均替换速率,此时离散指数(index of dispersion)为1。实际中离散指数常不等于1,表明替换速率并非完全由中性过程决定,或泊松模型无法准确描述中性替换过程。
| |
|
| |
| 速率异质性可能与中性进化一致,例如当突变速率每代恒定但世代时间跨度不同时。此外,速率异质性也可能由自然选择引起,即选择通过改变突变的适合度来影响其替换概率。
| |
|
| |
| '''HKA检验'''与'''MK检验'''验证中性理论的预测:多态性与分化应成比例,因为二者均为突变速率的函数。
| |
|
| |
| '''错配分布'''(mismatch distributions)是基因谱系分支模式的产物,在标准中性模型(种群规模恒定且随机交配)下预期呈双峰型。'''Tajima’s <math display="inline">D</math>'''通过比较基于平均成对差异值估计的θ与基于分离位点数估计的θ来检验中性假设,二者在中性、种群规模恒定且随机交配的零模型下应相等。
| |
|
| |
| DNA序列多态性可通过多种指标表征,这些指标对低频、中频或高频等位基因赋予不同权重,而种群增长或自然选择等过程对这些等位基因的影响存在差异。'''祖先重组图'''(ancestral recombination graph)将溯祖(coalescent)与重组结合,显示核苷酸位点的谱系如何因历史重组事件的相关性或独立性而呈现不同模式。
| |
|
| |
| <span id="延伸阅读-3"></span>
| |
| = 延伸阅读 =
| |
|
| |
| Motoo Kimura对中性理论进行了通俗阐释:
| |
|
| |
| Kimura, M. (1989). The neutral theory of molecular evolution and the world view of neutralists. ''Genome''
| |
|
| |
| <span id="章末练习题-1"></span>
| |
| = 章末练习题 =
| |
|
| |
| # 假设从某个种群和基因座中抽取了<math display="inline">k=6</math>个谱系样本,其中<math display="inline">\uptheta=5</math>。每个基因座的预期分离位点数量是多少?预期分离位点数的方差是多少?假设了何种突变模型使得在确定预期分离位点数时无需知道被取样的核苷酸数量?
| |
| # 使用图8.15中的示例数据,计算<math display="inline">\hat{\boldsymbol{\theta}}_{S},\hat{\boldsymbol{\theta}}_{\pi},\hat{\boldsymbol{\theta}}_{L}</math>和<math display="inline">\hat{{\boldsymbol{\theta}}}_{H}</math>。解释这四种不同估计量如何对不同类型的序列差异进行加权。通过在该假设数据集中增加更多分离位点或更多序列,说明低频、中频和高频等位基因如何影响这四种测度。
| |
|
| |
|
| |
| -----
| |
|
| |
| '''文献综述部分翻译'''(注:仅按格式要求调整,保留原始文献信息)
| |
|
| |
| 关于近中性理论的综述,参见:<br />
| |
| Ohta, T. (1992). The nearly neutral theory of molecular evolution. ''Annual Reviews of Ecology and Systematics'' 23: 263–286.
| |
|
| |
| 关于中性理论作为分子多态性与分化解释核心原理的简明总结,参见:<br />
| |
| Jensen, J.D., Payseur, B.A., Stephan, W. et al. (2019). The importance of the neutral theory in 1968 and 50 years on: a response to Kern and Hahn 2018. ''Evolution'' 73: 111–114.
| |
|
| |
| 关于连锁与突变背景下自然选择模型的综述及实证研究综合,参见:<br />
| |
| Cutter, A.D. and Payseur, B.A. (2013). Genomic signatures of selection at linked sites: unifying the disparity among species. ''Nature Reviews Genetics'' 14: 262–274.
| |
|
| |
| 关于选择性清除多种模型的综述与综合,参见:<br />
| |
| Stephan, W. (2019). Selective sweeps. ''Genetics'' 211: 5–13.
| |
|
| |
| 关于分子钟校准与估计方法及估算软件的概述,参见:<br />
| |
| Ho, S.Y.W. and Duchêne, S. (2014). Molecular-clock methods for estimating evolutionary rates and timescales. ''Molecular Ecology'' 23: 5947–5965.
| |
|
| |
| 关于利用定向选择或平衡选择解释观测多态性的实证研究综述,参见:<br />
| |
| Hedrick, P.W. (2006). Genetic polymorphism in heterogeneous environments: the age of genomics. ''Annual Review of Ecology Evolution and Systematics'' 37: 67–93.
| |
|
| |
| 关于使用DNA序列多态性与分化数据进行自然选择假设检验的广泛方法综述,参见:<br />
| |
| Vitti, J.J., Grossman, S.R., and Sabeti, P.C. (2013). Detecting natural selection in genomic data. ''Annual Review of Genetics'' 47: 97–120.
| |
|
| |
| 关于序贯马尔可夫溯祖理论及其种群基因组推断方法的简明导论,参见:<br />
| |
| Mather, N., Traves, S.M., and Ho, S.Y.W. (2020). A practical introduction to sequentially Markovian coalescent methods for estimating demographic history from genomic data. ''Ecology and Evolution'' 10: 579–589.
| |
|
| |
| 3 试想,在众多经历局部适应的亚群体中,不同等位基因频率的分化由少数受选择作用的位点驱动,而大多数位点则在漂变和基因流下演化。基于你对选择扫荡和背景选择的理解,预测全基因组范围内大量SNP的<math display="inline">F_{ST}</math>与重组率之间会呈现何种关系?(有关人类群体中的预测与检验讨论,参见Keinan和Reich 2010的研究。)
| |
|
| |
| 4 在文献中检索近期利用本章所述群体遗传学预测的研究论文。主题可涉及任意生物、应用或过程,但论文必须包含对中性及近中性理论、纯化或背景选择、选择扫荡、Tajima’s <math display="inline">D</math>、HKA检验、遗传搭车、分子钟等主题的假设检验。总结论文的核心假设、目标或理论基础,并阐明该研究如何运用本章的群体遗传学预测,最后归纳基于该预测的研究结果与结论。
| |
|
| |
| = 习题框8.1答案 =
| |
|
| |
| 小麦与玉米的分化时间为6000万年前,其分化速率为:
| |
|
| |
| 使用这些绝对分化速率,单子叶植物与双子叶植物的分化时间估计为:
| |
|
| |
| 0.2060 每位点的替换数<br />
| |
| coxI <math display="inline">=245.2</math> 百万年 / 2 <math display="inline">\times</math> 0.00042 每百万年每位点的替换数<br />
| |
| 0.4439 每位点的替换数<br />
| |
| atp9 <math display="inline">=193.8</math> 百万年 / 2 <math display="inline">\times</math> 0.001145 每百万年每位点的替换数<br />
| |
| 0.1101 每位点的替换数<br />
| |
| nad4 <math display="inline">=173.1</math> 百万年 / 2 <math display="inline">\times</math> 0.000318 每百万年每位点的替换数
| |
|
| |
| 分母中的因子2源于分化过程中两条谱系独立积累替换。由于不同位点的分子钟速率存在细微差异,估计的分化时间显然依赖于所选位点。这三个位点的平均分化时间(2.04亿年前)与已有数据(Laroche和Bousquet 1995)约2亿年的平均结果一致。
| |
|
| |
| = 习题框8.2答案 =
| |
|
| |
| 马约特与欧洲群体在runt位点各含15条序列样本,故<math display="inline">n=15</math>
| |
|
| |
| <math display="block">
| |
| a_{1}=\sum_{k=1}^{n-1}{\frac{1}{k}}=\sum{\Bigg(}{\frac{1}{1}}+{\frac{1}{2}}+{\frac{1}{3}}+{\frac{1}{4}}+{\frac{1}{5}}+{\frac{1}{6}}+{\frac{1}{7}}+{\frac{1}{8}}+{\frac{1}{9}}+{\frac{1}{10}}+{\frac{1}{11}}+{\frac{1}{12}}+{\frac{1}{13}}+{\frac{1}{14}}{\Bigg)}
| |
| </math>
| |
|
| |
| 且
| |
|
| |
| <math display="block">
| |
| e_{1}=\frac{n+1}{3a_{1}(n-1)}-\frac{1}{a_{1}^{2}}=\frac{15+1}{3(3.2516)(15-1)}-\frac{1}{3.2516^{2}}=-0.02258
| |
| </math>
| |
|
| |
| 接着,
| |
|
| |
| <math display="block">
| |
| a_{2}=\sum_{k=1}^{n-1}{\frac{1}{k^{2}}}=\sum\left({\frac{1}{1^{2}}}+{\frac{1}{2^{2}}}+{\frac{1}{3^{2}}}+{\frac{1}{4^{2}}}+{\frac{1}{5^{2}}}+{\frac{1}{6^{2}}}+{\frac{1}{7^{2}}}+{\frac{1}{8^{2}}}+{\frac{1}{9^{2}}}+{\frac{1}{10^{2}}}+{\frac{1}{11^{2}}}+{\frac{1}{12^{2}}}+{\frac{1}{13^{2}}}+{\frac{1}{14^{2}}}\right)
| |
| </math>
| |
|
| |
| <math display="block">
| |
| c={\frac{2{\bigl(}n^{2}+n+3{\bigr)}}{9n{\bigl(}n-1{\bigr)}}}-{\frac{n+2}{a_{1}n}}+{\frac{a_{2}}{a_{1}^{2}}}={\frac{2{\bigl(}15^{2}+15+3{\bigr)}}{9{\bigl(}15{\bigr)}{\bigl(}15-1{\bigr)}}}-{\frac{15+2}{(3.2516)(15)}}+{\frac{0.576}{\bigl(}}15{\bigr)}^{2}
| |
| </math>
| |
|
| |
| 因此
| |
|
| |
| <math display="block">
| |
| e_{2}={\frac{c}{a_{1}^{2}+a_{2}}}={\frac{0.04813}{3.2516^{2}+1.576}}=0.00396
| |
| </math>
| |
|
| |
| 在欧洲群体(European population)中,556个位点中有17个分离位点(segregating sites),因此
| |
|
| |
| <math display="block">
| |
| \hat{\theta}_{5}=\frac{p_{5}}{a_{1}}=\frac{{17/556}}{3.2516}=0.0094
| |
| </math>
| |
|
| |
| 而在马约特群体(Mayotte population)中,538个位点中有34个分离位点,因此
| |
|
| |
| <math display="block">
| |
| \hat{\theta}_{5}=\frac{5}{a_{1}}=\frac{34/538}{3.2516}=0.0194
| |
| </math>
| |
|
| |
| 欧洲群体的Tajima’s <math display="inline">D</math>值为
| |
|
| |
| <math display="block">
| |
| \begin{array}{c}{{D=\displaystyle\frac{\hat{\theta}_{\pi}-\hat{\theta}_{\ S}}{\sqrt{e_{1}p_{S}+e_{2}p_{S}\left(p_{S}-1\right)}}=\displaystyle\frac{0.0124-0.0094}{\sqrt{(0.0226)0.0306+(0.00396)(0.0306)(0.0306-1)}}}\ {{\displaystyle=0.0030/0.02393=0.1254}}\end{array}
| |
| </math>
| |
|
| |
| 而马约特群体的Tajima’s <math display="inline">D</math>值为
| |
|
| |
| <math display="block">
| |
| \begin{array}{l}{{D={\frac{{\hat{\theta}}_{\pi}-{\hat{\theta}}_{S}}{\sqrt{{e_{1}p_{S}}+{e_{2}p_{S}}({p_{S}}-1)}}}={\frac{0.0135-0.0194}{\sqrt{(0.0226)(0.0632)+(0.00396)(0.0632)(0.0632-1)}}}}\ {{\mathrm{}}}\ {{\mathrm{}={\vphantom{\frac{{\pi}}{{\sqrt{{e_{1}p_{S}}+{e_{2}p_{S}}({p_{S}}-1)}}}}}-0.0059/0.0345=-0.0171.}}\end{array}
| |
| </math>
| |
|
| |
| 两个群体的DNA序列多态性模式均未偏离标准中性模型(standard neutral model)的预期。
| |
第4章
种群结构与基因流
4.1 遗传种群
种群的遗传组织与地理组织。
距离隔离【“Isolation by distance”译为“距离隔离”】与其他遗传隔离模型。
基因流与迁移。
第2章详细讨论的基因型以Hardy–Weinberg频率存在的预期,依赖于整个种群随机交配的假设。这一观点隐含了种群作为单一实体的前提——其中交配和个体迁移等过程在整个种群中均匀发生,这种状态常称为泛交(panmixia)。然而,实际种群中起作用的若干过程和特征使得这种种群均质化的初始视角难以适用于多数种群。在大型种群中,交配机会往往不符合Hardy–Weinberg假设的均质分布。相反,两个个体交配的概率常取决于它们在种群内的空间位置。这种现象导致了所谓的种群结构——即整个种群中随机选取的两个个体交配概率存在异质性。本章第一节将介绍导致交配与迁移过程中种群结构的生物学现象,这些现象可能引起种群不同区域的等位基因和基因型频率差异。全章的目标是建立种群结构对基因型和等位基因频率影响的预期,并提出测量种群结构模式的方法。
为初步理解种群如何被划分为独立运作的亚单元,请考虑某个假想种群:
图 4.1. 最初,种群中所有个体无论其位置如何都有均等的交配机会。由于交配是随机的,整个种群的基因型频率符合哈迪-温伯格预期,且溪流两岸的等位基因频率相等。接着,设想将分割种群的溪流永久变为大型河流,成为个体从一侧向另一侧迁移的屏障。尽管偶尔仍有少数个体会穿越河流,但被河流分割的两个亚种群间的基因混合或基因流速率降低了。基因流水平的下降意味着两个亚种群的等位基因频率和基因型频率随时间趋向独立。
在图 4.1 的后续时间点中,两个亚种群的等位基因频率随时间推移因遗传漂变而差异逐渐增大——尽管每个亚种群内部仍保持哈迪-温伯格预期的基因型频率。在图 4.1 的最后时间段,被河流分隔的亚种群的等位基因频率已显著不同,且总种群的基因型频率不再满足哈迪-温伯格预期。此例中,基因流的减少使两个亚种群能独立受遗传漂变作用,最终导致等位基因频率的种群分化。地理屏障的出现会限制种群间的基因流,如图 4.1 所示。亚种群(以兽群、鸟群、狮群、鱼群甚至城市等名称识别的实体)可通过时间、行为及地理屏障等多种方式形成,最终使其等位基因频率偏离总种群的平均等位基因频率。
另一种种群结构的成因更为微妙,但通过思想实验容易理解。试想你在家或工作场所常遇见的一种常见动植物物种。设想该物种个体完全随机寻找配偶,个体可能在何处找到配偶?它们更可能与邻近个体而非远方个体交配。我曾观察过住所附近和工作大学校园中的树木。当这些树木通过花粉传播开花交配时,邻近树木更可能成为配偶。相距数十或数百公里的两棵树很难有机会交配。
设想你思考的物种及其可能发生交配的距离。即使个体能在极远处找到配偶,通常也存在某个空间尺度会限制交配概率。这因物种而异:可能小至数米(取决于个体及其配子的移动范围),也可能大至数千公里。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/f74b56a78f5c6556c755ec317885b6394bad32c4fee23a7e7f992e8905955fdc.jpg
图4.1 由有限基因流产生的种群结构和等位基因频率分化的示例。整个种群(大椭圆形)最初处于随机交配(panmixia)状态,并具有Hardy–Weinberg预期的基因型频率。随后,贯穿种群的溪流发展成一条大河,限制了整个种群两侧之间的基因流。随着时间的推移,两个亚种群中的等位基因频率通过遗传漂变发生分化。在此示例中,可以设想两个亚种群分别漂向不同等位基因的固定,但均未完全固定,因为偶尔有个体能够越过河流并交配。注意,每个亚种群内部仍存在随机交配(panmixia),因此Hardy–Weinberg预期的基因型频率在亚种群内得以维持。然而,在初始时间段后,整个种群的基因型频率不再符合Hardy–Weinberg预期。
这种随个体间距离增加而交配机会减少的现象被称为距离隔离(isolation by distance)(Wright 1943a, b, 1946; Malécot 1969)。Sewall Wright受到植物Linanthus parryae(图4.2)蓝花与白花空间频率数据的启发,为经历距离隔离的种群建立了理论预期。L. parryae花色频率的拼图式空间格局被Wright视为连续种群中距离隔离后果的典型案例。Wright(1978)对L. parryae花色频率数据进行了一系列详细分析。然而,关于花色的遗传基础以及自然选择在野外塑造L. parryae花色空间分布的可能性,争议已持续超过50年(见Schemske与Bierzychudek 2001;Turelli等2001)。尽管L. parryae的具体作用机制尚无定论,距离隔离现象在自然种群中普遍存在。距离隔离可视为自然种群遗传学中的零假设(null hypothesis),核心问题在于其影响基因型和等位基因频率的地理尺度(见Meirmans 2012)。
亚种群之间及内部的基因流动模式可能呈现多种形式,已有多种模型被提出以捕捉这种多样性。例如,“屏障隔离”(isolation by barrier)描述由地理和生境障碍(如图4.1所示的河流)导致的基因流动速率降低现象(Vignieri 2005)。(在系统发育背景下,术语”地理阻隔”(vicariance)常用于描述类似的阻碍迁徙和基因流动并促进物种形成的屏障。)“抗阻隔离”(isolation by resistance, IBR)模型允许基因流动速率存在梯度变化,其名称源于电路中电子流受不同强度电阻器调节的类比(McRae 2006)。IBR可能由生境的空间异质性、基质类型差异(即适宜生境斑块周围个体或配子扩散所穿越的区域),以及基因流动必须跨越的屏障共同导致。
此外,不对称基因流动可能源于”垄断化”(monopolization)现象:当先到拓殖者具有数量优势时,会降低后来迁入者的定殖成功率,从而在亚种群初步建立后减少其间的基因流动(De Meester et al. 2002)。垄断化可能导致”定殖隔离”(isolation by colonization)格局,此时遗传结构反映时间维度上的拓殖历史,遗传分化与地理距离或环境差异之间未必存在关联(Orsini et al. 2013)。“环境隔离”(isolation by environment)指基因流动受阻及其引发的种群遗传分化与地理距离无关,这种隔离可由多种物理屏障和湿度、降水、土壤类型等非生物因子导致(Wang and Bradburd 2014)。环境隔离也可能是”适应隔离”(isolation by adaptation)的结果——当存在强烈自然选择导致局域适应时,迁入者会经历定殖或交配成功率降低,从而引发种群间遗传分化。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/fc6ff724b884d78742953e44a4921548253760219aaa9639a5c6ae52dfc5fa52.jpg
图4.2 沙漠雪花(Linanthus parryae)分布于加利福尼亚州莫哈韦沙漠地区。在降水充足的年份,土壤中休眠种子可大规模萌发,这种植物可覆盖数千公顷荒漠。该小型植物具有蓝花或白花表型:某些区域以蓝花或白花植株为主,另一些区域则呈现更均衡的花色比例。图片来源:Dr. Barbara J. Collins/http://www.clunet.edu/wf.
区分这些及其他可能导致基因流速率和模式的因子,是景观遗传学研究的主要部分。该领域采用种群遗传预测模型、空间明确的基因型和等位基因频率数据、遗传采样点周围的地理信息系统(GIS)数据等空间信息,以及空间统计方法来检验影响基因流和遗传分化的地理过程假说(Balkenhol et al. 2015)。景观遗传学旨在通过基因流识别和检验遗传连通性与不连续性的成因假说,同时检验景观特征与遗传分化模式之间的相关性(Manel et al. 2003)。其中一个重点领域是预测和保护扩散走廊,以维持因自然栖息地变异及农业、聚落和建筑等人为影响而隔离的种群间的基因流。例如,Sharma et al.(2013)发现当代基因流在通过森林走廊连接的遗传分化老虎亚种群间达到最大。
计算机模拟是探索距离隔离如何影响等位基因和基因型频率的便捷方法。图4.3展示两个模拟种群,其中网格上的每个点代表一个二倍体个体的地理位置。在一种情况下,种群呈现随机交配(panmixia),个体在99×99个体的交配区域内随机选择配偶;在对比情况下存在强距离隔离,个体仅在更小的3×3个体区域内随机交配。两个种群初始状态极为相似:
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/d9b29f30d081e7bfa8cf80868156716584f51adbb326a513d10067b2863db2ea.jpg
图4.3 距离隔离导致等位基因和基因型频率的空间结构化。图中二维网格的每个点代表一个二倍体个体,颜色表示每个位点的杂合(蓝色)或纯合(黑/白)基因型。A组显示全种群随机交配(交配邻域为99×99网格),B组显示强距离隔离(交配邻域为3×3网格)。具有距离隔离的种群(B)发展并维持基因型的空间聚集,进而导致等位基因频率的空间聚集,而随机交配种群(A)无此空间结构。模拟初始时,网格中基因型按哈迪-温伯格(Hardy–Weinberg)预期频率随机分布,且p=q=1/2。每代中,个体在其交配邻域内随机选择配偶,并通过一个后代替换自身,子代基因型由亲本基因型的哈迪-温伯格组合概率决定。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/d14ce4a49cc4acc78731d0440bc7bf37f1ff492276b8b7755bc3e8ffc56e7986.jpg
图4.3(续)
哈迪-温伯格(Hardy–Weinberg)预期基因型频率与三种基因型的随机分布格局。经过 200 代后,具有 <math display="inline">99\times99</math> 个体交配区域的种群(图 4.3A)仍显示三种基因型的随机分布。然而,具有 <math display="inline">3\times3</math> 交配区域的种群(图 4.3B)则形成了明显的同基因型集群,且杂合体数量减少。
距离隔离(isolation by distance)的一个明显效应是种群中等位基因频率的局部变化,局部区域趋向固定或丢失,类似于有效种群规模减小的效应(见第 3 章关于繁殖有效种群规模的内容)。或者,距离隔离可视为近亲交配的一种形式,因为受限的交配距离会导致亚种群内纯合性增加。模拟种群中的基因型分布模式印证了这一点——随着距离隔离的持续,杂合体总体频率随时间显著下降(图 4.3B),而在随机交配(panmixia)情况下则无此现象(图 4.3A)。
距离隔离(Isolation by distance):随着个体或种群间地理距离增加,交配或基因流动机会逐渐减少的现象。
基因流(Gene flow):通过个体移动(迁徙)或配子移动,等位基因成功进入种群的过程。
随机交配(Panmixia):字面意为”完全混合”的随机交配方式。
种群结构(Population structure):种群不同部分在等位基因和/或基因型频率上的异质性,通常由空间或时间定义。这种结构模式可由遗传漂变与有限基因流的综合作用,以及自然选择等多种过程形成。
亚种群(Subpopulation):总种群中因基因流受限而使其等位基因频率能在一定程度上独立演化的部分;与繁殖群(deme)同义【“deme”译为“繁殖群”】。
种群结构对基因型和等位基因频率有深远影响。亚群划分将种群分解为若干较小的单元,每个单元在遗传上具有一定程度的独立性。其后果之一是:与随机交配的整个种群相比,每个亚群的有效种群大小更小。单一大型随机交配种群与划分为多个小型繁殖群的种群,其遗传多态性的组织形式存在差异。以双等位基因座为例:单个大型种群可能因遗传漂变而需要极长时间才能达到等位基因的固定或丢失,从而维持两个等位基因;而在高度分化的种群中,每个繁殖群可能快速达到固定或丢失,但整体种群仍可维持两个等位基因——因为对于某个特定等位基因,预计半数亚群会达到固定,半数会丢失。导致种群结构的过程也可视为进化改变的创造性与限制性并存(Slatkin 1987a)。亚群间的遗传隔离可阻止新等位基因(包括有利等位基因)在种群中扩散;但与此同时,遗传隔离允许亚群形成独立的等位基因频率,并维持独特等位基因,这正是自然选择下遗传适应局域环境所必需的条件。
值得注意的是,基因流与迁移(migration)或扩散(dispersal)存在重要生物学区别。迁移(或扩散)仅指个体从一个地点到另一个地点的移动行为,这种移动未必导致基因流。基因流要求迁移个体能成功将其等位基因贡献至迁入种群的交配池。因此,单纯迁移未必引发基因流。同理,基因流也可不依赖个体迁移而发生。植物是典型例证:其基因流通过花粉粒(雄配子)移动实现,而个体(除种子阶段外)无法迁移。基因流也可在个体迁移不易察觉的情况下发生,例如个体短暂移动交配后返回原栖息地。容易混淆的是,变量<math display="inline">m</math>(迁移率)在种群结构模型中几乎普遍用于表示基因流速率。尽管模型通常不作区分,但需谨记实际种群中迁移过程与基因流过程的生物学差异。
Box 4.1 二维空间中等位频率呈随机分布还是聚集分布?
如何描述遗传变异的空间分布,以寻找距离隔离或其他导致种群空间遗传分化的证据?通用方法是比较个体对或种群对,同时考察其基因型相似度与空间距离。距离隔离是由非随机交配导致的亲缘交配形式,它使得空间邻近的个体平均具有更高的亲缘关系。
用于估计空间遗传结构的一种经典统计量是称为Moran’s I的相关性度量:
<math display="block">
I_{k}=\frac{\displaystyle{n\sum_{i=1}^{n}\sum_{j=1(i\neq j)}^{n}w_{i j}\big(\gamma_{i}-\overline{{{\gamma}}}\big)\left(\gamma_{j}-\overline{{{\gamma}}}\right)}}{\displaystyle{W_{k}\sum_{i=1}^{n}\big(\gamma_{i}-\overline{{{\gamma}}}\big)^{2}}}
</math>
其中<math display="inline">k</math>代表距离类别(例如相隔两个距离单位的所有种群),因此当位置<math display="inline">i</math>和<math display="inline">j</math>之间的距离等于<math display="inline">k</math>时<math display="inline">W_{j j}</math>为1,否则为0。在距离类别<math display="inline">k</math>内,<math display="inline">n</math>是种群数量,<math display="inline">y</math>是遗传变量(如位置<math display="inline">i</math>或<math display="inline">j</math>的等位基因频率)的值,<math display="inline">\overline模板:Y</math>是所有种群的平均等位基因频率,<math display="inline">W_{k}</math>是权重<math display="inline">W_{j j}</math>之和或<math display="inline">2n k</math>。当种群对的等位基因频率相似且与平均等位基因频率差异较大时,分子会更大。
与一般相关性类似,当使用大量样本估计时,Moran’s I的取值范围为<math display="inline">-1</math>到<math display="inline">+1</math>。<math display="inline">I</math>的正值意味着位置对之间的等位基因频率在平均意义上相似,而负值意味着位置对之间的等位基因频率在平均意义上倾向于不同。值为0表示亚种群等位基因频率的差异与位置间距离无关,或遗传变异在空间上随机分布。如图4.3所示的基因型空间位置是使用Moran’s I的理想场景(见图4.4)。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/d81aebf7bda30986a41a9f6000012e70abe9c2276375ce5c8102037c7219c9a9.jpg
图4.4 模拟种群(类似图4.3)的Moran’s I。为估计Moran’s I,对100×100网格进行了200代的模拟,然后将其划分为10×10个体的方形亚种群。每个亚种群内A allele的频率为<math display="inline">y_{i}</math>,而所有亚种群的平均等位基因频率为式4.1中的<math display="inline">\overline模板:Y</math>。距离类别是分隔亚种群对的亚种群数量。正如预期,具有强距离隔离(3×3交配邻域)的模拟显示相邻亚种群间存在等位基因频率相关性。然而,完全随机交配(99×99交配邻域)的模拟显示没有这种等位基因频率的空间相关性。两图中最大距离类别处I的波动是由于比较个体数量极少导致的随机变异。每条线均基于100×100种群的独立模拟。
4.2 基因流及其对多亚种群等位基因频率的影响
基因流模型
大陆-岛屿模型
两岛屿模型
扩散核
基因流是一种混合过程,当单独作用时,最终会使所有亚种群的等位基因频率趋于均质化。在自然种群中,基因流可以呈现多种模式,通过个体或配子的交换将亚种群相互连接。种群遗传学中已广泛研究了一系列基因流模型,这些模型作为重要的参考基准。其中部分基因流模型如图4.5所示。实际生物亚种群内部和之间的基因流可能不像这些模型假设的那样容易分类或恒定不变。尽管如此,这些模型仍然是表征亚种群间基因流可能模式的有用案例。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/32512eb28d47ad746ef8b44a5ed9d2027282e5c03eff93252970b94939783350.jpg
本章第一节介绍了基因流,并展示了有限基因流如何影响等位基因和基因型频率,形成遗传亚种群的潜力。4.2节将介绍基因流模型,展示基因流如何随时间影响等位基因频率。4.3节将引入通过遗传标记确定亲缘关系来直接测量基因流的方法。4.4节将重提第二章的固定指数(或F.),并针对结构化种群的情况进行扩展以量化种群分化模式。4.5节将展示基因型频率变异如何以杂合度形式存在于种群内部,或以等位基因频率差异形式存在于种群间。4.6节将提出理想化种群模型,通过基因流和遗传漂变速率预测遗传分化模式,这些模型可作为估算历史基因流的方法。4.7节介绍最大似然法和贝叶斯法对个体进行遗传种群分类。本章最后一节将种群亚结构整合到溯祖模型中。
图 4.5 种群结构模型对亚种群间基因流的路径和速率作出不同假设。“大陆-岛屿”模型(A)中,基因流是单向的,因为大陆种群规模极大使得其等位基因频率不受迁出或漂变影响,而小种群的等位基因频率则受迁入强烈影响。“岛屿”模型(B)假设所有种群间无论数量或地理位置都以相同速率双向交换基因流(岛屿模型也可调整种群数量从两个到无限个)。“踏脚石”模型将基因流限制于相邻或邻近种群,在一维(C)或二维(D)空间中体现距离隔离效应。“层级岛屿”模型(E)在种群组织的多个层级上设置不同基因流速率(Slatkin 和 Voelm 1991),图示为同一区域内繁殖群间和区域间存在不同基因流速率。“阻力隔离”模型考虑不同繁殖群对间的基因流速率可能因景观阻隔而异,从而影响迁徙(McRae 2006)。基因流模型还可纳入整个亚种群的灭绝与重建过程,这一特征常被添加到踏脚石模型中。各面板箭头所示基因流速率为:若每代种群中迁入个体占比m,则<math display="inline">1{-}m</math>为未迁徙个体占比。
基因流模型的目标是预测遗传混合过程如何随时间影响亚种群的等位基因频率。此类预测的有效起点是假设仅有基因流作用——无遗传漂变、自然选择和突变——进而聚焦于特定基因流模型中基因流的作用方式和速率。本节将详细阐述两种基因流模型中观察到的等位基因频率随时间变化效应。
Continent-island model
或许最简单的基因流模型是”大陆-岛屿”模型(图 4.5A)。该模型假设存在一个极大的种群(其等位基因频率在短期内变化极小)和一个小型种群(每代接受来自大陆种群的迁入者)。岛屿种群每代通过迁徙替换比例为<math display="inline">m</math>的个体,保留<math display="inline">1-m</math>的原有个体(假设岛屿种群每代被替换的m比例个体或死亡或迁回大陆种群,而大陆种群规模极大以致迁入者不会影响其等位基因频率)。
Continent-island model: 一种理想化的种群细分与基因流模型,假设存在一个极大种群(其等位基因频率随时间保持恒定,如个体数量庞大的种群)与一个小种群(每代个体中迁入者占有限比例)通过基因流连接。虽然可能存在从岛屿到大陆的基因流,但假定其对大陆种群等位基因频率的影响可忽略不计。
基于上述情况及其假设,可以预测基因流如何在一代时间内改变岛屿种群中双等位基因位点的等位基因频率。岛屿种群未来一代的等位基因频率(记为<math display="inline">p_{t+1}^{island}</math>)是以下两个因素的函数:(i) 未迁移个体在岛屿种群中所占比例的等位基因频率,以及(ii) 通过基因流从大陆种群迁入岛屿种群的个体所占比例的等位基因频率。这可以用方程表示为
<math display="block">
p_{t=1}^{island}=p_{t=0}^{island}(1-m)+p^{continent}m
</math>
并用于预测经过一代基因流后岛屿种群的等位基因频率。展开该方程右侧可得
<math display="block">
p_{t=1}^{island}=p_{t=0}^{island}-p_{t=0}^{island}m+p^{continent}m
</math>
将其重新排列后可得到一个描述岛屿种群等位基因频率在一代时间内变化的方程
<math display="block">
p_{t=1}^{island}-p_{t=0}^{island}=-m\left(p_{t=0}^{island}-p^{continent}\right)
</math>
该形式便于生物学解释。
方程4.41预测,只要基因流速率不为0(<math display="inline">m\neq0</math>),岛屿与大陆种群间等位基因频率的差异程度(<math display="inline">p_{t=0}^{island}-p^{continent}</math>)将决定岛屿等位基因频率变化的方向和速率。例如,若<math display="inline">p_{t=0}^{island}>p^{continent}</math>,则岛屿等位基因频率应下降;同理,若<math display="inline">p_{t=0}^{island}<p^{continent}</math>,则岛屿等位基因频率应上升。以数值为例,假设<math display="inline">p_{t=0}^{island}=0.1</math>且<math display="inline">p^{continent}=0.9</math>,岛屿与大陆等位基因频率差异为<math display="inline">-0.8</math>,根据方程4.41,任何程度的基因流都将导致岛屿等位基因频率上升。若<math display="inline">m=0.1</math>,则岛屿等位基因频率在一代内将增加0.08至<math display="inline">p_{t=1}^{island}=0.18</math>。
单代基因流引起的等位基因频率变化预期还可扩展用于预测任意代数的岛屿种群等位基因频率。若存在第二代基因流,则岛屿种群的等位基因频率为
<math display="block">
p_{t=2}^{island}=p_{t=1}^{island}(1-m)+p^{continent}m
</math>
将方程4.41定义的<math display="inline">p_{t=1}^{island}</math>代入得
<math display="block">
p_{t=2}^{island}=\big(p_{t=0}^{island}(1-m)+p^{continent}m\big)(1-m)+p^{continent}m
</math>
将其重新排列为
<math display="block">
p_{t=2}^{island}=p_{t=0}^{island}(1-m)^{2}+p^{continent}(m(1-m)+m)
</math>
最终可得两代基因流后岛屿等位基因频率(<math display="inline">p_{t=2}^{island}</math>)相对于初始频率(<math display="inline">p_{t=0}^{island}</math>)的预期表达式
<math display="block">
p_{t=2}^{island}=p_{t=0}^{island}{(1-m)}^{2}+p^{continent}{\left(1-{\left(1-m\right)}^{2}\right)}
</math>
通过归纳可得通用表达式
<math display="block">
p_{t}^{island}=p^{continent}+\left(p_{t=0}^{island}-p^{continent}\right)\left(1-m\right)^{t}
</math>
或等价形式
<math display="block">
p_{t}^{island}=p_{t=0}^{island}(1-m)^{t}+p^{continent}\bigl(1-(1-m)^{t}\bigr)
</math>
注意,指数等于经过的世代数。将这些指数改为任意数,即可得到从初始等位基因频率开始经过<math display="inline">t</math>世代后岛屿种群的等位基因频率:
岛屿种群中等位基因频率的变化速率也可从此方程中看出。构成其初始等位基因频率的岛屿种群比例以<math display="inline">{(1-m)}^{t}</math>递减,由于基因流的存在,随着时间的推移逐渐趋近于零。因此,岛屿与大陆之间的等位基因差异随时间推移逐渐减小至0,岛屿的等位基因频率趋近于大陆的等位基因频率。图4.6展示了在不同初始岛屿等位基因频率下,岛屿等位基因频率随时间趋近大陆等位基因频率的过程。注意其平滑趋近大陆等位基因频率的特征:这反映了结果完全由恒定的基因流速率决定,而缺乏引入随机变异(如遗传漂变)的随机过程。在实际种群中,基因流速率本身可能随时间随机波动。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/7442d6ea9e209a982a7e374b43795c2e841e80320a6ed9650512d03a07b17044.jpg
图4.6 大陆-岛屿基因流模型下双等位基因位点在岛屿种群中的等位基因频率。展示了六个不同初始值(实线)对应的岛屿种群等位基因频率<math display="inline">({p}^{island})</math>随时间变化。大陆种群等位基因频率为<math display="inline">p^{continent}=0.5</math>(虚线)。左图<math display="inline">m=0.1</math>,右图<math display="inline">m=0.05</math>。当基因流速率较低时,达到平衡更慢。相比之下,对于给定基因流速率,岛屿与大陆间等位基因频率差异不影响达到平衡的时间。注意两图时间尺度不同。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/868f684aaa6becde7cb9551efc73d80a0eb5f1f70079f6ea84a03c13695ddb14.jpg
图4.7 双岛屿基因流模型中双等位基因位点的等位基因频率。初始等位基因频率为0.9和0.2,基因流速率相等<math display="inline">(m=0.1)</math>时,亚种群趋近于平衡等位基因频率<math display="inline">\bar{p}=0.5</math>(虚线)。当两个亚种群初始等位基因频率相同但基因流速率不对称时(<math display="inline">m_{1}=0.1</math>和<math display="inline">m_{2}=0.05</math>),亚种群趋近于平衡等位基因频率<math display="inline">\overline{p}=0.433</math>(虚线)。基因流速率不对称时,由于一个种群的基因流速率较低,达到平衡更慢。注意两图时间尺度不同。
这些对大陆-岛屿模型的预测与直觉一致。由于大陆种群随时间保持恒定的等位基因频率,当两者混合时,岛屿种群最终应达到相同的等位基因频率。两个种群趋同于相同等位基因频率所需的时间取决于每代从大陆迁移到岛屿的个体比例。相反,岛屿与大陆之间等位基因频率的差异不会改变给定迁移率下的平衡时间(见图4.7)。这是因为岛屿等位基因频率的变化速率由等位基因频率的差异决定。差异越大,朝向大陆等位基因频率的变化速率越快。因此,大陆-岛屿模型表明,仅基因流过程就足以使种群达到相同的等位基因频率。种群间或种群内等位基因频率的完全一致实际上意味着缺乏种群结构或达到panmixia。因此,大陆-岛屿模型可以视为证明:在没有其他过程作用时,基因流最终将导致panmixia。
双岛屿模型
对大陆-岛屿模型的一个简单扩展是将两个亚种群视为大小相等,从而消除一个种群(大陆)作为不变迁移源的假设。该模型表示两个岛屿间的基因流,每个岛屿的等位基因频率均可随时间变化。转变为
互动框4.1 大陆-岛屿基因流模型
使用R脚本探索大陆-岛屿基因流模型。脚本包含岛屿和大陆的等位基因频率、岛屿等位基因被大陆等位基因替换的速率(或迁移率),以及模拟的世代数。初始设定大陆等位基因频率为0.9,岛屿为0.1,基因流速率0.1,模拟100代。保持初始等位基因频率不变,尝试一系列迁移率值(如<math display="inline">m=0.1</math>、0.05、0.001和0.001),观察其对平衡时间的影响;必要时增加世代数。
基因流速与平衡时间的关系如何?
双岛屿模型也允许每个亚种群有独立的基因流速率<math display="inline">m_{1}</math>和<math display="inline">m_{2}</math>。通过类似大陆-岛屿模型的推理,一个亚种群在未来一代的等位基因频率是不迁移个体比例<math display="inline">(1-m)</math>的等位基因频率与移民等位基因频率的加权和。假设<math display="inline">m_{1}=m_{2}=m</math>,则任一亚种群的等位基因频率为
<math display="block">
p_{t=1}=p_{t=0}(1-m)+\overline模板:Pm
</math>
其中<math display="inline">\overline模板:P=\frac{p_{1}+p_{2}}{2}</math>。移民的等位基因频率现在是两个亚种群的平均值,而非如大陆模型中的恒定值。这是因为两个亚种群均接收移民,因此基因流混合亚种群时,每个亚种群的等位基因频率逐渐趋近于总种群的等位基因频率。与大陆-岛屿模型的结果类似,两个岛屿中任一岛屿的等位基因频率为
<math display="block">
p_{t}=\overline模板:P+\big(p_{t=0}-\overline模板:P\big)\big(1-m\big)^{t}
</math>
经过<math display="inline">t</math>代后,等位基因频率的变化如图4.7所示的双岛模型随时间变化趋势。
当基因流速率不相等时,平均等位基因频率为<math display="inline">\overline模板:P = \frac{m_{2}}{m_{1}+m_{2}}p_{1} + \frac{m_{1}}{m_{1}+m_{2}}p_{2}</math>,即两个亚种群等位基因频率的基因流加权平均值。当<math display="inline">m_{1}\neq m_{2}</math>时,平衡状态下的等位基因频率会更接近迁移率较低亚种群的初始等位基因频率。这是因为迁移率较低的亚种群接收的迁入个体较少,更接近其初始等位基因频率,同时仍会向另一个亚种群输出迁出个体。如图4.14所示,当迁移率不对称时,达到平衡所需的时间也更长。考虑迁移率不等(<math display="inline">m_{1}=0.01</math>和<math display="inline">m_{2}=0.1</math>)且两个亚种群初始等位基因频率分别为<math display="inline">p_{1}=0.9</math>和<math display="inline">p_{2}=0.1</math>的案例,此时加权平均等位基因频率为<math display="inline">\overline模板:P=\frac{(0.9)(0.1)}{0.11}+\frac{(0.1)(0.01)}{0.11}=0.827</math>,这也是平衡时两个亚种群共同的预期等位基因频率。
双岛模型的主要结论是:当两个亚种群间迁移率相等时,其平衡等位基因频率等于总种群的平均等位基因频率。该结论在亚种群数量更多时依然成立,这一结果对于理解岛屿模型中基因流与遗传漂变等其他过程共同作用时具有重要意义。
无论是大陆-岛屿模型还是双岛模型,都未考虑距离隔离效应。通过将基因流速率表达为距离的函数,可以建立亚种群间距离与基因流速率的定量关系。个体出生地与繁殖地之间的直线(欧几里得)空间距离概率分布称为扩散核(Nathan等学者2012年综述)。扩散核函数可呈现多种形式,图4.8展示了若干示例。某些扩散核(如gamma分布)因短距离密度依赖性而表现出中程基因流概率最高(图4.6B)。其他扩散核因基因流概率随距离下降速率较慢,被描述为“厚尾”或尖峰态【“leptokurtic”译为“尖峰态”】。自然种群中扩散核的经验估计显示……
交互框4.2 基因流的双岛模型
通过R脚本探索基因流的双岛模型。脚本包含各岛屿初始等位基因频率、基因流速率和模拟世代数的变量。初始参数建议设置为:大陆等位基因频率0.9,岛屿等位基因频率0.1,基因流速率为0.1,模拟100代。
保持初始等位基因频率不变,尝试不同迁移率参数(如<math display="inline">m=0.1</math>、0.05、0.001和0.001)并观察其对平衡时间的影响,必要时增加模拟世代数。
基因流速率与达到平衡的时间之间存在何种关系?
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/74979ce11e287ad880ab7bd6fa61d0b9525cc758bd06b32bdcf6c8d57e751cc3.jpg
图 4.8 展示扩散事件在空间距离上概率分布的扩散核概率分布。与A和D相比,B和C中的分布具有肥尾特征,而D的分布尾部最薄。图A显示均值为零、方差为1的半正态分布。图B是尺度参数为2、形状参数为1的伽马分布。图C是尺度参数为2、形状参数为1的威布尔分布。图D是参数为<math display="inline">a=0.55</math>和<math display="inline">b=1.8</math>的2Dt分布。
对自然种群的研究表明,扩散过程通常最适合用某种类型的尖峰分布(leptokurtic distribution)描述。尽管基因流距离分布的具体形态会影响遗传分化的程度和空间尺度,但血缘同一性随距离递减的整体趋势并不强烈依赖于这种分布的精确形状(Rousset 2008a; Furnstenau and Cartwight 2016)。
4.3 基因流的直接测量方法
基于遗传标记的亲本分析。
本节将介绍如何利用分子遗传标记识别子代样本中未知的父本或母本,从而解析亲本间的交配模式。亲本分析被认为是基因流的直接测量方法,因为它们能揭示候选亲本采样尺度内的配子移动模式。这类分析也常被用于检验影响个体间交配模式的因素假说。例如,动物亲本研究可检验交配成功率与表型或行为特征的相关性。亲本分析通常应用于已知一方亲本而另一方未知的情况,此时未知亲本可能是候选亲本群体中的任意个体。试图从候选亲本群体中识别未知父本或母本的遗传分析分别称为父权分析(paternity analysis)或母权分析(maternity analysis)(参见Meagher 1986; Devlin and Ellstrand 1990; Dow and Ashley 1996; Jones et al. 2010综述)。虽然本文不展开讨论,但也可通过推断候选亲本群体中双亲未知的情况来估计贡献于子代群体的最少亲本数量。本节将通过父权分析案例,概述理解亲本分析方法与结果所需的基本概念,重点区分真实亲本鉴定与因随机匹配而被误判为亲本的候选个体间的差异。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/26542602d0dec0e004fb1caef35edd09089fde2bab6ae2ad1acd3dbf7a0fcb6c.jpg
图4.9 发现于巴西亚马逊北部森林碎片生物动态研究项目(Biological Dynamics of Forest Fragments Project)野外站点的Corythophora alta个体。地图显示了位于Cabo Frio的9公顷森林样地内构成候选亲本种群的所有个体树木的相对位置。由于这些树木是能够自交的两性体,所有个体均可同时作为母本和候选父本。
为了理解亲本分析的实施步骤,让我们通过一个基于热带树种Corythophora alta(巴西坚果科成员,见图4.9)基因型数据的案例进行说明。所有胸高直径≥10 cm的C. alta个体均从大片连续森林内的9公顷区域中取样。这些胸高直径≥10 cm的树木即为候选亲本。同时从部分树木上采集了种子样本。对树木和种子的10个核微卫星位点(关于此类遗传标记的简介见专栏2.1)进行了基因型分型。表4.1展示了部分数据。本案例中亲本分析的目标是通过已知母本确定种子的父本,以评估样地内花粉传播与样地外花粉传播所产生种子的比例。
亲本分析的第一步是检测子代个体与已知亲本的等位基因匹配情况。表4.2中将C. alta种子的基因型与其已知亲本归类展示。例如表4.2中,来自989号树的种子1-1基因型列于首行,已知母本(989号树)的基因型列于次行。在每个位点上,子代基因型中均能观察到已知亲本基因型的一个(或有时两个)等位基因。对于989号树的种子1-1,已知亲本在位点A贡献了336等位基因,位点B的106等位基因,位点C的165等位基因,位点D的275等位基因,以及位点E的153等位基因。由于这些等位基因来自已知亲本,真实父本必须在位点A至E分别贡献327、91、185、287和153等位基因。这种在二倍体位点上由单个等位基因构成的集合称为父本单倍型。此时可扫描候选亲本的基因型,寻找是否有个体携带包含所有这些等位基因的单倍型(通常借助计算机程序完成)。所有具有匹配单倍型的候选亲本均可能成为989号树种子1-1的父本。本例中,1946号树是唯一符合要求的个体,因此1946号树可能是其父本,而其他候选亲本均因父本单倍型中一个或多个位点的遗传不匹配而被排除。
排除潜在亲本的过程还需考虑基因分型中可能的方法学误差、聚合酶链式反应(PCR)中未扩增的等位基因(称为无效等位基因),或由突变引起的亲本与子代间等位基因状态变化(Sancristobal与
表 4.1 热带树种Corythophora alta的30个成熟个体在9公顷连续森林样地(位于巴西亚马逊)中采集的微卫星基因型数据,等位基因状态以碱基对表示。种子后代采自已知母树。缺失数据以”—“表示。
| Microsatellite locus |
|------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| A | B | C | D | E |
|---------------|--------|--------|--------|--------|
| Candidate parents 684 | 333 | 339 | 97 | 106 | 169 | 177 | 275 | 305 | 135 | 135 |
| 989 | 330 | 336 | 97 | 106 | 165 | 181 | 275 | 275 | 135 | 153 |
| 1072 | 315 | 333 | 103 | 106 | 169 | 179 | 296 | 302 | 138 | 138 |
| 1588 | 318 | 327 | 106 | 106 | 165 | 167 | 272 | 293 | 135 | 150 |
| 1667 | 324 | 333 | | | 165 | 185 | 275 | 284 | 141 | 159 |
| 1704 | 318 | 327 | 103 | 106 | | | 284 | 296 | 144 | 147 |
| 1836 | 333 | 339 | 97 | 97 | 181 | 183 | 275 | 296 | 138 | 144 |
| 1946 | 327 | 333 | 91 | 106 | 167 | 185 | 284 | 287 | 147 | 153 |
| 2001 | 321 | 336 | | | 177 | 181 | 284 | 302 | 138 | 144 |
| 2121 | 318 | 333 | 100 | 106 | 179 | 181 | 284 | 302 | 144 | 144 |
| 2395 | 327 | 333 | 103 | 103 | 179 | 187 | 275 | 296 | 150 | 159 |
| 3001 | 324 | 333 | 91 | 106 | 167 | 183 | 284 | 302 | 147 | 159 |
| 3226 | 327 | 327 | 103 | 106 | 163 | 181 | 275 | 275 | 135 | 144 |
| 3237 | 324 | 324 | 91 | 103 | 179 | 187 | 284 | 305 | 144 | 159 |
| 3547 | 321 | 321 | 103 | 106 | 177 | 179 | 275 | 296 | | |
| 4112 | 327 | 327 | 97 | 106 | 169 | 181 | 296 | 302 | 144 | 144 |
| 4783 | 321 | 327 | | | 183 | 185 | 290 | 308 | 144 | 156 |
| 4813 | 327 | 333 | 106 | 106 | 177 | 179 | 284 | 302 | 135 | 138 |
| 4865 | 321 | 327 | 106 | 106 | 167 | 179 | 284 | 296 | 144 | 153 |
| 4896 | 315 | 333 | 100 | 106 | 181 | 189 | 275 | 284 | 162 | 162 |
| 5024 | 318 | 327 | 100 | 103 | 165 | 167 | 275 | 284 | 147 | 147 |
| Seed progeny |
|----------------------------------|
| 989 seed 1-1 | 327 | 336 | 91 | 106 | 165 | 185 181 | 275 275 | 287 | 153 | 153 135 |
| 989 seed 2-1 | 327 | 330 336 | 103 97 | 106 106 | 165 165 | 181 | | 275 | 135 135 | 153 |
| 989 seed 3-1 | 330 | | | | 167 | 181 | 275 | 296 | | 153 |
| 989 seed 25-1 | 321 | 330 | 106 | 106 | | | | | 135 | |
表 4.2 已知母本基因型及所有可能候选亲本中最可能父本基因型对应的种子后代基因型。种子后代中与已知母本匹配的等位基因用下划线标注。由于该物种可自花授粉,已知母本也可作为候选父本。缺失数据用”—“表示
|
|
A
|
B
|
C
|
D
|
E
|
| 989seed1-1
|
327
|
336
|
91
|
106
|
165
|
| 989
|
330
|
336
|
97
|
106
|
165
|
| 1946
|
327
|
333
|
91
|
106
|
167
|
| 989seed2-1
|
327
|
330
|
103
|
106
|
165
|
| 989
|
330
|
336
|
97
|
106
|
165
|
| 3226
|
327
|
327
|
103
|
106
|
163
|
| 989seed3-1
|
330
|
336
|
97
|
106
|
165
|
| 989
|
330
|
336
|
97
|
106
|
165
|
| 989
|
330
|
336
|
97
|
106
|
165
|
| 989seed25-1
|
321
|
330
|
106
|
106
|
167
|
| 989
|
330
|
336
|
97
|
106
|
165
|
| 4865
|
321
|
327
|
106
|
106
|
167
|
Chevalet 1997)。候选亲本包括与推断的亲本单倍型完全匹配的个体,以及在某个(或多个)位点存在遗传不匹配的个体。例如表4.2中989号树的seed 2-1,我们可以看到候选亲本1588在B、C和E位点匹配,D位点数据缺失,A位点存在不匹配。若允许单个遗传不匹配,则1588号树仍可作为潜在父本。这种容错亲本分析需要基因分型错误率的经验估计【“genotyping error rates”译为”基因分型错误率”】(Adams et al. 2004;Bonin et al. 2004;Hoffman and Amos 2004)。
除单一候选亲本外排除所有其他候选时,似乎已完成对真实亲本的确定性鉴定。然而,任何未被排除的候选亲本仍有可能并非真实亲本。存在这样一种可能性:某个个体仅凭巧合便拥有与真实亲本相同单倍型的基因型。评估未被排除的候选亲本(有时称为被包含亲本或纳入亲本)并非真实亲本的概率,需确定此类随机匹配的概率。
设匹配单倍型中等位基因的频率为<math display="inline">p_{\mathrm{i}}</math>(其中i表示位点)。在每个位点上,随机匹配的概率即个体在该等位基因上为纯合子(<math display="inline">{p_{\mathrm{i}}}^{2}</math>)或杂合子(<math display="inline">2p_{\mathrm{i}}[1-p_{\mathrm{i}}]</math>)的概率。(在容错分配的情况下,<math display="inline">p_{\mathrm{i}}</math>表示第i位点等位基因分型错误的概率。)因此,单个位点的随机匹配总概率为:
<math display="block">
P({\mathrm{random~match}})=p_{i}^{2}+2p_{i}(1-p_{i})
</math>
该公式基于随机交配与泛交配【panmixia】假设。若亲本分析中使用的所有位点均独立,则给定单倍型所有位点的随机匹配概率为各独立位点随机匹配频率的连乘积,即:
<math display="block">
P({\mathrm{multilocus~random~match}})=\prod_{i=1}^{l o c i}\left(p_{i}^{2}+2p_{i}(1-p_{i})\right)
</math>
其中<math display="inline">\Pi</math>表示对所有位点进行连乘。
回到我们的C. alta案例,我们可以计算每个父系单倍型的随机匹配概率。表4.4列出了单倍型、等位基因频率(见表4.3)、各基因座的随机匹配概率,以及所有五个基因座完全随机匹配的概率。首先关注树1946的单倍型。已知位点A的327等位基因在候选亲本群体中观测频率为0.2703(这是对整个群体等位基因频率的估计),则任何基因型拥有一个该等位基因拷贝的概率为<math display="inline">(0.2703)^{2}+2(0.2703)(1-0.2703)=0.4675</math>。因此我们预计群体中46.75%的个体基因型会携带1或2个327等位基因拷贝。该概率等同于从群体中随机抽取个体(未必包含在候选亲本样本中)能提供正确单倍型作为表4.2种子989 1-1潜在父源的概率。
其他四个位点的随机匹配概率以相同方式计算。我们发现:对于单个位点,能补充已知亲本单倍型并解释种子基因型的基因型预期出现概率在约2%到47%之间。当这些概率在五个位点上累乘时,随机匹配的预期频率将变得极低。如表4.4所示,在随机交配假设下,五个位点完全随机匹配的预期频率介于44/1000到66/1,000,000个基因型之间。这验证了通用原则:通过随机匹配区分真实亲本与表观亲本的能力,既取决于各基因座的等位基因频率,也与可用基因座总数相关。当等位基因频率降低且独立基因座数量增加时,随机匹配概率将减小。
表4.3 用于父权分析的五个Corythophora alta微卫星位点的等位基因频率。
表 4.4 表4.2中包含的父本发生随机匹配的概率。每个位点的随机匹配概率为。单倍型中所有位点的联合随机匹配概率是各独立位点随机匹配概率的乘积。当子代基因型数据缺失时,父本单倍型数据在概率计算中视为缺失$(^{\prime\prime}{-^{\prime\prime}})$。若父本单倍型在某些位点存在多个可能等位基因,则给出最高概率的随机匹配值。各位点的等位基因频率见表4.3。
| 微卫星位点 | | | | | | | | | |
|------------|----|----|----|----|----|----|----|----|----|
| **A** | | **B** | | **C** | | **D** | | **E** | |
| 等位基因 | 频率 | 等位基因 | 频率 | 等位基因 | 频率 | 等位基因 | 频率 | 等位基因 | 频率 |
| 315 | 0.0405 | 91 | 0.0735 | 163 | 0.0217 | 272 | 0.0238 | 135 | 0.2917 |
| 318 | 0.0541 | 97 | 0.3088 | 165 | 0.2283 | 275 | 0.4167 | 138 | 0.0625 |
| 321 | 0.1216 | 100 | 0.0735 | 167 | 0.0761 | 281 | 0.0357 | 141 | 0.0313 |
| 324 | 0.0541 | 103 | 0.1471 | 169 | 0.0435 | 284 | 0.1429 | 144 | 0.2188 |
| 327 | 0.2703 | 106 | 0.3971 | 171 | 0.0217 | 287 | 0.0119 | 147 | 0.0625 |
| 330 | 0.1892 | | | 177 | 0.0543 | 290 | 0.0119 | 150 | 0.0938 |
| 333 | 0.1216 | | | 179 | 0.1304 | 293 | 0.0238 | 153 | 0.1250 |
| 336 | 0.1216 | | | 181 | 0.2065 | 296 | 0.1905 | 156 | 0.0208 |
| 339 | 0.0270 | | | 183 | 0.0652 | 299 | 0.0119 | 159 | 0.0521 |
| | | | | 185 | 0.0435 | 302 | 0.0833 | 162 | 0.0417 |
| | | | | 187 | 0.0326 | 305 | 0.0357 | | |
| | | | | 189 | 0.0109 | 308 | 0.0119 | | |
| | | | | 193 | 0.0109 | | | | |
| | | | | 197 | 0.0543 | | | | |
| Includedfather | Microsatellite haplotype | | | | C | | | E | P(multilocus random match) |
|----------------|---------------------------|---|---|---|-----|---|---|---|----------------------------|
| | A | | | | | | | E | |
| 1946 (seed 1-1) | 327 | | | | 185 | 287 | 135 | | |
| allele frequencies | 0.2703 | | 0.0735 | | 0.0435 | 0.0119 | 0.2917 | | |
| P(random match) | 0.4675 | | 0.1416 | | 0.0851 | | 0.0237 0.4983 | | 0.0000665 |
| 3226 (seed 2-1) | 327 | | 103 | 106 | 181 | 275 | 135 | | |
| allele frequencies | 0.2703 | | 0.0735 | 0.3971 | 0.2065 | | 0.4167 0.2917 | | |
| P(random match) | 0.4675 | | 0.1416 | 0.6365 | 0.3704 | 0.6598 | 0.4983 | | ≤0.03624 |
| 989 (seed 3-1) | 330 | 336 | 97 | 106 | 165 | | 135 | 153 | |
| allele frequencies | 0.1892 | 0.1216 | 0.3088 | 0.3971 | 0.2283 | 0.2065 1.0 | 0.2917 | 0.1250 | |
| P(random match) | 0.3426 | 0.2284 | 0.5222 | 0.6365 | 0.4045 | 0.3704 1.0 | 0.4983 | 0.2344 | ≤0.0440 |
**Candidate parent**: An individual in the pool of possible parents that shares one or both alleles found in an offspring genotype at all loci.
**Cryptic gene flow**: Gene flow events incorrectly assigned to candidate parents but actually due to unobserved parents outside the area where candidate parents were sampled, leading to an underestimate of gene flow distances.
**Exclusion**: Rejection of an individual as a possible parent due to genetic mismatch (neither allele in the individual’s genotype is identical to one of the alleles in the progeny genotype).
**Exclusion probability**: The chance that an individual can be rejected as a candidate parent due to genetic mismatch; depends on allele frequencies and increases with the number of loci and the numbers of alleles per locus employed in a parentage analysis.
We can express the probability that an individual taken at random from a population would be ruled out as a parent due to genetic mismatch. Equation 4.2 gives the probability of a random match at a single locus, or the probability that a genotype has a matching allele by chance alone. If a genotype does not match by chance, then it is excluded from possibly being the parent. This means that the exclusion probability for a single individual sampled at random from a population is just 1 minus the probability of a random match:
$$
P(\mathrm{exclusion})=1-P(\mathrm{randommatch})
$$
如果从种群中采集了多个候选亲本,每个个体的排除概率是独立的(每个个体的基因型代表了种群中现存等位基因的随机采样)。因此,排除所有候选亲本的总概率是每个个体排除概率的乘积。对于从种群中采样的<math display="inline">n</math>个个体,总排除概率为
<math display="block">
P({\mathrm{exclusion~for}}n{\mathrm{individuals}})=(1-P({\mathrm{random~match}}))^{n}
</math>
这意味着随着从种群中采集更多个体,排除概率会降低。这等同于说:随着更多候选亲本被采样,仅通过随机性匹配到亲本单倍型的概率会增加。
基于<math display="inline">n</math>个候选亲本种群中的排除概率,我们可以估算随机匹配实际发生的概率。由于排除概率是非随机不匹配的概率,在<math display="inline">n</math>个个体的种群中候选亲本与子代单倍型匹配的概率即为1减去<math display="inline">n</math>个个体的排除概率,即
<math display="block">
\begin{array}{r l}&{P(\mathrm{randommatchin}n\mathrm{individuals})}\ &{=1-P(\mathrm{exclusionfor}n\mathrm{individuals})}\ &{=1-(1-P(\mathrm{randommatch}))^{n}}\end{array}
</math>
这是在<math display="inline">n</math>个候选亲本样本中随机出现与真实亲本匹配的单倍型的概率。
<math display="inline">n</math>个候选亲本样本中的随机匹配概率(式4.6)可理解为错误指派候选亲本为真实亲本的概率,因为其基因型通过随机性提供了匹配的单倍型,而真实亲本因未被包含在候选亲本样本中未被识别。这种现象在亲本分析中称为隐性基因流(cryptic gene flow),因为尽管错误推断了后代的亲本,真实的基因流动事件未被识别。若真实亲本因位于采样区域外而未被包含在候选亲本样本中,错误的亲本推断将导致基因流动距离的低估。式4.6表明:在给定预期基因型频率下,随着候选亲本数量的增加,因随机匹配导致错误亲本指派的概率会上升。
回到表4.2中的C. alta案例,我们可以确定以下概率:(1) 一个候选亲本被错误推断为父本,而真实父本未被检测到;(2) 在研究中30个候选亲本的父权排除概率。对于种子3-1,母本和父本相同(表4.4),表明这是一个自交事件。根据预期的父本单倍型频率,父权排除的概率为<math display="inline">(1 - (0.044)^{30} = 0.259)</math>,因此随机匹配的概率为0.741。由于这个四基因座推断的父本单倍型在30个候选亲本样本中预计会高频出现(74%的概率),即使种子实际由未包含在候选亲本样本中的个体授粉,它仍有可能被误判为自交。
对于种子989 1-1(候选亲本中仅包含1946号树),父权排除概率为<math display="inline">(1 - 0.0000665)^{30} = 0.9980</math>,因此随机匹配的概率为0.0020。根据等位基因频率估计,种子989 1-1的五基因座推断父本单倍型在30个候选亲本样本中预计仅以千分之二的概率随机出现。
问题框4.1 计算随机单倍型匹配概率和排除概率
来自母本树989的种子25-1与候选父本树4865显示完全单倍型匹配(见表4.2)。使用表4.3提供的等位基因频率,计算父本单倍型的随机匹配概率。然后,利用该随机匹配概率计算30个候选亲本样本的排除概率。哪些基因座对这两个种子后代的父权鉴定最有效和最低效?为什么?
交互框4.3 基因座的平均排除概率
亲本分析中每个子代-已知亲本对通常有以下四种结果:
- 确定单一候选亲本为父本:此类单一亲本归属需结合排除概率或亲本似然度进行解释。
- 单个子代对应多个候选亲本:此时常用标准是选择随机匹配概率最低的候选亲本作为父本。其他标准可能包括与已知亲本的空间隔离程度、生殖重叠度或生殖优势(若有相关数据)。
- 候选亲本中无个体能与已知亲本基因型组合产生子代基因型:表明真实亲本可能未包含在候选亲本样本中。此结果常被用于推断该子代来自样本区外的长距离基因流(即”非样地基因流”)。但也可能是真实亲本存在于候选亲本群体中,但在一个或多个基因座上存在遗传不匹配。
- 数据不足以明确归属或排除任何候选亲本:此时需通过增加基因座数或提高等位基因多态性来提升分辨率。
在规划亲权分析研究时,有必要确定一组遗传标记是否具有足够小的排除概率(这被称为遗传标记的效力)。如式4.4所示,排除概率将取决于单个亲本单倍型的期望基因型频率。这种期望基因型频率反过来又是每个位点的等位基因数量和等位基因频率的函数。由于具有三个或更多等位基因的位点存在许多可能的基因型,通常使用平均排除概率来评估一组遗传标记证明非父权的效力(参见Chakraborty et al. 1988;Weir 1996)。
您可以使用预先设置的Excel电子表格来计算一个具有6个等位基因的位点和一个具有12个等位基因的位点的平均排除概率(电子表格中缩写为<math display="inline">\mathsf{P_{E}}</math>)。该电子表格利用可修改的等位基因频率来计算:(i)每个母本-子代基因型组合的期望频率,以及(ii)每个母本-子代基因型组合对应的父本单倍型排除概率。平均排除概率是通过加权平均得到的,其中每个排除概率的权重是相应母本-子代基因型组合的期望频率。该电子表格遵循Chakraborty et al.(1988)表1中给出的三等位基因位点推导方法。当位点上所有等位基因具有相同频率时(例如6个等位基因时每个频率为1/6),平均排除概率达到最大值。每个电子表格中最大平均排除概率通过下式计算:
<math display="block">
{\mathsf{Max.prob.exclusion}}={\frac{(k-1){\Big(}k^{3}-k^{2}-2k+3{\Big)}}{k^{4}}}
</math>
其中<math display="inline">k</math>表示位点的等位基因数量(Selvin 1980)。
比较以下两种情况的平均排除概率:等位基因频率高度相似的情况,以及一个或少数等位基因频率极高而其余等位基因极为罕见的情况。等位基因频率的均匀性如何影响平均排除概率?如何将多个位点的平均排除概率进行组合?当每个位点的等位基因频率完全相等时,两个具有12个等位基因的位点或两个具有6个等位基因的位点的平均排除概率分别是多少?当存在50个候选亲本时,需要多少个具有12个等频率等位基因的独立位点才能达到90%的排除概率?
由于基因分型错误或突变。另一种可能是实际亲本在交配时位于候选亲本的采样区域内,但该个体在候选亲本采样前已死亡或迁出。
4 亲权被分配给某候选亲本,但真实亲本未被包含在可能亲本的样本中。在进行父权分配时,当父亲实际来自群体外部或发生”cryptic gene flow”事件时,在已采样的个体群体中错误分配父权的概率将与给定多位点基因型的期望频率相关。
亲本分析通过推断候选亲本群体中导致每个被采样后代或幼体的众多交配事件来测量基因流。这提供了诸如亲本间平均距离、双亲均位于采样区域内的交配次数与至少一个亲本位于该区域外的交配次数之比等参数的估计值。这意味着由此得出的基因流估计不依赖于任何种群结构或基因流模型,仅依赖于构建亲本分配时所用的假设前提。因此,这类基因流估计被视为”直接”测量方法。亲本分析的显著优势在于能够揭示交配模式细节,因为导致特定后代的亲本配对通常能以中等到高置信度被识别。
亲本分析已成为研究野生种群交配与亲缘关系模式的关键工具。典型案例是对鸟类巢雏的亲本分析研究,这些研究推翻了长期以来认为鸟类通常为一夫一妻制繁殖者的观点。实际上,鸟类具有多样且复杂的交配模式:雌雄个体在巢对之外的交配可能十分普遍,巢中的幼体可能与一只或两只”亲本”监护者均无亲缘关系(Westneat and Stewart 2003)。亲本分析还被广泛应用于各类动植物物种,用于详细描述交配与基因流模式。
尽管”直接”一词带有精确性和直观性的含义,但必须认识到亲本分析在推断基因流模式时确实存在局限性。主要限制源于大多数亲本研究最多仅覆盖几个世代的时间尺度。在所有种群数量稳定的生物中,平均每个亲本仅会产生一个能成功存活并繁殖的后代,其余后代或死亡或不育。这意味着亲本研究包含的许多(甚至可能是大多数)后代最终无法参与繁殖。这个问题在长寿生物中尤为突出——亲本研究仅考察了远短于个体平均寿命的时间段内产生的极少数后代。基因流可视为导致个体存活并为下一代贡献后代的交配事件的长期平均值。亲本分析估计长期基因流模式的有效性,取决于研究采样时长相对于世代时间的比例,以及短期亲本模式相对于其长期平均值的变异程度。
4.4 用固定指数总结种群分化模式
通过<math display="inline">F_{IS}</math>、<math display="inline">F_{ST}</math>和<math display="inline">F_{IT}</math>扩展固定指数来量化种群结构模式
本章的第一节回顾了导致种群间等位基因频率差异形成的各种过程。鉴于这些过程可能正在发生,有必要开发方法来测量和量化种群结构。当候选亲本样本和后代样本均具有基因型数据时,可进行如最后一节所述的亲权分析。另一种情况是对一系列地理区域内外的个体采样进行基因型数据测定。这种采样方式在实证研究中非常常见,需要开发方法来量化亚种群间存在的种群结构模式以及亚种群内的基因型频率分布。
若能将这些测量指标与无种群结构等参考情境的预期值进行直接比较,将具有重要优势。这类似于我们在第二章使用固定指数(<math display="inline">F</math>)比较观察杂合度与预期杂合度时采用的方法。现在我们可以将固定指数扩展到包含多个亚种群的情况。在这种更复杂的情形中,杂合体的哈迪-温伯格预期频率可能在两个层面出现偏差:由于非随机交配导致的亚种群内偏差,以及由于种群结构导致的亚种群间偏差。本节将推导并解释基于固定指数的指标,这些指标常用于通过偏离预期杂合度的程度来量化种群结构。
让我们详细考察一个案例:在多个亚种群中采集个体样本,测定双等位基因位点的基因型。回顾可知,种群中的杂合度等于1减去纯合度(<math display="inline">H=1-F</math>),因此杂合度可与固定指数相关联。利用此类基因型数据,可通过多种方式计算杂合体基因型的观察频率和预期频率(表4.5)。第一种方法是简单取平均值:
<math display="block">
H_{I}=\frac{1}{n}\sum_{i=1}^{n}\hat{H}_{i}
</math>
其中<math display="inline">\hat{H}</math>为每个<math display="inline">n</math>个亚种群中观察到的杂合体频率。我们可以将其记为<math display="inline">\overline{H}</math>,因为它是所有亚种群观察杂合体频率的平均值。这表示给定个体为杂合体的概率,或平均观察杂合度。如第二章所示,相对于哈迪-温伯格预期值,种群内杂合度可能因非随机交配而升高或降低。
表4.5 三个种群组织层次上杂合度的数学与生物学定义。求和式中,i表示各亚种群<math display="inline">1,2,3\dots n</math>,<math display="inline">p_{\mathrm{i}}</math>和<math display="inline">q_{\mathrm{i}}</math>为亚种群i中双等位基因位点上两个等位基因的频率。
| 符号
|
生物学定义
|
| <math display="inline">H_I=H</math>
|
各亚种群内观察杂合度的平均值
|
| <math display="inline">2p_iq_i</math>
|
各亚种群在随机交配假设下的预期杂合度(即<math display="inline">2pq</math>)
|
| <math display="inline">H_T=2pq</math>
|
使用总种群等位基因频率(<math display="inline">p</math>和<math display="inline">q</math>)计算的全种群预期杂合度(假设随机交配)
|
接下来,我们可以计算亚种群处于哈迪-温伯格平衡时的预期杂合度。这一假设意味着对于双等位基因位点,杂合基因型的预期频率为2pq。各亚种群的平均预期杂合度可表示为:
<math display="block">
H_{S}=\frac{1}{n}\sum_{i=1}^{n}2p_{i}q_{i}
</math>
其中<math display="inline">p_{i}</math>和<math display="inline">q_{i}</math>为第i个亚种群的等位基因频率,<math display="inline">n</math>为亚种群数量。我们也可以使用<math display="inline">\overline模板:2p q</math>符号表示,因为该值是通过先计算每个亚种群的预期杂合度再进行平均获得的。此处使用观测到的等位基因频率来估算各亚种群的哈迪-温伯格预期杂合度。
在分层种群结构的最顶层,我们可以计算总群体的预期杂合度:
<math display="block">
H_{T}=2\bar{p}\bar{q}
</math>
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/61ef9840d476acb0c9c23f69f56eff6fdc619ee862d8d61756534784b6509767.jpg
图4.10 分层群体中杂合度的层级结构示意图。<math display="inline">\begin{array}{r}{H_{1}=\frac{3}{10}}\end{array}</math>与<math display="inline">\begin{array}{r}{H_{2}=\frac{3}{10}}\end{array}</math>给出平均观测杂合度<math display="inline">\begin{array}{r}{H_{I}=\frac{1}{2}\left(\frac{3}{10}+\frac{3}{10}\right)=0.30}\end{array}</math>。若以<math display="inline">p</math>表示开放圆圈的等位基因频率,<math display="inline">q</math>表示实心圆圈的等位基因频率,则<math display="inline">p_{1}=13/20=0.65</math>,<math display="inline">q_{1}=1{-}p_{1}=0.35</math>;<math display="inline">p_{2}=7/20=0.35</math>,<math display="inline">q_{2}=1.p_{2}=0.65</math>。两个亚种群的平均预期杂合度为<math display="inline">H_{S}={}^{1}/2[2(0.65)(0.35)+2(0.35)(0.65)]=0.455</math>。总群体中等位基因平均频率为<math display="inline">\bar{p}=\%(0.65+0.35)=0.50</math>和<math display="inline">\overline模板:Q=\%{0.35+0.65})=0.50</math>,因此总群体的预期杂合度为<math display="inline">H_{T}=2\overline模板:P\overline模板:Q=2(0.5)(0.5)=0.5</math>。
式中<math display="inline">\bar{p}</math>和<math display="inline">\overline模板:Q</math>表示所有亚种群的等位基因平均频率。各亚种群的等位基因平均频率等同于将所有亚种群的等位基因合并为单一群体后估算的等位基因频率。换言之,这是在不考虑亚种群间分化的前提下,整个总群体的等位基因频率。因此,<math display="inline">H_{T}</math>表示当不存在群体遗传结构时,整个群体中杂合体的哈迪-温伯格预期频率。
这些观察到的和预期的杂合度水平在图4.10中以总种群由两个亚种群组成的情况为例进行了图示,每个亚种群包含10个二倍体个体。在两个亚种群中,10个个体中有3个是杂合体,给出观察到的杂合体频率为<math display="inline">\begin{array}{r}{H_{1}=\frac{3}{10}\mathbf{and}H_{2}=\frac{3}{10}.}\end{array}</math> 综合来看,这产生了平均观察杂合度为<math display="inline">\begin{array}{r}{H_{I}=\frac{1}{2}\left(\frac{3}{10}+\frac{3}{10}\right)=0.30}\end{array}</math>。
要确定亚种群的平均预期杂合度需要每个亚种群的观察等位基因频率。在第一个亚种群中,20个等位基因中有13个是红色,7个是蓝色。若<math display="inline">p</math>为红色等位基因频率,<math display="inline">q</math>为蓝色等位基因频率,则<math display="inline">p_{1}=13/20=0.65</math>且<math display="inline">q_{1}=1-p_{1}=0.35</math>。在第二个亚种群中,情况完全相反,<math display="inline">p_{2}=7/20=0.35</math>且<math display="inline">q_{2}=1-p_{2}=0.65</math>。两个亚种群的平均预期杂合度则为<math display="inline">H_{S}={\textstyle\frac{1}{2}}[2(0.65)(0.35)+2(0.35)(0.65)]=0.455</math>。
在总种群中,平均等位基因频率为<math display="inline">\textstyle{\overline模板:P}={\frac{1}{2}}(0.65+0.35)=0.50</math>和<math display="inline">\overline模板:Q=\textstyle{\frac{1}{2}}(0.35+0.65)=0.50</math>。(注意:对亚种群等位基因频率取平均等价于合并总种群中所有等位基因后估计等位基因频率,如<math display="inline">\textstyle{\overline模板:P}={\frac{13+7}{40}}=0.50</math>。)总种群的预期杂合度则为<math display="inline">H_{T}=2(0.5)(0.5)=0.5</math>。
通过计算图4.6中不同观察和预期杂合度后,显然它们并不完全等同。在种群不同层级水平上观察和预期杂合度之间存在差异。回顾第2.5节可知,观察值与Hardy–Weinberg预期基因型频率的差异被用于估计固定指数或<math display="inline">F</math>。在这种情况下,仅涉及单一种群,且我们只关注等位基因如何组合成二倍体基因型与随机交配预期的比较。固定指数可扩展以适应种群组织的多个层级,从而创建衡量由两种不同过程引起的偏离Hardy–Weinberg预期基因型频率的指标。对于多个亚种群,可能存在因亚种群内非随机交配导致的杂合体过量或不足,以及与泛交相比亚种群间杂合体可能的不足。在后一种情况下,固定指数将显示由于导致种群结构的过程,亚种群间等位基因频率相比泛交所预期的亚种群间等位基因频率均匀的理想状态发生了多大程度的分化。
表4.6 两个层次种群组织中固定指数的数学和生物学定义。
<table><tr><td>Hs-Hi Fis=— Hs</td><td>各亚种群内由于非随机交配导致的平均观测杂合度与平均Hardy-Weinberg预期杂合度之差。任意亚种群随机抽样基因型中两个等位基因状态的相关性。由等位基因频率亚种群分化导致的杂合度降低。亚种群平均预期杂合度与</td></tr></table>
考虑非随机交配和亚种群等位基因频率分化需要多个新版本的固定指数。表4.6展示了这些新固定指数的定义。让我们以图4.6为例应用并解释这些固定指数的各个版本。$F_{I S}$比较每个亚种群内个体的平均观测杂合度与所有亚种群的Hardy-Weinberg平均预期杂合度(I代表个体,$S$代表亚种群)。$F_{I S}$与2.5节中使用的单种群$F$相同,只是现在它是所有亚种群的平均值。使用上述确定的杂合度:
$$
F_{I S}={\frac{0.455-0.30}{0.455}}=0.341
$$
# 问题框4.2 计算$F_{I S},F_{S T}$和${\cal F}_{I T}$
这个结果具有生物学意义——在给定亚种群等位基因频率的情况下,每个亚种群中的杂合子数量比随机交配预期的更少。因此,两个亚种群中的纯合性或固定程度比随机交配预期更高。若存在近亲交配,亚种群平均杂合度缺失符合预期。
层级结构的下一层次是亚种群平均预期杂合度与总种群预期杂合度的比较,即$F_{S T}$($S$代表亚种群,$T$代表总种群)。根据先前确定的杂合度:
$$
F_{S T}=\frac{0.50-0.455}{0.50}=0.09
$$
该结果表明,与理想情况下(整个种群为panmictic时)的预期杂合度相比,两个亚种群的平均杂合度略低。这与两个亚种群具有轻微不同的等位基因频率、每个亚种群的预期杂合度略低于1/2的事实一致。然而,若两个亚种群间没有等位基因频率分化,总种群的杂合度应为1/2(最大值)。
层级结构的最终层次是$F_{I T}$,即亚种群平均观测杂合度与总种群预期杂合度的比较:
$$
F_{I T}=\frac{0.50-0.30}{0.50}=0.40
$$
这给出了由于亚种群内非随机交配和亚种群间等位基因频率分化的共同作用,导致的Hardy-Weinberg预期基因型频率的综合偏离。在此例中,纯合性增加40%或杂合性减少60%,相较于具有相同等位基因频率的理想随机交配panmictic种群的预期值。
Levin (1978) 使用等位酶电泳技术估测了Phlox cuspidata(一种能够自花授粉的植物)中磷酸葡萄糖变位酶-2基因(Pgm-2)的基因型频率。遗传数据采集自该物种在德克萨斯州东南部分布区内的43个种群。通过淀粉凝胶电泳技术,记录了每个种群中两个等位基因(快速迁移型和慢速迁移型)的频率以及杂合基因型的频率。部分数据如下表所示(种群编号与Levin (1978) 的表2对应)。
|
|
Subpopulation
|
|
|
1 9
|
| —————————-
|
——————
|
| Frequency of Pgm-2 fast
|
0.0 0.93
|
| Frequency of Pgm-2 slow
|
1.0 0.07
|
| Heterozygote frequency
|
0.0 0.14
|
利用杂合子频率和等位基因频率,计算分层杂合度<math display="inline">H_{I}</math>、<math display="inline">H_{S}</math>和<math display="inline">H_{T}</math>,并用这些值计算<math display="inline">F_{I S}</math>、<math display="inline">F_{S T}</math>和<math display="inline">\bar{F}_{I T}</math>。是否有证据表明P. cuspidata个体存在自交行为?这些种群是随机交配的还是存在亚群分化?
在补偿观察杂合度与预期杂合度在不同种群组织层次上的偏差后,个体、亚群和总种群层次的杂合度将趋于一致。亚群的平均观察杂合度会高于或低于其平均预期杂合度:
<math display="block">
H_{I}=H_{S}(1-F_{I S})
</math>
这反映了非随机交配的程度(<math display="inline">F_{I S}\neq</math> 0)。类似地,亚群的平均预期杂合度会低于随机交配条件下总种群的预期杂合度:
<math display="block">
H_{S}=H_{T}\big(1-F_{S T}\big)
</math>
这反映了亚群间等位基因频率的分化程度(<math display="inline">F_{S T}>0</math>)。亚群内和亚群间相对于预期杂合度的总偏离可表示为:
<math display="block">
H_{I}=H_{T}\big(1-F_{I T}\big)
</math>
尽管公式4.14–4.16可视为公式4.11–4.13的重排形式,但它们还体现了另一种理解亚群间等位基因频率分化和亚群内非随机交配对生物学影响的方式。每个固定指数均反映了杂合基因型频率与随机交配预期的偏离程度。同时可以证明,杂合度的总减少量与非随机交配和亚群分化共同导致的固定效应相关:
<math display="block">
1-F_{I T}=\big(1-F_{S T}\big)\big(1-F_{I S}\big)
</math>
由于使用固定指数来衡量亚群体间等位基因频率的分化是本节的新概念,让我们再考虑一个专门聚焦于<math display="inline">F_{ST}</math>的案例。图4.11展示了一个双等位基因位点在两个由六个亚群体组成的群体中的等位基因频率分布。两组亚群体间的等位基因频率模式存在显著差异:右侧所有亚群体具有相同的等位基因频率,而左侧每个亚群体均处于一个等位的完全固定或完全丢失状态。
在这两种群体结构中,总群体的期望杂合度<math display="inline">H_T=2(0.5)(0.5)=0.5</math>。两者唯一差异在于等位基因频率的组织方式,即亚群体内期望杂合度<math display="inline">H_S</math>。右侧群体中,六个亚群体的等位基因频率均为1/2,因此<math display="inline">H_S=(6(2)(0.5)(0.5))/6=0.5</math>;左侧群体中,三个亚群体等位基因频率为零,另三个为1,计算得<math display="inline">H_S=(3(2)(1.0)(0)+3(2)(0)(1.0))/6=0.0</math>。通过这些亚群体与总群体的期望杂合度计算可得:右侧<math display="inline">F_{ST}=0.0</math>,左侧<math display="inline">F_{ST}=1.0</math>。
虽然两种情况下总群体的平均等位基因频率相同,但等位基因频率的组织方式存在本质差异。右侧各亚群体具有完全一致的等位基因频率,如同未发生群体分化;左侧则呈现强烈亚群体分化的预期模式。因此,不同的<math display="inline">F_{ST}</math>值反映了不同水平的等位基因频率分化程度。
当所有亚群体充分混合且具有相似等位基因频率时,<math display="inline">H_S</math>与<math display="inline">H_T</math>相等。生物学上,<math display="inline">F_{ST}=0</math>意味着所有亚群体的等位基因频率与总群体一致,各亚群体间杂合体数量无差异。随着群体因各种过程导致等位基因频率分化,<math display="inline">H_S</math>将降低而<math display="inline">F_{ST}</math>趋近于1。生物学上,<math display="inline">F_{ST}=1</math>表明遗传变异完全体现为亚群体间的等位基因频率差异,而亚群体内部不存在等位基因的分离状态。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/59d36ac5ccf3ca640d341f01ff5957384296bfe5fd8c196e08d96dfdb0d40e40.jpg
图4.11 由六个亚群体组成的群体在一个双等位基因位点上的等位基因频率。亚群体内的等位基因频率通过着色表示。左侧,单个亚群体对某一等位基因呈现固定或丢失状态。右侧,所有亚群体具有相同的等位基因频率<math display="inline">p=q=0.5</math>。在两种情况下,整个群体的平均等位基因频率为<math display="inline">\overline{p}=0.5</math>,期望杂合度为<math display="inline">H_{T}=2\overline{p}\overline{q}=0.5</math>。与之相对,亚群体的平均期望杂合度在右侧为<math display="inline">H_{S}=\overline{2pq}=0.5</math>,在左侧为<math display="inline">H_{S}=\overline{2pq}=0.0</math>。右侧<math display="inline">F_{ST}=1.0</math>,因为亚群体间具有最大分化的等位基因频率。左侧<math display="inline">F_{ST}=0.0</math>,因为所有亚群体具有相同的等位基因频率。亚群体间等位基因频率的分化会导致杂合度相对于基于整个群体平均等位基因频率的Hardy–Weinberg预期出现缺失。
另一种理解等位基因频率群体分化模式的方法是通过等位基因频率的方差相对于整个群体遗传变异的量来估计<math display="inline">F_{ST}</math>。亚群体间等位基因频率分化的估计值为:
<math display="block">
F_{ST}=\frac{\mathrm{var}(p)}{\bar{p}\overline{q}}
</math>
其中<math display="inline">n</math>个亚群体间的等位基因频率方差为<math display="inline">\operatorname{var}(p)={\frac{1}{n}}\sum_{i=1}^{n}\left(p_{i}-{\overline{p}}\right)^{2}</math>,且假设存在极大量亚群体(Wright 1943a)。若等位基因频率的方差越大,则亚群体间等位基因频率差异越大,由此产生的<math display="inline">F_{ST}</math>也越大。例如,在图4.7中,两组六个亚群体的平均等位基因频率<math display="inline">\bar{p}</math>均为0.5。右侧,<math display="inline">p</math>的方差为<math display="inline">\frac{3{\left(\left(0-0.5\right)^{2}\right)}+3{\left(\left(1-0.5\right)^{2}\right]}}{6}=0.25</math>;而左侧,<math display="inline">p</math>的方差为<math display="inline">6(0.5−0.5)^{2}=0.0</math>。这导致右侧(亚群体间存在最大等位基因频率方差时)<math display="inline">F_{ST}=1.0</math>,而左侧(亚群体间无等位基因频率方差时)<math display="inline">F_{ST}=0.0</math>。基于实际遗传标记数据估计<math display="inline">\hat{F}_{ST}</math>的几种广泛应用方法,其核心正是测量亚群体间等位基因频率的方差。
估计固定指数
本节始终使用双等位基因的单个位点来说明分层杂合度与固定指数。这些示例较为简单,可视为参数概念的推导。实际操作中,获取固定指数参数估计值<math display="inline">\hat{F}_{IS}</math>、<math display="inline">\hat{F}_{ST}</math>和<math display="inline">\hat{F}_{IT}</math>涉及大量细节。每个固定指数的估计方法都基于一系列假设,这些假设反映了所用遗传数据类型(如DNA序列多态性或微卫星可变位点)以及对基因流、遗传漂变和突变速率的假设。选择估计方法并正确解释其结果,需要理解这些假设及其与生物过程模型的联系(见Rousset 2013)。
<math display="inline">G_{ST}</math> 是一种广泛使用的亚种群相对于总种群固定程度的估计量,当位点具有两个以上等位基因时,它平均了杂合度(Nei 称为基因多样性),并平均了多个位点的杂合度(Nei 1973)。Weir 和 Cockerham(1984)提出了等位基因的共祖系数以及种群间固定程度的估计量 <math display="inline">\uptheta_{ST}</math>(读作“theta”),该估计量对实际数据的特征(如位点和亚种群间可变的样本量以及位点间不同数量的等位基因)进行了严格的统计处理(另见 Weir 1996;Weir 和 Goudet 2017)。Excoffier 等人(1992)开发了类似于亚种群内和亚种群间等位基因状态差异方差分析的估计量。这种方法称为分子方差分析或 AMOVA,基于对等位基因状态差异的测度(记为 <math display="inline">d</math>)从种群层级的不同水平中抽样估计 <math display="inline">\Phi</math>(读作“phi”)。亚种群间遗传分化的 AMOVA 估计量为: <math display="block">
\Phi_{ST}=\frac{d_{T}-d_{S}}{d_{T}}
</math> 其中 <math display="inline">d_{T}</math> 是总种群中所有等位基因对间等位基因状态差异的平均值,<math display="inline">d_{S}</math> 是各亚种群内所有等位基因对间等位基因状态差异平均值在所有亚种群中的平均。(等位基因状态差异对遗传距离测度的具体贡献方式取决于突变模型,如第 5 章所述。)最后,估计量 <math display="inline">\uprho_{ST}</math>(读作“roe”)或 <math display="inline">R_{ST}</math> 常用于微卫星或简单序列重复位点,以解释可能掩盖种群结构的高频逐步突变(Slatkin 1995;见第 5 章)。这些估计量的解释方式均与双等位基因版本的固定指数相同。
Wright 最初推导固定指数时假设位点最多有两个等位基因,且突变率极低,因此对等位基因频率或新等位基因的引入影响极小。相对近期,微卫星遗传位点被广泛应用于种群分化研究。由于高突变率,微卫星位点通常在每个位点上表现出多个等位基因。虽然具有两个等位基因的位点最大期望杂合度为 0.5,但具有多个等位基因的位点由于每个等位基因的频率可能仅为几个百分点,其最大期望杂合度可接近 1。每个位点上如此高的等位基因多样性导致总种群的期望杂合度 <math display="inline">H_{T}</math> 也较高,并使 <math display="inline">\Delta G_{ST}</math> 的最大值小于 1。图 4.12 展示了在有限岛屿模型模拟中当 <math display="inline">H_{T}</math> 极高时 <math display="inline">G_{ST}</math> 的示例。这反映了更普遍的现象:<math display="inline">F_{ST}</math> 的范围是等位基因频率的函数(见 Jakobsson 等人 2013;Alcala 和 Rosenberg 2017 及其参考文献)。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/54a3af3f76da96fa42899bec4c1b795b1b0805d404c32fa3239f392e02b4c259.jpg
图4.12 有限岛屿模型模拟中的遗传分化,展示了当位点具有两个以上等位基因时<math display="inline">G_{ST}</math>、<math display="inline">G_{ST}^{\prime}</math>和<math display="inline">D</math>作为估计量的差异。面板A的位点具有三个等位基因,面板B的位点具有十个等位基因。该模拟在包含20个亚群体(每个亚群体含10个个体)的有限岛屿模型中运行200代,使用10个重复的中性位点,基因流速率<math display="inline">m=0.0005</math>。<math display="inline">G_{ST}</math>、<math display="inline">G_{ST}^{\prime}</math>和<math display="inline">D</math>为使用所有位点的多位点估计值。
针对<math display="inline">G_{ST}</math>不可能超过亚群体内平均纯合度的观察,Hedrick(2005)提出了一个通过最大可能值重新标定的<math display="inline">G_{ST}</math>版本:
<math display="block">
G_{S T}^{\prime}={\frac{G_{S T}}{{\frac{1-H_{s}}{1+H_{s}}}}}
</math>
(假设亚群体数量较大)。这使得遗传分化的测量值始终介于0到1之间,类似于标准化配子不平衡系数(见第2章)。Hedrick认为,只要突变速率远小于基因流速,<math display="inline">G_{ST}^{\prime}</math>能够在多样性水平差异显著时更准确地进行遗传分化比较。
同样受到高杂合度案例的启发,Jost(2008,2009)提出了一个估计量,用于测量亚群体完全分化的偏离程度:
<math display="block">
\begin{array}{r}{D=\left(\frac{d}{d-1}\right)\frac{H_{T}-H_{S}}{1-H_{S}}}\end{array}
</math>
其中<math display="inline">d</math>为有限岛屿模型中的亚群体数量。
Jost的论文引发了争议,并重新激起了关于遗传分化估计量的讨论。对Jost论文的回应帮助澄清了<math display="inline">D</math>及固定指数中的隐含假设(Heller和Siegismund 2009;Ryman和Leimar 2009;Whitlock 2011;Verity和Nichols 2014;Jost等2018)。虽然<math display="inline">F_{ST}</math>测量亚群体间偏离随机交配的程度,但Jost的<math display="inline">D</math>测量亚群体间偏离完全分化的程度。
基于对有限岛屿模型中基因流和突变对多种遗传分化测量指标影响的研究,Whitlock(2011)指出<math display="inline">G_{ST}^{\prime}</math>和<math display="inline">D</math>不是有效的群体遗传分化指标,主要原因有二。首先,目前难以将<math display="inline">G_{ST}^{\prime}</math>和<math display="inline">D</math>的估计值与遗传漂变和基因流等关键进化速率参数相连接(见第4.6节)。其次,<math display="inline">G_{ST}</math>、<math display="inline">G_{ST}^{\prime}</math>和<math display="inline">D</math>的数值均依赖突变速率。当突变速率相对于基因流速较高时,<math display="inline">G_{ST}</math>的遗传分化值会因突变降低血统同一性而减小(更多讨论见第5章)。相反,<math display="inline">G_{ST}^{\prime}</math>和<math display="inline">D</math>往往保持接近1,尤其在亚群体数量较多时,无法区分导致高值的具体过程。见图4.12比较不同等位基因数量和总群体杂合度水平下<math display="inline">G_{ST}</math>、<math display="inline">G_{ST}^{\prime}</math>和<math display="inline">D</math>的表现。
在 Whitlock 的研究中,当突变率较高且亚种群数量较大时,<math display="inline">G_{S T}^{\prime}</math>并未随基因流速率的不同而发生显著变化。对于<math display="inline">D</math>而言,当基因流速率相对较高时,其值对突变率也较为敏感,导致位点间突变率的变异也会使<math display="inline">D</math>表现出较高的位点间变异。相比之下,当突变率远低于基因流速率时,<math display="inline">G_{S T}</math>不受影响。例如,若突变率相似,比较两个物种的遗传分化可通过<math display="inline">G_{S T}^{\prime}</math>辅助,但突变率通常未知,难以支持此类比较。Whitlock 的论文强调了固定指数如何与遗传漂变、基因流和突变速率的预测密切相关,并指出选择群体遗传分化的估计量应基于对底层模型的了解以及假设检验的目标。
4.5 种群细分与 Wahlund 效应
遗传变异可表现为随机交配种群内的杂合性,或分化亚群间的等位基因频率差异。
本章前一节展示了如何利用杂合子 Hardy-Weinberg 预期频率的偏离来量化群内随机交配的偏离以及群间等位基因频率的分化。本节将进一步探讨多个群内与群间的杂合性,主要有两个目标:第一是探究种群细分对预期基因型频率的影响,第二是说明为何<math display="inline">F_{S T}</math>可用于估计群间等位基因频率的分化。
考虑两个随机交配群的双等位基因位点案例。每个群的预期杂合度为:
<math display="block">
H_{i}=2p_{i}q_{i}
</math>
其中<math display="inline">i</math>表示单个亚种群。两个群的平均杂合度基于各亚种群内杂合度的平均:
<math display="block">
H_{S}=\frac{2p_{1}q_{1}+2p_{2}q_{2}}{2}
</math>
相比之下,总种群的杂合度为:
<math display="block">
{\cal H}_{T}=2\overline{{{p}}}\overline{{{q}}}
</math>
基于亚种群平均等位基因频率的乘积。<math display="inline">H_{T}</math>和<math display="inline">H_{S}</math>均不可超过 0.5(双等位基因位点的最大杂合度)。此外,<math display="inline">H_{S}</math>是<math display="inline">H_{1}</math>和<math display="inline">H_{2}</math>的平均值,因此当细分种群的等位基因频率不同时,<math display="inline">H_{S}</math>始终小于总种群的预期杂合度。这些条件确保了当亚种群内为随机交配时,<math display="inline">H_{T}\geq H_{S}</math>。<math display="inline">H_{T}</math>与<math display="inline">H_{S}</math>的关系如图 4.13 所示。此现象称为 Wahlund 效应,得名于 1928 年首次描述该现象的瑞典遗传学家 Sten Gosta William Wahlund。其结果是,由于<math display="inline">F_{S T}</math>表达式中的分子为<math display="inline">H_{T}-H_{S}</math>,<math display="inline">F_{S T}</math>将大于或等于 0。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/b4186b540326e9c5d467a54e1eece5ae6b38756b96a3628369a57a5bb2112dc2.jpg
图 4.13 两个同类群中双等位基因位点的Wahlund效应图示。若亚群内(<math display="inline">H_{1}</math>和<math display="inline">H_{2}</math>)和总群体(<math display="inline">H_{T}</math>)均为随机交配,则各群体的杂合度均落在Hardy-Weinberg期望频率的抛物线上。亚群的平均杂合度(<math display="inline">H_{S}</math>)位于同类群杂合度之间的中点。因此,基于平均等位基因频率(同类群等位基因频率<math display="inline">p_{1}</math>和<math display="inline">p_{2}</math>的中点),<math display="inline">H_{S}</math>永远不可能超过<math display="inline">H_{T}</math>。同类群等位基因频率的更大方差等价于两同类群情形下更宽的等位基因频率分布。
Wahlund效应:相较于具有相同总规模和相同平均等位基因频率的随机交配群体,等位基因频率分化的亚群中杂合子的期望频率降低。
Wahlund效应还可通过另一种方式展示,更清晰地将其与亚群间等位基因频率的变异联系起来。接下来将证明总群体预期杂合度(<math display="inline">H_{T}</math>)与亚群平均预期杂合度(<math display="inline">H_{S}</math>)的差异取决于亚群间等位基因频率的方差。
一组亚群间等位基因频率的方差为:
<math display="block">
\operatorname{Var}(p)={\frac{\sum\left(p_{i}-{\overline模板:P}\right)^{2}}{n}}={\frac{\sum{p_{i}}^{2}}{n}}-{\overline模板:P}^{2}
</math>
其中<math display="inline">p_{i}</math>为亚群<math display="inline">i</math>的等位基因频率。对于双等位基因位点,<math display="inline">\mathrm{var}(p)</math>等于<math display="inline">{\mathrm{var}}(q)</math>,因为<math display="inline">p=1-q</math>。此结果将在后续使用。
亚群的平均预期杂合度:
<math display="block">
H_{S}=\frac{1}{n}\sum_{i=1}^{n}2p_{i}q_{i}
</math>
也可表示为:
<math display="block">
H_{S}=\sum_{n}2\left(\frac{p_{i}}{n}-\frac{{p_{i}}^{2}}{n}\right)
</math>
注意到<math display="inline">p_{i}q_{i}=p_{i}(1-p_{i})=p_{i}-{p_{i}}^{2}</math>(因<math display="inline">p=1-q</math>),可将该式重排为:
<math display="block">
H_{S}=2\left(\frac{\Sigma p_{i}}{n}-\frac{\Sigma p_{i}{}^{2}}{n}\right)
</math>
括号内的右侧项与等位基因频率方差表达式中的一项相同。将式4.22重排得<math display="inline">{\frac{\sum p_{i}^{~2}}{n}}=\operatorname{var}(p)+{\overline模板:P}^{2}</math>,代入后得到:
<math display="block">
H_{S}=2\left({\frac{\Sigma p_{i}}{n}}-\operatorname{var}(p)-{\overline模板:P}^{2}\right)
</math>
通过观察可知<math display="inline">{\frac{\Sigma p_{i}}{n}}</math>即为平均等位基因频率<math display="inline">\overline模板:P</math>,代入后简化为:
<math display="block">
H_{S}=2\left(\overline{{{p}}}-\overline{{{p}}}^{2}-\mathrm{var}(p)\right)
</math>
接下来利用<math display="inline">p=1-q</math>将<math display="inline">\overline模板:P-\overline模板:P^{2}</math>替换为等效表达式<math display="inline">\bar{p}\bar{q}</math>,并将括号内各项乘以2,最终得到:
<math display="block">
H_{S}=2\overline模板:P\overline模板:Q-2\mathrm{var}(p)
</math>
由式4.21可知<math display="inline">H_{T}=2\overline模板:P\overline模板:Q</math>,代入后可得:
当<math display="inline">\mathrm{var}(p)>0</math>时,纯合子相较于泛交情形存在过量。此方法还预测:杂合子的总缺失量将等于纯合子的总过量量。
瓦尔亨德效应(Wahlund effect)是更普遍现象的一个例子,这种现象发生在对非线性函数的多个值进行平均时,并且是詹森不等式原理(Jensen’s inequality)的基础,该原理在生态学和演化生物学中有众多应用(见Ruel和Ayres 1999)。
<math display="block">
H_{S}=H_{T}-2\mathrm{var}(p)
</math>
交互框4.4 模拟瓦尔亨德效应
通过一系列等效的代换和代数重排,还可以证明亚群中纯合基因型的预期频率为
<math display="block">
F r e q(A A)_{S}=\overline模板:P^{2}+\mathrm{var}(p)
</math>
<math display="block">
F r e q(a a)_{S}=\bar{q}^{2}+\mathrm{var}(p)
</math>
以及
由种群间等位基因频率分化引起的纯合性与杂合性变化,与单一种群中近亲交配(consanguineous mating)的后果完全类似。在第2.6节中已证明 <math display="inline">f r e q(A A)=p^{2}+f p q</math>,其中 <math display="inline">f</math> 是血源同一性(identity by descent)的概率。瓦尔亨德效应描述了类似现象:种群的等位基因频率分化导致亚群中的纯合性增加,超出基于总种群等位基因频率预期的杂合性水平。
这些方程表明,在分化的种群中,亚群的预期基因型频率是总种群平均等位基因频率以及亚群间等位基因频率方差的函数。一组处于随机交配(panmixia)的亚群等价于等位基因频率方差为零 <math display="inline">(\mathrm{var}(p)=0)</math> 的情况。此时,<math display="inline">H_{T}=H_{S}</math>,且 <math display="inline">F_{S T}</math> 为0,因为 <math display="inline">H_{T}-H_{S}</math> 也为0。这一结果符合直观预期:广泛的基因流会使亚群间的等位基因频率均质化。然而,当亚群的等位基因频率发生分化且方差 <math display="inline">\mathrm{var}(p)>0</math> 时,总种群将出现杂合子缺失,且
瓦尔亨德效应作为非线性平均化的结果,可以通过在德菲内蒂图(de Finetti plot,或三元图)上绘制两个亚群的基因型频率直观呈现。教材网页链接的网站提供了相关解释和可用的R代码片段。
尝试使用默认基因型频率值(其中 <math display="inline">f=0</math>)进行第一次模拟。调整两个亚群的等位基因频率使其分化程度增大或减小。当你在亚群内尝试不同水平的非随机交配(即 <math display="inline">\boldsymbol{\hat{{\mathbf{\mathit{\Pi}}}}}</math> 取非零值)时,观察到的基因型频率会发生什么变化?
Wahlund 效应的一个后果被称为 isolate breaking(隔离打破),用于描述当先前因等位基因频率分化而分化的亚种群经历随机交配时,杂合子基因型频率的增加。在人类种群中,由纯合子中表达的隐性等位基因引起的疾病表型包括 cystic fibrosis、albinism、Tay–Sachs disease 和 sickle cell anemia。这些疾病在相对孤立的种群(如 Ashkenazi Jews、native American groups 和 Amish)中更为常见,但在经历更多基因混合的人类种群中较为罕见——这些种群因亚分化导致的杂合子缺失较少。
为理解 isolate breaking 的影响,假设两个随机交配的松鼠种群最初不存在任何迁移,且等位基因频率随时间分化(图4.14)。假设左侧种群中存在白化个体,其表型由完全隐性等位基因 a 决定,频率为 <math display="inline">q</math>,而右侧种群中完全缺乏该白化等位基因。亚分化种群中白化松鼠的平均频率为:
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/b5a39d8aae9abf8df7535fb574fbcad3857786931a92f58bd3bf8049d412964f.jpg
图4.14 Wahlund 效应如何关联亚种群间等位基因频率变异与单一随机交配种群中基因型频率的假想示例。最初,两个亚种群具有不同的等位基因频率,因此隐性纯合白化表型的频率也不同。白化表型的平均频率在亚种群中为 <math display="inline">8\%</math>。当种群融合后,等位基因频率变为两个亚种群的平均值。然而,基因型频率并非两个亚种群的平均值。相反,纯合子频率低于亚种群平均值,而杂合子频率高于亚种群平均值。在融合种群中,两种纯合子组合频率与杂合子频率偏离其亚种群平均值的程度,等于两个亚种群间等位基因频率的方差。
基于 Hardy–Weinberg 定律,我们同样可以计算两个亚种群中显性纯合子的平均频率(<math display="inline">p² = \overline{{p^{2}}}=\frac{0.36+1.0}{2}=0.68</math>)和杂合子的平均频率(<math display="inline">\overline模板:2p q=\frac{0.48+0.0}{2}=0.24</math>)。
接着,假设两个松鼠种群融合为一个随机交配的种群。在随机交配发生后,融合种群中隐性等位基因的频率及白化松鼠的预期频率是多少?首先确定融合种群的等位基因频率:
<math display="block">
q_{f u s e d}=\frac{0.4+0.0}{2}=0.2
</math>
然后用该结果计算融合种群中隐性纯合基因型的预期频率:
<math display="block">
q^{2}{}_{f u s e d}=\left({\frac{0.4+0.0}{2}}\right)^{2}=\left(0.2\right)^{2}=0.04
</math>
在融合种群中,白化松鼠的比例(4%)低于两个细分种群的平均值(8%)。可以验证其他纯合子在融合种群中的频率也有所下降。与细分种群的平均频率相比,两种纯合子的频率在融合种群中均下降了4%。相比之下,融合种群中杂合子的频率
<math display="block">
2pq_{fused}=2(0.2)(0.8)=0.32
</math>
高于细分种群杂合子的平均频率(见表4.7)。
现在让我们计算融合前后两个种群间等位基因频率的参数方差。初始时,两个细分种群的等位基因频率方差为
<math display="block">
\operatorname{Var}(q)={\frac{\left(0.4-0.2\right)^{2}+\left(0.0-0.2\right)^{2}}{2}}=0.08
</math>
而融合后方差<math display="inline">(q)</math>为0,因为不再存在等位基因频率的细分。需注意初始等位基因频率方差(0.08)正好是融合前白化体平均频率与融合后预期白化体频率差值的一半。随着细分种群的融合,每个纯合子频率减少了4%,而杂合子频率则增加了完全相同的总量(即8%)。
表4.7 图4.9中假想白化松鼠案例的等位基因和基因型频率,用于展示Wahlund原理。初始时总种群被细分为两个具有不同等位基因频率的繁殖群,随后这两个种群融合并经历一代随机交配。
|
|
Initial subpopulations
|
Fused population
|
| Allele frequency q
|
0.4 and 0.0
|
<math display="inline">\frac{0.4+0.0}{2}=0.2</math>
|
| Variance in q
|
<math display="inline">\frac{(0.4-0.2)^2 + (0.0-0.2)^2}{2}=0.04</math>
|
0
|
| Frequency of aa
|
<math display="inline">\frac{0.16+0.0}{2}=0.08</math>
|
<math display="inline">(0.2)^2=0.04</math>
|
| Frequency of Aa
|
<math display="inline">\frac{0.48+0.0}{2}=0.24</math>
|
<math display="inline">2(0.2)(0.8)=0.32</math>
|
| Frequency of AA
|
<math display="inline">\frac{0.36+1.0}{2}=0.68</math>
|
<math display="inline">(0.8)^2=0.64</math>
|
这个例子表明,通过将两个亚群体融合为一个随机交配群体来消除它们之间的等位基因频率差异,改变了总群体的杂合性。结果正是Wahlund效应所预测的:在随机交配下总群体的杂合性高于亚群体分化状态。分化的种群以总群体杂合性为代价,将部分遗传变异存储为种群间等位基因频率差异(变异)。另一种理解方式是:种群分化相当于近亲交配,这会增加总群体的纯合性(或减少总群体的杂合性)。融合的或随机交配的群体比基因流动受限的孤立分化亚群体具有更大的有效种群大小。在亚群体中,交配更可能发生在亚群体内部而非与总群体的迁移个体之间。因此,与同等规模的随机交配群体相比,亚群体具有更高的自合性,类似于单一有限种群因遗传漂变导致的杂合性下降现象。
Wahlund原理的一个应用实例可见于法医DNA分型。如第2.4节所述,使用DNA标记确定特定基因型随机出现的预期频率时,需要参考不同种族定义的人类群体中等位基因频率的估计值。尽管DNA分型所用位点的等位基因频率已在许多群体中进行过估计,但可供使用的参考等位基因频率数据库数量有限。因此,某些个体可能因其种族、民族或地理背景而缺乏对应的群体特异性等位基因频率估计数据。更复杂的是,许多个体具有多元种族血统,这可能无法被任何单一组现有参考等位基因频率所代表。如果人类群体呈现随机交配状态,DNA分型就不会存在这些问题,因为所有种族定义的人类群体都将具有统一的等位基因频率。然而,用于构建等位基因频率参考数据库的种族和地理定义人类群体显示,其等位基因频率存在高达<math display="inline">3{-}5\%</math>的群体间差异(Rosenberg et al. 2002)。
我们可以运用Wahlund原理调整DNA分型概率比,以校正种群结构的影响。这需要一种方法来调整每个位点的预期基因型频率,从而反映由群体间等位基因频率差异导致的纯合子频率增加和杂合子频率降低。纯合子基因型的校正预期频率为:
<math display="block">
f(A_{i}A_{i})=p_{i}^{2}+p_{i}(1-p_{i})F_{I T}
</math>
杂合子基因型的校正预期频率为:
<math display="block">
f\big(A_{i}A_{j}\big)=2p_{i}p_{j}-\big(2p_{i}p_{j}\big)F_{I T}=2p_{i}p_{j}(1-F_{I T})
</math>
其中,i 和 j 代表 A 基因座上的不同等位基因,而 <math display="inline">F_{IT}</math> 衡量了基因型频率因群体内的非随机交配和群体间等位基因频率分化而完全偏离随机交配预期值的总偏离程度(National Research Council, Commission on DNA Forensic Science 1996)。若群体内为随机交配(<math display="inline">F_{IS}=0</math>),则 <math display="inline">F_{IT}</math> 在这两个方程中等同于 <math display="inline">F_{ST}</math>。此时,应用这些校正会以群体间等位基因频率分化的程度为比例,增加纯合子频率并降低杂合子频率。
在章节2.4中,三基因座DNA图谱的预期频率是基于哈迪-温伯格和随机交配的假设确定的。让我们回到该例,调整预期基因型频率和几率比以补偿人类群体中的群体结构。基于人类群体中 <math display="inline">F_{ST}=0.05</math> 的上限估计值,表4.8给出了调整后的预期基因型频率。校正后,两个杂合基因座的预期频率降低,而纯合基因座的预期频率增加。在随机交配假设下,该三基因座基因型的随机匹配几率比为1/20,408;校正群体结构后变为1/15,152。因此,群体结构使该三基因座基因型的预期频率比随机交配预期值增加了约35%。校正群体结构后,该三基因座基因型的随机匹配概率更高。在确定DNA图谱的几率比时,必须考虑群体结构以准确估计仅凭偶然性匹配DNA图谱的频率(National Research Council, Commission on DNA Forensic Science 1996)。当缺乏合适的参考等位基因频率数据库、个体种族未知、或基因型来自混合祖先个体(因而难以选择合适数据库)时,需使用式4.49和4.50进行群体结构校正。
问题框4.3 群体结构对DNA图谱匹配概率的影响
回到章节2.4和问题80×2.1,确定校正人类群体中观察到的群体结构后的预期基因型频率和随机匹配概率。假设人类群体的 <math display="inline">F_{ST}=0.05</math>。当存在群体结构时,单个基因座的预期基因型频率如何变化?为什么?10基因座基因型是否仍足够稀有,使得随机匹配的几率较低?
表4.8 校正与未校正群体结构的单个DNA图谱基因座及三基因座组合的预期频率。计算假设 <math display="inline">\bar{F}_{IS}=0</math>,并使用人类群体中 <math display="inline">\bar{F_{ST}}=0.05</math> 的上限估计值。等位基因频率见表2.3。
<table><tr><td></td><td colspan="2">预期基因型频率</td></tr><tr><td>基因座</td><td>随机交配</td><td>存在种群结构</td></tr><tr><td>D3S1358</td><td>2(0.2118)(0.1626) = 0.0689</td><td>2(0.2118)(0.1626)(1-0.05) =0.0655</td></tr><tr><td>D21S11</td><td>2(0.1811)(0.2321)=0.0841</td><td>2(0.1811)(0.2321)(1-0.05)=0.0799</td></tr><tr><td>D18S51</td><td>(0.0918)²=0.0084</td><td>(0.0918)²+ 0.0918(1-0.0918)(0.05) =0.0126</td></tr><tr><td>所有基因座</td><td>(0.0689)(0.0841)(0.0084)=0.000049</td><td>(0.0655)(0.0799)(0.0126)=0.000066</td></tr></table>
下一节将探讨用于推断特定种群结构模式成因的种群结构模型。
#### 4.6 预测种群结构模式的演化模型
无限岛屿模型与有限岛屿模型。踏脚石模型与集合种群模型。
• 距离隔离机制
基因流的最小成本路径与抗性隔离机制
不同迁移模型的通用预测与结论
使用$F_{ST}$(或其估计量)估算种群间遗传分化的重要目标,是推断导致观察到的遗传分化模式的种群遗传过程。这一关键步骤需要能预测遗传漂变和基因流速率的预测模型,从而预测$F_{ST}$的模式和量级。基于这些预测,即可通过实际种群中$\hat{F}_{ST}$的观测值来推断与基因流和遗传漂变相关的参数。
现有多种种群结构模型试图近似真实种群中可能存在的各种基因流模式。然而,这些模型未必能完全捕捉真实种群中基因流特征的精确组合。事实上,真实生物亚种群内部和之间的基因流很可能不像这些模型假设的那样易于分类或恒定不变。尽管如此,这些种群结构模型仍是研究导致种群分化的基本原理的有用工具。这些不同种群结构模型的实用性在于,它们能展示基因流速率、亚种群规模、亚种群间遗传连通模式对种群内和种群间基因型和等位基因频率演化的基本且具有一定普适性的影响特征。
#### Infinite island model
在亚种群间基因流动过程的模型中,最古老且应用最广泛的是Wright(1931,1951)提出的无限岛屿模型。该模型中,所有亚种群与其他任何亚种群交换迁移个体的概率均等,即完全不存在距离隔离效应。此外,通常假设各亚种群的规模与迁移率相同。整个种群由无限个亚种群组成,每个亚种群的有效大小为<math display="inline">N_{e}</math>,每代有<math display="inline">m</math>比例的基因拷贝随机与种群其他部分交换(见图4.5)。利用该模型,可近似建立亚种群间分化程度与有效种群大小及迁移量的函数关系。
无限岛屿模型:一种理想化的种群分化和基因流动模型,假设存在无限个相同的亚种群(繁殖群),且每个亚种群接受来自其他所有亚种群基因流动的概率均等。
首先考虑无限岛屿模型中无基因流动时(<math display="inline">m=0</math>)的情况。由于每个亚种群均为有限岛屿,等位基因频率会因遗传漂变而发生代际波动。亚种群相对于总种群的固定指数期望值为:
<math display="block">
F_{S T}=1-e^{-\frac{1}{2N e}t}
</math>
其中<math display="inline">t</math>为世代时间,<math display="inline">N_{e}</math>为单个亚种群的有效大小(Wright 1943a)。方程中,随时间增长,<math display="inline">e^{-\frac{1}{2N e}t}</math>项随有效种群大小递减。这近似描述了<math display="inline">F_{S T}</math>随<math display="inline">t</math>增加的变化趋势——亚种群的平均期望杂合度(<math display="inline">H_{S}</math>)降低并最终趋于零,导致<math display="inline">F_{S T}</math>趋近于1。这是遗传漂变使所有亚种群最终达到固定或丢失的结果。需注意,总种群杂合度(<math display="inline">H_{T}</math>)不受遗传漂变影响,因尽管单个亚种群可能固定或丢失,但无限亚种群使总种群规模趋于无限。
接下来考虑基因流动与遗传漂变同时作用的无限岛屿模型。第3章中,单个有限种群的基因型中两个等位基因为自体受精或同源的概率测度——固定指数:
<math display="block">
F_{t}=\frac{1}{2N_{e}}+\biggl(1-\frac{1}{2N_{e}}\biggr)F_{t-1}
</math>
当存在多个经历有限基因流动的亚种群时,可将此方程扩展至包含迁移对自体受精的影响。目标是建立同时考虑种群大小与迁移的固定指数表达式。有限种群规模导致各亚种群内自体受精率随时间递增,而迁移通过引入非同源等位基因降低自体受精率。因此,在分群种群中,净自体受精率是遗传漂变与迁移过程的动态平衡。
当存在基因流时,式4.52中给出的自交合概率需要进行两处修正。第一处修正涉及自交合概率<math display="inline">\frac{1}{2N_{e}}</math>。在迁移存在的情况下,亚种群中某个比例<math display="inline">m</math>的等位基因通过基因流从其他亚种群迁入,而<math display="inline">1-m</math>比例的等位基因由未离开原种群的个体和配子贡献。因此,存在一定概率使得一对等位基因中的一个或两个是通过迁移引入亚种群的。
在存在基因流的情况下,亚种群中随机抽样的一对等位基因可能包含零个、一个或两个迁入等位基因,其概率分别为<math display="inline">\left(1-m\right)^{2}</math>、<math display="inline">2m(1-m)</math>和<math display="inline">m^{2}</math>。只有不包含迁入等位基因的基因型(占比<math display="inline">(1-m)^{2}</math>)才能通过有限抽样形成同源相同的等位基因池。这也可以通过观察得出:每个世代预计有<math display="inline">2m(1{-}m)</math>的杂合基因型和<math display="inline">m^{2}</math>的纯合基因型携带迁入等位基因。这两类携带迁入等位基因的基因型会将自交合率降低<math display="inline">1-2m(1-m)-m^{2}~=~1-2m+2m^{2}-m^{2}=(1-m)^{2}</math>倍。
因此,经基因流修正后的自交合率为<math display="inline">\frac{1}{2N_{e}}\left(1-m\right)^{2}</math>。同理,亚种群中随机抽样的一对等位基因因历史近亲交配形成自交合的概率(即式4.52中的<math display="inline">\left(1-\frac{1}{2N_{e}}\right)F_{t-1}</math>项)也需要乘以<math display="inline">\left(1-m\right)^{2}</math>的修正因子。
综合这两处修正可得:
<math display="block">
F_{t}=\frac{1}{2N_{e}}\left(1-m\right)^{2}+\left(1-\frac{1}{2N_{e}}\right)F_{t-1}\left(1-m\right)^{2}
</math>
该方程表明,当<math display="inline">m</math>在0到1之间时,基因流通过降低当前世代(时间<math display="inline">t</math>)和过去世代(时间<math display="inline">t-1</math>)的等位基因同源概率来减少固定指数的期望值。这符合直觉:若基因流将等位基因拷贝引入亚种群,则该拷贝尚未经历<math display="inline">t-1</math>到<math display="inline">t</math>时间段的抽样过程,因此在时间<math display="inline">t</math>时无法通过同源相同性影响自交合基因型的频率。
式4.53量化了多个亚种群间基因流与遗传漂变的平衡关系,此时<math display="inline">F</math>等同于<math display="inline">F_{S T}</math>。通过将其应用于无限岛屿模型,当遗传漂变引起的亚种群间等位频率分化与基因流引起的亚种群间等位频率均质化达到平衡时,可以得到群体间固定指数<math display="inline">F_{S T}</math>的期望值。假设迁移率远小于有效种群规模(见数学框4.1),无限岛屿模型平衡状态下亚种群间固定程度的近似解为:
<math display="block">
F_{S T}\approx\frac{1}{4N_{e}m+1}
</math>
该结果由Wright(1931,1951)提出。
数学框4.1 The expected value of <math display="inline">F_{S T}</math> in the infinite-island model
当遗传漂变的差异化效应与基因流的均质化效应达到平衡时,<math display="inline">F_{S T}</math>的值在世代间不再变化,即<math display="inline">F_{S T(\mathrm{t})}=F_{S T(t-1)}=F_{S T(e q u i l i b r i u m)}</math>。若种群处于平衡状态,则可将<math display="inline">F_{t}</math>和<math display="inline">F_{t-1}</math>均设为<math display="inline">F_{e q}</math>。将此代入式4.53:
<math display="block">
F_{e q}=\frac{1}{2N_{e}}\left(1-m\right)^{2}+\left(1-\frac{1}{2N_{e}}\right)F_{e q}\left(1-m\right)^{2}
</math>
该方程可通过重写为以下形式更清晰地求解<math display="inline">F_{e q}</math>:
<math display="block">
F_{e q}=a c+b c F_{e q}
</math>
其中<math display="inline">a=\frac{1}{2N_{e}},b=1-\frac{1}{2N_{e}},</math> 且<math display="inline">c=(1-m)^{2}</math>。通过代数变换可得:
<math display="block">
\begin{array}{l}{{F_{e q}-b c F_{e q}=a c}}\\
{{{F_{e q}}(1-b c)=a c}}\\
{{{F_{e q}}=\displaystyle\frac{a c}{1-b c}}}\end{array}
</math>
将<math display="inline">a,b,</math>和<math display="inline">c</math>的完整表达式代入后得到:
<math display="block">
F_{e q}=\frac{\displaystyle\frac{1}{2N_{e}}\left(1-m\right)^{2}}{1-\left(1-\frac{1}{2N_{e}}\right)\left(1-m\right)^{2}}
</math>
将该式乘以<math display="inline">\frac{2N_{e}}{2N_{e}}</math>可简化为:
<math display="block">
F_{S T}=\frac{(1-m)^{2}}{2N_{e}-(2N_{e}-1){(1-m)}^{2}}
</math>
分子和分母的项展开后会产生较为复杂的表达式(若感兴趣可自行展开)。然而,若再次假设迁移率极小且远小于有效种群大小,则式4.61展开后含<math display="inline">m</math>或其幂次的项可忽略(例如,当<math display="inline">m=0.01</math>时,<math display="inline">2m=0.02</math>且<math display="inline">m^{2}=0.0001</math>)。由此可得固定指数的期望值近似为:
<math display="block">
F_{S T}\approx\frac{1}{4N_{e}m+1}
</math>
基于这些假设,图4.15展示了在无限岛屿模型中,不同有效种群大小与迁移率乘积<math display="inline">\left(N_{e}m\right)</math>下各亚种群间遗传分化的预期水平。当<math display="inline">N_{e}m</math>(常称为有效迁移率)较大时,二倍体位点的亚种群间分化极低,因为有效种群大小与迁移率的组合足以抵消遗传漂变引起的分化。当有效迁移率从较大值(如<math display="inline">N_{e}m=10</math>)下降时,亚种群间遗传分化最初缓慢增加,一旦有效迁移率低于约1时则迅速上升。每两代迁移一个个体的有效迁移率<math display="inline">\begin{array}{r}{(N_{e}m=\frac{1}{2N_{e}})}\end{array}</math>常被认为足以在无限岛屿模型中防止二倍体位点出现显著遗传分化,因为该速率基本能抵消孤立种群中遗传漂变导致的杂合度损失速率<math display="inline">(1-\frac{1}{2N_{e}})</math>(见第3.4节)。
亚群等位基因频率、杂合度的层级度量与固定指数之间的关系,可通过分划种群中基因流与遗传漂变的模拟得以体现(图4.16)。当基因流相对较强并维持亚群间等位基因频率相似时,亚群期望杂合度与总种群期望杂合度也相近,导致固定指数值较低(图4.11A)。当基因流较弱且亚群间等位基因频率发生分化时,亚群期望杂合度将低于总种群的期望杂合度,从而导致固定指数值升高(图4.11B)。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/123076c63361c37121ce0a5527f69813ae33ed578391616251f33192c5b8e964.jpg
图4.15 在无限岛屿种群结构模型中,亚群间固定程度的期望水平取决于有效种群大小<math display="inline">\mathrm{(N_{e})}</math>与基因流量(m)的乘积。每条曲线代表具有不同自合概率位点的期望<math display="inline">\mathrm{F}_{\mathrm{ST}}</math>(自下而上依次为<math display="inline">\frac{1}{2N_{e}},\frac{1}{N_{e}}</math>和<math display="inline">\frac{2}{N_{e}}</math>)。当<math display="inline">\mathrm{N_{e}m}</math>低于1时,对于自合概率为<math display="inline">\displaystyle\frac{1}{2N_{e}}</math>的双亲遗传核基因座,预期会出现显著的等位基因频率分化<math display="inline">(\mathrm{F_{ST}}\ge 0.2)</math>。Y染色体或线粒体基因座(自合概率<math display="inline">=\frac{2}{N_{e}}</math>)则表现为在较高<math display="inline">\mathrm{N_{e}m}</math>水平下仍会出现显著的种群间分化。
另需注意的是,<math display="inline">F_{ST}</math>在从相同亚群以相同方式抽样的独立重复基因座间可能存在显著变异。图4.17展示了在有限岛屿模型中,通过1000个独立基因座模拟遗传漂变与基因流(无突变)对等位基因频率改变时获得的<math display="inline">F_{ST}</math>值范围。在相同种群遗传过程作用下,单个基因座<math display="inline">F_{ST}</math>值的变异范围源于遗传漂变的随机性。每个基因座经历的等位基因频率随机波动,导致了亚群间等位基因频率方差的差异。模拟中由遗传漂变引起的<math display="inline">F_{ST}</math>随机变异强调:对<math display="inline">F_{ST}</math>的估算必须基于多个基因座的平均值。
固定指数与有效迁移个体数之间的预期关系依赖于无限岛屿模型,这主要有两个原因。首先,在岛屿模型中,所有亚种群从其他所有种群迁入的速率相同,因此仅存在一个适用于所有亚种群的单一迁移率<math display="inline">(m)</math>。其次,由于存在无限数量的亚种群,整个集合种群永远不会因遗传漂变达到固定或丢失状态。在具有有限数量亚种群的基因流岛屿模型中(称为有限岛屿模型),整个种群集合最终会达到固定或丢失状态,且<math display="inline">F_{S T}</math>最终会下降至零——因为在无突变情况下,所有亚种群最终会因遗传漂变达到固定或丢失(Nei et al. 1977; Varvio et al. 1986)。有限岛屿模型中,对于具有任意等位基因数的位点,遗传分化的预期程度为:
<math display="block">
G_{S T}\approx{\frac{1}{\left({\frac{d}{d-1}}\right)^{2}4N_{e}m+1}}
</math>
其中<math display="inline">d</math>为亚种群数量(Latter 1973; Takahata 1983; Crow and Aoki 1984; Takahata and Nei 1984)。此版本的<math display="inline">G_{S T}</math>修正了有限亚种群数量下亚种群间分化的预期程度。项<math display="inline">\left(\frac{d}{d-1}\right)</math>在具有两个亚种群时达到最大值4,并随着<math display="inline">d</math>增大趋近于1。例如,当<math display="inline">N_{e}m=0.1</math>且<math display="inline">d=10</math>时,<math display="inline">G_{S T}</math>的期望值约为无限数量亚群预期值的94%。这表明,相较于极多亚种群的情况,特定水平的基因流在较少亚种群间实现等位基因频率同质化的效果略高。当<math display="inline">d</math>大于约50时,有限亚群数量的修正影响甚微,此时有限亚群数量的行为本质上与无限亚群数量模型一致。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/271b67678a3148ce4bfb28b274bf6a66216a838200cfb232568d6c0470a31611.jpg
图4.16 有限岛屿模型模拟的等位基因频率、层级杂合度及固定指数。每个亚种群包含10个个体。面板A中基因流速率<math display="inline">m=0.2</math>,面板B中<math display="inline">m=0.01</math>。等位基因频率显示的是模拟中200个亚种群随机选取的6个亚种群数据。杂合度与固定指数由全部200个亚种群计算得出。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/ea308117730cd030ebd754be14193b0a0026163fc10b2dd62b20677e90acaeef.jpg
图 4.17 在包含200个亚群的有限岛屿模型中,1000个中性位点重复的<math display="inline">F_{S\mathrm{T}}</math>值分布。每个亚群包含10个个体,基因流率为每个亚群的10%(<math display="inline">m=0.10</math>)。分布中,95%的重复位点显示<math display="inline">F_{\mathrm{ST}}</math>值介于0.1459和0.2002之间,而所有1000个重复位点的平均值为0.1586(基于<math display="inline">\cdot{{H}_{T}}</math>和<math display="inline">H_{S}</math>的平均值计算<math display="inline">F_{\mathrm{ST}}</math>)。重复位点展现出<math display="inline">F_{\mathrm{ST}}</math>值的范围,因为亚群间的等位基因频率部分源自遗传漂变的随机过程。在<math display="inline">N_{e}m=1.0</math>的无限岛屿模型中,<math display="inline">F_{\mathrm{ST}}</math>的期望值为0.2。
问题框 4.4 Y染色体和细胞器基因座的<math display="inline">F_{S T}</math>预期水平
<math display="block">
N_{e}m\approx\frac{1}{4}\left(\frac{1}{F_{S T}}-1\right)
</math>
在岛屿模型中,Y染色体基因座或线粒体和叶绿体(细胞器)基因座的平衡状态下<math display="inline">\boldsymbol{F}_{S T}</math>的期望值是多少?解决此问题的提示是思考非二倍体常染色体的自合子性(autozygosity),然后对式 4.53 进行调整以推导出式 4.54 的不同版本。与双亲遗传的二倍体基因座相比,这些类型基因座的群体间固定水平<math display="inline">(F_{S T})</math>预期如何?导致不同类型基因座<math display="inline">\bar{F}_{S T}</math>水平差异的原因是什么?
该方程用于在无限岛屿模型中,根据亚群间的遗传分化程度推导预期有效迁移率。它再次强调:亚群间等位基因频率分化水平<math display="inline">(F_{S T})</math>是基因流(倾向于使亚群间等位基因频率均质化)与遗传漂变(导致亚群在个体趋近固定或丢失过程中分化)在<math display="inline">N_{e}m</math>背景下动态平衡的函数。该关系已被广泛应用于数千项研究中,通过表 4.9 中的案例,从野生群体<math display="inline">\hat{F}_{S T}</math>的经验估计值来估算<math display="inline">\hat{N_{e}m}</math>。该方程(或基于不同种群模型的类似期望)是所谓的间接估计有效迁移数<math display="inline">(\hat{N_{e}}m)</math>的基础,这些迁移数导致了群体间等位基因频率分化的特定模式<math display="inline">(\hat{F}_{S T})</math>。
需要认识到的是,使用式4.64估算<math display="inline">\widehat{N_{e}m}</math>本质上是将无限岛屿模型作为理想标准,而非实际估算特定群体的长期有效迁移个体数。由于这种对无限岛屿模型的依赖,通过<math display="inline">\hat{F}_{S T}</math>获取<math display="inline">\widehat{N_{e}m}</math>的估计值应解释为:“观测到的群体分化水平<math display="inline">(\widehat{F}_{S T})</math>将等同于在给定有效迁移个体数<math display="inline">(N_{e}m)</math>的无限岛屿模型中预期的分化水平。”这种实际群体与理想群体的比较方式与有效群体大小的定义完全一致(见第3.3节)。尽管高度依赖理想化模型,Slatkin和Barton(1989)得出结论:即使实际群体结构与岛屿模型存在偏差,在岛屿模型假设下使用观测的群体分化水平来估算<math display="inline">\widehat{N_{e}m}</math>仍大致准确。相反,Whitlock和McCauley(1999)综述了实际群体偏离无限岛屿模型的多种方式,以及用于近似<math display="inline">\hat{F}_{S T}</math>与<math display="inline">N_{e}m</math>关系的假设条件,指出式4.64的滥用是不合理的。
鉴于无限岛屿模型可推导出特定有效迁移率水平下繁殖群间的预期遗传分化水平,将这一关系逆向应用是自然的:
互动框4.5 有限岛屿模型中<math display="inline">F_{1S},F_{S\top},</math>和<math display="inline">{\cal F}_{\mathrm{IT}}</math>的模拟
使用教材配套模拟网站探究有限数量亚群间的岛屿模型基因流。首先查看各模拟输入参数。以默认参数运行模拟并观察四个输出图表,注意各图的坐标轴和绘制曲线。
分别用以下有效群体大小、迁移率和初始等位基因频率值运行模拟。每种情况下<math display="inline">N_{e}m</math>是多少?
| Ne
|
m
|
初始等位基因频率 p
|
| 10
|
0
|
0.5
|
| 10
|
0.001
|
0.5
|
| 10
|
0.1
|
0.5
|
| 50
|
0
|
0.5
|
| 50
|
0.001
|
0.5
|
| 50
|
0.1
|
0.5
|
| 100
|
0
|
0.5
|
| 100
|
0.001
|
0.5
|
| 100
|
0.1
|
0.5
|
每次模拟运行时,观察亚群样本中随时间变化的等位基因频率、层级杂合度指标<math display="inline">(H_{I},H_{S},</math>和<math display="inline">H_{T})</math>以及固定指数<math display="inline">(\tilde{F}_{I S},\tilde{F}_{S T},</math>和<math display="inline">\bar{F}_{I T})</math>。当等位频率曲线偶尔触及顶部或底部坐标轴(达到固定或丢失)后又重新出现时,这现象说明了什么?共祖系数如何定义?它与亚群内杂合度及<math display="inline">\bar{F}_{15}</math>有何关联?
你在模型参数框中输入的迁移值单位是什么?为什么增加<math display="inline">m</math>会维持较低的<math display="inline">F_{ST}</math>和<math display="inline">\bar{F}_{IT}</math>值?迁移如何抵消遗传漂变?迁移是否总能强大到克服遗传漂变的分化效应?
表4.9 基于核位点分子遗传标记数据估算的不同物种亚群间固定指数(<math display="inline">F_{ST}</math>)。根据遗传标记类型和研究设计采用了不同估算方法。每个<math display="inline">\boldsymbol{F}_{ST}</math>估值被用于推断在无限岛屿模型假设下会产生相同种群结构水平的有效迁移个体数(<math display="inline">N_em</math>)。
| Species
|
FST estimate
|
Nem estimate
|
References
|
| Amphibians
|
|
|
|
| Alytes muletansis (Mallorcan midwife toad)
|
0.12-0.53
|
1.8-0.2
|
Kraaijeveld-Smit et al. (2005)
|
| Birds
|
|
|
|
| Gallus gallus (broiler chicken breeds)
|
0.19
|
1.0
|
Emara et al. (2002)
|
| Mammals
|
|
|
|
| Capreolus capreolus (roe deer)
|
0.097-0.146
|
2.2-1.4
|
Wang and Schreiber (2001)
|
| Homo sapiens (humans)
|
0.03-0.05
|
7.8-4.6
|
Rosenberg et al. (2002)
|
| native Mexican populations
|
0.136
|
1.6
|
Morena-Estrada et al. (2014)
|
| European and Chinese
|
0.11
|
2.0
|
Altshuler et al. (2010)
|
| Microtus arvalis (common vole)
|
0.17
|
1.2
|
Heckel et al. (2005)
|
| Plants
|
|
|
|
| Arabidopsis thaliana (mouse-earcress)
|
0.643
|
0.1
|
Bergelson et al. (1998)
|
| Oryza officinalis (wild rice)
|
0.44
|
0.3
|
Gao (2005)
|
| Phlox drummondi (annual phlox)
|
0.17
|
1.2
|
Levin (1977)
|
| Prunus armeniaca (apricot)
|
0.32
|
0.5
|
Romero et al. (2003)
|
| Fish
|
|
|
|
| Morone saxatilis (striped bass)
|
0.002
|
11.8
|
Brown et al. (2005)
|
| Sparisoma viride (stoplight parrotfish)
|
0.019
|
12.4
|
Geertjes et al. (2004)
|
| Insects
|
|
|
|
| Drosophila melanogaster (fruit flies)
|
0.037-0.063
|
3.7-6.5
|
Fabian et al. (2012)
|
| Glossina pallidipes (tsetse flies)
|
0.18
|
1.1
|
Ouma et al. (2005)
|
| Heliconius charithonia (butterflies)
|
0.003
|
79.8
|
Kronforst and Flemming (2001)
|
| Corals
|
|
|
|
| Seriatopora hystrix
|
0.089-0.136
|
2.6-1.6
|
Maier et al. (2005)
|
通过岛屿模型获得的迁移有效数量估计值(<math display="inline">\hat{N_{e}m}</math>)被称为基因流率的间接估计。使用“间接”这一术语,是因为亚种群间等位基因频率差异的观测模式被用于一个模型(包含许多假设)中以生成参数估计值。这与通过亲本分析(parentage analysis)等方法直接估计基因流形成对比(尽管第4.2节指出直接方法也依赖于假设)。这类基因流的间接估计会对所有导致当前亚种群间等位基因频率分化格局的历史事件进行平均化处理。相比之下,直接估计仅适用于观察到亲本关系或迁移行为的时间段。Slatkin(1987a)曾研究过一个案例:标记-重捕获(mark–recapture)方法显示某蝴蝶在不同地理区域间的迁移极为有限,但基于多基因座估计的<math display="inline">\hat{F}_{ST}</math>却表明该蝴蝶种群间几乎没有等位基因频率分化。一种可能的解释是,过去基因流非常频繁,而近期急剧减少,但尚未经历足够时间以观察到种群分化增强。另一种可能性是,标记-重捕获技术未能有效检测到维持种群不分化的低频基因流事件。
阶石模型与集合种群模型
受日本庭园中铺路石板启发而提出的阶石模型(stepping-stone model),通过限制大多数或全部基因流仅发生在相邻亚种群之间(Kimura 1953;见图4.5),近似模拟了离散亚种群间因距离产生的隔离现象。这种基因流模式在亚种群间产生的等位频率聚集效应,与本章第一节描述的连续分布个体群体中因距离隔离产生的效应在性质上极为相似(图4.3)。Kimura和Weiss(1964)对阶石模型进行了经典分析,他们证明:从两个亚种群中随机抽样获得的等位状态相关性取决于(i)两个被采样亚种群间相隔的亚种群数量,以及(ii)相邻群体间基因流与随机距离亚种群间长距离基因流的比例。正如距离隔离所预期的,等位状态相关性随亚种群间距离增加而降低。有趣的是,当亚种群分布于二维空间时,等位状态相关性随距离下降的速度比一维分布时更快。在二维阶石模型中,当基因流参数固定时,<math display="inline">F_{ST}</math>预计随群体数量的对数增长(见Slatkin和Barton 1989;Cox和Durrett 2002)。换言之,随着群体数量增加,维持相同种群结构水平所需的基因流强度也需相应增强。
对踏脚石模型(stepping-stone model)的逻辑扩展是集合种群模型(metapopulation model)。集合种群模型不仅模拟基因流动过程,还近似描述了自然种群中常见的持续灭绝与再定居现象。这类模型的灵感来源于先锋植物和树木等生物——它们在新形成的林窗中定居生长,但随着演替引入新物种并改变环境和竞争条件,最终会从某个斑块中消失。尽管先锋物种的每个亚种群最终都会灭绝,但在任意给定时间点仍有其他亚种群存在,且通过定居过程不断形成新的亚种群。因此,集合种群可视为多个较小亚种群或栖息地斑块的集合(关于集合种群及相关概念的不同定义,参见Hanski和Simberloff 1997),其概念与踏脚石模型相似。然而在集合种群中,单个亚种群存在一定灭绝概率,这些空出的位置可被重新殖民以建立新亚种群。
集合种群中的基因流动可建模为两种类型:一类是现存被占据亚种群间的基因流动(类似岛屿模型);另一类发生在灭绝亚种群被新殖民取代时。殖民过程中基因流动的模式可能呈现不同形式(Slatkin 1977):第一种形式是所有亚种群中随机抽取殖民者,称为迁移库基因流(migrant-pool gene flow);第二种形式是从单一随机亚种群中抽取殖民者,称为繁殖体库基因流(propagule-pool gene flow)。迁移库基因流与岛屿模型的基因流动模式相同,迁移者代表所有亚种群的平均等位基因频率。相反,繁殖体库基因流在新亚种群建立时可能引发遗传瓶颈,因为殖民者仅来自单个现存亚种群。
殖民形式对集合种群内新建亚种群杂合度的影响可通过下式描述:
<math display="block">
F_{S T}^{c o l o n y}=\frac{1}{2k}+\phi\biggl(1-\frac{1}{2k}\biggr)F_{S T}
</math>
其中 <math display="inline">F_{S T}^{c o l o n y}</math> 是新建立亚种群中预期的等位基因频率分化,<math display="inline">k</math> 是二倍体拓殖者数量,<math display="inline">F_{S T}</math> 是现有亚种群间等位基因频率分化的程度,<math display="inline">\boldsymbol{\Phi}</math>(发音为”phi”)是新建立种群中两个等位基因拷贝来自同一亚种群的概率(Whitlock 和 McCauley 1990)。当 <math display="inline">\Phi=1</math> 时,colonization 对应于繁殖体库(propagule pool)(所有奠基等位基因拷贝均来自同一亚种群);当 <math display="inline">\boldsymbol\Phi=0</math> 时,对应于迁移库(migrant pool)(所有奠基等位基因拷贝来自不同亚种群)。由于从总种群中取样,所有新建亚种群都有机会通过血统同一性(identical by descent)建立等位基因,因此包含 <math display="inline">\textstyle{\frac{1}{2k}}</math> 项。对于通过繁殖体库建立的亚种群(即 <math display="inline">\Phi=1</math> ),等位基因因血统同一而纯合的概率会随着现有亚种群间等位基因频率分化的程度增加而升高。通过繁殖体库拓殖时,新建种群继承了现有亚种群的平均纯合度,加上来自有限种群取样的额外纯合度。通过迁移库拓殖时 <math display="inline">(\Phi=0)</math> ,奠基等位基因总是来自不同亚种群,因此杂合度与总种群杂合度(2pq)相同,仅存在有限拓殖者数量带来的取样误差。McCauley 等(1995)利用新建的 Silene alba 植物种群,估计 <math display="inline">\boldsymbol{\Phi}</math> 值在 0.73 至 0.89 之间,表明新种群在形成过程中确实经历了某些额外的取样过程,这些过程增加了种群分化。
在集合种群中,灭绝和再拓殖可能成为基因流的额外来源或额外限制(Maruyama 和 Kimura 1980;Wade 和 McCauley 1988)。对于所有二倍体拓殖者数量(k)的取值,繁殖体库拓殖都会增加整体种群分化。相反,迁移模型下整体分化的变化取决于现有亚种群间的基因流速率。当二倍体拓殖者数量(k)超过有效迁移个体数的两倍 <math display="inline">\left(2N_{e}m\right)</math> 时,分化趋于降低,因为拓殖实现了等位基因的额外混合。虽然 <math display="inline">F_{S T}</math> 是分化模式的有效度量指标,但其本身可能不足以有效估计经历灭绝和再拓殖的集合种群中的有效迁移率(Whitlock 和 Barton 1997;Pannell 和 Charlesworth 2000)。
Isolation by distance and by landscape connectivity
正如本章第一节所述,距离隔离被认为是许多种群中运行的基本过程。Rousset(1997)提出了一种相对简单的距离隔离模式检验方法,该方法已被广泛应用于实证研究。该检验依赖于所有亚种群对之间估计的<math display="inline">\hat{F}_{ST}</math>值,以及所有亚种群对之间的直线地理距离(即所谓的欧氏距离)估计值。在二维种群中,当存在距离隔离时,<math display="inline">\frac{\hat{F}_{ST}}{1-\hat{F}_{ST}}</math>(常称为线性化<math display="inline">\hat{F}_{ST}</math>)与地理距离对数的回归图预期具有正斜率。图4.18基于二维阶跃石种群模型的模拟数据展示了这种关系类型。Rousset(1997)证明这种回归线的斜率是繁殖个体密度和基因流距离方差的函数。遗传分化随距离增加的趋势也不强烈依赖于基因流分布或扩散核【dispersal kernel】的确切形状。
由于栖息地和景观具有物理异质性,且存在可能阻碍或促进基因流的多样化物种和群落组合,简单的亚种群间地理距离可能不是遗传分化的唯一原因。近期研究发展了一系列量化空间变异景观变量的方法,这些变量可能改变有效迁移率<math display="inline">\left(N_{e}m\right)</math>,从而与亚种群间的遗传分化存在因果关系。通过评估景观的连接性,定义栖息地区域并对其迁移或基因流发生能力进行评分,可生成摩擦表面或阻力表面,量化假设导致景观连接性变异的变量差异(Spear等,2010)。阻力表面可替代简单欧氏距离,用于检验分隔亚群落的景观特征与亚群落遗传分化之间的关系。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/7243837e7f51e195916c92fc9ee2e3509c057162764017031b053bb6e1fba494.jpg
图4.18 阶跃石模型中的亚种群对间遗传分化随地理距离增加而增强,符合距离隔离的预期。直线表示最小二乘法拟合结果。模拟数据使用IBDSim v2(Leblois等,2009)的二维阶跃石岛模型代际溯祖模型生成。网格为<math display="inline">10\mathrm{~x~}10</math>个亚种群(每个含50个体),具有吸收边界【absorbing boundaries】,局域迁移率为0.01,采用双等位基因的<math display="inline">k</math>等位基因模型,突变率为0.0005。图中数据采样自网格中心25个亚种群(每个采样10个体)。所有亚种群对间的<math display="inline">F_{ST}</math>使用在线Genepop(Rousset 2008b)进行估计。
两种利用景观信息来检验亚群遗传分化成因的模型是最优路径法(Adriaensen et al. 2003)和电路理论(McRae 2006; McRae et al. 2008,两种方法的比较参见Marrotte和Bowman 2017)。在这些模型中,采样亚群周围的景观被特征化为一系列假设会影响遗传连通性的变量。这些变量可包括降雨或降雪量、海拔、土壤类型、平均温度等物理属性,以及植被覆盖度、群落类型、捕食者密度或人类活动等生物变量。
最优路径是种群对之间基于景观属性假设基因流速率最大的单一通道。图4.19展示了一个假设的景观,该景观被划分为一系列栅格单元(由于景观的数字化图像称为栅格数据,因此这种网格称为栅格网格),其中每个栅格的基因流速率根据下方平面地图的特征进行估算。图4.18A中连接各对亚群的实线即为基于栅格评分的最优路径(总基因流速率最大)。最优路径法隐含一个假设:扩散个体或配子能够评估整个景观以找到具有最大连通性的单一通道,且不考虑多重可能路径。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/8b2a2f7fe74394867c3b428e02afae0dea8e65064bb7d3c2e07f5d24dec915df.jpg
图4.19 景观(由A和B下部平面的地形图表示)可被划分为栅格区域(称为栅格网格,因景观数字图像称为栅格数据),其中每对栅格的基因流连通性被评分(A和B的上部平面)。在此假设示例中,字母标记的节点代表亚群,栅格颜色越深表示基于景观变量的连通性越低。A图中虚线表示亚群间的欧氏距离,实线为亚群对间的单一最优路径(最大连通性与基因流)。B图中,所有栅格对间的连通性通过网状电路中的电阻器表示。电路中所有路径上各对亚群间的电压或电流类似于亚群间的净有效迁移率。C图展示了如何将所有亚群对的最优路径长度或电阻与线性化<math display="inline">F_{ST}</math>进行绘图。图中正斜率(实线)证明生成栅格评分的景观变量与亚群间遗传分化存在相关性。
数学框 4.2 通过电路分析预测景观基因流
另一种方法是考虑景观在亚种群之间提供了多条路径,每条路径的连接度可能不同。电路理论通过类比导线网络和电阻等电子元件中的电压或电流流动,模拟景观上多个位置之间的路径网络。图4.5展示了用于定义亚种群间”电阻”的最基本电路,其中亚种群间的有效迁移率连接被替换为电阻器。电阻距离是亚种群间有效迁移率概率的函数,而非地理距离的函数。
图4.18B展示了一个被划分为网格方块的假设景观。网格单元间的连接性通过每对方块间的电阻器表示,这些互连构成电路。电路中任意位置的电压或电流可通过电路分析方法求解。电路中的电阻、电压和电流可解释为节点的连接性,类似于大量个体沿电路定义的路径随机移动时所经过的路径。McRae等(2008)综述了电路理论,并举例说明了如何通过电导率、电阻(电导的倒数)、电流或电压建模不同电路形式,以预测亚种群间的遗传连通性。
一个简单示例可说明如何通过电路分析类比景观上亚种群间的基因流。电路由导体和电子元件连接的节点网络表示。图4.20展示了一个带编号节点和电阻器的电路,其中A和B代表两个类比亚种群的节点。电流在A和B间的流动会在电阻最低的路径达到最大,但电流将流经电路所有分支。节点3-5的导体通过电阻器接地,起到分流部分电流的作用,这类似于部分迁徙个体在穿越节点3时死亡的情况。
节点的属性(如电导或电压)可通过基尔霍夫电路定律(节点电流代数和为零;闭合回路电压代数和为零)和欧姆定律(电流=电压/电阻)进行预测。电路节点的电流或电压可表达为含多个未知数的方程组。
在节点1处,从B方向流入1A电流,流出电流量由含电阻器的两条导体上的电压差决定:
<math display="block">
1={\frac{V1-V3}{R1}}+{\frac{V1-V2}{R4}}
</math>
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/ff2861571d76cb25a6150822c1d26260cf6235aeaacdc3c3f6cf5c70b2cf68ed.jpg
图 4.20 用电阻器表示亚种群A和B间景观遗传连接的示例电路。
在节点2,电流从节点1的方向流入并向节点4流出。我们可以重复使用流经电阻4的电流表达式,并将其设为流经电阻5的流出电流,从而得到
<math display="block">
{\frac{V1-V2}{R4}}={\frac{V2-V4}{R5}}
</math>
在节点3,我们重复使用流经电阻1的电流表达式作为流入电流,并将其设为流向节点4和5的流出电流之和
<math display="block">
{\frac{V1-V3}{R1}}={\frac{V3-V4}{R3}}+{\frac{V3-V5}{R2}}
</math>
举例而言,设电阻值为 <math display="inline">{\mathsf{R}}1={\mathsf{R}}3=1</math>,<math display="inline">{\mathsf{R}}4={\mathsf{R}}5=2.</math>,以及 <math display="inline">\mathsf{R}2=20</math>。我们还利用连接到地的导体电压为零这一事实,确定V4和V5均为零。代入并简化后,得到三个方程与三个未知数:
<math display="block">
\begin{array}{c}模板:1=1.5V1-V3-0.5V2\ {{}}\ 模板:0=V2-0.5V1\ {{}}\ 模板:0=2.05V3-V1\end{array}
</math>
通过定义包含各变量系数的矩阵,并采用多种方法(如矩阵求逆或Cramer法则)求解这些线性方程的未知数(参见教材网页链接,该网站展示线性方程组的求解步骤)。电压解为 <math display="inline">\vee1=1.31</math>,<math display="inline">\lor2=0.66,</math> 和 <math display="inline">\sqrt{3}=0.64</math>。已知电压后,流经电阻R3到节点4的电流为V3/ <math display="inline">{\sf R}3=0.64</math>,流经电阻R5到节点4的电流为 <math display="inline">\scriptstyle\sqrt{2/{\mathrm{R}}5=0.66/2=0.33</math>,流经电阻R2到节点5的电流为V3/ <math display="inline">R2=0.64/20=0.032</math>。
回到A与B之间的遗传连通性,电路模型显示:33%的基因流沿路径1-2-4,64%沿路径1-3-4,而节点3处3.2%的基因流未成功。
McRae和Beier(2007)研究了线性化<math display="inline">F_{S T}</math>与地理距离、最低成本路径以及电路理论电阻之间的相关性,研究对象包括分布于中美洲的8个大叶桃花心木亚种群和北美西部的12个貂熊亚种群。两个物种的亚种群均被复杂景观和数百至数千公里的距离分隔。在两类物种中,使用电路理论表示景观基因流阻力的方法,比单纯地理距离更能强相关于亚种群对间的遗传分化。
景观方法在测试遗传分化原因时,倾向于采用这样一种视角:基因流是一个强烈的过程,而可能淡化遗传漂变速率在整个景观中的变化贡献——例如有效种群大小和基因流速率变化所预期的那样。尽管McRae(2006)已从有效迁移率(<math display="inline">N_{e}m</math>)的角度阐述了阻力和传导的概念,但这一观点依然存在。另一个挑战是,当前观察到的遗传分化实际上是历史过程在较长时间尺度上运作的记录。对于许多物种,我们可能预期亚种群间的遗传分化是景观连通性随时间变化的函数。因此,遗传分化与用于假设连通性的景观特征和生态变异通常不会在相似时间尺度上发生变化,这使得推断遗传分化原因更加困难。
遗传分化的不同起源种群。与其将采样位置作为先验的遗传群体证据,另一种方法是从基因型样本本身寻找证据以建立遗传群体,进而估计遗传分化。这类种群分配或聚类方法现已发展成熟,并被广泛用于经验性多位点基因型数据以推断遗传亚种群和估计遗传分化。传统上这些方法被分为基于模型的方法和基于统计估计的方法。基于模型的聚类方法依赖于明确的种群遗传模型以及对被采样种群作用过程的假设。基于统计估计的方法可用于确定遗传数据中的模式,从而将个体归入不同聚类。
混合(Admixture):在基因型分配方法的语境中,指通过杂交或历史上的基因流与交配,来自多个遗传分化种群的个体在其多位点基因型中发现的等位基因。不同位点可能表现出不同的种群起源,导致一个多位点基因型被分配不同比例的种群起源。
4.7 种群分配与聚类
• 最大似然分配
• 贝叶斯分配与聚类
• 经验性分配与聚类
当检测种群遗传分化时,个体通常从多个地理位点采样,这些位点随后作为比较基因型和等位基因频率差异的单位。然而,采样的地理单位可能无法很好地代表遗传种群单位。例如,分布于多个地理位点的个体可能属于同一遗传种群,而同一地理位点内的个体可能处于混合状态——最近来自
后验概率(Posterior probability):通过贝叶斯规则将先验概率与似然证据相结合后,赋予某个假设的概率。
概率(Probability):在指定模型下观察到某个结果的可能性。例如,在给定种群等位基因频率和Hardy-Weinberg模型时,特定基因型出现的概率。
最大似然分配
一种将基因型归源至其来源种群的方法,是通过计算基因型在已知等位基因频率的种群中,在特定交配模型下的期望频率。这将提供基因型(数据)的似然值,其中每个来源种群代表一种可能的起源(或具有等位基因频率作为参数值的模型版本)。我们将基因型分配给能产生该基因型最大生成似然值的来源种群(或模型版本)。为理解这种基于最大似然的种群归源方法的简化版本,假设存在两个双等位基因位点(称为位点A和位点B),且个体分布于两个已知等位基因频率的亚种群中。
在种群一中,等位基因频率为<math display="inline">p_{\mathrm{A}}=0.3</math>、<math display="inline">p_{\mathrm{a}}=0.7</math>、<math display="inline">p_{\mathrm{B}}=0.4</math>、<math display="inline">p_{\mathrm{b}}=0.6</math>;而在种群二中,等位基因频率为<math display="inline">p_{\mathrm{A}}=0.7</math>、<math display="inline">p_{\mathrm{a}}=0.3</math>、<math display="inline">p_{\mathrm{B}}=0.6</math>、<math display="inline">p_{\mathrm{b}}=0.4</math>。现考虑一个基因型为AABB的个体:基于其基因型,该个体应属于哪个种群?
在随机交配假设下,AABB基因型的期望频率为<math display="inline">\big({p_{\mathrm{A}}}^{2}\big)\big({p_{\mathrm{B}}}^{2}\big)</math>。因此,该个体来自两个种群的可能性各是多少?为确定这一点,需分别使用两个种群的等位基因频率计算基因型的期望频率。在种群一中,期望基因型频率为<math display="inline">(0.3)^{2}(0.4)^{2}=(0.09)(0.16)=0.0144</math>,而在种群二中为<math display="inline">(0.7)^{2}(0.6)^{2}=(0.49)(0.36)=0.1764</math>。由于这些期望概率可能非常小(例如由多位点组成的多基因座基因型),通常将其表示为自然对数或以<math display="inline">e</math>为底的对数。
AABB基因型的自然对数似然值在种群一中为<math display="inline">\ln(0.0144)=-4.24</math>,在种群二中为<math display="inline">\ln(0.1764)=-1.74</math>。最大似然法的统计学原理是选择能使观测数据的对数似然值最大化的参数值或分布作为最优估计。在此案例中,基于种群等位基因频率,将AABB基因型个体归源至种群二时对数似然值最大(对数似然值最接近零)。
要确定基因型最大似然群体分配的置信度,需要比较所有可能基因型在潜在起源群体中的似然分布。这些分布可通过模拟大量在随机交配(或其他交配模型)下可能观察到的基因型来生成,前提是已知群体等位基因频率(参见交互框4.6)。模拟的似然分布为对数似然值提供置信区间。若负对数似然值落在某群体的置信区间之外,则认为该基因型不太可能起源于该群体。在上述简单示例中,AABB基因型可能分配到任一群体,因其似然分布存在重叠,故对其起源为群体二的分配缺乏高置信度。一般而言,等位基因频率分化的群体,其对数似然分布的重叠程度会随着位点数量增加和每个位点等位基因数增多而减少。
最大似然分配法最初应用于加拿大北极熊群体(Paetkau et al. 1995),现已被大量实证研究采用。该方法在以下条件下最为有效:(i)等位基因频率的估计独立于待分配群体的基因型集合;(ii)群体间等位基因频率存在分化;(iii)每个潜在源群体的交配为随机且位点独立(或固定指数<math display="inline">(F)</math>与不平衡系数<math display="inline">(D)</math>被准确估计并纳入基因型频率期望值),从而确保期望基因型频率模型的准确性;(iv)存在大量多态位点,使得任何给定多位点基因型的期望频率极低,从而提高基因型独特性。关于似然分配功效与精度的模拟研究结果详见Paetkau et al. (2004)。
贝叶斯分配
贝叶斯统计推断现已被广泛应用于群体遗传学推论。贝叶斯定理以托马斯·贝叶斯牧师(Reverend Thomas Bayes,1701–1761)命名,其遗作…
交互框4.6 基因型分配与聚类
通过教材网站可获取的电子表格模型文件,展示了似然法与贝叶斯法的基因型分配,以及推断最优支持群体数量的贝叶斯方法。
“基因型似然”标签页中的模型允许为三个群体设定两个双等位位点的等位基因频率。基于这些频率,为每个群体生成随机基因型样本。计算每个随机基因型的自然对数似然值,并通过图表比较三群体的对数似然分布。修改等位基因频率可观察其对对数似然分布的影响。
“贝叶斯分配”标签页展示了将AABB基因型分配到三个潜在起源群体所需的全部贝叶斯计算步骤。修改等位基因频率和先验概率分布,可观察其对后验概率、多位点分配及三个潜在起源群体的比例分配的影响。
贝叶斯推断的K表提供了一个基于随机分配的启发式聚类方法,将六个双位点基因型分配到一个或两个集群中。这有助于理解聚类的基本原理,但未包含完整方法中的众多细节,例如等位基因频率的先验分布【“prior distributions”译为“先验分布”】,或基于等位基因频率估计的基因型集群分配迭代更新【“iterative updating”译为“迭代更新”】。用户可通过重新计算工作表对基因型进行重采样,也可更改六个基因型的池。
1763年,托马斯·贝叶斯(Thomas Bayes)首次提出了这一概念框架。独立地,皮埃尔-西蒙·拉普拉斯(Pierre-Simon Laplace)发展了相同思想,并于1774年用一个方程形式化地定义了在观察到组合事件或条件下的结果后某一事件的概率(见Stigler 1986)。贝叶斯定理基于似然性,通过将假设置于一个权衡观察证据与先验信念的语境中,并通过总概率进行归一化(见数学框4.2)。
我们通过一个示例说明如何用贝叶斯规则确定后验概率分布,从而将基因型AABB的个体分配到多个可能来源种群(已知等位基因频率)之一。表4.10给出了三个可能来源种群在A和B位点的等位基因频率。对于一个基因型和<math display="inline">K</math>个可能来源种群,贝叶斯规则可表述为:
<math display="block">
P(K\mid \text{genotype})={\frac{P(\text{genotype}\mid K)P(K)}{P(\text{genotype})}}
</math>
确定种群<math display="inline">K</math>是该基因型来源的后验概率需要方程右侧的三个量:
<math display="inline">P(K)</math>是各可能种群作为AABB来源的先验概率。本例中,三个种群被视为AABB个体的等可能来源,因此每个<math display="inline">K</math>的先验概率相等,为<math display="inline">1/K=1/3</math>。存在多种可能的替代先验概率分布。例如,先验概率可基于空间位置加权,使采样基因型地理位置更近的来源种群具有更高的先验概率。
<math display="inline">P(\text{genotype}|K)</math>是给定来源种群时基因型的似然。在随机交配下,AABB基因型的期望频率为<math display="inline">(p_{\mathrm{A}}^2)(p_{\mathrm{B}}^2)</math>。这与本节前文用于似然分配的计算相同。表4.中种群1的AABB基因型似然为<math display="inline">(0.5^2)(0.8^2)=0.16</math>。<math display="inline">P(\text{genotype})</math>是在任何来源种群中观察到AABB基因型的总概率。该总概率为各种群基因型似然与种群先验概率乘积之和,即<math display="inline">\sum_{K=1} P(\text{genotype}\mid K)P(K)</math>。先验概率在不同来源种群间可能不同,但总和恒为1。如表4.10所示,AABB基因型的总概率为<math display="inline">(0.16)(0.333)+(0.0196)(0.333)+(0.0256)(0.333)=0.0069</math>。将这三个量结合用于种群1作为AABB个体的来源,得到其后验概率为——
表 4.10 使用贝叶斯法则进行基因型群体归属的示例。两个双等位基因座A和B,以及三个可能的群体。基于贝叶斯法则确定的后验概率,将基因型为AABB的个体归属到起源群体。给定群体下基因型的条件概率基于随机交配的Hardy–Weinberg预期。均匀先验概率分布假设个体来自三个起源群体的可能性相等。若存在混合,两个单一位点基因型被归属到不同起源群体,导致对群体1和3的分数归属<math display="inline">(q_{i\uparrow}=q_{i3}=0.5)</math>。
| 等位基因频率
|
1
|
2
|
3
|
| P(A)
|
0.5
|
0.2
|
0.8
|
| P(a)
|
0.5
|
0.8
|
0.2
|
| P(B)
|
0.8
|
0.7
|
0.2
|
| P(b)
|
0.2
|
0.3
|
0.8
|
| 基因型AABB的条件概率
|
1
|
2
|
3
|
| 群体K)
|
(0.5)² = 0.25
|
(0.2)² = 0.04
|
(0.8)² = 0.64
|
| 群体K)
|
(0.8)² = 0.64
|
(0.7)² = 0.49
|
(0.2)² = 0.04
|
| 群体K)
|
(0.5)²(0.8)² = 0.16
|
(0.2)²(0.7)² = 0.0196
|
(0.8)²(0.2)² = 0.0256
|
| 先验概率P(群体K)
|
0.33
|
0.33
|
0.33
|
| 基因型AABB的概率
|
1
|
2
|
3
|
| P(G-A locus)
|
(0.25)(0.33) = 0.083
|
(0.04)(0.33) = 0.013
|
(0.64)(0.33) = 0.213
|
| P(G-B locus)
|
(0.64)(0.33) = 0.213
|
(0.49)(0.33) = 0.163
|
(0.04)(0.33) = 0.013
|
| P(G-多位点)
|
(0.16)(0.33) = 0.053
|
(0.0196)(0.33) = 0.007
|
(0.0256)(0.33) = 0.009
|
| 后验概率
|
1
|
2
|
3
|
| G-A locus)
|
<math display="inline">\frac{0.25×0.33}{0.083+0.013+0.213}=0.269</math>
|
<math display="inline">\frac{0.04×0.33}{0.083+0.013+0.213}=0.043</math>
|
<math display="inline">\frac{0.64×0.33}{0.083+0.013+0.213}=0.688</math>
|
| G-B locus)
|
<math display="inline">\frac{0.64×0.33}{0.213+0.163+0.013}=0.547</math>
|
<math display="inline">\frac{0.49×0.33}{0.213+0.163+0.013}=0.419</math>
|
<math display="inline">\frac{0.04×0.33}{0.213+0.163+0.013}=0.034</math>
|
| G-多位点)
|
<math display="inline">\frac{0.16×0.33}{0.053+0.007+0.009}=0.780</math>
|
<math display="inline">\frac{0.0196×0.33}{0.053+0.007+0.009}=0.096</math>
|
<math display="inline">\frac{0.0256×0.33}{0.053+0.007+0.009}=0.125</math>
|
<math display="block">
\frac{(0.16)(0.333)}{0.053+0.007+0.009}=0.780
</math>
如表 4.10 所示,归属到群体2或群体3的后验概率较低,因此最支持的推断是AABB个体起源于群体1。注意后验概率之和为1。
贝叶斯归属程序的最简版本假设个体基因型中所有位点均源自单一群体。
在假设所有位点均源自单一来源种群的前提下,表4.10中对基因型进行多位点分配到种群1的推断。贝叶斯分配方法还可考虑混合(admixture)的可能性,即由于历史上种群间个体的杂交和交配,单个体的多位点基因型中不同位点可能源自多个不同种群。在混合模型下,<math display="inline">q_{k}^{i}</math>表示个体<math display="inline">i</math>的多位点基因型中源自种群<math display="inline">k</math>的比例。表4.10展示了考虑混合的种群分配结果,在示例中,A位点基因型被分配到种群3,而B位点基因型被分配到种群1。
图4.21展示了贝叶斯混合聚类分析的完整案例。基于模拟的10个位点基因型数据,从四个地点各取样的20个个体被划分为四个集群。每个个体的多位点基因型中源自各集群的比例(<math display="inline">\overset{\cdot}{q_{k}^{i}}</math>,y轴显示)表明:前三个集群中仅有少数个体具有显著比例的近期混源祖先成分,这与因基因流缺乏导致的高水平遗传分化一致。相反,第四个集群中大多数个体的部分位点显示出近期与其他集群的祖先关联,这符合近期存在基因流和较低遗传隔离的预期。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/905ff44d8f569fb7dbeaf1d1ca81f1b6053243941d441cc6bd4f60a59eeed9ed.jpg
图4.21 使用STRUCTURE软件的混合模型(Pritchard et al. 2000),基于贝叶斯后验概率将个体聚类为四个种群。每个个体的条形图显示其被分配到四个集群的祖先比例。该图基于有限岛屿模型(共20个种群,<math display="inline">N_{e}m=0.1</math>且无突变)下模拟的10个双等位位点数据。四个种群取样后,经过100代演化,20个种群间观测到<math display="inline">G_{ST}=0.59</math>。
贝叶斯方法可扩展用于检验遗传数据支持的种群数量假设。这允许基于观测数据对最优支持种群数量进行假设检验,而非假设地理分布或其他标准代表遗传实体。该方法通过贝叶斯定理获得后验概率,其原理与前述基因型分配类似但有所改进。最优聚类是使观测基因型数据的后验概率最大化的<math display="inline">K</math>值和基因型分配方案。
第一步是设定可能群体或集群数量<math display="inline">K</math>的范围,从一到某个最大值。(一种可能性是使用采样地理位点的数量作为最大<math display="inline">K</math>。)然后将所有<math display="inline">N</math>个观测基因型随机分配到从一到<math display="inline">K</math>的各个集群中。例如,当<math display="inline">k=1</math>时,所有<math display="inline">N</math>个基因型都被分配到同一个集群;当<math display="inline">k=2</math>时,基因型被随机分配到两个各含<math display="inline">N/2</math>个体的集群,以此类推直到每个<math display="inline">K</math>值对应的<math display="inline">N/K</math>规模集群。
接着计算这些随机分配基因型集群的等位基因频率。在确定每个集群的等位基因频率后,基于给定<math display="inline">K</math>下基因型分配到集群的情况,计算每个基因型的后验概率以及所有基因型聚类配置的后验概率。
随后对每个<math display="inline">K</math>的集群分配进行微小调整:随机将部分基因型重新分配到不同集群(提出新的基因型-集群分配方案)。如果这种重新分配提高了后验概率,则保留新方案,否则维持前一步的分配。(马尔可夫链蒙特卡洛[Markov chain Monte Carlo, MCMC]方法中的Metropolis-Hastings算法或Gibbs采样等,可用于估计使后验概率最大化的参数值。)
通过多次重复这种基因型分配的随机调整生成新方案的过程,可以估计每个<math display="inline">K</math>对应的最大后验概率。实际推断<math display="inline">K</math>的完整模型比此处描述的更为复杂,包括等位基因频率的先验概率分布,以及通过迭代过程先估计集群等位基因频率再根据后验概率重新分配基因型等细节(Pritchard et al. 2000; Falush et al. 2003)。
具有最高基因型数据后验概率的聚类数<math display="inline">K</math>是将基因型最佳支持分配到种群中的方案。表4.11给出了将图4.16所示模拟基因型数据分组为1到6个聚类的平均后验概率。四个聚类<math display="inline">(k=4)</math>对基因型数据的概率最高,因此是最佳支持的聚类数。通过模拟,Evanno等(2005)表明,使用后验概率推断聚类规模受遗传标记类型和样本量的影响。他们建议利用基因型数据对数概率随<math display="inline">K</math>值变化的速率来推断最佳支持的聚类数(另见Verity和Nichols 2016)。混合模型在种群分配中表现出更强的稳健性(François和Durand 2010)。Kaeuffer等(2007)展示了由遗传漂变引起的背景配子不平衡如何影响种群聚类的推断。Wang(2017)通过模拟数据证明,程序Structure(Pritchard等 2000)中估计的<math display="inline">K</math>和个体分配结果依赖于模型参数,且可能需要极少使用的参数组合才能准确将个体分配到源种群。由于聚类方法缺乏显式的突变模型,其结果可能对突变模式以及过滤低频近期突变的数据敏感(Shringapure和Xing 2009;Linck和Battey 2019)。Janes等(2017)综述了大量估计<math display="inline">K</math>的研究,并讨论了贝叶斯聚类应用和解释中可能的缺陷。Lawson等(2018)揭示了遗传聚类如何导致种群历史推断错误,并提出评估拟合优度的方法。贝叶斯聚类的替代模型和算法变体已在可分析基因型数据的软件包中实现(例如Guillot等 2005;Corander等 2008;Jay等 2015)。
数学框4.3 贝叶斯定理
假设<math display="inline">A</math>和<math display="inline">B</math>是代表具有两个水平(如存在和不存在)的事件或条件的变量。目标是通过与变量<math display="inline">B</math>相关的信息来学习<math display="inline">A</math>某一水平的概率。<math display="inline">P(A\mid B)</math>是在<math display="inline">B</math>为真时事件<math display="inline">A</math>发生的条件概率,其等于
<math display="block">
P(A\mid B)={\frac{P(A\cap B)}{P(B)}}
</math>
<math display="block">
P(A\mid B)P(B)=P(B\mid A)P(A)
</math>
为确定给定<math display="inline">B</math>时<math display="inline">A</math>的条件概率,我们可以重新排列方程得到贝叶斯规则
<math display="block">
P(A\mid B)={\frac{P(B\mid A)P(A)}{P(B)}}
</math>
该式表明,给定<math display="inline">B</math>时<math display="inline">A</math>的概率等于<math display="inline">A</math>和<math display="inline">B</math>的联合概率(<math display="inline">A</math>与<math display="inline">B</math>的交集)除以事件<math display="inline">B</math>的概率。(注意,若<math display="inline">A</math>和<math display="inline">B</math>独立,则<math display="inline">P(A\cap B)=P(A)P(B)</math>,此时<math display="inline">P(A\mid B)</math>等于<math display="inline">P(A)</math>。)基于这一条件概率关系的重新排列,可得
<math display="block">
P(B\cap A)=P(A\mid B)P(B)
</math>
交换<math display="inline">A</math>和<math display="inline">B</math>的顺序后,同样可得
<math display="block">
P(A\cap B)=P(B\mid A)P(A)
</math>
由于<math display="inline">P(B\cap A)=P(A\cap B)</math>,我们将这些交集概率的定义代入后可得
其中 <math display="inline">P(A)</math> 和 <math display="inline">P(B)</math> 是 <math display="inline">A</math> 和 <math display="inline">B</math> 相互独立时的概率(称为边际概率)。<math display="inline">P(A)</math> 是在考虑任何关于 <math display="inline">B</math> 的信息之前的事件 <math display="inline">A</math> 概率,称为先验概率。<math display="inline">P(B\mid A)</math> 是给定 <math display="inline">A</math> 时 <math display="inline">B</math> 的条件概率或似然。<math display="inline">P(A\mid B)</math> 也是给定 <math display="inline">B</math> 为真时事件 <math display="inline">A</math> 发生的条件概率。<math display="inline">P(A\mid B)</math> 被称为后验概率,它是我们需要确定的概率。分母中的概率 <math display="inline">P(B)</math> 是所有 <math display="inline">B</math> 为真的可能结果的概率之和,有时称为归一化常数。例如,若 <math display="inline">A</math> 有两种观测状态——真(<math display="inline">A</math>)和假(<math display="inline">A^{\prime}</math>)——则 <math display="inline">P(B)=P(A\cap B)+P(A^{\prime}\cap B)=P(B\mid A)P(A)+P</math> <math display="inline">(B\mid A^{\prime})P(A^{\prime})</math>。这里假设 <math display="inline">P(B)</math> 不等于零。
表 4.11 展示了使用 STRUCTURE(Pritchard et al. 2000; Falush et al. 2003)估计的模拟数据(图 4.16)在 <math display="inline">K</math> 取 1 到 6 时各聚类自然对数后验概率值的分布。给定 <math display="inline">k</math> 时数据的后验概率是对每个 <math display="inline">k</math> 进行 10 次独立聚类估计的平均值。后验概率的最大值和平稳区均表明 <math display="inline">k=4</math> 是最优估计值。模拟基因型数据来自有限岛屿模型中 4 个种群(每个种群 20 个体)的 10 个双等位基因位点,参数为 <math display="inline">N_{e}m=0.02</math>、无突变、20 个总种群模拟 100 代。
| k
|
Posterior probability
|
| 1
|
-1026.6
|
| 2
|
-863.8
|
| 3
|
-688.7
|
| 4
|
-634.1
|
| 5
|
-656.4
|
| 6
|
-666.8
|
经验分配方法
给定从多个地点收集的多位点基因型数据集,可以使用多种统计方法来汇总遗传数据、进行统计检验或实现数据可视化。传统经验群体聚类方法通过估计样本中所有基因型间的遗传距离来实现。遗传距离通过量化个体间的等位基因相似性来反映血缘同源程度。聚类可通过以下步骤完成:首先估计个体间的遗传距离,然后将基因型分组以最小化组内遗传距离并最大化组间遗传距离(遗传距离将在第 5 章详细讨论)。这一过程具有挑战性,因为需要选择合适的遗传相似性度量和聚类流程,才能在缺乏遗传过程完整知识的情况下从数据中提取有意义的结构模式。
对于具有多个位点的遗传数据,高维度使得解释变得困难。主成分分析(PCA)是一种成熟的数学技术,广泛应用于具有许多潜在相关自变量的大型数据集(Pearson 1901;Hotelling 1933)。该技术通过原始变量的线性组合,创建数量更少的新变量(即坐标轴)。PCA轴是原始变量的加权和,每个变量的权重由其对新变量的贡献程度决定,这种系数称为载荷。定义新变量可消除原始变量间的相关性。新变量轴是正交的——即呈直角关系的向量——且为独立变量。新轴还按其解释原始数据变异量的程度排序,第一PCA轴解释的变异量最大。(熟悉线性代数的读者可将新变量视为原始数据的特征向量,其特征值的大小量化了该轴解释的方差量。线性代数概念入门可参考Otto和Day(2007)的著作。)
交互框4.7 主成分分析可视化
通过图示原始轴与新轴的关系,可以更直观地理解PCA。网络上有大量利用图形或模拟演示PCA的教程。本文配套网页提供了多个实用网络资源的链接。
PCA最初作为经验聚类技术被用于降低多位点多等位基因遗传数据集的维度(Menozzi等,1978)。短读长测序技术可对每个个体生成数千个单核苷酸多态性(SNP)位点,这进一步推动了PCA分析在降低维度和可视化群体间或地理区域间遗传变异中的应用,该方法在处理超大规模数据集时具有相对较快的计算速度。
遗传数据的PCA分析始于对每个基因型或单倍型的评分。对于具有两个等位基因的常染色体二倍体位点,设<math display="inline">\mathrm{G}(i,j)</math>表示个体i在位点j的基因型评分:AA基因型记为2,Aa记为1,aa记为0,以反映基因型中A等位基因的数量。基因型评分需通过以下步骤进行中心化处理:首先计算每个位点的平均评分
<math display="block">
\mu_{j}=\frac{\displaystyle\sum_{i=1}^{N}G(i,j)}{N}
</math>
然后将每个个体的基因型评分减去<math display="inline">\upmu_{j}</math>以使评分以均值为中心。接着用等位基因频率乘积的平方根(<math display="inline">p_{j}=\mu_{j}/2</math>)对中心化后的基因型评分进行标准化
<math display="block">
M(i,j)=\frac{G(i,j)-\mu_{j}}{\sqrt{p_{j}\big(1-p_{j}\big)}}
</math>
回想二项分布的标准差为<math display="inline">\sqrt{p_{j}\big(1-p_{j}\big)}</math>可知,这种转换使每个基因型得分等于该位点上所有基因型A等位基因平均数偏离的标准差数。(对于具有两个以上等位基因的位点,二倍体基因型数据通过以下方式编码:为每个位点发现的每个等位基因单独设置一列,并通过个体携带的各等位基因数量进行评分。当每个位点具有两个以上等位基因时,将跳过重新标度的除法步骤(参见Cavalli-Sforza等1994;Patterson等2006)。由于具有共同祖先的个体其基因型会共享血统相同的等位基因,对基因型数据进行主成分分析可以估计多个位点的联合共祖关系。)
图4.22展示了来自四个采样点(每个点20个个体)的模拟10个位点基因型数据的主成分分析前两个轴。前两个主成分轴解释了约<math display="inline">61\%</math>的基因型变异,每个群体的数据点显示出与遗传分化群体一致的聚类趋势。群体4的数据点分布最分散,许多点与其他三个群体的数据点混杂,表明该群体近期经历了基因交流。作为对比,图4.17的主成分分析基于与图4.16中贝叶斯混合聚类相同的基因型数据。
Becquet等(2007)使用78只普通黑猩猩和六只倭黑猩猩的310个多态微卫星位点基因型数据,对主成分分析和贝叶斯聚类进行了类似比较。他们同时使用贝叶斯聚类和主成分分析来检测黑猩猩的遗传群体,并寻找群体间杂交个体的证据。两种数据分析方法结果一致,表明存在三个黑猩猩遗传群体,并推断两个野生个体为近期杂交后代。
针对群体遗传数据的主成分分析,已有形式化的遗传分化统计检验方法和检测遗传分化统计功效的评估方法(Patterson等2006)。McVean(2009)证明主成分分析模式与谱系间平均溯祖时间相关,从而建立了主成分分析模式与群体遗传预测模型(如群体分化和基因流/混合过程)的关键联系。一个应用案例是:基于采样点等位基因频率的主成分分析所解释的总变异度,等同于<math display="inline">F_{S T}</math>的估计值(McVean 2009)。主成分分析属于多变量分析方法家族,可应用于遗传数据以检测群体结构、鉴定杂种或杂交事件、检验群体间近期交配证据,并在多种模型下识别空间遗传模式(如Jombart等2008;Jombart等2009综述;Frichot等2012;Francois和Waits 2015)。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/0262902bf33da65c66c6ba81991b51347303954c4f301e3b80b420e2f13ad593.jpg
图 4.22 基因型数据的主成分分析显示10个二倍体位点的种群聚类。前两个主成分轴共同解释了近<math display="inline">72\%</math>的遗传变异。种群在主成分轴上的分布模式与遗传分化一致。种群1的点与其他种群分离程度最小,表明近期存在基因流和祖先关联。该图基于与图4.16相同的数据——在有限岛屿模型下模拟的10个双等位位点数据,模型包含20个总种群,<math display="inline">N_{e}m=0.1</math>,100代后当从四个种群各采样20个个体时,20个种群间的<math display="inline">G_{ST}=0.59</math>。
4.8 种群结构对谱系分枝的影响
多盒中的虫群。
具有种群分组的溯祖事件时间。
样本配置。
两个同类群中等待时间的均值与方差。
在存在基因流的结构化种群中,谱系可在同类群间迁移。通过溯祖视角,当前采样的两个谱系在回溯时可能经历 coalescence(融合)或 migration(迁移)(图4.23)。确定结构化种群中 coalescence 时间的均值与方差将揭示种群结构对谱系树的整体影响。特别地,我们希望了解相较于单一随机交配(panmixic)种群的基础溯祖过程,种群结构是否会改变谱系树高度的平均值和方差。我们将再次利用指数分布的特性来近似事件发生时间(见第3.6节)。
让我们从”盒中虫”隐喻的角度来理解多个同类群间存在基因流时的溯祖过程,该隐喻曾用于描述基础溯祖过程。在种群分组的情况下,虫群分布在多个盒子中,每个盒子代表一个同类群。虫在盒内随机移动并相互吞噬以减少数量。同时存在迁移的可能性:随机选择一只虫并移至其他盒子。若迁移事件极少发生,则单个盒子在迁出或迁入虫之前就有较大机会被缩减至仅剩一只虫。此时需要经过长时间积累足够多的迁移事件,才能使整个盒群最终缩减至单只虫。当迁移事件频繁时,虫在盒间频繁移动,盒子间形成有效连接。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/b17846b64548966397eef5f8e59eccdc4f732b3701c781b8c166f15559273961.jpg
图 4.23 两个deme的假设系谱。初始时,每个deme中各存在三个谱系。回溯时间的第一个事件是某个谱系从deme 1迁移到deme 2。迁移发生后,deme 2中由于谱系数量增加导致溯祖概率上升,而deme 1中由于谱系减少导致溯祖概率下降。继续回溯时间,deme 1中发生一次溯祖事件,随后deme 2中也发生一次溯祖事件。先前迁出deme 1的谱系又随机迁回deme 1。只有当最后的两个谱系通过迁移进入同一个deme后,所有谱系才能溯至最近的共同祖先。
因此,当所有”盒子中的bug”通过吞噬最终变为单个bug时,等待迁移事件发生的时间应该极少或为零。
结合溯祖和迁移事件
通过增加另一种可能发生的事件类型(从当前时间回溯至所有谱系找到最近共同祖先的过程中),可以描述存在基因流的系谱。我们假设溯祖和迁移事件都是稀有事件(或<math display="inline">N_{e}</math>很大且迁移率很小),因此在时间回溯中发生的事件只能是溯祖或迁移。换句话说,我们假设迁移和溯祖事件是互斥的。这种互斥性假设至关重要。当两个独立过程同时运作时,溯祖模型就转化为追踪谱系回溯并等待事件发生的模式。当事件独立但互斥时,所有可能事件的概率会被相加以获得总事件发生概率。例如:在随机交配下,双等位基因位点的二倍体基因型为杂合体的概率是<math display="inline">2pq</math>。这是独立采样Aa和aA两种情况的概率之和(杂合体的概率并非<math display="inline">\left(pq\right)^{2}</math>,后者是同时采样Aa和aA的概率)。因此,如果我们能找到谱系每代迁移到不同deme的概率的指数近似,就可以将其直接叠加到溯祖概率的指数近似上。
在细分种群中,每个世代都可能发生谱系从一个deme迁移到其他deme的情况。迁移率<math display="inline">m</math>表示谱系每代迁移的概率。因此,谱系未迁移的概率为每代<math display="inline">1-m</math>。在经历<math display="inline">t</math>代后发生迁移事件的概率即为<math display="inline">t-1</math>代未迁移后发生迁移的概率乘积:
<math display="block">
P\big(T_{迁移}=t\big)=(1-m)^{t-1}m
</math>
这与第3章中给出的经过t代后发生溯祖(coalescent)事件的概率形式完全相同。与溯祖概率类似,随时间迁移的概率也是一个几何级数,可以用指数分布近似(见数学框3.2)。为了得到<math display="inline">e</math>的指数(或迁移过程的强度),我们需要确定种群中迁移发生的预期速率。
现在考虑基因流岛屿模型中的迁移事件,该模型包含<math display="inline">d</math>个繁殖群(deme),每个繁殖群包含<math display="inline">2N_{e}</math>个谱系。总种群大小为所有繁殖群大小之和,即<math display="inline">2N_{e}d</math>个谱系。当时间以连续尺度<math display="inline">t=\frac{j}{2N_{e}d}</math>度量时,一个时间单位相当于<math display="inline">2N_{e}d</math>代。若经过<math display="inline">2N_{e}d</math>代且每代迁移概率为<math display="inline">m</math>,则在整个种群中一个连续时间单位内预期会发生<math display="inline">2N_{e}dm</math>次迁移事件。若定义<math display="inline">M=4N_{e}m</math>,则<math display="inline">M/2</math>等价于<math display="inline">2N_{e}m</math>,即单个繁殖群内谱系的迁移概率(每繁殖群迁移率)。各繁殖群的迁移概率相互独立,因此整个种群中迁移事件的预期次数为各繁殖群迁移概率之和,即<math display="inline">\textstyle{\frac{M}{2}}d</math>。由此可得任一繁殖群中单个谱系在第<math display="inline">t</math>代迁移的指数近似概率:
<math display="block">
P\big(T_{migration}=t\big)=e^{-t\frac{M d}{2}}
</math>
在连续时间尺度上。当存在多个谱系时,每个谱系具有独立的迁移概率,但仅有一个谱系会发生迁移。因此,我们将所有<math display="inline">k</math>个谱系的<math display="inline">e^{-t_{2}^{M d}}</math>迁移概率相加,得到总迁移概率:
<math display="block">
P\big(T_{migration}=t\big)=e^{-t\frac{M d}{2}k}
</math>
适用于<math display="inline">d</math>个繁殖群的<math display="inline">k</math>个祖先谱系。<math display="inline">k</math>个谱系在某时刻或之前发生迁移的概率可通过累积指数分布近似:
<math display="block">
P\big(T_{migration}\leq t\big)=1-e^{-t\frac{M d}{2}k}
</math>
其推导方式与溯祖事件时间的近似方法完全相同。
当两个独立过程同时作用时,谱系回溯的系谱模型将转化为等待事件发生的模型。此时可能的事件为迁移或溯祖,因此任何事件的总概率为这两类互斥事件独立概率之和。由于谱系必须处于同一繁殖群才能溯祖,溯祖事件的概率为:
<math display="block">
P(T_{coal}\leq t)=1-e^{-t d\sum_{i=1}^{d}\frac{k_{i}(k_{i}-1)}{2}}
</math>
当第<math display="inline">i</math>个繁殖群有<math display="inline">k_{i}</math>个祖先谱系时,这是基本溯祖模型的改进版本,考虑了<math display="inline">d</math>个繁殖群和以<math display="inline">2N_{e}d</math>为尺度的时间。(注意当<math display="inline">d=1</math>时,连续时间尺度上的溯祖预期时间退化为<math display="inline">\frac{k(k-1)}{2}</math>。)回溯时间(增加<math display="inline">t</math>)时发生任一事件(溯祖或迁移)的总概率为:
<math display="block">
P(T_{event}\leq t)=1-e^{-t\left[d k_{2}^{M}+d\sum_{i=1}^{d}\frac{k_{i}(k_{i}-1)}{2}\right]}
</math>
其中指数项为迁移和溯祖过程强度的总和。在最简单的
当有两个繁殖群(<math display="inline">d=2</math>),每个繁殖群中分别有<math display="inline">k_{1}</math>和<math display="inline">k_{2}</math>条祖先谱系时,式4.86可简化为
<math display="block">
P(T_{e v e n t}\leq t)=1-e^{-t\left[(k_{1}+k_{2})\frac{M}{2}+\frac{k_{1}(k_{1}-1)}{2}+\frac{k_{2}(k_{2}-1)}{2}\right]}
</math>
(Hudson 1990中的示例),其中时间以总群体大小<math display="inline">2N_{e}d</math>或所有繁殖群中谱系数量之和为单位进行缩放。
当根据式4.86的指数分布在时间<math display="inline">t</math>发生事件时,需要判断该事件是合并还是迁移。事件为迁移或合并的总概率为<math display="inline">d k{\frac{M}{2}}+d\sum_{i=1}^{d}{\frac{k_{i}{\big(}k_{i}-1{\big)}}{2}}</math>。因此,事件为迁移的概率为
<math display="block">
\frac{d k\frac{\frac{M}{2}}{\displaystyle d k\frac{M}{2}+d\sum_{i=1}^{d}\frac{k_{i}(k_{i}-1)}{2}}}{d k\frac{M}{2}+d\sum_{i=1}^{d}\frac{k_{i}(k_{i}-1)}{2}}=\frac{k M}{k(M-1)+\sum_{i=1}^{d}k_{i}^{2}}
</math>
而事件为合并的概率为
<math display="block">
\frac{d\displaystyle\sum_{i=1}^{d}\frac{k(k_{i}-1)}{2}}{d k\displaystyle\frac{M}{2}+d\displaystyle\sum_{i=1}^{d}\frac{k_{i}(k_{i}-1)}{2}}=\frac{\displaystyle\sum_{i=1}^{d}(k_{i}^{2}-k_{i})}{k(M-1)+\displaystyle\sum_{i=1}^{d}k_{i}^{2}}
</math>
当发生合并事件时,由于具有更多祖先谱系的繁殖群更可能发生合并(繁殖群<math display="inline">j</math>发生合并的概率为<math display="inline">{\frac{\frac{k{\big(}k_{j}-1{\big)}}{2}}{\displaystyle\sum_{i=1}^{d}{\frac{k_{i}(k_{i}-1)}{2}}}}={\frac{k_{j}{\big(}k_{j}-1{\big)}}{\displaystyle\sum_{i=1}^{d}k_{i}(k_{i}-1)}}</math>),需随机选择一个繁殖群。
图4.24展示了当迁移率相对较高或较低时,合并与迁移联合过程的两次实现。每个事件的等待时间由式4.86指定的指数分布确定。
交互框4.8 两繁殖群间迁移的基因谱系
包含繁殖群间迁移可能的溯祖谱系可通过累积指数分布确定事件等待时间来构建。确定等待时间后,使用事件概率判断该事件是迁移还是合并。若为合并事件,则随机选择一个繁殖群中的一对随机谱系进行合并,该繁殖群的祖先谱系数<math display="inline">(k_{i})</math>减1。若为迁移事件,则随机选择一条谱系移入随机繁殖群。构建谱系的具体步骤请参考交互框3.4(编号80×3.4)。
教材网站提供了Microsoft Excel电子表格模型的链接,用于计算两繁殖群间迁移溯祖谱系所需参数。(作为替代方案,亦提供可生成谱系等待时间的简单R脚本。)
基因树在迁移下的平均长度
在确定结构化种群中基因树聚合的平均时间之前,首先需要引入一些有用的符号来描述谱系在种群内部和之间的可能分布位置。我们可以定义一个列表(或行向量)来追踪谱系在所有种群间的分配方式:
<math display="block">
\boldsymbol{d}=\left(d_{1},d_{2},d_{3},...,d_{n}\right)
</math>
第二种观察聚合与迁移的方式是使用教材网页上链接的Hudson Animator模拟器。模拟器中有三个可设置的参数:n:设置当前时间两个种群中采样的谱系数量(或式4.86中的<math display="inline">k_{1}+k_{2}</math>),而M1:和M2:分别设置每个时间段种群1和种群2的预期迁移个体数(或式4.83和4.85中的<math display="inline">M</math>)。点击Recalc将计算新基因树的等待时间。动画过程可通过图下方的按钮控制。当指针悬停在树的圆圈上时,右下角会显示等待时间。点击左上方的Trees标签可查看种群结构如何影响基因树本身。
初始设置n为10,M1和M2均为低迁移率0.1。模拟10次独立基因树;每次记录迁移事件数(动画中的浅蓝色圆圈)及聚合至单一最近共同祖先(MRCA)的总等待时间。将M1和M2提高至高迁移率1.0,再次模拟10次独立树,记录迁移事件数和至MRCA的总等待时间。迁移率较低或较高时,基因树在平均上有何差异?
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/afc3d2683328fcf0be972e3d105f804ea29a4208ec75d62456f0dc4d08600694.jpg
图4.24 六个谱系最初均分于两个种群的基因树,迁移率低(A)和高(B)的情况。当迁移概率低时,种群内的聚合事件倾向于在发生任何迁移事件前使所有种群内仅剩单一谱系。随后需长时间等待直至迁移事件将两个种群合并至一处才能聚合。当
其中每个<math display="inline">d_{i}</math>表示包含i个谱系的deme数量,<math display="inline">n</math>是deme的总数。总谱系数即为包含i个谱系的deme数量与谱系数i的乘积对所有可能的每deme谱系数求和,即<math display="inline">\sum_{i\mathop{=}1}^{n}i d_{i}</math>。当从包含两个deme的总种群中抽取两个谱系时,存在两种可能的采样方式:两个谱系可能从不同的deme中被采样得到<math display="inline">d=(2,0)</math>,或从单个deme中被采样得到<math display="inline">d=(0,1)</math>。这种符号系统定义了从若干deme中抽取一定数量谱系时所形成的样本配置。图4.25展示了两个或三个deme中两到三个谱系的样本配置示例。当谱系合并为单个祖先谱系时,样本配置变为(1)。这种样本配置符号非常有用,因为结构化种群中合并时间的均值与方差取决于谱系是否位于同一deme。
在掌握样本配置的基本概念后,我们将推导结构化种群中合并时间的平均值和谱系树总长度的期望值。我们将重点关注两个deme中最简单的两谱系情形。需要确定两种可能的样本配置((2,0)或(0,1))中任一配置下两个谱系发生合并的概率。图4.26展示了这些样本配置状态之间可能的转移过程。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/ed733b8a89d3d2d8d12c88d39fa58241138007f52c2e63e6a3fc00a4c2f13811.jpg
图4.25 两个谱系和两个deme的样本配置(A)以及三个谱系和三个deme的样本配置(B)。谱系用圆点表示,deme之间的分隔用虚线表示。每个样本配置仅展示一种可能情形,尽管某些配置可能存在多种实现方式。例如,(0,1)可以出现在两个谱系均位于左侧deme或均位于右侧deme时。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/587a33cd605d289e5afde557779381e34ccd6c6135bc7952490cf14292002617.jpg
图4.26 当两个谱系位于同一deme(0,1)或不同deme(2,0)时可能发生的事件及其对应概率。deme之间的分隔用虚线表示。仅当谱系位于同一deme时才能发生合并。合并概率(A)、单个谱系迁移使两谱系分处不同deme(B)、以及迁移使两谱系共处同一deme(C)共同决定两个谱系发生合并的总体概率。两个谱系同时迁移的概率(<math display="inline">m^{2}</math>)未在B中展示,该情形适用于存在三个及以上deme的情况。
与基础溯祖过程类似,溯祖概率是种群大小的倒数与可能发生溯祖的独特谱系对数量的乘积。若每个deme包含<math display="inline">2N_{e}</math>个谱系,则同一deme中两个谱系的溯祖概率为<math display="inline">\frac{1}{2N_{e}}</math>。然而,两个谱系必须处于同一deme才可能溯祖,而受限的基因流会降低这种可能性。
对于处于同一deme或样本配置(0,1)的两个谱系,最终导致溯祖的可能事件有两种。第一种可能是两个谱系直接以概率<math display="inline">\displaystyle\frac{1}{2N_{e}}</math>溯祖。第二种可能是一个或两个谱系在溯祖前迁移到其他deme。若每个deme每代迁移比例为<math display="inline">m</math>,则单个谱系迁出的概率为<math display="inline">m</math>,未迁出的概率为<math display="inline">1-m</math>。一个谱系迁移而另一个未迁移的概率为<math display="inline">m(1</math><math display="inline">-m)+(1-m)m=2m(1-m)</math>。两个谱系同时迁移的概率为<math display="inline">m^{2}</math>。因此,至少一个谱系迁移的总概率为<math display="inline">2m(1-m)+m^{2}</math>,当<math display="inline">m</math>较小时可近似为<math display="inline">2m</math>(忽略<math display="inline">m^{2}</math>项)。对于同一deme或(0,1)配置的两个谱系,前一代发生任一事件(溯祖或迁移)的总概率为<math display="inline">2m+\frac{1}{2N_{e}}</math>。
对于不同deme或样本配置(2,0)的两个谱系,根据与单deme情况相同的逻辑,一个谱系迁移的总概率为<math display="inline">2m</math>。然而,从(2,0)转变为(0,1)时,迁移必须进入第二个谱系所在的特定deme。迁移到特定deme的概率为<math display="inline">\frac{1}{d-1}</math>,其中<math display="inline">d</math>为deme总数。因此,初始分离的两个谱系最终进入同一deme的总概率为<math display="inline">\frac{2m}{d-1}</math>。
为确定两个deme中的平均溯祖时间,可利用指数分布过程中事件平均时间为事件概率倒数的性质。设<math display="inline">\overline模板:T_{(0,1)}</math>表示同deme两谱系的平均溯祖时间,<math display="inline">\overline模板:T_{(2,0)}</math>表示异deme两谱系的平均溯祖时间。对于同deme两谱系,其平均溯祖时间等于立即溯祖的平均时间加上迁移后处于异deme状态的时间期望。发生任一事件(溯祖或迁移)的平均时间为事件总概率的倒数,即<math display="inline">\frac{1}{2m+\displaystyle\frac{1}{2N_{e}}}</math>。当事件发生时,有<math display="inline">\frac{1}{2N_{e}}</math>概率为溯祖,<math display="inline">2m</math>概率为迁移。综合这些因素可得同deme两谱系的平均溯祖时间表达式:
<math display="block">
\overline模板:T_{(0,1)}=\frac{\displaystyle\frac{1}{2N_{e}}}{\displaystyle2m+\frac{1}{2N_{e}}}+\frac{\displaystyle2m}{\displaystyle2m+\frac{1}{2N_{e}}}\overline模板:T_{(2,0)}
</math>
对于两个不同繁殖群(deme)中的谱系,其平均合并时间是迁移至同一繁殖群所需的平均时间与一旦谱系处于同一繁殖群后的平均合并时间之和。由于迁移至同一繁殖群的几率为 <math display="inline">2m{\frac{1}{d-1}}</math> ,两个谱系迁移至同一繁殖群的平均时间为 <math display="inline">\frac{d-1}{2m}</math> 。因此,两个不同繁殖群中谱系的平均合并时间为
<math display="block">
\overline模板:T_{(2,0)}=\frac{d-1}{2m}+\overline模板:T_{(0,1)}
</math>
通过解这两个方程(见数学框4.2),可得
<math display="block">
\overline模板:T_{(0,1)}=2N_{e}d
</math>
及
<math display="block">
\overline模板:T_{(2,0)}=2N_{e}d+\frac{d-1}{2m}
</math>
(见 Slatkin 1987b;Strobeck 1987;Nordborg 1997;Wakeley 1998)。
这两个繁殖群情境下两个谱系的平均合并时间均为简洁表达式,易于解释。方程4.93略显意外,因为它表明同一繁殖群中两个谱系的平均合并时间与迁移率无关,而仅取决于总群体大小,如同随机交配群体(注意若每个繁殖群包含 <math display="inline">2N_{e}</math> 个谱系,则总群体大小为 <math display="inline">N_{T}=2N_{e}d</math>)。通过想象迁移率变化时的情形,我们可以理解这一结果。若迁移率降低,谱系迁移至其他繁殖群的几率减小,从而缩短合并时间。然而,当迁移事件确实发生时,谱系需更长时间才能迁移回原繁殖群并合并。由于这两种效应随迁移率变化精确抵消,平均合并时间与迁移率无关。当两个谱系位于不同繁殖群时,平均合并时间随迁移率降低或繁殖群数量增加而延长。平均合并时间与迁移率成反比,因为需通过随机迁移才能使两个谱系进入同一繁殖群。随着繁殖群数量增加,两个谱系分隔的可能性增大,因此需要更多迁移事件才能使它们处于同一繁殖群。
繁殖群内与总群体中的平均合并时间也可用于表征群体结构程度。本章前文曾通过自合子性(autozygosity)概率,以总群体中随机抽取的两个等位基因状态不同的几率 <math display="inline">(H_{T})</math> 与亚群体中随机抽取的两个等位基因状态不同的几率 <math display="inline">(H_{S})</math> 之差(或 <math display="inline">F_{S T}=\frac{H_{T}-H_{S}}{H_{T}}</math>)描述群体结构。对于从 <math display="inline">d</math> 个繁殖群构成的总群体中随机抽取的两个谱系,有 <math display="inline">\frac{1}{d}</math> 的概率来自同一繁殖群,<math display="inline">\frac{d-1}{d}</math> 的概率来自不同繁殖群。因此,从结构化群体中随机抽取的两个谱系的平均合并时间为
<math display="block">
\overline{{{T}}}=\frac{1}{d}\overline{{{T}}}_{(0,1)}+\frac{d-1}{d}\overline{{{T}}}_{(2,0)}=2N_{e}d+\frac{(d-1)^{2}}{2m d}
</math>
and Eq. 4.93 提供了从同一繁殖群中取样的两个谱系的平均溯祖时间<math display="inline">(\overline模板:T_{(0,1)}=2N_{e}d,</math> )。将这两个平均溯祖时间结合
<math display="block">
F_{S T}=\frac{\overline模板:T-\overline模板:T_{(0,1)}}{\overline模板:T}
</math>
可得到从溯祖时间视角解释种群结构的表达式(Slatkin 1991)。于是种群结构可被
Math box 4.4 Solving two equations with two unknowns for average coalescence times
我们将式4.91和4.92重新表述为
<math display="block">
\begin{array}{l}{{\displaystyle T_{(0,1)}=x=a+b y}}\ {{}}\ {{\displaystyle\overline模板:\cal T_{(2,0)}=y=c+x}}\end{array}
</math>
<math display="block">
\gamma=\frac{\displaystyle\frac{d-1}{2m}+\frac{1}{f}}{\displaystyle\frac{1}{2N_{e}}}
</math>
当分子分母同乘f时得到
<math display="block">
\gamma=\frac{f\frac{d-1}{2m}+1}{\frac{1}{2N_{e}}}
</math>
<math display="inline">c=\frac{d-1}{2m}</math> 当时间以<math display="inline">2N_{e},</math>为单位标度化时,<math display="inline">a=\frac{1}{2m+\displaystyle\frac{1}{2N_{e}}}.</math>
将<math display="inline">\boldsymbol{X}</math>的方程代入y的方程可得
<math display="block">
\gamma=c+a+b\gamma
</math>
将<math display="inline">f</math>的完整表达式代入并展开后得到
经整理得
<math display="block">
y={\frac{\displaystyle\left(2m+{\frac{1}{2N_{e}}}\right){\frac{d-1}{2m}}+1}{\displaystyle={\frac{1}{2N_{e}}}\left({\frac{2N_{e}2m(d-1)+(d-1)+2N_{e}2m}{2m}}\right)}}
</math>
<math display="block">
y-b y=c+a
</math>
进而
<math display="block">
\gamma={\frac{c+a}{1-b}}
</math>
将<math display="inline">a,b,</math>和<math display="inline">c</math>的值代入后得到
用乘以<math display="inline">2N_{e}</math>代替除以<math display="inline">\frac{1}{2N_{e}}</math>可消去分子中的<math display="inline">\frac{1}{2N_{e}}</math>项,展开后得到
<math display="block">
\gamma={\cfrac{{\cfrac{d-1}{2m}}+{\cfrac{1}{2m+{\cfrac{1}{2N_{e}}}}}}{1-\left({\cfrac{2m}{2m+{\cfrac{1}{N_{e}}}}}\right)}}
</math>
<math display="block">
\gamma=\frac{2N_{e}2m d}{2m}-\frac{2N_{e}2m}{2m}+\frac{d-1}{2m}+\frac{2N_{e}2m}{2m}
</math>
经合并同类项后最终得到
上述分母可重新整理为<math display="inline">{\frac{2m+{\frac{1}{N e}}}{2m+{\frac{1}{N e}}}}-{\frac{2m}{2m+{\frac{1}{N e}}}}={\frac{\frac{1}{2N e}}{2m+{\frac{1}{2N e}}}}</math>。令f = 2m + 1并代入整理后的分母方程得
<math display="block">
\gamma=2N_{e}d+\frac{d-1}{2m}
</math>
将<math display="inline">\gamma</math>的表达式代入后,<math display="inline">\overline模板:T_{(2,0)}</math>的方程可通过类似代数方法求解。
理解为从整体种群中取样的一对谱系与从亚种群内取样的一对谱系在平均溯祖时间上的差异。
一般而言,种群细分会延长谱系溯至最近共同祖先所需的时间。当基因流相对受限时,繁殖群内的共祖过程与孤立随机交配群体中的过程相似。然而,每个繁殖群的单一祖先需要等待相对稀有的迁移事件,才能使不同繁殖群的两个谱系共祖。这往往会产生具有长分支的系统树,连接不同繁殖群的祖先个体。随着迁移率增加,系统树分支长度逐渐趋近于与总规模相同的单一随机交配群体中的模式,因为迁移事件频繁地将谱系在繁殖群间转移。
第4章 复习
个体与亚种群在空间和时间上的分离导致种群内交配的非随机性。若无足够的基因流维持随机交配(panmixia),遗传漂变将导致亚种群间等位基因频率的分化。
距离隔离是一个普适性预测,因为随着亚种群空间分离的增加,基因流预期会减少。
多种基因流模型(如岛屿模型或踏脚石模型)描述了多个亚种群间的遗传混合模式。
大陆-岛屿模型和双岛模型表明,随时间推移,基因流会使等位基因频率均质化至平衡值,该值取决于亚种群间基因流速率的模式。
基因流水平可通过直接追踪当代种群中的亲缘关系(直接估计)来测量。亲缘分析利用子代基因型和一个已知亲本推断未知亲本的单体型。随后,该未知亲本单体型被用于从候选亲本池中排除不可能的父母个体。此方法鉴定真实亲本的能力取决于特定单体型在种群中随机出现的概率。
区分群体内与群体间的溯祖事件,可推导出细分种群中基因谱系可分为两个时间尺度的普遍结论。一个时间尺度是各群体近期发生群体内溯祖事件和迁移事件的谱系历史;另一时间尺度是总种群中祖先谱系更久远的历史。Wakeley(1998, 1999)将近期时间尺度描述为细分种群谱系的散射阶段(scattering phase),更深层时间尺度称为收集阶段(collecting phase)。时间尺度的分离现象也在具有灭绝-再定殖机制的细分种群(Wakeley和Aliacar 2001)以及存在距离隔离的连续种群(Wilkins 2004)中被研究。
关键洞见在于:特定条件下,多态性模式主要源于收集阶段的谱系分选,而对发生迁移事件的散射阶段依赖较小。收集阶段的谱系部分可由标准溯祖过程描述,其时间尺度通过恰当的Ne标定且不受迁移影响。其结果是,可能无法判定遗传多态性的不同模式究竟源于群体规模差异、群体数量差异、群体间有效迁移率差异,还是总种群增长等历史事件,因为这些变量对整体谱系具有可互换的影响效应。
<math display="inline">F_{I S}</math> 衡量杂合基因型与随机交配相比的平均过剩或缺失。<math display="inline">F_{S T}</math> 衡量由于种群结构导致的亚种群杂合性缺失,相对于随机交配群体预期杂合性的差异。<math display="inline">F_{I T}</math> 衡量由亚种群内非随机交配和等位基因频率分化共同导致的杂合基因型总体过剩或缺失。众多理想化<math display="inline">F_{S T}</math>的估计量(如<math display="inline">G_{S T}</math>)考虑了实际遗传数据的细节:一个位点存在两个以上等位基因、多个位点的平均效应、有限且可能不等的样本量。
Wahlund效应表明,遗传变异可以储存为亚种群间等位基因频率的方差,或随机交配种群内的杂合性。分化亚种群的融合或随机交配种群的分割,可将一种类型的遗传变异转化为另一种类型。
通过比较一组亚种群间遗传分化的程度和模式与基因流和遗传漂变模型的预测值,可间接估计基因流速率。例如,在无限岛屿模型下,平衡状态<math display="inline">F_{S T}</math>近似等于有效迁移率四倍加一的倒数<math display="inline">(\frac{1}{4N_{e}m+1})</math>。在二维距离隔离模型中,线性化<math display="inline">\hat{F}_{S T}</math>预期会随地理距离的对数增加而增加。集合种群模型包括配子和个体在亚种群间的迁移、亚种群的灭绝与重建。空间显式方法利用景观特征建模基因流的最小成本路径,或通过电路理论建模连接亚种群的多路径网络及其可变基因流速率。
多基因座基因型可通过最大似然法或贝叶斯后验概率将个体分配到起源亚种群。贝叶斯方法可扩展用于确定最优支持的亚种群数量,以及每个个体多基因座基因型中各亚群来源的比例。主成分分析(PCA)可降低含多等位基因位点的大规模遗传数据维度,用于识别遗传亚群及具有多亚群近期祖先的个体。
分割种群中的谱系树可用指数分布等待时间建模,其中迁移概率与溯祖概率相结合。在两个deme中,同一deme内两个谱系的平均溯祖时间等于总种群大小且与迁移率无关。不同deme中的两个谱系,其平均溯祖时间随deme数量增加和迁移率降低而延长,因为仅当两个谱系处于同一deme时才能溯祖。与同亚种群采样的两个谱系相比,从整个种群随机采样的两个谱系的平均溯祖时间因种群结构和有限基因流而延长。
Further reading
章末习题
1 在犯罪调查中,从犯罪现场获取的多位点DNA图谱作为证据时,可与数据库记录中数百万份多位点DNA图谱进行比对。请解释为何这种做法可能导致证据DNA样本遗留者的多位点DNA图谱与数据库中另一不同个体的DNA图谱产生高概率的随机匹配。
2 使用文本模拟网站Simulations <math display="inline">_-></math> Fixation Indices完成本题。模拟对话框包含各局域种群的有效种群大小(<math display="inline">N_{e}</math>)、迁移率,以及双等位基因位点在每个局域种群的初始等位基因频率。保持总种群数和共祖系数为默认值。运行下表中参数组合的模拟,并在空白处记录结果。每组合至少运行两次模拟,以了解相同参数下结果的变异程度。记录各<math display="inline">F</math>指数首次达到近似最大值时的世代数。为便于比较,将所有条件组的模拟时间尺度统一设置为500世代以内。
本题亦可使用Populus软件完成(从主菜单选择Mendelian Genetics,再选择Population Structure;将局域种群数设为10)。
关于景观遗传学中种群内与种群间遗传变异空间格局的预测方法与估计量的综述,参见:
Balkenhol, N., Cushman, S.A., Storfer, A.T., and Waits, L.P. (eds.) (2015). Landscape Genetics. Chichester, UK: Wiley.
欲了解植物Linanthus parryae在距离隔离理论发展中的作用,以及蓝白花色空间分布不同解释背后的人物轶事,参见:
Provine, W.B. (1986). Sewall Wright and Evolutionary Biology. Chicago, IL: University of Chicago Press.
关于基因组时代的亲本分析展望,参见:
Flanagan, S.P. and Jones, A.G. (2018). The future of parentage analysis: from microsatellites to SNPs and beyond. Molecular Ecology 28: 544–567.
种群结构概念与实证估计、基因流间接估计的综述参见:
Holsinger, K.E. and Weir, B.S. (2009). Genetics in geographically structured populations: defining, estimating and interpreting Fsr. Nature Reviews Genetics 10: 639–650.
多倍体物种杂合度与种群分化估计方法的概述参见:
Meirmans, P.G., Liu, S., and van Tienderen, P.H. (2018). The analysis of polyploid genetic data. Journal of Heredity 109: 283–296.
关于贝叶斯统计方法在遗传学中的应用及其如何推动群体遗传学与基因组学假设检验新途径的综述,参见:
Beaumont, M.A. and Rannala, B. (2004). The Bayesian revolution in genetics. Nature Reviews Genetics 5: 251–261.
溯祖模型背景下种群结构影响的综述参见:
Charlesworth, B., Charlesworth, D., and Barton, N.H. (2003). The effects of genetic and geographic structure on neutral variation. Annual Review of Ecology and Systematics 34: 99–125.
<table>
<tr>
<th>Deme size (Ne)</th>
<th>m</th>
<th>Initial freq(A)</th>
<th>F<sub>IS</sub></th>
<th>F<sub>ST</sub></th>
<th>F<sub>IT</sub></th>
</tr>
<tr>
<td>10<br>10</td>
<td>0<br>0.001</td>
<td>0.5<br>0.5</td>
<td></td>
<td></td>
<td></td>
</tr>
<tr>
<td>10</td>
<td>0.1</td>
<td>0.5</td>
<td></td>
<td></td>
<td></td>
</tr>
<tr>
<td>10</td>
<td>0.1</td>
<td>0.8</td>
<td></td>
<td></td>
<td></td>
</tr>
<tr>
<td>50</td>
<td>0</td>
<td>0.5</td>
<td></td>
<td></td>
<td></td>
</tr>
<tr>
<td>50</td>
<td>0.001</td>
<td>0.5</td>
<td></td>
<td></td>
<td></td>
</tr>
<tr>
<td>50</td>
<td>0.1</td>
<td>0.5</td>
<td></td>
<td></td>
<td></td>
</tr>
<tr>
<td>100</td>
<td>0</td>
<td>0.5</td>
<td></td>
<td></td>
<td></td>
</tr>
<tr>
<td>100</td>
<td>0.001</td>
<td>0.5</td>
<td></td>
<td></td>
<td></td>
</tr>
<tr>
<td>100</td>
<td>0.1</td>
<td>0.5</td>
<td></td>
<td></td>
<td></td>
</tr>
</table>
从生物学和数学上定义 $H_{I}$、$H_{S}$ 和 $H_{T}$。用数学表达式(使用 $H$ 符号)和生物学意义定义 $F_{IS}$、$F_{ST}$ 和 $F_{IT}$。
在模拟中,等位基因频率线有时会触及顶部或底部坐标轴(达到固定或丢失)后重新出现。这些情况发生了什么?你在模拟中设置的迁移值单位是什么(例如 0.001 或 0.1)?该值的增加在生物学上意味着什么?为什么增加 $m$ 会维持较低的 $F_{ST}$ 和 $F_{IT}$ 值?迁移如何抵消遗传漂变?迁移是否总能强到实现这一点?用模拟观察结果解释。
3 使用文本模拟网站 Simulations → Fixation Indices 解决此问题。什么是共祖系数($f$)?对 $N_e=20$ 和 $m=0.01$,运行 $f$ 值为 $-0.5$、$0.0$ 和 $0.5$ 的模拟 100 代。用下表记录第 100 代观察到的值。
| 共祖系数(f)
|
H
|
Hs
|
H
|
Fis
|
FsT
|
FT
|
| -0.5
|
|
|
|
|
|
|
| 0.0
|
|
|
|
|
|
|
| 0.5
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
对于相同的<math display="inline">f\ell</math>值,<math display="inline">H_{I}</math>和<math display="inline">H_{S}</math>如何比较?<math display="inline">F_{I S}</math>和<math display="inline">F_{S T}</math>如何随<math display="inline">f\zeta</math>变化?为什么?
4 1965年,Sick(Hereditas 54 : 49–69)对鳕鱼(codfish)的血红蛋白基因进行了同工酶多态性测量。他的目标是记录鳕鱼的迁徙和交配模式以用于资源管理,并鉴定繁殖种群。他在三个地理区域各1000尾鱼的样本中观察到的基因型如下表所示(F代表快,S代表慢——各等位基因在淀粉凝胶中的迁移速率)。地理采样区域标注于地图(来自https://www.google.com/maps/place/Baltic+Sea)。请根据观察到的等位基因和基因型频率,用定量推理回答每个问题。
文件:Https://cdn-mineru.openxlab.org.cn/extract/25170dbb-f7fa-43db-aad1-b5684c7fb850/6f965d6cd623d51fe6a528d457ca6aeb43b4255585057da56cc3a02ee0d6abf7.jpg
|
|
Genotype
|
|
|
FF
|
| Area1
|
40
|
| Area2
|
640
|
| Area3
|
340
|
三个区域的观测等位基因频率是多少?根据基因型频率,你能推断各区域内鳕鱼的交配模式吗?区域1和2是否完全存在自由基因流动?区域1和2的鱼群能否作为单一种群管理?哪些基因流动和种群结构过程可以解释区域3内观察到的等位基因和基因型频率?
5 两个亚种群在一个具有四个等位基因的位点上拥有非重叠等位基因。亚种群1的等位基因频率为<math display="inline">p_{1}=p_{2}=0.5</math>且<math display="inline">p_{3}=p_{4}=0</math>,而亚种群2的等位基因频率为<math display="inline">p_{1}=p_{2}=0</math>且<math display="inline">p_{3}=p_{4}=0.5</math>。计算<math display="inline">H_{S}</math>和<math display="inline">H_{T}</math>,并用其计算<math display="inline">G_{S T}</math>和Jost’s <math display="inline">D</math>。每个指数捕捉了种群间遗传变异的哪些模式?为什么它们会不同?
6 个人基因分型服务提供客户祖先来源种群的信息。这些服务依赖哪些类型的位点?它们使用什么模型来估算祖先生活过的世界区域?
7 在Math Box 4.2中,设电阻值为<math display="inline">\mathrm{R}1=\mathrm{R}3=1</math>,<math display="inline">\mathrm{R}4=\mathrm{R}5=4</math>,<math display="inline">\mathrm{R}2=4</math>。求解电压V1、V2和V3,再计算各节点的电流值。根据电流值,对亚种群A和B之间每条路径的基因流动量及节点3的死亡率给出生物学解释。
8 根据互动框4.7中的指导,为6个总谱系(初始划分为两个繁殖群<math display="inline">k_{1}=k_{2}=3</math>)构建一个溯祖谱系。使用<math display="inline">2N=50</math>和迁移率0.1(注意:该突变率设定过高以确保发生多次迁移事件。若迁移事件过多可调整迁移率)。使用坐标纸并在谱系图上绘制连续时间和离散时间标尺以标注突变与合并事件。重复模拟以观察基于相同漂变和迁移率的重复杂谱系差异。作为对比,模拟并绘制迁移率为0.01的谱系。根据观测的等待时间解释模拟谱系中<math display="inline">F_{ST}</math>的含义。
9 在文献中检索近期使用本章所述群体遗传预测的研究论文。主题可为任何生物体、应用或过程,但论文必须包含涉及群体间遗传分化、<math display="inline">F_{ST}</math>或其估计量、有效迁移率<math display="inline">\left(N_{e}m\right)</math>或基因流模式的假设检验。总结论文的主要假设、目标或理论基础,解释论文如何运用本章的群体遗传预测,并归纳基于该预测的研究结果与结论。
10 构建两个经历基因流和遗传漂变的亚群体间遗传分化的模拟模型。电子表格模型的搭建指南可在教材网站找到。该指南也可用于Python或R等编程语言的实现。
问题框4.1答案
通过表4.3获得父本单体型中各等位基因的频率。对于树4865,每个基因座仅有一个可能的父本等位基因。任一基因型在每个基因座上携带一个父本等位基因拷贝的概率为:
A: <math display="inline">(0.1216)^{2}+2(0.1216)(1-0.1216)=0.2284</math>
B: <math display="inline">(0.3971)^{2}+2(0.3971)(1-0.3971)=0.6365</math>
C: <math display="inline">(0.0761)^{2}+2(0.0761)(1-0.0761)=0.1464</math>
D: <math display="inline">(0.1905)^{2}+2(0.1905)(1-0.1905)=0.3447</math>
E: <math display="inline">(0.1250)^{2}+2(0.1250)(1-0.1250)=0.2344</math>
单个基因座上,父本等位基因预计出现在14%至64%的可能基因型中。五个基因座全部随机匹配的概率为<math display="inline">0.2284\times0.6365\times0.1464\times0.3447\times0.2344=0.0017</math>,即每10 000个随机基因型中出现17次。排除概率为<math display="inline">1-0.0017=0.9983</math>,而30个候选亲本的样本排除概率为<math display="inline">(0.9983)^{30}=0.9\dot{5}02</math>。约有95%的概率在30个候选亲本中不会出现随机匹配,因此我们高度确信4865号树是989号树种子25-1的真实父本。对于该子代-母本组合,B基因座在亲权鉴定中最不具分辨力,因为106等位基因频率接近40%。C基因座的167等位基因(频率略超7%)最具分辨力。
观测到的平均杂合子频率为0.22或22%。
<math display="inline">H_{S}=\frac{1}{n}\sum_{i=1}^{n}2p_{i}q_{i}</math>,其中<math display="inline">p_{i}</math>和<math display="inline">q_{i}</math>为亚群体<math display="inline">i</math>中的等位基因频率。
$$
<math display="inline">H_{T}=2\overline{p}\overline{q}</math>,其中<math display="inline">\bar{p}</math>和<math display="inline">\overline{q}</math>是所有亚群的平均等位基因频率。令<math display="inline">f</math>为快速等位基因的频率,<math display="inline">s</math>为慢速等位基因的频率,满足<math display="inline">f+s=1</math>。接着,估算总种群中快速等位基因的平均频率(慢速等位基因的频率可通过减法得出):
<math display="block">
\begin{array}{c}{\overline{f}=(0.0+0.93+0.17+0.51)/4}\ {\overline{f}=0.4025}\end{array}
</math>
而另一等位基因的频率为<math display="inline">{\overline{s}}=1-0.4025=0.5975</math>。
<math display="block">
\begin{array}{c}{{H_{T}=2(0.4025)(0.5975)}}\ {{{}}}\ {{H_{T}=0.481}}\end{array}
</math>
现可用<math display="inline">H_{I},H_{S},</math>和<math display="inline">H_{T}</math>计算<math display="inline">F</math>统计量。
<math display="block">
F_{I S}=\frac{H_{S}-H_{I}}{H_{S}}
</math>
问题框4.2解答
<math display="inline">H_{I}=\frac{1}{n}\sum_{i=1}^{n}\hat{H}_{i}</math>,其中<math display="inline">\hat{H}</math>是每个<math display="inline">n</math>个亚群中观测到的杂合子频率。
<math display="block">
\begin{array}{c}{{H_{I}=(0.0+0.14+0.34+0.40)/4}}\ {{{}}}\ {{H_{I}=0.22}}\end{array}
</math>
<math display="block">
\begin{array}{c}{F_{I S}=(0.228-0.220)/0.228}\ {F_{I S}=0.035}\end{array}
</math>
由于这四个种群的观测杂合度与随机交配下的预期值非常接近,未发现自交的证据。比较各群体的观测与预期杂合度可知,亚群9和43的杂合子略有超额,而亚群68存在约<math display="inline">10\%</math>的赤字。这三个偏差与亚群1的零偏差平均后总体接近0。
<math display="block">
F_{S T}={\frac{H_{T}-H_{S}}{H_{T}}}
</math>
<math display="block">
F_{S T}=(0.481-0.228)/0.481
</math>
<math display="block">
F_{S T}=0.526
</math>
亚群内的杂合度低于基于总种群等位基因频率的Hardy-Weinberg预期值。该值反映了亚群等位基因频率的显著差异。
<math display="block">
F_{I T}=\frac{H_{T}-H_{I}}{H_{T}}
</math>
<math display="block">
\begin{array}{c}{{F_{I T}=(0.481-0.220)/0.481}}\ {{{}}}\ {{F_{I T}=0.543}}\end{array}
</math>
这是由种群内非随机交配和亚群间等位基因频率分化共同导致的杂合度赤字。本例中,几乎所有杂合度赤字都源于亚群间的等位基因频率分化。
三个固定指数的关系为:
<math display="block">
\big(1-F_{I T}\big)=\big(1-F_{I S}\big)\big(1-F_{S T}\big)
</math>
用<math display="inline">\bar{F}_{I S}</math>和<math display="inline">\boldsymbol{F}_{S T}</math>的值求解<math display="inline">\bar{F}_{I T}</math>,可得与直接计算相同的数值:
问题框4.3解答
Wahlund效应表明,种群结构会导致杂合子频率降低、纯合子频率升高,其幅度与种群间等位基因频率分化的程度成正比。使用表2.3的等位基因频率,可通过式4.36(纯合位点)和式4.37(杂合位点)计算每个基因座经种群调整后的预期基因型频率:
D3S1358 <math display="inline">2(0.2118)(0.1626)(0.95)=0.0655</math>
D21S11 <math display="inline">2(0.1811)(0.2321)(0.95)=0.0799</math>
D18S51 <math display="inline">(0.0918)^{2}+(0.0918)(0.9082)(0.05)=0.0126</math>
vWA <math display="inline">(0.2628)^{2}+(0.2628)(0.7372)(0.05)=0.0788</math>
FGA <math display="inline">2(0.1378)(0.0689)(0.95)=0.0181</math>
D8S1179 <math display="inline">2(0.3393)(0.2015)(0.95)=0.1299</math>
D5S818 <math display="inline">2(0.3538)(0.1462)(0.95)=0.0942</math>
D13S317 <math display="inline">2(0.0765)(0.3087)(0.95)=0.0448</math>
D7S820 <math display="inline">2(0.2020)(0.1404)(0.95)=0.0539</math>
假设Amelogenin基因座不受种群结构影响,经种群结构调整后的10个基因座基因型期望频率为 <math display="inline">0.0655\times0.0799\times0.0126\times0.0788\times</math> <math display="inline">0.0181\times0.1299\times0.0942\times0.0448\times</math> <math display="inline">0.0539\times0.5=1.514\times10^{-12}</math>,其比值比为1/660 501 981 506。与随机交配【“panmixia”译为“随机交配”】假设下的基因型期望频率 <math display="inline">1.160\times10^{-12}</math>(比值比1/862 379 847 814)相比,考虑种群结构后该基因型偶然出现的可能性更高,但其期望频率仍极其罕见。
问题框4.4答案
<math display="block">
\begin{array}{c}{{(1-F_{I T})=(1-0.035)(1-0.526)}}\ {{{}}}\ {{(1-F_{I T})=(0.965)(0.474)}}\ {{{}}}\ {{(1-F_{I T})=0.4574}}\ {{{}}}\ {{F_{I T}=0.543}}\end{array}
</math>
基于全部43个亚种群的数据,Levin(1978)估算出P. cuspidata的 <math display="inline">F_{I S}=0.70</math>、<math display="inline">F_{S T}=0.80</math>和 <math display="inline">F_{I T}=0.80</math>。
遗传漂变与迁移在固定指数中的联合效应可表示为:
<math display="block">
F_{t}=\frac{1}{2N_{e}}\left(1-m\right)^{2}+\left(1-\frac{1}{2N_{e}}\right)F_{t-1}\left(1-m\right)^{2}
</math>
若用<math display="inline">X</math>表示自交合概率,<math display="inline">y</math>表示异交合概率(<math display="inline">\boldsymbol{y}=1-\boldsymbol{x}</math>),则可推广为:
<math display="block">
F_{S T}\approx{\frac{1}{N_{e}m+1}}
</math>
<math display="block">
F_{t}=x{\left(1-m\right)}^{2}+y F_{t-1}{\left(1-m\right)}^{2}
</math>
对于二倍体核基因座,取<math display="inline">\begin{array}{r}{X=\frac{1}{2N_{e}}}\end{array}</math>和<math display="inline">\begin{array}{r}{\gamma=1-\frac{1}{2N_{e}}}\end{array}</math>以获得平衡状态下<math display="inline">\boldsymbol{F}_{S T}</math>与<math display="inline">N_{e}m</math>的关系。Y染色体与细胞器基因座为单倍体且单亲遗传,其有效种群大小为核基因座的四分之一。例如人类线粒体基因组仅母系遗传(占种群半数),且为单倍体(拷贝数为核基因组半数)。对此类基因座,取<math display="inline">\begin{array}{r}{\chi=\frac{1}{\frac{N e}{2}}=\frac{2}{N e}}}\end{array}</math>和<math display="inline">\begin{array}{r}{y=1-\frac{2}{N_{e}}}\end{array}</math>,可得:
结果表明,Y染色体与细胞器基因座的<math display="inline">F_{S T}</math>预期更高(因其有效种群更小,见图4.15)。当所有类型基因座共享相同迁移率时,相较于二倍体核基因座,Y染色体与线粒体基因座的<math display="inline">\boldsymbol{F}_{S T}</math>水平高四倍。亚种群间Y染色体与细胞器基因座的分化程度更高,完全源于这些基因座自交合特性的差异导致遗传漂变引起的固定或丢失速率增加。详见Hu与Ennos(1999)及Hamilton与Miller(2002)。
