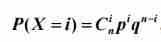生物统计漫谈:修订间差异
无编辑摘要 |
W. Machine(留言 | 贡献) 按个人理解写了,可能不是非常严谨;改了超多格式,但不知道手机版看上去怎么样;暂时没板子写不了公式;写不动了去睡觉 |
||
| 第1行: | 第1行: | ||
苯人数学不好,请大家帮忙指错并严厉批评(() | 苯人数学不好,请大家帮忙指错并严厉批评(() | ||
==概念== | |||
===总体·样本·理论=== | |||
具有相同性质的个体所组成的集合称为总体……从总体中抽出的若干个体所构成的集合称为样本。——《生物统计学(第5版)》李春喜等 | |||
总体分为有限总体(其中个体数量有限,如一个班级的所有人)和无限总体(个体数量极大或无限,如一棉田中棉铃虫的总数;其中无限总体可以更抽象地拓展为理论总体,如推断某种药品相比另一种药品的治愈效果)。对于无限总体,由于无法得出总体的具体数值,故此时总体=理论(如后文连续性矫正中可用理论频率直接代替总体频率);对于有限总体,总体个体数小且方便获取测量时,可以知道总体的具体数值。 | |||
样本的数值不一定等于总体的数值,总体的数值也不一定等于理论的数值——只能逐层估计。这时检验尤为重要。 | |||
==分布== | ==分布== | ||
| 第6行: | 第16行: | ||
====二项分布==== | ====二项分布==== | ||
公式:[[文件:二项分布公式.jpg| | 公式:[[文件:二项分布公式.jpg|二项分布公式|190x190像素]] | ||
事情要先从伯努利试验说起…… | 事情要先从伯努利试验说起…… | ||
| 第16行: | 第26行: | ||
二项分布还有一个更加亲民的形式:(p+q)<sup>n</sup> | 二项分布还有一个更加亲民的形式:(p+q)<sup>n</sup> | ||
当二项分布的np<5且n(1-p)<5时,直接使用二项分布检验;当5<np<30或5<n(1-p)< | 当二项分布的np<5且n(1-p)<5时,直接使用二项分布检验;当5<np<30或5<n(1-p)<30时,二项分布的图象逼近正态分布图像,可通过'''连续性矫正''',将其视作连续的正态分布进行计算;当np>30且n(1-p)>30时,二项分布和正态分布图像已几乎一致,可直接视作正态分布进行计算。 | ||
====泊松分布==== | ====泊松分布==== | ||
公式:[[文件:泊松分布公式.jpg| | 公式:[[文件:泊松分布公式.jpg|泊松分布公式|190x190像素]]<br> | ||
泊松分布是二项分布的极限,指的是(p+q)<sup>n</sup>中,p很小而n趋近于无穷大时的概率分布。 | 泊松分布是二项分布的极限,指的是(p+q)<sup>n</sup>中,p很小而n趋近于无穷大时的概率分布。 | ||
泊松分布的期望μ=λ,方差σ2=λ,标准差σ=根号下λ | 泊松分布的期望μ=λ,方差σ2=λ,标准差σ=根号下λ | ||
泊松分布的推导:[[文件:泊松分布的推导.jpg| | 泊松分布的推导:<br>[[文件:泊松分布的推导.jpg|泊松分布的推导|689x689像素]]<br>(关于那个打*号的红色已知式子,我不会推导(泣)有兴趣的烦请自行了解,,, | ||
(这个不用你推,因为这就是e的定义,就像你推不出来周长比直径为什么等于派一样)(——豪德👌) | |||
注意:虽然n趋于无穷大,且当λ不断增大时,泊松分布逼近正态分布,但泊松分布照样是个离散分布。 | 注意:虽然n趋于无穷大,且当λ不断增大时,泊松分布逼近正态分布,但泊松分布照样是个离散分布。 | ||
===连续的概率密度=== | ===连续的概率密度=== | ||
就生统而言,连续与离散最大的区别就是:离散分布中我们算的概率都是取到某个点的概率,而连续分布的“点”是没有意义的——毕竟在一连串连续的变量中,取得某一点的概率想也知道趋近于0——有意义的是“区间”。也就是说,求上下限间的累计概率,或者说求这段曲线围的面积,即计算积分。 | |||
====正态分布==== | ====正态分布==== | ||
| 第48行: | 第56行: | ||
H0为零假设,即无显著差异;H1(或HA)为备择假设,即有显著差异。 | H0为零假设,即无显著差异;H1(或HA)为备择假设,即有显著差异。 | ||
=== 连续性矫正 === | |||
===u检验和t检验=== | ===u检验和t检验=== | ||
u检验适用:大样本/小样本但总体方差一致(一般大小样本以30为界) | u检验适用:大样本/小样本但总体方差一致(一般大小样本以30为界)<br> | ||
[[文件:U检验的适用例.jpg| | [[文件:U检验的适用例.jpg|U检验的适用例|445x445像素]] | ||
t检验适用:小样本。和u检验非常类似,适用范围也一样(只是样本量n<30),但是曲线更胖——因为t检验样本量小,算出的方差相应更大。 | t检验适用:小样本。和u检验非常类似,适用范围也一样(只是样本量n<30),但是曲线更胖——因为t检验样本量小,算出的方差相应更大。 | ||
| 第64行: | 第74行: | ||
F检验算的是较大的方差与较小的方差的比值,再将这一数据查表检验显著性。注意:查表时较大方差对应的自由度和较小方差对应的自由度不要查反! | F检验算的是较大的方差与较小的方差的比值,再将这一数据查表检验显著性。注意:查表时较大方差对应的自由度和较小方差对应的自由度不要查反! | ||
若方差一致即不显著,就可以开始u检验或t检验了;若方差不一致即显著,则需要近似的u或t检验——这时是在方差上加权。以近似t检验为例: | 若方差一致即不显著,就可以开始u检验或t检验了;若方差不一致即显著,则需要近似的u或t检验——这时是在方差上加权。以近似t检验为例:<br> | ||
[[文件:近似t检验例.jpg| | [[文件:近似t检验例.jpg|近似t检验例|488x488像素]] | ||
===卡方检验=== | ===卡方检验=== | ||
| 第75行: | 第85行: | ||
注意:df=1时需要连续性矫正! | 注意:df=1时需要连续性矫正! | ||
举例:一个2×2列联表的卡方分析: | 举例:一个2×2列联表的卡方分析:<br> | ||
[[文件:2x2列联表卡方分析.jpg| | [[文件:2x2列联表卡方分析.jpg|2x2列联表卡方分析|470x470像素]] | ||
===方差分析=== | ===方差分析=== | ||
t检验和u检验都只能检验两组数据间差异的显著度,若涉及到3组及以上,便需要方差分析。t检验和u检验中方差齐且数据符合正态分布,故不需考虑组内(处理内)差异;而方差分析不一定数据符合正态分布,故数据间的差异涉及组内(处理内)差异与组间(处理间)差异。 | |||
====单因素方差分析==== | ====单因素方差分析==== | ||
====双因素方差分析==== | ====双因素方差分析==== | ||
2025年6月24日 (二) 02:58的版本
苯人数学不好,请大家帮忙指错并严厉批评(()
概念
总体·样本·理论
具有相同性质的个体所组成的集合称为总体……从总体中抽出的若干个体所构成的集合称为样本。——《生物统计学(第5版)》李春喜等
总体分为有限总体(其中个体数量有限,如一个班级的所有人)和无限总体(个体数量极大或无限,如一棉田中棉铃虫的总数;其中无限总体可以更抽象地拓展为理论总体,如推断某种药品相比另一种药品的治愈效果)。对于无限总体,由于无法得出总体的具体数值,故此时总体=理论(如后文连续性矫正中可用理论频率直接代替总体频率);对于有限总体,总体个体数小且方便获取测量时,可以知道总体的具体数值。
样本的数值不一定等于总体的数值,总体的数值也不一定等于理论的数值——只能逐层估计。这时检验尤为重要。
分布
离散的概率分布
二项分布
事情要先从伯努利试验说起……
伯努利试验说的这件事情只有两种结果:发生or不发生。显然,这两种结果的概率和p+q=1。当试验次数足够多,这个事件发生的频率就会趋近于它的概率——这正是所谓“大数定律”,也是我们能用实际得到的数据估算理论概率的基础。
二项分布,就是伯努利试验的拓展,是进行了多次重复的伯努利试验。——这里需要阐明一个概念:重复≠执行次数。重复指在一个试验中,将一个处理实施在两个及以上的试验单位上,这个试验单位的数量就是重复数。例如,一个人不停地抛硬币,这就是一个伯努利试验,其中P(X=正面)=1/2;而让3个人同时抛硬币,就成为了二项分布,我们可以算出在这个重复数下不同试验单位得到不同试验结果的概率,如P(X=两正一反)=C23×(1/2)2×(1/2)1
二项分布还有一个更加亲民的形式:(p+q)n
当二项分布的np<5且n(1-p)<5时,直接使用二项分布检验;当5<np<30或5<n(1-p)<30时,二项分布的图象逼近正态分布图像,可通过连续性矫正,将其视作连续的正态分布进行计算;当np>30且n(1-p)>30时,二项分布和正态分布图像已几乎一致,可直接视作正态分布进行计算。
泊松分布
公式: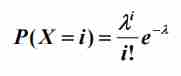
泊松分布是二项分布的极限,指的是(p+q)n中,p很小而n趋近于无穷大时的概率分布。
泊松分布的期望μ=λ,方差σ2=λ,标准差σ=根号下λ
泊松分布的推导:
(关于那个打*号的红色已知式子,我不会推导(泣)有兴趣的烦请自行了解,,,
(这个不用你推,因为这就是e的定义,就像你推不出来周长比直径为什么等于派一样)(——豪德👌)
注意:虽然n趋于无穷大,且当λ不断增大时,泊松分布逼近正态分布,但泊松分布照样是个离散分布。
连续的概率密度
就生统而言,连续与离散最大的区别就是:离散分布中我们算的概率都是取到某个点的概率,而连续分布的“点”是没有意义的——毕竟在一连串连续的变量中,取得某一点的概率想也知道趋近于0——有意义的是“区间”。也就是说,求上下限间的累计概率,或者说求这段曲线围的面积,即计算积分。
正态分布
正态分布N(μ,σ2)的分布状态是多数变量围绕在平均值左右,由平均值到分布两侧变量数减少。
参数:μ总体平均数,σ2总体方差;当x=μ时,f(x)有最大值;当x-μ的绝对值相等时,f(x)值也相等;f(x)以x轴为渐近线,x取值区间(-∞,+∞)。
一般使用标准正态分布N(0,1),因为国赛发的CASIO 991CN CW只能算这个。对于非标准的正态分布,可进行标准化变换:u=(x-μ)/σ
数据:x≤1时累计概率P(1)=0.84134,0≤x≤1时累计概率Q(1)-0.34134,x≥1时累计概率R(1)=0.15866,其中P(1)+R(1)=1
检验方法
检验分假设检验和参数估计。假设检验中参数已知,参数估计中参数未知。
H0为零假设,即无显著差异;H1(或HA)为备择假设,即有显著差异。
连续性矫正
u检验和t检验
u检验适用:大样本/小样本但总体方差一致(一般大小样本以30为界)

t检验适用:小样本。和u检验非常类似,适用范围也一样(只是样本量n<30),但是曲线更胖——因为t检验样本量小,算出的方差相应更大。
让我们对着u检验和t检验近乎一样的公式理一下思路:分子上样本均值-总体均值,很显然是样本与总体间的差异;分母上标准误,那便可看作以标准误为单位,衡量样本与总体间的差异(或是两组间的差异,etc.)——显然,标准误这一标尺需要相等。这也正是所谓的:u检验和t检验都要求方差齐性。
于是需要一个新的检验方式:F检验。
F检验
F检验算的是较大的方差与较小的方差的比值,再将这一数据查表检验显著性。注意:查表时较大方差对应的自由度和较小方差对应的自由度不要查反!
若方差一致即不显著,就可以开始u检验或t检验了;若方差不一致即显著,则需要近似的u或t检验——这时是在方差上加权。以近似t检验为例:

卡方检验
分适合性检验、独立性检验。
卡方检验的自由度df=(行数-1)(列数-1)
注意:df=1时需要连续性矫正!
方差分析
t检验和u检验都只能检验两组数据间差异的显著度,若涉及到3组及以上,便需要方差分析。t检验和u检验中方差齐且数据符合正态分布,故不需考虑组内(处理内)差异;而方差分析不一定数据符合正态分布,故数据间的差异涉及组内(处理内)差异与组间(处理间)差异。