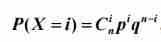生物统计漫谈
苯人数学不好,请大家帮忙指错并严厉批评(()
概念
基本统计参数
平均数众数中位数初中学过了不讲()这里介绍一下自由度、方差和标准误。
自由度(df)
计算某一统计量时,取值不受限制的变量个数。通常df=n-k,其中n为样本数量,k为被限制的条件数或变量个数。在χ2列联表中,df=(行数-1)x(列数-1)
方差
一般算式初中学过不讲(而且卡西欧统计直出)讲一下方差另一个更常用公式的推导:

↑这个是样本方差,由于由实际观察数得出,分母上是自由度df;若是总体方差σ2,分母上是样本量n。
标准差(SD)
方差的平方根。
标准误(SE)
样本均值分布的标准差,反映抽样误差的大小,表明样本均值对总体均值的代表性 。计算公式为总体标准差除以样本量的平方根(σ/√n)。
总体·样本·理论
具有相同性质的个体所组成的集合称为总体……从总体中抽出的若干个体所构成的集合称为样本。——《生物统计学(第5版)》李春喜等
总体分为有限总体(其中个体数量有限,如一个班级的所有人)和无限总体(个体数量极大或无限,如一棉田中棉铃虫的总数;其中无限总体可以更抽象地拓展为理论总体,如推断某种药品相比另一种药品的治愈效果)。对于无限总体,由于无法得出总体的具体数值,故此时总体=理论(如后文连续性矫正中可用理论频率直接代替总体频率);对于有限总体,总体个体数小且方便获取测量时,可以知道总体的具体数值。
样本的数值不一定等于总体的数值,总体的数值也不一定等于理论的数值——只能逐层估计。这时检验尤为重要。
错误
α错误(第一类错误):拒绝真实的H0假设,即假阳性/拒真风险;
β错误(第二类错误):未拒绝错误的H0假设,即假阴性/纳伪风险。
两类错误在样本量固定时呈负相关,可通过调整显著性水平α值来权衡这两类错误。
显著性水平α数值越小(即检验越严格),一类错误概率越低,二类错误概率越高。
增大样本量可同时降低犯两类错误的概率。
二类错误的发生率同时取决于样本与实际均值的误差即|μ0-μ1|,|μ0-μ1|减小会导致假阴性发生率大幅增加,亦即二类错误概率增加。
分布
离散的概率分布
二项分布
事情要先从伯努利试验说起……
伯努利试验说的这件事情只有两种结果:发生or不发生。显然,这两种结果的概率和p+q=1。当试验次数足够多,这个事件发生的频率就会趋近于它的概率——这正是所谓“大数定律”,也是我们能用实际得到的数据估算理论概率的基础。
二项分布,就是伯努利试验的拓展,是进行了多次重复的伯努利试验。——这里需要阐明一个概念:重复≠执行次数。重复指在一个试验中,将一个处理实施在两个及以上的试验单位上,这个试验单位的数量就是重复数。例如,一个人不停地抛硬币,这就是一个伯努利试验,其中P(X=正面)=1/2;而让3个人同时抛硬币,就成为了二项分布,我们可以算出在这个重复数下不同试验单位得到不同试验结果的概率,如P(X=两正一反)=C23×(1/2)2×(1/2)1
二项分布还有一个更加亲民的形式:(p+q)n
当二项分布的np<5且n(1-p)<5时,直接使用二项分布检验;当5<np<30或5<n(1-p)<30时,二项分布的图象逼近正态分布图像,可通过连续性矫正,将其视作连续的正态分布进行计算;当np>30且n(1-p)>30时,二项分布和正态分布图像已几乎一致,可直接视作正态分布进行计算。
二项分布的期望为np(很好理解),方差为npq。
泊松分布
公式: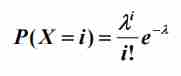
泊松分布是二项分布的极限,指的是(p+q)n中,p很小而n趋近于无穷大时的概率分布。
泊松分布的期望μ=λ,方差σ2同样也是λ
实际上λ就是泊松分布的np值,由于q趋近于1,npq趋近于np。
泊松分布的推导:
(关于那个打*号的红色已知式子,我不会推导(泣)有兴趣的烦请自行了解,,,
(这个不用你推,因为这就是e的定义,就像你推不出来周长比直径为什么等于π一样)(——豪德👌)
注意:虽然n趋于无穷大,且当λ不断增大时,泊松分布逼近正态分布,但泊松分布照样是个离散分布。
负二项分布
负二项分布同样来自多次独立的伯努利实验。区别在于,负二项分布衡量第k次成功时实验次数为i的概率。
负二项分布的期望为k/p(同样很好理解),方差为k(1-p)/p2。
几何分布:特殊的负二项分布,其k=1。
值得注意的是,生态学中种群的空间分布概率符合负二项分布,k值可作为衡量指标,k越小,种群越倾向于集群分布。
连续的概率密度
就生统而言,连续与离散最大的区别就是:离散分布中我们算的概率都是取到某个点的概率,而连续分布的“点”是没有意义的——毕竟在一连串连续的变量中,取得某一点的概率想也知道趋近于0——有意义的是“区间”。也就是说,求上下限间的累计概率,或者说求这段曲线围的面积,即计算积分。
正态分布
正态分布N(μ,σ2)的分布状态是多数变量围绕在平均值左右,由平均值到分布两侧变量数减少。
参数:μ总体平均数,σ2总体方差;当x=μ时,f(x)有最大值;当x-μ的绝对值相等时,f(x)值也相等;f(x)以x轴为渐近线,x取值区间(-∞,+∞)。
一般使用标准正态分布N(0,1),因为国赛发的CASIO 991CN CW只能算这个。对于非标准的正态分布,可进行标准化变换:u=(x-μ)/σ
数据:x≤1时累计概率P(1)=0.84134,0≤x≤1时累计概率Q(1)=0.34134,x≥1时累计概率R(1)=0.15866,其中P(1)+R(1)=1
检验方法
检验分假设检验和参数估计。假设检验中参数已知,参数估计中参数未知。
H0为零假设,即无显著差异;H1(或HA)为备择假设,即有显著差异。
为什么我们可以用样本估计总体?
大数定律:对于一系列独立同分布(服从相同分布且相互独立)的随机变量,变量均值的极限等于所属分布的数学期望。
为什么前述的任意离散分布最终都可以逼近正态分布?
中心极限定律:对于一系列独立同分布的随机变量,若其所属分布具有固定且有限的数学期望和方差,则当变量数n趋近于正无穷时,变量服从标准正态分布。
连续性矫正
u检验和t检验
u检验适用:总体方差σ2已知,样本平均数的分布均服从正态分布,故大样本/小样本(一般样本量n≥30为大样本,反之小样本)都可;或总体方差σ2未知但为大样本。

t检验适用:总体方差σ2未知的小样本。和u检验非常类似,但是曲线更胖——因为t检验样本量小,算出的方差相应更大。
让我们对着u检验和t检验近乎一样的公式理一下思路:分子上样本均值-总体均值,很显然是样本与总体间的差异;分母上标准误,那便可看作以标准误为单位,衡量样本与总体间的差异(或是两组间的差异,etc.)——显然,标准误这一标尺需要相等。这也正是所谓的:u检验和t检验都要求方差齐性。
于是需要一个新的检验方式:F检验。
F检验
F检验算的是较大的方差与较小的方差的比值,再将这一数据查表检验显著性。注意:查表时较大方差对应的自由度和较小方差对应的自由度不要查反!
若方差一致即不显著,就可以开始u检验或t检验了;若方差不一致即显著,则需要近似的u或t检验——这时是在方差上加权。以近似t检验为例:

卡方检验
分适合性检验、独立性检验。
卡方检验的自由度df=(行数-1)(列数-1)
注意:df=1时需要连续性矫正!
方差分析
t检验和u检验都只能检验两组数据间差异的显著度,若涉及到3组及以上,便需要方差分析。t检验和u检验中方差齐且数据符合正态分布,故不需考虑组内(处理内)差异;而方差分析不一定数据符合正态分布,故数据间的差异涉及组内(处理内)差异与组间(处理间)差异。严格地说,方差分析指的是“证明差异存在”的方法,后续的“两两进行比较”则是多重比较。
根据分析因素(处理)的多少,可分为单因素方差分析、双因素方差分析及以上。
单因素方差分析
计算平均数差数的标准误时,Se2代的是处理内的方差,这样算出的标准误就代表了单纯在处理内(由于重复)造成的与总体均值的差异。用这个值对查表得到的t值加权,得出仅由于重复造成的差异的上界,也就是达到差异显著的最小差数(即LSD值),若两组数据平均值的差超过这一值,则说明这两组间有显著/极显著差异。
例子中是组内重复数不同的单因素方差分析,若组内重复数相同那更简单了只需算C值时,分子是所有重复的总和T的平方,分母是组数k × 每组重复数n(本质是一样的,只是不用分开算,计算器上更少打一点()
例子中用的多重比较方法是LSD法(最小显著差异法),除此之外还有LSR法(最小显著极差法),LSR法又可分为新复极差检验(又称Duncan法、SSR法)和q检验(又称SNK检验)。以下简述其他方法思路:
新复极差检验:当样本容量相等时,通过计算不同组均值的极差(最大值-最小值),并与临界值LSRα=SSRα·√(Se2/n)(SSRα从Duncan’s极差表中查出,与组数p、自由度ν和显著性水平α相关)比较,从而判断差异是否显著。
q检验(SNK检验):以统计量q的概率分布为基础,与新复极差检验方法基本一致,将极差与临界值LSRα=q·极差/√(Se2/n)(q从q值表中查出)比较,从而判断差异是否显著。
在样本数(处理数)k=2时,LSD法、SSR法、q法的显著尺度是相同的。当k≥3时,3种检验的显著尺度便不相同,LSD法最低、SSR法次之、q法最高,即这3种检验⽅法的检验尺度关系为LSD法 ≤ SSR法 ≤ q法。