第三章 什么造就了视力眼?
眼睛是感觉器官中独一无二的,因为我们对视觉的物理和化学了解足够多,能够相当肯定地说出为什么眼睛是这样构造的。当然,眼睛不是像设计照相机或望远镜那样经过设计的,而是经过数百万年的进化而来的。然而,进化和技术都必须遵循同一套物理规则。例如,成像透镜必须利用透明高折射率材料的折射原理制成,无论这种透镜是在章鱼或鱼中进化而来的,还是由徕卡或尼康设计的。不同之处在于材料:透镜通常由蛋白质而不是玻璃构成,反射镜由鸟嘌呤层片而不是银制成。生物与技术的区别在于化学而不是物理。在本章中,我们将探讨眼睛进化的这些物理限制。我们将大胆地宣称,以光学工程师评估新摄像机的方式对待眼睛是明智的。我们可以说出大多数组件的用途以及它们的性能,还可以建立判断眼睛整体性能的标准。因此,本章旨在成为解释眼睛结构的工具包,并为比较不同类型的眼睛的性能提供基础,这些性能将成为后续章节的主题。
眼睛提供有关环境中光分布性质的信息。对于鹰来说,这些信息需要非常精细,但对于扁虫来说,它可能很粗糙。虽然我们不能说扁虫的简单色素杯眼在进化意义上不如鹰眼成功,但我们仍然可以说鹰眼更好,因为它能够向其携带者提供大量信息。如果我们要使用“信息供应”作为判断眼睛质量的基础,尽管这种说法并不严谨,那么我们应该使用什么标准呢?我们暂时不考虑区分波长和偏振平面的能力;这些特征更多的是受体的分子组织,而不是眼睛本身的结构(见第 2 章)。人们普遍认为,眼睛功能有两个特征,它们概括了眼睛的性能,并且与眼睛的光学类型无关。它们是分辨率resolution和灵敏度sensitivity。分辨率是指眼睛根据光线的来源方向分解光线的精度。这是光学器件提供的图像质量和视网膜探测器马赛克的精细度的结合。灵敏度是指眼睛将足够的光线传送到受体的能力,以便受体充分利用眼睛的潜在分辨率。对于生活在昏暗环境中的动物来说,灵敏度与分辨率同样重要。

在详细研究眼睛的哪些特征有助于提高性能之前,我们首先简要了解一下分辨率和灵敏度相互作用的方式,以及两者为何重要的原因。图 3.1 是一只假想的眼睛,分辨率相当差,图像昏暗,旨在以夸张的形式显示所有眼睛都会面临的问题。眼睛外的两个点光源通过晶状体聚焦在视网膜上,在那里它们产生的光分布不再是点状的,而是模糊的,并分散在几个受体上(模糊圈)。造成这种扩散的原因有很多。例如,光学系统可能无法将所有光线集中到一个焦点(像差),或者光线可能被眼睛的介质散射。即使眼睛在这些方面是完美的,仍然存在一个基本的模糊源,即衍射diffraction,这是不可避免的,它源于光的波动性(见下面的图 2.1 和 3.5)。这将在本章后面讨论,但基本上,眼睛的孔径与光的波长相比越小,问题就越严重,因此,在昆虫复眼的微小光学系统中,衍射尤其严重(第 7 章)。这些缺陷导致的模糊程度限制了各种图像的质量,从而也决定了视网膜马赛克的精细程度。视网膜上没有任何一点的受体比构成图像的模糊圆圈小得多。粗略地说,当两个受体占据点源图像中光分布的一半宽度时,图像中包含的所有信息都会被提取出来,大致如图 3.1 所示。因此,图像质量越差,接收图像提供的所有信息所需的受体数量就越少。比这更粗糙的马赛克会浪费图像细节(“欠采样undersample”),而更精细的马赛克将具有比必要更多的受体(“过采样oversampling”),因此存在明显的最佳值。大多数眼睛确实表现出图像质量和视网膜“颗粒”之间的预期匹配。
图 3.1 还通过显示(黑点)每个受体从图像中捕获多少光子来说明低光照水平的影响。光是量子的,最小的光能包光子在被视紫红质分子捕获时是不可分割的:它要么存在,要么不存在(第 2 章)。这意味着在低光照水平下存在很大的统计不确定性,在图 3.1 中表示为受体中捕获的光子数量可变,每个受体都接收到相同的平均光量。如果有更多的光子,那么光子数分布将越来越类似于光学分布,但如果光子数较少,情况将变得更糟,只有偶尔的光子到达成像每个点源的任何受体。因此,低光照水平会通过引入光子数的不确定性来破坏图像。人们可以认为这会产生一种统计模糊,这会增加由衍射或不完美光学引起的模糊,并且对眼睛的分辨能力产生类似的有害影响。在低水平下,这通常意味着使用大型受体以获得合理的统计光子样本比使用小型受体精细地采样图像更好。我们将反复遇到这种分辨率和灵敏度之间的权衡,特别是在必须在一定光照水平范围内运作的动物中。
我们已经看到,光的波和粒子方面都会影响眼睛的性能。它的波动性对图像质量施加了根本限制,并且正如我们稍后将看到的,对受体尺寸也施加了根本限制;它的量子性质决定了可以测量光的确定性。考虑到这些限制,本章的其余部分将用于探索眼睛的功能和限制其功能的特征。
分辨率
视网膜采样频率
眼睛的两个特征限制了在明亮光线下可以分辨的细节,即受体马赛克的精细度和图像的质量。我们如何才能最好地比较这两个截然不同的属性的效果?事实证明,可以应用于两者的最佳测量方法之一是它们分辨暗条和亮条光栅的能力。在受体马赛克的情况下,一个公认的发现是,如果每个相邻的暗条和亮条的图像落在单独的受体上,则可以正确分辨光栅。这意味着图像中可分辨最精细光栅的周期(两个相邻的暗条或亮条中心之间的距离)等于受体间距的两倍。
当处理眼睛外部的物体和眼睛内部的图像时,处理角度而不是距离通常最方便,因为相同的角度测量适用于两者。在我们自己的单腔眼中,眼睛中总有一个点称为 nodal point,光线通过该点时不会被晶状体弯曲。例如,在用简单弯曲的角膜形成图像的眼睛中,节点将位于角膜表面的曲率中心,因为穿过该点的光线将以直角与表面相遇,因此不会因折射而弯曲。节点的意义在于,人们可以通过它画出连接物体和图像点的直线,从而通过相似三角形原理直接计算出物体和图像的相对大小(图 3.2a)。距离眼睛 U 处尺寸为 O 的小物体在节点处形成一个角 α = O / U 弧度(弧度是圆心处一个半径长度的圆弧所形成的角度:1 弧度 = 180°/π,或 57.3°),在眼睛内部,图像 I 在节点处对角 α。对于我们的目的而言,焦距 (f) 的最佳定义是从节点到远处点图像的距离。然后等式:
O/U =α=I/f (3.1)
总结了物体与图像之间的关系,前提是物体距离很远。一个特别重要的角度是受体间角度 s/f ,因为它决定了图像采样的精细度,其中 s 是受体中心的间距。符号 Δ ϕ 将用于表示此角度(图 3.2b)。
现在,我们可以将方程 (3.1) 应用于眼睛的光栅分辨率。最精细的可分辨光栅在视网膜上的周期为 2 s。以眼睛内部图像空间或外部物体空间的角度表示,即 2 s / f 弧度。通常,说光栅的空间频率(周期的倒数,以每弧度的周期数表示)更有用,因为频率会随着分辨率的提高而增加,而周期会减少。视网膜对图像进行采样的空间频率是采样频率νs,因此:
采样频率νs =f /(2s ) =1/(2 Δϕ) (3.2)
该方程表明,有两种方法可以增加采样频率,从而提高眼睛的分辨率。焦距 f 可以增加,或者受体间距 s 可以减小。不可能将 s 减小到 2 μm 以下,因为比这更窄的受体会漏光,这一点后面会讨论。一旦达到这个极限,就像许多动物一样,改善情况的唯一方法就是增加焦距,而这必然意味着眼睛要更大。
表 3.1 显示了各种动物眼睛的分辨率,用受体间角度 Δ φ 和采样频率νs 来表示。它们的范围从采样频率约为每弧度 1 个周期的扁虫到每弧度约 8000 个周期的老鹰。
| 物种 | 最大可解析空间频率(每弧度周期数) | 等效受体间角度(度) | 方法 | 参考文献 |
|---|---|---|---|---|
| Aquila(鹰) | 8022 | 0.0036 | B, A | 1 |
| 人(中央凹) | 4175 | 0.007 | B, A | 2 |
| 章鱼(Octopus) | 2632 | 0.011 | A | 2 |
| 跳蛛(Portia) | 716 | 0.04 | A | 3 |
| 猫(Cat) | 573 | 0.05 | B | 4 |
| 金鱼(Goldfish) | 409 | 0.07 | B | 5 |
| 蜻蜓(Aeschna) | 115 | 0.25 | A | 2 |
| 地鼠(Hooded rat) | 57 | 0.5 | B | 4 |
| 工蜂(Worker bee) | 30 | 0.95 | B, A | 2 |
| 螃蟹(Leptograpsus) | 19 | 1.5 | A | 6 |
| 扇贝(Pecten) | 18 | 1.6 | B, A | 2 |
| 狼蛛(Lycosa) | 16 | 1.8 | A | 5 |
| 海螺(Littorina) | 6.5 | 4.5 | A | 2 |
| 果蝇(Drosophila) | 5.7 | 5 | B, A | 2 |
| 鲎(Limulus) | 4.8 | 6 | A | 6 |
| 鹦鹉螺(Nautilus) | 3.6 | 8 | B, A | 2 |
| 深海等足类(Cirolana) | 1.9 | 15 | A | 6 |
| 涡虫(Planaria) | 0.8 | 35 | A | 2 |
A,基于解剖学。B,基于动物行为学。如果行为学得出的分辨率低于受体间距,行为学结果将被使用。无脊椎动物的pooling可能降低分辨率。
The optical cut-off
场景中的细节越精细,解析就越困难;远处的树叶在整体纹理中失去了其特征。从光学角度来看,我们可以认为世界是由一系列空间频率的光栅组成的。显然,代表最精细细节的最高空间频率无法在视觉过程中保留下来。这可能是因为视网膜马赛克无法完全采样它们,正如我们已经讨论过的,但这不是唯一的原因。眼睛的光学系统也会衰减,并最终切断最高频率。说明这一点的最佳方法之一是测量contrast ( modulation ) transfer function(图3.3).这张图显示了光栅的对比度在穿过透镜时如何降低,作为空间频率的函数。[对比度在第 2 章中定义:对于光栅,它是亮条 ( Imax) 和暗条 ( Imin) 的强度差除以它们的和,即对比度 = ( Imax− Imin)/( I max+ Imin)。除以 ( Imax+ Imin) 可使对比度与整体光水平无关]。光学系统的效果始终是降低图像中的对比度,与产生图像的物体光栅相比(插图,图 3.3),并且这种降低对于最高的空间频率最大。最终,如图 3.3 所示,达到图像中完全没有对比度的空间频率,这称为 optical cut-off frequency ( vco ).。

衍射极限
是衍射设定了截止(cut-off)频率。其他光学缺陷,例如未正确聚焦,可能会导致对比度在所有空间频率下降低,但它们不一定会改变截止点本身。因此,衍射对于理解图像质量和眼睛设计至关重要。它源于光的波动性质。当来自远处点物体(例如星星)的光到达镜头时,平行光线会因折射而弯曲,从而汇聚在图像平面的单个焦点上。另一种更准确的描述是,恒星发出的光以wavefront(“射线”是 arbitrary lines at right angles to this front,见图 2.1a)的形式到达透镜。通过透镜时,wavefront的中心区域比边缘区域延迟更多,因为它穿过更多的光学致密材料。结果是新出现的wavefront不再是平坦的,而是弯曲成部分球形,以焦点为中心并向焦点前进(插图,图 3.4)。在焦点处,wavefront的各个部分相遇,当它们相互穿过时,它们会干涉。彼此同相的分量将加强,而完全异相的分量将抵消,从而在焦点处产生一个不是点的图案(如射线理论所假设的那样),而是衍射图案。在点源物体和圆形孔径的简单情况下,该图案具有一个中心亮点,称为艾里斑(以其发现者命名),其形状如图3.4所示。

衡量艾里斑大小的一个方便方法是其半宽,即半峰强度处的宽度 (w)(图 3.4)。事实证明,这几乎与方框 3.1 中讨论的第一个暗环的距离相同。对于焦距为 f 的透镜,其公式为:
w = fθ=fλ/D (3.3)
w 的值越大,点的图像越宽,或者更通俗地说,图像越模糊。粗略地说,物体的图像
方框 3.1 艾里衍射图案的起源
光学教科书中提供了艾里衍射图案的完整推导,但它对于理解视觉极限非常重要,因此需要指出它是如何产生的。在图 3.5a 中,来自会聚wavefront的两条光线在焦点区域发生干涉。它们来自光圈每半部分中心的两个点 X 和 Y(整个光圈可以看作是由一系列相似的点对组成)。然后我们问一个问题:“我们必须离焦点多远才能使图像变暗?”这个“第一个暗环”可以看作是定义点物体图像的边缘。对于图像中心的点 A,光圈中 X 和 Y 的距离相同,因此波将同相,它们将发生相长干涉,并且
图 3.5 衍射和图像。 (a) 构造以说明为什么点源的图像在远离轴时变暗。当从光圈的两个半部分到达图像的光线之间的路径长度相差半个波长 (λ/2) 时,就会发生相消干涉,B 处的图像将变暗。图像中与距离 AB 相对应的角度为 θ,对于圆形孔径等于 1.22 λ/ D (图 3.4)。
(b) 干涉图样说明了为什么大孔径 (右) 产生的“艾里斑”比小孔径 (左) 产生的“艾里斑”更窄。
55
大于 w 的图像将被解析,但较小的图像则不会,因为它们被模糊了。 这反映在对比度传递函数 (图 3.3) 中,因为最精细的可解析空间频率 - 截止频率 ( vco ) - 只是艾里斑半宽的倒数:- w D f co
截止频率 ( ) 1/ / ( ) n l = = (3.4)
换句话说,光学系统可以解析的最精细光栅的周期等于点源图像的半宽。
公式 (3.3) 表明,决定分辨率的角图像大小 θ (= w / f ) 与光圈直径成反比。镜头越大,θ 值越小,分辨率越好。这是一个重要而又奇怪的违反直觉的结论。人们可能会认为,扩大光学系统并增大光圈会导致像盘的宽度成比例增加;但事实恰恰相反 (图 3.5b)。这就是为什么天文学家需要大型望远镜来分辨小而紧密的恒星。同样,这也是为什么昆虫的眼睛 (其镜头直径以微米为单位) 的分辨率如此之差的原因。A 会很亮。然而,在点 B 处,距离不再相同,
如果从 X 到 Y 的路径长度差等于
光波长的一半(λ/2),则两束光将完全不同相位
并发生相消干涉,因此 B 处将显得较暗。在图 3.5 中,我们可以看到,汇聚在 B 处的三角形与汇聚在 A 处的三角形不同,前者倾斜了角度 θ,并且在其一条边上有一个额外的短线段
z。z 的长度将决定在 B 处发生哪种干涉(相消干涉或相消干涉)。z 与另一个包含 X 和 Y 的三角形以及汇聚在 B 处的三角形的底边共享,后者也倾斜了角度 θ。X 和 Y 之间的距离是光圈直径的一半(λ/2),因此以弧度表示的 θ 等于 z ÷ D /2。如果 B 处要显得较暗,z 必须等于 λ/2。用该值代替 z 可得出 θ =λ/ D 。现在,这是标记亮图像边缘的暗环相对于镜头中心的角度位置。它可以通过乘以焦距转换为图像平面中的距离,如公式 (3.1) 所示。尽管进行了简化假设,但该结果非常接近 Airy 的完整计算,对于具有圆形光圈的镜头,该计算得出 θ = 1.22 λ/ D 。框 3.1 Airy 衍射图案的起源(续)56 动物的眼睛例如,我们可以使用公式 (3.3) 和公式 (3.4) 来比较人类和蜜蜂眼睛的理论分辨率极限。在日光下,人眼的瞳孔大约为 2 毫米宽,因此,对于 0.5 微米(蓝绿色)的波长,θ 为 0.00025 弧度,即 0.014°,或 0.86 弧分。相应的截止频率为每度 70 个周期,非常接近视网膜马赛克的采样频率,大约为每度 60 个周期(vs,公式 3.2)。然而,蜜蜂的复眼的刻面直径只有 25 微米。这比人类瞳孔小 80 倍,因此分辨率必须差 80 倍,θ 约为 1.1°。为了感受一下这意味着什么,伸出手臂,小指甲覆盖大约 1°。用这个例子很容易想象,与我们的视觉相比,蜜蜂的视觉世界会多么模糊。
其他光学缺陷
虽然衍射是分辨率的最终极限,只能通过增大眼球光圈来改善分辨率,但还有其他几种方法可能会损害分辨率。最重要的是聚焦、球面像差和色差,它们都发生在动物的眼睛里(图 3.6)。近处的物体比远处的物体更远地聚焦在镜头上,因此,对于大眼睛来说,光学系统能够以某种方式适应物体距离尤其重要。这种调节过程可以通过改变晶状体的度数(在人身上)或移动晶状体(在鱼身上)来实现。失焦的图像质量会下降,因为点源会在视网膜上产生“模糊圈”,就像艾里斑一样,会降低对比度传递函数(图 3.3)。
球面像差是指由于简单的球面无法将所有光线汇聚到单一焦点而产生的模糊现象。
离镜头轴最远的光线折射过多,靠近轴的光线最终会聚在焦点前面,从而再次形成比艾里斑更大的模糊圈。这对生物医学来说可能是一个严重的问题鱼眼的镜片通常都是球形的,但动物可以通过两种方式绕过它。
他们可能会使光学表面非球形,事实上,人类的角膜不是球形的,而是双曲面的,以避免这个问题。
一种常见的替代方法是制造一个光学上不均匀的镜片,就像玻璃一样,但折射率从中心(高)到边缘(低)呈梯度变化。结果是镜片的外部区域比玻璃镜片的折射要少,并且通过正确的折射率梯度,所有成像光线都可以集中到一个点。鱼眼镜片具有这种结构,并具有相应的出色光学性能,
聚焦缺陷
球面像差
图 3.6 其他光学缺陷。顶部:视网膜上的图像不清晰。
中间:球面像差,其中外部光线比轴附近的光线更靠近镜片聚焦。
底部:色差,其中
不同波长(红色和蓝色)
聚焦在不同的距离。
在每种情况下,结果都是一个模糊
圆圈,由于衍射而增加了模糊。
色差
模糊
圆圈
57
视网膜
B
R
R
B
自 19 世纪 80 年代 Matthiessen 的研究以来就已为人所知(参见第 4 章)。
人类晶状体从我们的鱼类祖先那里继承了这种设计,并以这种方式校正自己的球面像差。因此,人眼既有非球面(角膜)校正机制,也有不均匀(晶状体)校正机制。
色差的原因是短波长蓝光比长波长红光折射更强烈。这发生在生物材料中,就像在玻璃中一样,这意味着人眼中的蓝色图像几乎比红色图像提前 0.5 毫米。似乎没有一种动物的眼睛能够模仿早期望远镜制造者通过使用多种材料组合来制造消色差透镜的成就。然而,还有其他解决方案。人类通过仅使用光谱中间相对较窄的波长范围来实现高敏锐度视觉,从而部分避免了这个问题,因此我们在光谱蓝色端的分辨率很差——只不过是“色彩清洗”。鱼和其他一些脊椎动物更微妙一些,它们的晶状体有多个焦距。这确保了每种视锥细胞至少有一部分到达它的光具有聚焦图像(参见第 4 章)。与衍射不同,在衍射中眼睛的大小是一种优势,而这些其他问题随着眼睛变大而变得更糟。原因是像差引起的模糊圈会随着眼睛的焦距而变化,因此,如果未进行校正,焦距为 1 厘米的眼睛的模糊圈会比焦距为 1 毫米、设计相同的眼睛的模糊圈大 10 倍。但是,受体通常不会随着焦距而变化,而是无论眼睛大小如何,其直径都大致相同。因此,眼睛的潜在分辨率(以受体间角度 Δ ϕ (= s / f ) 衡量)应该会随着焦距的增加而提高。但是,只有将焦点缺陷和其他像差最小化,模糊圈才不会比受体直径大很多,才能做到这一点。对于焦距较短的结构,例如焦距约为 100 μm 的并列复眼的小眼,与衍射相比,这些缺陷可以忽略不计;没有昆虫需要聚焦眼睛的机制。焦距为 1 毫米时,它们变得明显,而焦距达到 1 厘米时,它们就变得严重了。在所有脊椎动物以及头足类软体动物中,这三种光学问题都以某种方式得到解决。可收缩瞳孔在处理光学缺陷时尤为重要,因为它可用于在衍射(宽瞳孔)和像差(小瞳孔)之间达成适当的折衷。这种折衷会随着强度而变化,因为明亮的光线有利于高敏锐度,但在昏暗的光线下,首要任务是获得足够的光子数(另见第 5 章,图 5.10)。光感受器光学
到目前为止,本节仅讨论了光学图像质量方面的分辨率,但眼睛传输图像所含信息的能力还取决于光感受器的大小,以及我们已经讨论过的它们的间距。如果受体的直径比眼睛可以分辨的最细光栅中的线更窄,那么它将能够准确测量该线的强度(严格来说是照度,见图 2.2)。但是,如果它更宽,它将吞没该线和其他几条线,并发出光栅未解析的平均强度信号。因此,对于功能是在日光下很好地分辨的眼睛来说,狭窄的受体是必不可少的,而这确实是发现的。人眼中的视锥细胞直径约为 2 μm,这几乎
正好是刚分辨出的 70 cyc 光栅中一条线的宽度每度 100 微米。蜜蜂眼中的受体宽度也约为 2 微米,但由于蜜蜂眼中一个面的焦距非常短(约 100 微米),因此所涉及的角度要大得多,刚好超过 1°(公式 3.1 中的 α)。与人类一样,这接近衍射所施加的光学分辨率极限。为什么受体不能更窄呢?正如我们刚刚看到的,眼睛的分辨能力取决于单个受体所对的角度等。由于它等于 s / f 弧度(图 3.2),因此似乎可以通过减小焦距(f)来缩小眼睛,而不会降低分辨率,前提是可以同时减小受体直径(d≈s)。然而,这并没有发生。脊椎动物和昆虫中最窄的受体大约有 1 微米宽。主要原因似乎是,当光受体的宽度开始接近可见光波长(0.3-0.8 微米)时,受体不再能够通过全内反射将光保持在其中(图 3.7a),并且变得效率低下且“泄漏”。与衍射一样,这是一种与光的波动性质相关的现象。在狭窄的光导纤维中,也就是光感受器,被捕获的光形成干涉图案,称为波导模式(图 3.7b,图 3);这些模式的性质类似于风琴管中的驻波,即它们的声学等效物。这些模式下的光分布不均匀,特别是在最窄的光纤中发现的单模,其能量的很大一部分实际上在光纤之外(Snyder 1979 和 van Hateren 1989 对此进行了解释)。这种光不仅不能被光纤内的视紫红质分子捕获,而且还可以被外部结构(如筛选色素颗粒)吸收,甚至被相邻的受体吸收。当这种情况发生时,受体之间就会发生“串扰”,分辨率就会受到影响。实际的后果是,使用小于 1 微米的受体没有任何好处,这反过来又为焦距设置了下限,从而为给定分辨率的眼睛的大小设置了下限。在窄受体中,第一波导模式保留了入射光的偏振,这意味着受体的偏振特性主要由光色素分子在细胞膜中的填充方式决定。即使在更宽的受体中也是如此。(a)qcrit 图 3.7 受体光学。 (a) 在宽接收器中(左图),光被全内反射捕获。
这种情况只发生在临界角(θ crit)以下,
该角由 arcsin(n 1
/n 2
) 给出,其中 n 1
和
n 2
是接收器外部和内部的折射率,其典型值为 1.34 和 1.36–1.40。 (b) 在非常窄的接收器(直径 < 2 μm)中,光表现为波导模式,并且具有一些在结构外传播的分布。
这可以被相邻的接收器捕获(点画)。
n1
(b)
n2
60 动物眼睛
接收器,其中全内反射在一定程度上使离轴光去极化(见图 2.7)。
在脊椎动物的视网膜中,光线必须穿过内视网膜的各个神经层才能到达视杆细胞和视锥细胞,尽管这些层是透明的,但它们在光学上并不均匀,因此会导致一些光散射。看来,在哺乳动物中,Müller 细胞(从玻璃体到受体,横跨整个视网膜深度的神经胶质样细胞)充当光导,提供无散射路径,将图像从内视网膜表面传输到受体而不会降解(Franze 等人,2007 年)。灵长类动物中央凹的情况以不同的方式解决:内视网膜的大部分神经材料被移到中央凹周边之外,而中心的受体在光学上不受阻碍。光感受器对光的吸收
光感受器通常又长又窄(人类视杆细胞的载有感光色素的外节长约 25 微米,宽约 1-2 微米,约含有 10 8 个视紫红质分子)。受体吸收的光比例取决于其长度。通常,由圆盘构成的脊椎动物光感受器每微米长度吸收约 3% 的入射光,而由微绒毛构成的无脊椎动物受体每微米吸收约 1%。要吸收 90% 到达它的光,脊椎动物受体需要长 77 微米,昆虫受体需要长 230 微米。这些数字对于这两组受体来说相当典型(人类视杆细胞相当短)。吸收率和受体长度之间的关系是对数的,而不是线性的,因为随着受体距离的增加,吸收率会降低s 光被吸收。如果光是单色的(这大致适用于只有蓝光穿透的深海),则长度为 L 的受体吸收的入射光的比例可以从
(1 − e –kL ) 中找到,对于白光,可以从 [ kL /(2.3 + kL )] 中找到,白光是陆地条件下的典型。k 是吸收系数——如果 L 以微米为单位测量,则为每微米吸收的光的比例。框 3.2 给出了一些与吸收相关的常见术语的定义。受体的长度也会影响其光谱灵敏度,这是“自我屏蔽”的结果。光路早期的色素吸收了接近最大灵敏度波长的大部分光,这意味着剩余的色素吸收了更多距离峰值较远的剩余光。这扩大了整个受体的光谱灵敏度。关于受体吸收的有用讨论,特别是它如何依赖于波长,可以在 Warrant 和 Nilsson (1995) 中找到。
61
分辨率和眼睛设计
现在,我们可以使用前面几节中概述的物理原理,得出一些关于眼睛大小和构造与其提供的分辨率之间关系的确切结论。一种令人满意的方法是尝试根据特定规格“设计”眼睛。如果可以做到这一点,使用这些原理,我们可以相当肯定没有遗漏任何重要的东西。
想象一只小型脊椎动物,它的单腔晶状体眼睛在设计上与我们的眼睛相似。这种动物是一种在明亮的日光下进食的食草动物(这避免了下一节将讨论的光子稀缺问题)。
它需要分辨 3 米处的草,从角度上讲,这近似于每度 10 个周期的光栅。将度数转换为弧度可得出
框 3.2 与吸收相关的术语
吸收或衰减描述的是光或其他形式的能量在穿过给定长度的物质时被吸收的程度(图 3.8):
kL
o
I I e− =
其中 I o
是入射强度,I 是通过长度 L 后的强度,k(吸收系数)是每单位长度吸收的光的比例:例如,对于脊椎动物的视杆细胞,每微米吸收 3%(0.03)。
透射率是透射光能与入射光能之比:
T = I / I o
,T 也等于 e −kL
与 T 相关的是吸收率,即吸收的能量分数,即 1− T ,
或 ( I o
– I ) / I o
吸光率或光密度是吸收的对数测量,
是透射率的负对数:
A I I 10 o
log (/ ) =−
使用吸光率的优点是它们可以相加,因此 0.2 和 0.4 的中性密度滤光片的组合具有 0.6 的光密度。
图 3.8 光穿过吸收介质的衰减(见正文)。
62 动物的眼睛
视网膜采样频率vs为10×57.3,即每弧度573个周期,根据公式(3.2),这意味着f/(2s)= 573。波导考虑意味着受体分离s不能小于约2μm(1μm受体和1μm间隔),因此焦距f必须至少为573×4μm,即2.29毫米。人们会期望视网膜采样频率与光学截止频率vco非常接近,就像人眼一样,一方面避免“未使用的”分辨率,另一方面避免多余的受体。因此,vco
也是每弧度 573 个周期,根据方程
(3.4),这意味着 D / λ = 573。如果 λ 为 0.5 μm,则眼睛的孔径 D 必须为 1.15 mm。因此,这只虚构的眼睛的主要特征——焦距、孔径和受体直径——都源于进化赋予它的任务,以及适用于眼睛的特定物理原理。
灵敏度
低光子数的后果
与小光子数相关的统计不确定性意味着,在低光照水平下,眼睛的潜在分辨率无法实现,如图 3.1 所示。 1941 年,Hecht、Schlaer 和 Pirenne 首次清晰地证明了人类视杆受体能够检测到单个光子,而 Pirenne 的著作《视觉与眼睛》(1967 年)中的图 3.9 就是基于这项研究。这四幅图均显示了视网膜上同一明亮区域的图像,其中包含一个黑色圆形斑块,但光照水平不同。在 I 中,光照水平非常低,以至于 400 个受体中只有 6 个接收到光子:这大约是人类视觉阈值的情况。(尽管单个受体能够检测到单个光子,但大脑需要大约 6 的“安全系数”,这样就不会对自发的视紫红质激活做出反应。)在 II 光照水平高出十倍,但暗斑仍然不可见,隐藏在光子撞击的随机背景“噪声”中。III 赌徒可能准备猜测视野中有一个黑暗区域,但只有 IV,即阈值水平的 1000 倍,暗斑才会确定地突出。这个证明清楚地说明了为什么我们在黑暗中看得这么差。在比图 3.9 所示的更高的光照水平下,可以区分不同深浅的灰度,最终可以区分微小的对比度,例如在接近分辨率极限的光栅图像中出现的对比度(图 3.3)。为了分辨这些光栅,检测百分之几的对比度的能力至关重要。需要多少光,或者更准确地说,每个受体需要多少光子才能检测到特定的对比度?这个问题最早由 Hugo deVries 和 Albert Rose 在 20 世纪 40 年代研究,他们得出的一般答案是,可检测的最小对比度与强度平方根的倒数成正比(Rose-deVries 定律)。在方框 3.3 中,我们将看到这条规则是如何从光子捕获的统计数据中产生的,然后讨论它对视觉的影响。令人印象深刻的是,方程 (3.5) 预测的一些光子数必须有多大。如果光栅中的对比度为 0.5(50%),则所需的数量为 1/0.5 2 = 4。对比度为 10% 时,数量为 100,但当对比度降至 1% 时,人类可以轻松检测到,数量为 10 000。这些数字指的是一次收集的光子。图 3.9 低光子数的影响。四个面板显示了人类视网膜中 400 个受体的正方形,其中光子捕获的样本分布在视觉阈值 (I) 和三个更高的光照水平,每个水平之间增加 10 倍 (II-IV)。中心的暗盘只有在强度为阈值的 100 到 1000 倍时才可靠地被检测到。来自 Pirenne (1967)。
I II
III IV
64 动物眼睛
框 3.3 检测给定对比度需要多少光子?必须确定的是,光栅中两个条纹之间的实际强度差异(在视网膜中表示为受体捕获的光子数量差异)是否大于“噪声”水平,即到达受体的光子数量的统计波动。幸运的是,在这种统计数据(泊松分布)中,噪声和信号大小密切相关。光子数的变化(以重复样本的标准偏差 σ ( n ) 来衡量)等于样本中平均数 n 的平方根,即 σ ( n ) = √ n。此属性在许多“嘈杂”过程中很常见,例如涉及少量电子的电阻电路中的电流波动。光栅中的对比度 ( C ) 先前定义为条纹对之间的强度差(Δ I = Imax
− Imin
)除以强度之和,即 C = Δ I / 2I ,其中 I 是平均强度。在单个样本对中,我们可以用光子数代替强度,从而得到 Δ n / 2n,其中 n 是平均光子数。要将亮度差异视为真实差异,普通统计推理表明,样本之间的差异 Δ n 应该大于标准差 σ ( n ),或者,在 95% 的确定性下,2 σ ( n )(如图 3.10 所示)。因此,如果 Δ n > 2 σ ( n ),则可以检测到差异。为了得到答案,我们需要对这个表达式做两件事:将两边除以 2n,并将 σ ( n ) 替换为 √ n。现在得到 Δ( n )/ 2n > 2 √ n /2 n。左侧平均等于 Δ I /2 I,
即对比度 C ,右侧则简化为 1/√ n。
因此最终结果是:
图 3.10 光子统计和对比度检测。该图显示了光子样本在对亮度略有不同的两个区域进行成像的受体中的分布方式。
如果光子数的平均差异 ( d n ) 大于每个分布标准偏差 ( s ( n ) ) 的两倍,则可以可靠地检测到亮度差异。
概率
dn
s(n)
平均光子数 ( n–)
框 3.3 检测给定对比度需要多少个光子? (续)
>
√
C n n C2
1/ ,或 1/
65
>
(
3. 5 )
第一个表达式是前面提到的 Rose-deVries 定律的一个版本
,第二个表达式告诉我们每个受体需要多少光子来检测特定的对比度。
1.0
对比度
0
νmax
νco
0
1.0
空间频率 (ν)
图 3.11 分辨率和对比度损失。低光子数限制了可检测的最小对比度。
这样做的效果是将对比度传递函数中的对比度设置为“下限值”(参见图 3.3),这反过来又将最大可检测空间频率 (vmax) 限制为截止频率 (vco) 的一小部分。在这种情况下,将最小对比度提高到 0.32 会将最大频率降低到亮光值的约 58%。眼睛的“积分时间”:粗略地说,这是受体对强度变化做出完全反应所需的时间,通常为 0.1 秒或更短。因此,在低对比度下,每个受体每秒需要大约 105 个光子。这仍然是低估了,因为出于各种原因,从场景到达眼睛的光子中只有一部分实际上被视紫红质分子吸收。在人类中,这个比例约为 10%,这意味着检测 1% 对比度所需的光子数量接近每个受体每秒一百万个。这是一个非常大的数字,显而易见的下一个问题是:“世界为我们提供了多少光子来观察?”。
可用光子数
白色卡片在明亮阳光下的辐射度(R)(它发射的光子数量的度量)约为 10 20 m –2 .sr –1 .s −1 ,在室内光线下约为 10 17 ,在月光下为 10 14 ,在星光下为 10 10 - 人类视觉的绝对阈值。 (单位的含义在第 2 章中解释。)这些数字看起来很大,但是从外部空间的平方米到以平方微米为单位的光感受器尺寸,它们会缩小 10 12 倍。同样,单个受体接受的光锥通常小于 1 平方度,而一个立体角(即 65.5° 直径的锥)有 3283 平方度,这又使光子数减少了 10 3 或更多。这将受体可用的最终数量减少到每秒一百万或更少,使它们进入光子数开始限制对比度检测的范围。这导致了一个非常重要的结论:除了明亮的日光外,眼睛在所有光照水平下都处于“光子匮乏”状态 - 即它们无法发挥其潜在能力。除了限制对比度检测之外,低光子数还会降低敏锐度。这最容易通过考虑对比度传递函数的变化来解释(图 3.11)。如果最低可检测对比度因光子数减少而增加,则相当于提高图表的基线,从而切断曲线的底部。因此,如果每个接收器每积分时间仅有 10 个光子,对比度极限将为 32%(根据公式 3.5),这将限制最大可检测空间频率为明亮光线下值的 0.6 以下,即截止频率。这基本上就是为什么精细工作需要高光照水平的原因。
使眼睛更敏感
从上述内容可以看出,眼睛捕捉到的光子越多越好。这在正常光照水平下很重要,但对于夜行动物(月光比阳光暗一百万倍)和生活在深海的动物来说,压力甚至更大,即使在最清澈的水中,每 70 米的光线也会减少 10 倍。我们可以将这种捕获光子的能力称为眼睛的灵敏度,并将其定义为当眼睛观看标准辐射度 (R) 的场景时,每个受体捕获的光子数量 (n)。眼睛的灵敏度主要由两个特征决定:瞳孔直径 D 和每个受体接受光线的空间角度 (Δρ)。目前,Δρ 由 d / f 给出,即受体直径在眼睛节点处形成的角度(见图 3.12)。受体长度也很重要,如前面“光受体光学”部分所述,此处添加了术语 P abs 以考虑进入受体并被感光色素吸收的光子比例(通常在 0.1 到 0.9 之间;参见上文“光受体光学”)。灵敏度 S 由下式给出:
该方程很容易从光度测定法中推导出来,Land (1981a) 给出了完整的解释。(0.62 的因子是 (π/4)2,这是因为孔径和接收器都具有圆形横截面。请注意,对于小角度,Δρ2 是立体角(以球面度为单位)。这里重要的是,实际上只有一个变量可以安全地改变以提高灵敏度,那就是孔径 D。增加 Δρ 也会增加灵敏度,但会以牺牲分辨率为代价,因为在单腔眼中,Δρ 和接收器间(采样)角度 Δφ 几乎相同(图 3.2)。
让我们看看,在实践中,眼睛如何变得更加敏感(图 3.12)。最初可以增加光圈:从日光直径变为2 毫米到 8 毫米(夜间),人类瞳孔可使眼睛的灵敏度提高 16 倍。对于夜行动物(如猫头鹰和负鼠),瞳孔几乎与眼睛本身一样宽。但显然,D 不能大于眼睛直径,因此最终一定是眼睛大小限制了灵敏度。任何进一步的灵敏度提高都需要更大的眼睛来容纳更大的瞳孔,事实上大多数夜行动物都有大眼睛。然而,增加眼睛尺寸,从而增加焦距 f,实际上会减少 Δρ,它由 d / f 给出,因此要获得更大眼睛的回报,受体必须相应地变宽。
Δρ
D
f
d
图 3.12 增加眼睛的灵敏度。可以首先通过将光圈 (D) 加宽到最大可能(中心)来提高左侧眼睛的灵敏度。此后,在不改变分辨率(恒定接受角∆ρ = d / f 弧度)的情况下增加光子捕获的唯一方法是同时增加所有三个参数(D、d 和 f)。
68 动物的眼睛
在脊椎动物的眼睛中,大眼睛中的受体本身并不是特别大。相反,往往会发生的情况是,小受体在视网膜神经节细胞水平上被分组为更大的单元,从而增加了有效受体直径(空间总和)。这种安排通常非常灵活,因此受体“池”的大小可以随光照水平而变化,从而可以在白天的高分辨率(较小的有效Δρ)和夜间的高灵敏度(较大的有效Δρ)之间进行权衡。另一种策略是在更长的时间内收集光子(时间总和)。与空间总和一样,它也有缺点,在这种情况下,由于“快门时间”延长,运动模糊度增加。然而,如果使用得当,空间和时间总和可以非常有效地增强方程 (3.6) 中总结的纯光学适应性。例如,据估计,在最佳总和下,蝗虫眼可以将其视觉范围扩展到比光学单独提供的光强度暗 100 000 倍的光强度(Warrant 1999)。即使不考虑空间和时间总和,通过改变方程 (3.6) 中的参数,不同眼睛获得的灵敏度范围也非常大。对于日光下的人眼(D = 2000 μm,
表 3.2 一些动物眼睛的敏感度(S)
名称 敏感度 光照 栖息地 参考
Cirolana(海洋等足动物) 4200 深海 1
Oplophorus(十足目虾) 3300 深海 2
Lampanyctus(灯笼鱼) 247 深海 3
Dinopis(鬼面蜘蛛) 101 夜行性 2*
Limulus(马蹄蟹) 83–317 沿海主要夜行性 1*
Ephestia(蛾) 38 夜行性/黄昏性 2*
Onitis aygulus(蜣螂) 31 夜行性/黄昏性 4*
Phronima(超科片足类) 38–120 中层水域 1
人类(外围杆池) 18 昼行性 2*
章鱼 9.7 沿海海底 5
扇贝(扇贝) 4.0 沿海海底 2*
蟾蜍(蟾蜍) 4.0 主要昼行性 6*
滨蟹(Leptograpsus) 0.5 昼行性 1*
蜣螂(Onitis ion) 0.35 昼行性 4*
工蜂 0.32 昼行性 2*
跳蛛(Phidippus) 0.04 昼行性 2*
人类(白天的中央凹) 0.01 昼行性 2*
原始数据参考:1. Land 和 Nilsson(1990);2. Land(1981a); 3. Warrant、Collin 和 Locket (2003)
(假设神经节细胞场为 25μm);4. McIntyre 和 Caveney (1998);5. Hanlon 和 Messenger (1996);6. Warrant
和 Nilsson (1998)。 * 使用 6 中给出的方法重新计算白光值。
对于五种深海物种(无 *),使用单色光公式 S = 0.62 D 2 ∆ ρ 2 (1 − e − kL);对于所有其他物种(*),使用白光公式 S = 0.62 D 2 ∆ ρ 2 (kL (2.3 + k L))。∆ ρ 是从 d/f(受体直径除以焦距)获得的。
69
Δρ = 1.2 10 -4 rad, P abs
= 0.31) S 为 0.01 μm 2 .sr,而另一个极端是深海等足类甲壳动物 Cirolana ( D = 150 μm, Δρ = 0.78 rad, P abs
=
0.51) 的 S 值为 4200 μm 2 .sr。如果双眼都看同一个场景,甲壳类动物每个受体将捕获 420 000 倍的光子,这个比率与日光和月光之间的百万倍差异相差不大,尽管远远低于人类可用视觉的总范围 (10 10 )。表 3.2 给出了一系列动物的灵敏度数据。总体而言,S 值与动物栖息地的光照条件非常吻合。日行动物和水面动物的 S 值往往低于 1,黄昏动物和中层水域动物的 S 值在 1-100 范围内,而夜行动物和深水动物的 S 值在 100 和 1 之间0 000。Warrant 和 McIntyre (1990) 给出了另一种灵敏度值选择,显示出相同的趋势。
结论
“好”眼睛可以定义为在各种照明条件下都能很好地分辨的眼睛,现在我们可以看到哪些解剖特征使这成为可能。第一点是,这样的眼睛必须足够大,原因有三。需要长焦距来获得较低的最小可分辨角度和较高的视网膜采样频率(方程 3.2);需要大光圈来减少衍射,从而确保较高的光学截止频率(方程 3.4);还需要大光圈来让足够的光线进入眼睛,以确保足够的光子数,从而在昏暗的光线下进行良好的对比度检测(方程 3.5 和 3.6)。较大的眼睛绝对尺寸有利于提高分辨率和灵敏度,因此,在所有需要良好视力的动物中发现大眼睛的进化趋势并不奇怪。人类、鹰和蜻蜓的眼睛很大,以便更好地分辨,而猫、猫头鹰和飞蛾则更多地利用眼睛大小来提高灵敏度。深海中的猎人既需要分辨率,又需要灵敏度,因此有时眼睛也很大,这并不奇怪。记录的最大眼睛是深海鱿鱼的眼睛,直径接近 30 厘米。相反,在白天工作的低视力眼睛宽度可能不到一毫米。昼行性和夜行性眼睛之间的差异主要在于孔径的大小和每个受体接受光的空间角度 (Δρ)。人眼的瞳孔相对较小,F 值(摄影中的 f / D)在白天为 8,在晚上为 2。昼行性昆虫(例如蜜蜂)的 F 值通常约为 2。鱼类和夜行性陆生脊椎动物的 F 值更接近 1,而飞蛾和龙虾等某些节肢动物的 F 值可低至 0.5。由于图像亮度随(1 / F 值)2 变化,这意味着龙虾眼在夜间的光学性能是人眼在白天的 256 倍。对于昼行性眼睛来说,拥有大于防止衍射限制图像质量所需的瞳孔没有任何好处。事实上,这有缺点,因为其他缺陷(例如球面像差和色差)会变得更糟。但在黑暗中,高分辨率变得不可用,而对光子的需求至关重要,这就要求光圈应尽可能大。在日光下,光子充足,受体越窄越好,因为这意味着眼睛在给定分辨率下可以具有较短的焦距(方程 3.2),因此物理上较小。由于波导光学器件规定受体直径的下限约为 1 μm(图 3.7),这意味着焦距也不能变得非常小。因此,无论光线多么明亮,眼睛都必须具有最小尺寸。在黑暗中,更宽的受体更受欢迎,因为这会增加它们捕获光子的角度(Δρ)。这意味着,如果灵敏度增加,则固定尺寸的眼睛的分辨率理论上会降低。然而,在昏暗的条件下,精细分辨率无论如何都无法使用(图 3.11),因此分辨率和灵敏度之间的折衷有利于更宽的受体。受体直径似乎有一个实际的上限,约为 25 μm;龙虾和一些其他甲壳类动物就是如此。与人类中央凹的 2.5 μm 锥体相比,此类受体将接受 100 倍以上的光子。巧妙地处理分辨率和灵敏度之间的这种权衡,以便眼睛在不同光照水平下具有最佳分辨率,方法是使用较小的受体,但在较暗的条件下将它们集中到更大的集合中。有大量证据表明,脊椎动物和一些节肢动物的眼睛中就是这种情况。摘要
1.
眼睛的特征在于其分辨率和灵敏度。分辨率
是从角度角度上对光学环境进行采样的精细度。灵敏度可以量化为眼睛在观看标准亮度场景时受体接收的光子数量。
2. 分辨率取决于视网膜受体的采样密度,也取决于光学图像的质量。这种质量可能受到聚焦缺陷以及球面像差和色差的影响。它最终受到衍射(图像中光波的干涉)的限制。眼睛的孔径越大,衍射效应越小。
3. 由于波导效应,光感受器不能做得比 1-2 μm 更窄,否则会降低分辨率。 这意味着只有通过增加光学系统的焦距才能提高分辨率。
4. 在 d在光照下,检测对比度的能力受到受体可获得的光子数量的限制。捕获的光子数量越少,图像的统计质量就越差。通过使用高相对孔径(孔径直径/焦距)和宽受体,高灵敏度眼睛的光子数量最大化。但是,更宽的受体会损害分辨率。
t
5. 通常,分辨率的提高或灵敏度的提高都需要增加眼睛的尺寸。
这个页面用来放一些有关动物的视觉系统的进化的有趣知识。
视觉的基本分子机器:视蛋白opsin
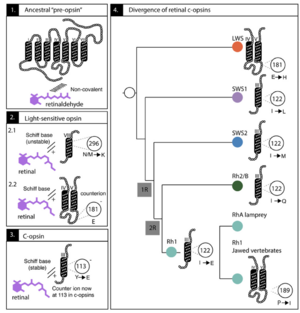
视蛋白(opsin)是一种G蛋白偶联受体,脊椎动物的c-opsin演化步骤大致如下:[1]
- 在扁盘动物门分化之前,就已经与视黄醛非共价结合
- 在刺胞动物门分化之前,296号残基从天冬酰胺/甲硫氨酸突变为赖氨酸,得以共价结合;181号突变为谷氨酸,稳定了席夫碱
- 在后口动物的共同祖先中,113号残基从酪氨酸突变为谷氨酸,代替了181号谷氨酸的功能。这使得181号谷氨酸不再受到巨大的选择压力而可以变为其他的残基,这有时有助于改变最适波长。
- 在脊椎动物的共同祖先中,一种视蛋白分化为多种。
感受光的细胞:杆状Rhabdomeric 和纤毛状Ciliary
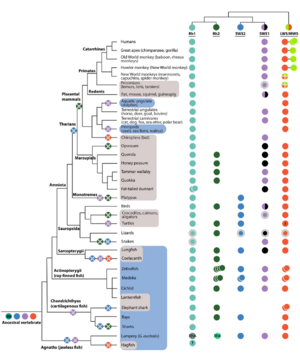
动物的含有视蛋白的感光细胞可以分为两类:一类是杆状感光细胞(rhabdomeric photoreceptor cell),一类是睫状感光细胞(ciliary photoreceptor cell)。[2]
Animal eyes 第二版
- ↑ The evolutionary history and spectral tuning of vertebrate visual opsins,https://doi.org/10.1016/j.ydbio.2022.10.014
- ↑ 此皆“术语在线”上生物物理名词上给出的译名,个人认为,睫状感光细胞是匪夷所思的误译。“ciliary”,纤毛的,描述的是这类感光细胞感光部分来自于其纤毛,而睫状肌“ciliary musucal”的ciliary描述的是其于眼球附近结构相关。换言之,ciliary photoreceptor cell 应该译为“纤毛状感光细胞”,和睫状体没有关系。造成误会的原因是纤毛的名称来自于“睫毛”,而睫状体类似。 参考:ciliary 一词起源于 1685-1695 年左右。 cilia 纤毛一词起源于几年后的 1705-1715 年,是 cilium 的新拉丁语复数形式,cilium 意思是睫毛。在拉丁语中,cilia 的意思是上眼睑,可能是 supercilium 的逆成词,supercilium 是眉毛。后缀 -ary 最初出现在中古英语 (-arie)、古法语 (-er, -eer, -ier, -aire, -er) 和拉丁语 (-ārius) 的外来词中;它通常可以表示“与、与”、“贡献”和“为了”。综上所述,cili(a)-ary 与眼睛内部和周围的各种解剖结构有关,即睫状体和眼睛晶状体的环状悬吊。
