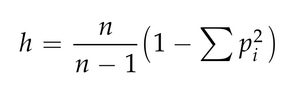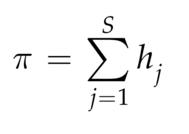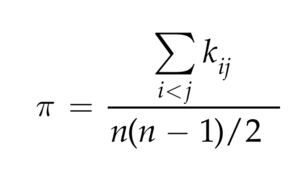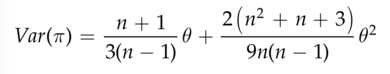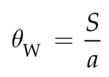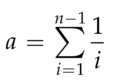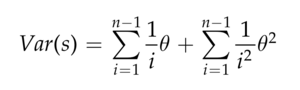第三章 描述变异
一旦我们从感兴趣的种群中获得序列样本,我们就必须描述观察到的变异。有很多方法可以总结单个核苷酸、微卫星和完整序列的分子变异,因此有很多不同的统计数据来描述数据。统计数据只是观察样本(序列)的总结。在分子群体遗传学中,我们倾向于关注那些作为理论参数 θ (≡4Neμ) 估计量的统计数据,它表示在假设种群中常染色体基因座处发现的变异量,其中所有变异都是中性的,并且处于突变漂移平衡状态。这种关注的动机是希望将我们的经验观察与中性模型的理论预测联系起来,该模型既包括自然界中发现的多样性数量,也包括具有不同 θ 值的种群中选定突变的预期动态。然而,值得注意的是,下面讨论的统计数据只是在相对严格的假设下对 θ 的估计——即理想化的无选择种群和人口平衡,以及每个突变模型特有的额外限制。还有其他方法可以理解这些统计数据,在本章后面,我将讨论对变异摘要的几种不同解释。
还有越来越多的最大似然 (ML) 和贝叶斯方法可用于从数据中估计参数 θ(例如,Kuhner、Yamato 和 Felsenstein 1995;Nielsen 2000;Beerli 2006)。一些基于似然的方法甚至可以从预先确定的 SNP 面板而不是完整序列数据中估计 θ,只要确定方案是精确已知的(例如,Kuhner 等人 2000)。虽然这些方法越来越受欢迎,并且比基于矩的估计器具有一些优势,但它们也有一些重要的局限性。这些限制大多是计算上的:可以分析的数据集的大小(就样本数量和序列长度而言)是有限的。这些方法不能扩展到全基因组(甚至整个染色体)数据集。此外,许多基于可能性的方法(ML 和贝叶斯)在处理缺失数据时效果不佳,这一限制尤其适用于可能对核苷酸具有可变覆盖范围的全基因组重测序项目。随着计算工具和资源的改进,许多这些问题将被克服,但在这里我将仅讨论一些最常用的从简单数据摘要中总结序列多样性的方法。
序列多样性测量
无限位点模型下 SNP 的 θ 的常用估计量
对于单个核苷酸多态性,某个位点的第 i 个等位基因的样本频率为 pi,因此所有等位基因频率之和等于 1。如果我们只考虑双等位基因位点,那么显然 p1+p2 = 1。总结单个多态性位点变异的一个有用方法是计算样本杂合性,其公式如下:
其中 n 是样本中的序列数。虽然这个值可以根据从杂交个体、近交系或单倍体染色体获得的数据计算出来,但它被称为杂合性heterozygosity(或更确切地说,预期杂合性 expected heterozygosity),因为它是如果配子随机结合(即,如果染色体随机配对以产生二倍体个体),则所有个体中杂合子的比例的估计值。事实上,无论数据来源如何,通常将许多核苷酸多样性测量称为杂合性测量。
鉴于单个位点的多样性测量,我们现在考虑整个序列的多样性测量。有两种方法最常用于总结核苷酸多样性,因为它们不需要分配衍生和祖先等位基因(使用此信息的其他测量如下所述)。根据我们上面对单个位点杂合性的定义,我们可以将位点杂合性的总和定义为:

其中 S 是分离位点的数量,hj是第 j 个分离位点的杂合性,如公式 3.1 中定义的那样(Nei 和 Li 1979;Nei 和 Tajima 1981a;Tajima 1983)。在平衡状态下的二倍体 Wright-Fisher 种群的无限位点模型下,E(π) = θ,这就是为什么这个统计数据有时被称为 θπ。作为参数估计量的统计数据通常用上面的插入符号表示,但我不会在这里使用这种符号。因为单态位点的杂合性为 0,所以我们也可以对比对中的所有位点求和,而结果没有变化。计算图 1.1 中所示的比对的 π,我们发现六个多态性的位点杂合度分别为 0.5、0.667、0.5、0.667、0.5 和 0.5,得出 π = 3.33。我们经常给出的是每个位点的平均值,在这种情况下π = 3.33/15 = 0.222。
这个多样性度量给出了任意两个序列之间成对核苷酸差异的平均数量,因此也可以计算为:
kij是样本中第i个和第j个序列之间的核苷酸差异数量,分母表示n个序列之间进行的唯一比较的数量。如果我们要计算图1.1中四个序列的六个可能的成对比较中的每一个的差异数量,我们会再次发现平均差异数量为3.33。如果序列数量很大,使用公式3.2计算π比使用公式3.3计算π要有效得多。
正如本书前面所讨论的,我们在计算序列之间的差异时经常忽略插入/缺失变异。当应用公式 3.2 时,具有插入/缺失的单个序列被视为缺失数据,因此在计算位点杂合性时,n 的值在不同位置会有所不同。在对具有不同覆盖范围(因此有大量缺失数据)的数据集进行重新测序时,情况也是如此。当应用公式 3.3 时,通常只是忽略 n 个序列中任何具有间隙字符的比对位置。这种方法将对公式 3.2 和 3.3 产生的 π 计算产生影响,正如我们可以使用图 3.1 中所示的修改后的比对所证明的那样。
在这种情况下,使用公式 3.2 可得出 π = 3.49(第一个分离位点的 h = 0.66 而不是 0.5),但使用公式 3.3 可得出 π = 2.83,因为我们已将位置 1、2、9 和 10 完全排除在所有成对比较之外。即使在有间隙的位置内没有分离位点(如图 3.1 中的第二个位点所示),不同的方法在按每个碱基对计算时也会得出不同的结果。这是因为第一次计算包括了所有 15 个位点,但第二次计算仅包括了 11 个位点。尤其是对于基因组规模的数据集,应用可以轻松处理大量缺失数据的方法(例如基于公式 3.2 的方法)会更加有用(例如,Begun 等人,2007 年;Ferretti、Raineri 和 Ramos-Onsins,2012 年)。
我们还可以将 π 中的预期方差量表示为参数 θ 的函数。我们根据理论模型来表示方差,因为我们知道样本中的变异结构有很大的历史成分——即与采样染色体相关的谱系结构。尽管中性平衡模型下 π 的理论方差并不总是理想的(例如,在种群不符合我们的假设的情况下),但另一种方法是使用非常不准确的预期,这些预期不考虑底层谱系的层次结构,并且远低于大多数数据集中观察到的值。对于无重组的情况,此理想模型下π的预期方差为:
如公式 3.4 所示,π 存在大量方差,即使有大量样本,方差也不会接近于零(Tajima 1983)。Pluzhnikov 和 Donnelly (1996) 给出了位点内重组水平增加时的预期方差。
π 的另一种总结核苷酸变异的方法是使用样本中分离位点的总数 S。但是,由于样本量越大,S 的值也越大,因此我们必须将统计量调整为(Ewens 1974;Watterson 1975):
其中 a 等于:
统计量通常称为 Watterson 的 theta,因为它也是假设 Wright-Fisher 群体处于平衡状态和无限位点突变模型时参数 θ 的估计量。我们还可以重写上述方程,以将预期的分离位点数表示为 θ 的函数:E(S) = θa。给定图 1.1 中的序列比对,θW = 6/(1/1 + 1/2 + 1/3) = 3.28。我们可以看到,这个值与 π 给出的值非常相似。再次,θW 的确切值可能会在有间隙的比对中出现差异,这取决于我们是否包括或排除有间隙的位置。如果我们包括有间隙的位置,我们需要为具有不同序列数的区域计算单独的 θW 值,因此对于具有四个序列的位置,θW = 5/(1/1 + 1/2 + 1/3) = 2.73,对于图 3.1 中具有三个序列的位置,θW = 1/(1/1 + 1/2) = 0.667。统计量的总值是这两个的总和,θW = 3.40,并且每个站点的测量必须相应地对具有不同样本数的位置数进行加权。
我们可以再次给出 S 的预期方差s θ,假设 Wright-Fisher 种群处于平衡状态,无限位点突变模型没有重组:
当存在自由重组时,方差减少到公式 3.7 中的第一个项,因为不再存在任何进化方差(参见第 6 章)。Pluzhnikov 和 Donnelly (1996) 给出了中等水平重组的 S 方差。公式 3.7 还可用于查找预期方差,该方差由 Var (θW) = Var(S)/a2 给出,其中 a 的定义如公式 3.6 所示。
比较我们两个 θ 估计量的预期方差,我们发现 θW 的方差低于 π 的方差,并且随着样本量增大而趋近于零(尽管非常缓慢)。这似乎表明 θW 是两个估计量中“更好”的。然而,它对轻微有害等位基因的存在和测序错误也更为敏感,即使在平衡种群中也是如此(见下文)。因此,通常会同时使用这两个统计数据,以及对两者进行比较(即 Tajima's D 统计量;见第 8 章)。
等位基因的频谱
到目前为止,我们只考虑了使用单个汇总统计量(如 π 或 θW)来描述变异。但是,也有有用的图形方法来描述变异,而这些方法反过来又会引导我们更多地测量核苷酸多样性。考虑图 3.2A 中所示的比对。在这 10 条染色体中有 9 个分离位点,每个位点的频率在 1/n 和 (n − 1)/n 之间(请记住,如果一个等位基因存在于所有 n 条染色体上,则它不是多态性的)。如果我们不知道哪个等位基因是祖先的,哪个是衍生的,那么描述每个位点变异的一种简单方法是次要等位基因频率 (MAF),即不太常见的等位基因的频率。因此,样本中的次要等位基因频率范围为 1/n 到 0.5。我们可以通过绘制等位基因频率谱来直观地总结样本中所有分离位点的 MAF,其中直方图中的每个箱体代表与给定次要等位基因频率比对中的位点数(或位点比例)(图 3.2B)。如果我们将 Si
* 定义为在 i 条染色体上发现等位基因的分离位点的数量,其中 * 指定此计数与祖先/派生关系无关,并允许 i 的值在 1 到 n/2 之间(奇数 n 向下舍入),则等位基因频谱只是 Si 各种值的图
1 2 3 4 5 6 7 8 91011121314151617181920212223242526272829
GCTCACCGGAATTATCCGATATGCTAGTA
GCTTACCGGAATTATGCGATATGCTTGTA
GCTCACCGGAATTATGCGATATGGTAGAA
GCTCACCGGAATTATGCGATATGGTAGAA
GCTCACCGGGATGATGCGATATGCTAGTA
GCTCACCGGAATTATGCGATATGCTAGAA
GCTTACCGGAATTATCCGATATGCTAGTA
GCTCACAGGGATTATGCGCTATGCTAGTA
GCTCACCGGAATTATGCGATATGGTAGAA
GCTCACCGGAATTATCCGATATGCTAGTA
分离位点数
次要等位基因频率
图 3.2 (A) 对于每个分离位点,次要等位基因为蓝色,主要等位基因为黑色。对于此样本,n = 10、L = 29 和 S = 9。(b) (A) 中显示的比对的“折叠”等位基因频谱。等位基因频谱也称为位点频谱 (SFS),当它仅显示次要等位基因频率时,它被称为折叠频谱。为了推断每个等位基因的祖先和衍生状态,通常使用一个或多个密切相关物种的序列。通常认为与这些物种匹配的等位基因代表祖先状态,尽管每个谱系中的平行突变都可能导致错误的推论;这就是为什么通常首选使用两个外群物种的原因——所有三个谱系中平行突变的机会应该非常小。如果外群物种序列与任一等位基因都不匹配,或者它们相互矛盾,则无法将状态指定为祖先和衍生状态。图 3.3A 显示与图 3.2A 相同的比对,但一个等位基因已被指定为衍生状态。我们现在可以使用衍生等位基因频率 (DAF) 描述每个位点的变异,它可以介于 1/n 和 (n − 1)/n 之间。再次,我们通过等位基因频谱总结所有分离位点的 DAF,这次是在展开状态下(图 3.3B)。如果我们 是 i 条染色体上发现的具有衍生等位基因的分离位点的数量(i 现在从 1 到 n − 1),那么等位基因频率谱只是 Si 各种值的图。为了清楚起见,我只绘制了 Si,但通常也会将等位基因频率谱绘制为 Si /S,或每个频率下所有分离位点的比例(有关这一点的进一步讨论,请参阅第 6 章)。还应该清楚的是,一些 MAF < 0.05 的等位基因实际上可能具有 DAF > 0.95,因为如果不分配衍生值,就无法进行区分nd 祖先状态。这意味着忽略 MAF < 0.05 的位点(如果这些位点被认为是测序错误或有害突变,则可能会这样做)可能会导致进化上重要的变异的丢失。除了可以很好地总结变异之外,在后面的章节中,我们还将看到理论
1 2 3 4 5 6 7 8 91011121314151617181920212223242526272829
GCTCACCGGAATTATCCGATATGCTAGTA
GCTTACCGGAATTATGCGATATGCTTGTA
GCTCACCGGAATTATGCGATATGGTAGAA
GCTCACCGGAATTATGCGATATGGTAGAA
GCTCACCGGGATGATGCGATATGCTAGTA
GCTCACCGGAATTATGCGATATGCTAGAA
GCTTACCGGAATTATCCGATATGCTAGTA
GCTCACAGGGATTATGCGCTATGCTAGTA
GCTCACCGGAATTATGCGATATGGTAGAA
GCTCACCGGAATTATCCGATATGCTAGTA
GCTCACAGGGATTATGCGCTATGCTAGTA
GCTCACCGGAATTATGCGATATGGTAGAA
GCTCACCGGAATTATCCGATATGCTAGTA
数量分离位点
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0
衍生等位基因频率
图 3.3 与图 3.2 中的比对相同,但现在等位基因极化为
祖先和衍生。 (A) 对于每个分离位点,衍生等位基因为蓝色。 (b)
(A) 中显示的比对的“展开”等位基因频谱。
描述变异
关于等位基因频谱形状的预测可用于
推断一组序列的历史。
我们现在考虑几个总结序列多样性的统计数据,
这些统计数据使用有关衍生等位基因频率的信息,因为这些统计数据可以捕获有关我们数据的更多信息。 Fu 和 Li (1993a) 定义了一个统计量 ξ1
,基于样本中衍生的单例数,可以用本文使用的术语写成:
是仅在一条染色体上发现的具有衍生等位基因的分离位点数。该统计量有时称为 θe
(其中 e 指系谱的外部分支)。从图 3.3A 中的比对,我们可以计算出 ξ1
= 4 的值。我们无法从图 3.1 或 3.2A 计算出 ξ1
,因为我们没有识别衍生等位基因。但是,我们也可以根据样本中的所有单例(无论它们是祖先的还是衍生的)定义一个统计量,用本文使用的术语写成:
η = − (3.9)
* 如上所述(Fu 和 Li 1993a)。从图 3.2A 中的比对结果可知,η1 的值 = 3.6。(n – 1)/n 项可纠正以下事实:无论祖先/衍生关系如何,对样本中的所有单身人士进行计数,往往会略微多算中性平衡群体中预期的衍生单身人士数量。
使用祖先状态信息的第二个多样性汇总统计数据是 θH,它再次是 i 染色体携带衍生等位基因的分离位点的数量(Fay 和 Wu 2000)。 (根据 Justin Fay 的说法,θH
中的 H 指的是该度量赋予高频衍生等位基因或衍生变体纯合性的权重。)从图 3.3A 中的比对中,θH
的值可以计算为 ([12 * 4] + [22 * 1] + [32 * 2] +
[42 * 1] + [82 * 1])/45 = 2.36。我们可以看到,由于
所有这些统计数据 — ξ1
— 都是在无限位点突变模型下处于平衡状态的 Wright-Fisher 群体中 θ 的估计值;具体而言,E(ξ1
) = θ。这些关系的出现是因为我们知道在标准中性假设下等位基因频率分布的预期形状(见公式 6.8 和图 6.5)。了解预期频谱和该频谱的汇总统计数据对于检测自然选择(第 8 章)和非平衡人口历史(第 9 章)特别有用。
顺便说一句,我们还可以根据派生的等位基因频率定义 θW
和 π,如下所示:
其中 a 定义如公式 3.6 所示,并且:
图 3.3A 中对齐的 θW
和 π 值分别为 3.18 和 2.98。有关 θ 估计量之间差异的进一步讨论,请参见第 8 章。有限位点模型下 SNP 的 θ 估计量和包含测序误差 上述统计数据仅在几个限制性假设下才为种群突变参数 θ 的估计量。其中一个假设是,给定位点的突变仅发生过一次 — 即无限位点突变模型(第 1 章)。如果某个位点有多个突变,很容易看出这些统计数据为什么会向下偏差。例如,当多态性位点不是双等位基因时,统计量低估了多样性。在这种情况下,分离位点的总数小于单独突变的数量,因此 θW 低估了样本的杂合性。在多样性较低的种群中,这不会成为太大的问题:在人类样本中,三等位基因位点相对较少,而四等位基因位点几乎没有(Hodgkinson 和 Eyre-Walker 2010)。然而,在多样性较高的物种中,这可能是一个真正的问题(例如,Wang 等人,2010)。相反,在存在测序错误的情况下,这些估计值将向上偏差。这是因为错误会被误认为是真正的分离位点,因此许多这些位点将被纳入多样性统计的计算中。测序错误注定会成为基因组规模数据集中的一个大问题,这仅仅是因为大多数下一代测序技术更容易出错,而且许多位点在单个样本中的测序覆盖率较低,导致碱基调用不正确。
在这两种情况下——单个位置的多个真实突变或高测序错误——统计量 θW 会比 π 受到更大的影响(Tajima 1996;Achaz 2008;Johnson and Slatkin 2008)。在有限位点的情况下,π 的影响较小,因为位点上的第三(或第四)等位基因由于其频率较低,对成对差异的贡献较小。同样,我们预计测序错误只存在于一条或几条采样染色体上,因此这些错误对染色体间差异的平均数量影响很小。尽管如此,上述所有统计数据都会在一定程度上受到这些复杂因素的影响(Clark 和 Whittam 1992;Tajima 1996;Achaz 2008;Johnson 和 Slatkin 2008;Knudsen 和 Miyamoto 2009)。Tajima(1996)提供了多种方法来调整 θW 的计算,以通过使用 Jukes-Cantor 校正(第 7 章)并假设没有测序错误来解释有限位点突变模型。要调整 θW
需要计算样本中的最小突变数 S′,而不是分离位点数 S。如果我们的样本中某个位点有 j 个不同的等位基因,则该位点至少发生了 j − 1 个突变;将比对中所有位置的 j − 1 值相加可得出 S′。 (请注意,如果所有位点
都是双等位基因,则 S′ = S。)使用每个位点的突变数(即除以序列长度 L),Tajima 表明,考虑到位点发生多个突变的可能性,sta 的新版本为:
( / ) W(finite)
− ′ (3.13)
其中 a 定义见公式 3.6,b 定义为:
=
对于图 3.2A 或 3.3A 中所示的比对,S′ = S = 9 和 θW(finite)
在整个基因座上等于 0.125 * 29 = 3.62(与 θW 相比)
同样,使用 Jukes-Cantor 校正考虑位点发生多个突变的可能性的 π 的新版本为公式为:
1 4( / )/3 有限
π = − (3.15)
其中 π 根据公式 3.2 或 3.3 计算(Tajima 1996)。对于图 3.2A 或 3.3A 中所示的比对,π/L = 2.98/29 = 0.103。按照公式 3.15,π有限
= 0.119,整个基因座等于 3.45。
我们可以看到,校正了位点发生多个突变的可能性后,两个统计数据的值都略大于未校正版本,这与我们的直觉一致,即忽略有限位点的效果是低估核苷酸多样性。
使用任何测序技术都会发生测序错误,从传统的基于 Sanger 的方法到现代的下一代方法。如第 2 章所述,研究人员可以采取一些措施来最大限度地减少错误,包括在进行 Sanger 测序时对多个克隆进行测序,以及在使用下一代技术时使用严格的过滤器(包括最小读取深度和最低质量得分)。但是,增加最低可接受质量得分或读取深度也会导致偏差:随着越来越多的真实多态性被消除,估计的杂合性水平将不可避免地下降(Lynch 2008)。相反,大多数对 θ 估计量误差的修正都利用了这样一个事实,即错误很可能只会在单个染色体上发现,因此会在样本中显示为衍生的单例(Achaz 2008;Johnson 和 Slatkin 2008;Knudsen 和 Miyamoto 2009)。其他方法基于对单个杂交个体的深度测序,并且在具有两个以上等位基因的位点处识别出错误(Lynch 2008)。由于我们不知道较大样本中哪些单例是错误,因此我们必须忽略所有单例,在去除预期单例数量后调整使用预期分离位点数量(θW)和成对差异(π)的统计数据(仅基于样本中单例数量的统计数据显然无法以这种方式进行校正)。已经提出了多种方法来执行这种或类似的校正(例如,Achaz 2008;Johnson 和 Slatkin 2008;Knudsen 和 Miyamoto 2009),但在这里我仅介绍 Achaz(2008)中给出的误差校正估计量。让我们将 Smulti 定义为非单例(多例)分离位点的数量,即不包括衍生单例的分离位点的数量:Smulti。现在我们可以引入一个基于 Smulti 的新统计数据,以充分纠正测序错误:θ = − (3.16),其中 a 如公式 3.6 中定义。使用 t图 3.3A 中显示的比对,
= 2.73(相比于同一数据集的 θW
= 3.18)。
类似地,如果我们将 πmulti
定义为仅针对那些没有派生单例的多态性位点的位点杂合度之和(公式 3.2),那么我们可以给出另一个考虑误差的新统计数据:
使用图 3.3A 中显示的比对,θπ(multi)
= 2.72(相比于同一数据集的
π = 2.98)。Achaz (2008) 还展示了如果不知道派生状态和祖先状态,如何校正 θW
π 的错误。
θW(multi) 和 θπ(multi) 都将准确估计无限位点突变模型下 Wright-Fisher 群体平衡状态下的参数 θ,假设所有错误都以单例形式存在于样本中。由于测序技术存在一致的偏差,多条染色体上存在的错误不会被这种方法所解释。
无论标准中性模型的假设是否正确,θW(multi) 和 θπ(multi) 都表示总结核苷酸多样性的统计数据,而不计算衍生的单例,因此在错误率高时可能是首选。请注意,虽然我们对有限位点和测序错误的修正都是标准 θW 和 π 的特殊情况,但它们对突变过程的假设非常不同。有限位点的校正明确允许一个位置有三个等位基因,但没有错误,而校正测序错误的框架假设存在无限个位点,因此没有多个命中不是错误的位置。最后,虽然我们之前看到θW的理论方差低于π,但这个预期假设没有测序错误。在存在测序错误的情况下,π成为一个“更好”的多样性度量,因为它受这些错误的影响较小(Achaz 2008;Johnson and Slatkin 2008)。当然,这两个统计数据都比仅使用单例(ξ1)的估计器更稳健,因为这些估计值预计受测序错误的影响最大。解释核苷酸变异的测量值
在中性模型下(分离位点的所有等位基因都是选择性等价的,并且选择对与中性变异相关的位点没有影响),基因座的变异水平仅受突变输入与遗传漂变导致的等位基因丢失之间的平衡控制。如果这些假设成立,并且种群处于平衡状态(甚至在不平衡时也经常如此),则每个位点序列之间核苷酸差异的预期平均数π为(Li 1977;Tajima 1983):
在这种情况下,基因座的多态性水平应与有效种群大小(决定遗传漂变的影响)和中性突变率成线性比例。
然而,多样性与表观种群大小的相关性很弱。这种早期的观察结果被称为变异悖论(Lewontin 1974),即使在收集了更多数据集之后,这种悖论仍然存在(Leffler 等人 2012;Corbett-Detig、Hartl 和 Sackton 2015)。对生命之树上数百个物种的核苷酸变异的测量继续表明,尽管种群大小相差许多数量级(从普遍存在的细菌到极其稀有的脊椎动物),但细菌和脊椎动物之间核苷酸多样性的平均差异不到两个数量级(图 3.4)。在真核生物中,线粒体 DNA 的变异水平与种群大小没有相关性(Bazin、Glemin 和 Galtier 2006),核基因与我们假设的不同生物的普查种群大小之间只有微弱的关系(图 3.4)。除了假定的种群规模和变异水平之间缺乏线性关系外,重组率和变异水平之间存在意外的正相关性(Hahn 2008;Cutter 和 Payseur 2013 进行了综述)。在中性模型下,这种相关性是意料之外的,但在包含连锁选择效应的模型下,这种相关性是意料之中的(见第 1 章和第 8 章)。两个最完整的连锁选择模型预测多样性和种群规模之间存在弱正相关关系(背景选择;Charlesworth、Morgan 和 Charlesworth 1993)或无关系(搭便车;Maynard Smith 和 Haigh 1974),并且都预测重组率和变异水平之间存在正相关关系。背景选择模型提出,必须从种群中去除的有害突变的不断涌入会降低链接位点的多态性。搭便车模型认为,有利等位基因的快速固定会降低链接位点的多态性。虽然区分这两种模型并不简单(Stephan 2010;Coop 和 Ralph 2012),但我们可以写下两种模型下每个位点序列之间预期的平均核苷酸差异数。
在背景选择模型下,π 的期望值为:
其中 f 是种群中不携带有害突变的同源染色体的比例(Charlesworth、Morgan 和 Charlesworth 1993)。无突变染色体的比例取决于有效种群大小和重组率,以相对复杂的方式取决于对显性、重组和突变的假设(Charlesworth、Morgan 和 Charlesworth 1993)。但很容易看出,随着重组率的降低,具有中性多态性的位点将越来越多地与邻近的有害等位基因相连,导致 f 降低,π 随之降低。在具有重组的搭便车模型下,每个位点序列之间预期的平均核苷酸差异数的一个表达式是:其中 ρ = 4Ne c(群体重组参数;参见第 4 章),α 是一个复杂参数,取决于有利等位基因出现的速率、群体尺度的选择强度(Ne s)以及所选等位基因与正在分析的中性多态性的距离(Wiehe 和 Stephan 1993)。可以看出,重组水平的提高导致多样性水平非常接近没有选择的预期。增加搭便车效应(即增加 α)会降低多样性水平。不同搭便车模型的细节对 π 的期望略有不同,但重组水平和多样性之间几乎总是存在正相关关系。这些考虑意味着,虽然根据定义 θ = 4Ne
μ,但统计数据 π、θW
不一定等于 4Ne,尽管它们是无限站点模型下 Wright-Fisher 群体中 θ 的无偏估计量。在存在连锁选择的情况下——即使在正常重组区域也会产生重大影响(例如,Loewe 和 Charlesworth 2007),用于测量多态性水平的统计数据将至少告诉我们有关自然选择对连锁变异(遗传草案;Gillespie 2000)的随机影响,就像它们将告诉我们有关漂移和突变的影响一样多。这也意味着,通过将 π 除以 4μ 计算的有效种群大小 (Ne) 的值可能无法表示可解释的生物学值(当然也不是“个体”的数量;第 1 章),因为它仅代表中性模型下的有效种群大小。该数量的合并有效种群大小定义可能仍然代表合并的时间尺度,但 Ne 值的重新缩放将无法捕捉连锁选择模型的所有方面(Neher 2013)。相反,π 与表观普查种群规模有相关性(尽管相关性很弱)(图 3.4)这一观察结果表明,直接使用这种或其他核苷酸变异总结可能与使用不适当的 Ne 估计值一样有效。此外,普查种群规模在确定适应率方面可能比任何有效种群规模都更重要,因为普查种群规模在确定适应性突变的输入率方面发挥着重要作用(例如,Karasov、Messer 和 Petrov 2010)。选择性环境变化的速度也可能比任何种群规模概念在适应性进化中发挥更大的作用(Gillespie 2001;Lourenço、Glémin 和 Galtier 2013)。多样性的其他测量方法
微卫星变异
单个微卫星位点的变异可以采用与单个核苷酸位点变异大致相同的方式进行测量,尽管通常存在远多于两个等位基因(通常 >10 个等位基因)。这些等位基因在重复长度方面也会有很大差异,单个等位基因的重复单元数从 1 到 >30,具体取决于微卫星的结构。变异不必围绕平均重复长度呈正态分布,事实上,变异通常是双峰或甚至三峰的(参见图 3.5 中的示例)。
有多种方法可以总结微卫星位点的多样性,包括基于简单汇总统计数据的方法(见下文)和基于最大似然的方法(例如,Nielsen 1997;Wilson 和 Balding 1998;RoyChoudhury 和 Stephens 2007)。与总结核苷酸变异一样,最常用的统计数据也是 Wright-Fisher 平衡种群中种群突变参数 θ 的估计值m。
在这种情况下,突变率 μ 测量微卫星位点上新中性等位基因的突变率,我们必须假设一个适合微卫星的突变模型。最常用的模型是逐步突变模型 (SMM),它只允许每个突变发生单个重复单元变化(第 1 章)。
总结微卫星位点变异的一种直接方法是报告样本中不同等位基因的数量 K(有时表示为 )。虽然该统计数据可用作 θ 的估计量(例如,Haasl 和
等位基因大小
等位基因大小
图 3.5 人类微卫星位点等位基因变异示例。两个位点
都只有二核苷酸重复,相邻的条表示相差一个重复单位的等位基因频率。(来自 Valdes、slatkin 和 Freimer 1993。)
Payseur 2010),但实际上它通常是单独报告的,甚至没有对采样的染色体数量进行校正。
有两种常见的微卫星变异统计摘要
确实提供了在逐步突变模型下和 Wright-Fisher 平衡种群中 θ 的估计值。第一个公式使用样本的预期纯合性 F,其计算方法如下:
是基因座上第 i 个等位基因的频率(在 K 个总等位基因中)。
令人困惑的是,与公式 3.1 中所示的核苷酸杂合性计算不同,常用的纯合性计算不使用
Bessel 的偏差校正(n/[n − 1] 项)。但是,由于杂合子和纯合子的比例之和必须等于 1,我们还必须将未校正的杂合度 H 定义为 1 − F。根据这种计算样本纯合度的方法,我们可以将微卫星位点的参数 θ 的估计量定义为 (Ohta and Kimura 1973):
尽管 θF 是 θ 的一个略有偏差的估计量,但可以通过基于模拟的改进来减少这种偏差 (Xu and Fu 2004)。
在逐步突变模型下,微卫星位点的 θ 的第二个估计量使用在单个位点 V 观察到的等位基因重复次数的方差。由于微卫星突变通常会产生与原始状态相距一个或几个重复单元的新等位基因,因此重复次数的方差可以很好地指示位点上保持的变异量。如果我们假设只可能发生单步突变,并且突变增加或减少重复单元的概率相等,则 E(V) = θ(Moran 1975;Goldstein 等人 1995;Slatkin 1995)。因此,θ 的直接估计量由以下公式给出:
虽然这个估计量是无偏的,但它的方差很大(Zhivotovsky 和 Feldman 1995)。这里提供的所有汇总统计数据只是逐步突变模型和标准中性模型的所有其他假设下参数 θ 的估计量。但是,可以在广义逐步模型下推导出 θ 的估计量,该模型具有关于添加或减去的平均重复单元数以及重复增加或丢失的任何不对称性的任意属性(Kimmel 和 Chakraborty 1996)。虽然这些估计量确实需要指定要使用的特定突变模型——并且这种模型中的许多参数对于任何特定基因座都是未知的——但似乎即使是一些假设 SMM 的估计量也可能对模型错误指定具有相对稳健性(Xu 和 Fu 2004;Haasl 和 Payseur 2010)。单倍型变异
如果核苷酸序列数据是分阶段的(无论是通过实验还是计算),那么图 3.1 中的 4 个序列代表 4 种单倍型,而图 3.2A 中的 10 个序列代表 10 种单倍型。图 3.1 中还有 4 种独特的单倍型,所有序列都代表不同的核苷酸组合(这些有时也称为等位基因;参见第 1 章)。图 3.2A 有 8 种独特的单倍型。如果没有重组,新的单倍型只能通过突变产生,独特单倍型的数量 K(有时也表示为 ne)最多为 S + 1。如果重组率高,则可以通过重组和突变产生新的单倍型,因此最多可以有 2S 种不同的单倍型。假设 Wright-Fisher 种群处于平衡状态,且无限等位基因突变模型没有重组(第 1 章),则基因座处独特单倍型的预期数量 K 与种群突变参数 θ 之间存在关系:
= + + + + + + + −
其中 n 再次是采样染色体的数量(Ewens 1972)。通常需要使用数值优化来求解此处的 θ,我将把这个 θ 估计量称为 θK
。请记住,在这种情况下,突变率 μ 测量基因座处突变为新的中性等位基因(即独特单倍型)的速率。总结单倍型变异的其他方法使用 Equa 的类似物tion 3.21 来计算单倍型纯合性:唯一的变化是
表示 K 个独特单倍型中第 i 个独特单倍型的频率。同样,这个值通常被称为 F,其中 H = 1 − F 用于计算单倍型杂合性(也称为单倍型多样性;Depaulis
和 Veuille 1998)。单倍型杂合性和独特单倍型的数量显然极大地依赖于单个核苷酸的包含,因为每个单个核苷酸都会创建一个新的单倍型。因此,通常可以看到这两个统计数据在计算时都不包括这些突变。
虽然在处理(大部分)非重组序列(如线粒体 DNA 或 Y 染色体)时将单倍型视为变异单位很有用,但许多重组核基因座的研究都集中在核苷酸位点变异上。值得注意的是,上述总结核苷酸多样性的统计数据并不依赖于单倍型的准确定相:即使单倍型是从同一组分离位点随机构建的,π、θW 和所有其他基于核苷酸的统计数据的值也不会改变。话虽如此,单倍型在检测自然选择方面有许多具体用途,稍后将讨论(见第 8 章)。重组 4
在上一章中,我们考虑了多种描述 DNA 序列样本多样性的方法,从分离位点数量的总结,到微卫星位点等位基因的数量,再到独特单倍型的数量。这些统计数据(包括基于分阶段单倍型的统计数据)都旨在总结突变在产生多样性方面的影响。在本章中,我将介绍多种总结重组在产生分子多样性方面的影响的方法,包括位点对之间和重组区域内。虽然我们检测重组的能力需要存在核苷酸变异,但重组在单倍型之间重新分配这些变体方面的影响与突变的影响截然不同。我首先描述检查重组对双基因座基因型的影响的方法,然后介绍重组的区域和全基因组摘要。
测量连锁不平衡
连锁和连锁不平衡
从一个个体收集两个单倍型意味着我们正在观察结合形成个体的两个亲本配子。也就是说,我们有在初始受精卵中结合在一起的母系和父系衍生的染色体。当然,这些序列本身不一定是母系或父系基因组中存在的单倍型,而是可能代表一种新的重组单倍型,它是亲本基因组中存在的两个单倍型的组合,并作为配子传递。连锁是指配子中位点的共同遗传,因为它们在染色体上物理相连。
图 4.1 给出了一个在两个基因座 (A1
) 上杂合且具有两个单倍型 A1 的个体的例子。
该个体产生的四种可能配子是 A1
。如果两个基因座紧密相连,那么几乎所有的配子都将是 A1
。如果两个基因座完全不相连,那么所有四个配子预计在减数分裂期间以相同的频率产生。我们将两个基因座之间的重组频率 c 定义为产生的 A1
配子的分数。
图 4.1 连锁。左边的例子显示两个紧密连锁的基因座,因此只产生两个亲本配子(c = 0),而右边的例子显示两个不连锁的基因座,所有四个配子以相等的频率产生(c = 0.5)。
因此,c = 0.5 意味着两个基因座不连锁,而 c < 0.5 意味着它们是连锁的。
正如连锁被定义为等位基因通过减数分裂的关联一样,连锁不平衡 (LD) 被定义为种群中等位基因的非随机关联。这个术语有点误导,因为连锁基因座不一定处于连锁不平衡中,甚至不连锁的基因座也可能处于连锁不平衡中。但物理连锁是 LD 的主要原因——事实上,许多紧密连锁的位点都处于 LD 中——这导致许多人将这两个术语混为一谈(关联不平衡可能是这种现象的更好选择)。如果两个基因座在群体中随机相互关联,那么第一个基因座上的 A1 并不能告诉我们第二个基因座是否会是 B1。但如果它们是非随机关联的(即连锁不平衡),那么具有 A1 的个体也可能更有可能具有 B1。如果我们将 pi 定义为第一个基因座上等位基因 Ai 的频率,将 qj 定义为第二个基因座上等位基因 Bj 的频率,并且如果等位基因之间存在随机关联,我们可以发现只需将两个基因座上的单个等位基因频率相乘即可得到预期的单倍型频率 gij。这些基因座被称为处于连锁平衡状态。但是,如果等位基因之间存在关联,那么这些预期值就会偏离一定量 D,我们将其定义为连锁不平衡系数(Robbins 1918;Lewontin 和 Kojima 1960)。如果我们考虑由两个各有两个等位基因的基因座产生的四种单倍型组合,我们可以更清楚地看到这一点。单倍型出现的频率为:当没有连锁不平衡(D = 0)时,单倍型频率恰好等于组成等位基因频率的乘积。但是
在存在 LD 的情况下,所有单倍型频率都会偏离量 D。
请注意,我们选择将 D 添加到 A1
单倍型并从 A1
中减去它是任意的:D 本身可以是正的也可以是负的,并且在这种情况下对于每个单倍型都必须相同,这样我们对连锁不平衡程度的推断就不会受到这种选择的影响。但是,在“耦合”阶段(即 A1
)将 D 添加到单倍型并从“排斥”阶段(即 A1
)的单倍型中减去 D 是标准做法。虽然在种群样本中耦合和排斥类型的分配也是任意的,但 Langley、Tobari、RECombinATion 和 Kojima (1974) 建议将包含两个较常见等位基因和两个较不常见等位基因的单倍型视为耦合,并且这种命名法已成为相对标准。其他命名系统,例如将祖先-祖先和衍生-衍生突变对分配为耦合阶段,也可能有用(例如,Langley 和 Crow 1974;Machado 等人 2002;Takahasi 和 Innan 2008)。
成对连锁不平衡的测量
根据上述定义,很容易看出,不平衡系数 D 可以按以下方式计算:
适用于任何等位基因组合。由于与观察到的单倍型频率的偏差只能与边际等位基因频率的乘积一样大,因此 D 的范围和值取决于 pi 。例如,= 0.5 和 q1 = 0.5,D 可以在 -0.25 和 +0.25 之间变化,而当 = 0.1 和 q1 = 0.7 时,D 介于 -0.07 和 +0.03 之间。这意味着位点对之间 D 值之间的差异既可以反映等位基因之间关联强度的差异,也可以反映等位基因频率的差异。为了能够比较位点对之间的连锁不平衡水平,Lewontin (1964) 建议使用以下标准化测量方法:
, ) , 表示 0
, ) , 表示 0
其中 max(x,y) 表示 x 和 y 中较大的一个,min(x,y) 表示较小的一个。
D′ 的值现在限制在 −1 和 +1 之间,尽管通常只报告绝对值。请注意,虽然 D′ 的范围不再取决于等位基因频率,但该统计数据的值(事实上所有连锁不平衡测量值)仍然取决于等位基因频率(Lewontin 1988)。
第二种常用的连锁不平衡测量方法是基于两个基因座等位基因的平方相关性,由 Hill 和 Robertson (1968) 首次提出:
这里使用统计量 r2 代替等位基因状态的相关性 r (=D/√[p1
]),以消除与计算 D 相关的符号。
因此,r2 统计量受 0 和 1 的限制。除了 r2 的值对边际等位基因频率的依赖性比 D′ 略低之外,
它还是一种有用的统计量,因为它与种群重组参数 r 相关(见下文)。
连锁不平衡的两个测量方法 D′ 和 r2 也提供了有关等位基因之间关联的非常不同的信息。简而言之,虽然 D′ 告诉我们两个基因座之间的重组,但 r2 告诉我们我们的能力,即根据另一个基因座的等位基因状态,预测一个基因座等位基因的身份。要了解这一点,请考虑图 4.2 中给出的示例。在此样本 (A1) 中仅观察到三种独特的单倍型,因此 D′ 将等于 1(有时称为完全 LD)。事实上,除非观察到所有四种单倍型组合,否则 D′ 始终为 1,而这只有在两个基因座之间发生重组时才有可能(复发突变的情况除外,在这种情况下,所有四种单倍型都可以存在而无需重组)。这些限制是四配子重组测试的基础(Hudson 和 Kaplan 1985;另见下文)。相比之下,从图 4.2 中的样本计算出的 r2 值为 0.111。该值如此之低是因为在了解 A 基因座的等位基因的情况下,几乎没有能力预测 B 基因座的等位基因,即使h 没有发生重组。除非一个种群中只有两种单倍型,并且它们各自在两个基因座上都含有替代等位基因(通常称为完美 LD),否则 r2 将始终小于 1。r2 的这一特性使其在表型性状的关联(连锁不平衡)映射中非常有用,其中的问题更多地围绕着预测不同表型状态背后的基因型,而不是重组的存在。
无论使用哪种统计数据,计算任何观察到的连锁不平衡的重要性都很简单。
一种方法是将四种可能的单倍型的计数排列在 2×2 列联表中,如图 4.3 所示。然后可以将任何独立性检验(例如 Fisher 精确检验)应用于这些计数,以询问 D 是否与 0 有显著差异(在所示示例中 P = 1.0)。第二种方法源于 nr2 服从 c2 分布,自由度为 1(其中 n 表示采样的分阶段单倍型的数量)。在这种情况下,c2 统计量为 10 * 0.111 = 1.11,这也不显著。由于当次要等位基因频率较低时(样本量不是很大),很难获得显著的 r2 值,因此通常会忽略涉及次要等位基因频率 <0.05 的多态性的计算。在处理基因组规模的数据集时,必须考虑计算连锁不平衡的几个细微差别(有关单倍型的实验和计算定相问题的讨论,请参见第 2 章)。一个常见的问题是缺失数据:具有准确基因型信息的位点之间的染色体数量可能经常存在差异。由于无法在个体中定义一对位点的单倍型,而其中一个位点的状态未知,因此每对位点的样本量可能不同。在存在缺失数据的情况下正确计算 D′ 或 r2 要求将具有至少一个未定义位点的任何个体从两个位点的单倍型计数和等位基因频率计数中移除,并相应调整样本量和等位基因频率。此要求显然仅适用于涉及缺失数据的位点的 RECombinATion 成对比较;相同的采样染色体可用于其他比较,这些比较在两个位点都定义了基因型。无论是通过测序还是基因分型平台获得,都会出现缺失数据,并且可以从任一数据源计算连锁不平衡。然而,基因分型方法(如 SNP 芯片)固有的确定偏差意味着连锁不平衡的总体水平也可能存在偏差(Akey 等人,2003 年)。需要明确的是:连锁不平衡的个别测量不会因任何一对位点而产生偏差,但许多对之间的平均不平衡水平将相对于理想群体的期望而产生偏差(有关这些期望,请参见下文)。可能并不令人意外的是,由于它们使用的数据方面不同,确定偏差对 D′ 和 r2 的影响也大不相同(Nielsen 和 Signorovitch 2003)。确定偏差导致中频多态性的过度表达,这意味着 D′ 倾向于向下偏差,而 r2 倾向于向上偏差,尽管如果知道原始确定方案,这两种偏差都可以纠正(Nielsen 和 Signorovitch 2003)。
总结成对连锁不平衡
计算许多分离位点对的连锁不平衡系数——无论是在一个区域内还是来自整个基因组——都会提供大量数据。那么问题就变成了:我们如何理解所有这些数据?有许多方法可以总结成对 LD,其主要区别在于目的是提供局部还是全局的连锁不平衡视图。局部视图试图总结单个区域内的 LD 模式,而全局视图可能总结多个区域甚至整个基因组的 LD。
有两种简单的方法可以总结区域内的成对连锁不平衡,一种是图形方法,另一种是简单地使用所有成对测量值的平均值。Kelly (1997) 将 n 个序列样本中 S 个分离位点的平均 r2 值定义为:
(之所以选择 Z,是因为它是 John Kelly 最喜欢的字母。)与 r2 一样,
的值在 0 和 1 之间变化,表示某个基因座的平均成对 LD。
如果没有重组,平衡状态下的 ZnS
平均值预计约为 0.15(Kelly 1997)。位点内重组会导致 ZnS 的值降低,而某些形式的选择可以提高 ZnS 的值。Rozas 等人 (2001) 提出了一种 ZnS 的修改方法,可用于检测是否发生了重组通过测量相距越来越远的位点对之间的 LD 下降来比较 ZnS。然而,ZnS 最常用于检测自然选择(见第 8 章)。图 4.4 显示了果蝇 su(wa) 基因座(Langley 等人,2000 年)中某个区域的成对连锁不平衡的图形摘要。显著的成对比较用彩色框表示,与 0 显著不同的 D 的成对比较用彩色框表示(P < 0.01;Fisher 精确检验)。仅比较在 51 条采样染色体中至少 2 条上发生的多态性。虚线将分离位点的位置与其在矩阵中的对应列连接起来。(来自 Langley 等人,2000 年。)低 P 值表示存在连锁不平衡的证据(相当于图 4.3 中所示的检验)。我们可以在这个例子中看到,许多(但不是全部)相邻的多态性彼此之间有显著关联,而且相距近 2,000 个碱基的多态性之间也存在一些显著关联。否则,该区域的连锁不平衡模式没有太多结构,LD 不会延伸很远,这对于果蝇来说是典型的。相比之下,图 4.5 提供了人类 500 kb 区域中成对 LD 的图形摘要(国际 HapMap 联盟,2005 年)。在此表示中,只有 D′ = 1 的多态性对用彩色框表示;更多的对具有
D′ > 0。该图中区域 LD 的一个显著特征是由于人类重组的点状性质:由于重组主要发生在染色体上有限数量的位置(Jeffreys、Kauppi 和 Neumann 2001;McVean 等人 2004),因此存在大块非常高的 LD,它们几乎可以独立于相邻块。这些所谓的
单倍型块可以包括数百种彼此完全连锁不平衡的多态性,重组“热点”将各个块分开。尽管用于定义单倍型区块的标准可能因研究而异,但此类区块是迄今为止研究的哺乳动物种群的共同特征(例如,Guryev 等人,2006 年;Villa-Angulo 等人,2009 年)。
区域 LD 的简单表示,例如图 4.4 和
RECombinATion
图 4.5 东亚智人 2q37.1 区域中的成对连锁不平衡。D ′ = 1 的成对比较用彩色框表示。
(来自国际 Hapmap Consortium 2005。)
4.5 可以是一种相对直接的方式来可视化基因座和物种之间 LD 和重组模式的差异。
为了更全面地了解整个基因组的连锁不平衡,显然我们不能使用图 4.4 和 4.5 中所示的图表类型——我们需要为每条染色体绘制单独的图表,并且每个三角矩阵都必须非常大才能包含整个染色体。当然,我们可以给出一个统计量,即所有位点对的平均 LD,但这种总结并没有提供大量有关 LD 在基因组中结构方式的信息。一个常见的基因组(或较小区域)LD 总结是 LD 低于某个阈值的距离,旨在揭示 LD 的规模。通常,这个阈值是 r2 的任意值(例如,r2 < 0.2)或平均 r2 低于初始值 50% 的距离(即相邻碱基多态性之间的值)。
图 4.6 显示的正是这种连锁不平衡衰减的显示。在豆科植物模型苜蓿(Medicago trunculata)的基因组中,绘制了相距小于 20 kb 的多态性之间约 350,000 次比较的 r2 值(Branca 等人,2011 年)。26 个苜蓿近交系(n = 26)的整个基因组已经测序,并且显示了所有相距小于 20 kb 的 SNP 之间的 r2 值分布(涵盖所有 8 条组装染色体)。 (LD 可以在插入/缺失之间计算,
或者实际上在任何变体之间计算,但在本例中没有这样做。)我们可以看到
r2 值有很大的差异,许多对在非常短的距离处具有 r2 = 0,而在距离高达 7 kb 时具有 r2 = 1。该图显示 M. trunculata 中的 LD 规模约为 5 kb;也就是说,对于相距约 5 kb 的 SNP,平均 LD 低于
r2 = 0.2,并且下降到
其初始值的一半以下
2 到 3 kb。这个数字当然是在许多不同的
区域内平均的,每个区域可能都有自己的重组率。因此,观察到的 LD 的衰减可能在每个区域内都不同,总结
SNP 之间的距离(以 kb 为单位)
图 4.6 连锁不平衡的衰减um 横跨 M. trunculata 基因组。
粗红线表示相距 20 kb 以内的所有多态性对之间的 r2 平均值(未显示单个点)。 50% 范围的值以深蓝色显示,90% 范围的值以浅蓝色显示。(来自
branca 等人,2011 年。)
图 4.6 中显示的表示全基因组平均重组率的成对 LD 下降;下面的公式 4.11 和 4.12 提供了在给定平均重组率和基因座之间的种群大小的情况下对这种衰减的理论预期。 虽然该图没有显示相距超过 20 kb 的多态性之间的 r2 值,但我们预计平均 r2 最终会下降到未连锁基因座的 1/n。
扩展到多个等位基因、多个基因座和基因型
到目前为止讨论的连锁不平衡测量仅考虑了两个基因座(每个基因座有两个等位基因)之间的比较,或这种成对测量的总结。我们还假设我们知道染色体上等位基因的相位,因此也只考虑了同一染色体上基因座之间的不平衡。在这里,我简要讨论了依次放宽这些限制的 LD 测量;更多详细信息可在 Weir (1996) 中找到。
当一个或两个基因座上有多个等位基因时,必须为每对等位基因计算单独的不平衡系数:
与两个等位基因的情况不同,为两个以上等位基因计算的系数在所有对之间并不相等。但是,与双等位基因的情况一样,所有 Dij 值的总和必须为 0,并且任何特定 i 或 j 的所有 Dij 值的总和也必须等于 0(例如,如果第二个基因座有三个等位基因,则 RECombinATion
除了成对连锁不平衡之外,我们还可以考虑两个以上基因座之间的不平衡。所有 LD 的高阶测量都可以从三基因座的情况中轻松得出,因此我在这里仅讨论三基因座不平衡。给定三个基因座 A、B 和 C,其等位基因频率为 pi
我们想知道在所有三个基因座的等位基因组之间是否存在非随机关联,而这种关联不能由等位基因对之间的非随机关联来解释。为了回答这个问题,我们在计算中包括了成对不平衡系数:
对于三个以上基因座之间的不平衡也进行了类似的计算,
始终考虑所有低阶不平衡。重要的是要认识到,这些测量值不是总结区域 LD,而是测试两个以上基因座之间的高阶相互作用。
到目前为止讨论的所有计算连锁不平衡的方法都假设所有个体都有已知相位:染色体上等位基因的排列是已知的。因此,通常将先前的统计数据称为配子连锁不平衡的度量。但如果相位未知——要么是因为两个位点在一条染色体上相距很远,要么是因为它们位于不同的染色体上——我们仍然可以询问两个基因座的基因型之间是否存在非随机关联(例如,图 4.7),这种状态称为基因型连锁不平衡。假设两个基因座各有两个等位基因,则每个基因座有三种不同的可能基因型 ) 和九种不同的基因型组合 (图 4.8)。如果我们将 A1 个体的频率表示为 ,将 A1 个体的频率表示为 g1112 ,将 A1 个体的频率表示为 g1211 ,将 A1 个体的频率表示为 g1212 ,则基因型不平衡系数可计算为 (Weir 1979): + 0.5g1212 对于图 4.7 中所示的九种二倍体基因型样本,∆ = 0.136。假设种群处于 Hardy-Weinberg 平衡状态,图 4.7 来自种群的九种二倍体基因型样本。 A 和 B 基因座之间的连锁关系(以及配子阶段)未知。
图 4.8 基于图 4.7 中显示的个体,样本中双基因座基因型的计数。
重要性可以再次使用 3 × 3 基因型表上的独立性检验来评估(图 4.8)。
如果已知单倍型之间存在随机交配,则这种基因型不平衡估计值也等同于配子不平衡系数 D。假设 18 种单倍体基因型中的每一种(例如,图 4.7 中的 A1 代表一个分阶段的单倍型,则此样本的 D = 0.123,与我们的基因型不平衡系数相似。
估计重组
查找样本中重组事件的最小数量
到目前为止讨论的统计数据主要局限于分离位点之间的成对比较,因此只能告诉您特定位点对之间重组的影响。但是,我们希望能够对重组在单个区域和整个基因组中的影响做出更普遍的推断。在此下一节我将介绍总结重组效应的多种方法。这里我们首先介绍用于估计单个区域序列样本中必须发生的最少重组事件数的方法。正如前面解释 D′ 和 r2 之间的差异时提到的,可以使用四配子检验 (Hudson and Kaplan 1985) 推断出群体遗传数据集中重组的确凿证据。该检验的本质是,在两个基因座中,每个基因座都有两个等位基因,在无限位点假设下,产生所有四个可能配子的唯一方法是在两个基因座之间的某个地方发生重组事件。无限位点假设很重要,因为等位基因的复发突变可以在不发生重组的情况下产生所有四个配子。例如,图 4.2 显示了一组仅存在三种单倍型的序列样本:A1
但是,如果 B1
突变复发,并且发生在背景中,则所有四个配子都将存在于种群中,并且
可能存在于染色体样本中。
当然,仅仅观察所有四个配子并不能告诉我们样本历史上发生了多少次
重组事件,只能告诉我们
至少发生了一次事件(模复发突变)。
估计样本中的重组事件数 R 实际上非常困难:与样本中的分离位点数 S 不同,R
不能直接观察到。许多重组事件可能发生在一组序列的历史中,但无法观察到,要么是因为它们没有发生在祖先中处于杂合状态的两个位点之间,要么是因为它们产生了样本中已经存在的重组单倍型。然而,我们可以估计样本中必须发生的重组事件的最小数量,这个数字通常比 R 小得多,因为大多数重组事件 RECombinATion 都无法检测到(Hudson 和 Kaplan 1985;Stephens 1986;Posada 和 Crandall 2001)。有两个常用统计数据用于限制样本中重组事件的最小数量:Rm(Hudson 和 Kaplan 1985)(Myers 和 Griffiths 2003)。 Rm
根据四配子检验确定区域中必须发生重组的最大非重叠间隔数。Rh
基于以下观察:在具有 K 个独特单倍型和 S 多态性的任何区域中,重组事件的数量必须满足 R ≥ K − S − 1。因此,可以通过 K − S − 1 来估计最小重组事件数。对于较长的序列,这种关系会失效,特别是当分离位点的数量大于不同单倍型的数量时(这当然受采样染色体数量 n 的限制)。但是,通过将来自每个具有 K ≥ S + 1 的多个位点子集的最小重组估计值组合在一起,Rh
可以为整个区域内重组事件的全局最小数量提供一个界限。用于查找 Rm 的算法还提供了推断的重组事件的位置。一般来说,Rh 的估计值比 Rm 更准确,因此(Myers 和 Griffiths 2003)。要了解为什么会出现这种情况,请考虑图 4.9 中给出的示例。在此示例中,我们有四个位点(1-4)和八个采样染色体(a-h),每个染色体都有一个独特的单倍型(K = 8)。计算 Rm 的算法如下(图 4.9 中的示例有明确结果):
1. 对于所有位点 i 和 j 对,确定所有四个配子是否
• 图 4.9:(1,2)、(1,3)、(1,4)、(2,4)和(3,4)
2. 删除完全包含其他区间的区间,包括具有相同起点或终点的区间。
• 图 4.9:删除(1,3)、(1,4)和(2,4)
图 4.9
3. 如果任何剩余区间重叠,则转到步骤 4;如果不是,则转到步骤 5。
• 图 4.9:转到步骤 5
4. 对于第一对位点(按起始点递增顺序列出)(i1),删除任何带有 i1 的区间(m,n)
下一个不重叠对(i2),删除任何带有 的区间(m,n),重复此过程,直到没有重叠区间。
• 图 4.9:没有这样的区间
5. 剩余区间的数量表示重组事件的最小数量,并且分配一个事件在每个区间发生。
八个采样染色体(n = 8)中四个分离位点的单倍型示例。
每个多态性
有两个等位基因,
任意表示为
0 或 1。每个四基因座单倍型都是
唯一的,因此 K = 8。
对于此示例,
= 2 和 Rh
(有关详细信息,请参阅文本)。
• 图 4.9:区间 (1,2) 和 (3,4) 中的重组事件
(根据 myers 和
Griffiths 2003。)
在此示例中,Rm
= 2,Hudson-Kaplan 算法表示,位点 1 和 2 之间必须发生至少
一次重组事件,并且位点 3 和 4 之间至少有一个。相反,Rh = 3(= 8 − 4 − 1),而 Myers-Griffiths 算法(参见 Myers 和 Griffiths 2003)表示所有位点对之间必须发生至少一次重组事件。我们可以直观地了解 Hudson-Kaplan 算法为什么错过了重组事件(位点 2 和 3 之间),因为注意到这对位点只有三个单倍型。然而,这些位点之间确实发生的重组事件产生了一个新的四位点单倍型,Myers Griffiths 算法会将其考虑在内,因此推断出的重组事件的最小数量更大。存在许多其他算法来找到
更准确的最小重组事件数界限
(例如,Song 和 Hein 2005),尽管对于大量样本和多态性,它们在计算上变得难以处理。
群体重组参数
许多进化过程会影响特定区域中连锁不平衡的估计水平:重组、自然选择、漂移、人口历史,甚至突变(最后一种,因为如果没有足够的多态性,许多重组事件将无法检测到)。然而,正如我们在第 1 章中看到的那样,在标准中性模型下,影响序列样本中重组量的唯一因素(无论是否可检测)是每个位点的重组率 c 和有效种群大小 Ne ,它与遗传漂移的幅度成正比。我们将常染色体位点的群体重组参数定义为 r ≡ 4Ne 。 (r 有时称为 C 或 R,而 c 通常称为
r。为了在使用希腊字母命名参数时保持一致,并避免
r 和 r2 之间的混淆,我们将使用此处给出的符号。)在标准中性模型的假设下,r 与样本中的重组事件数呈正相关,与连锁不平衡量呈负相关。具体而言,大小为 n 的样本中重组事件的预期数量由 (Hudson
and Kaplan 1985) 给出:
R 的这个期望与第 3 章中给出的分离位点数 S 的期望形式完全相同,只是 q 被 r 取代。正如
q 不等于突变率一样,r 也不等于重组率,但预计在染色体上与重组率高度相关。
事实上,人类谱系研究中 c 的估计值与 r 的估计值高度相关(例如,McVean 等人,2004 年),尽管这些测量值之间的局部偏差可能表明自然选择的作用(O’Reilly、
Birney 和 Balding,2008 年)。
重新组合
在关于 r 是大还是小、样本大小以及在计算 r2 之前是否去除低频等位基因的略有不同的假设下,已经得出了 r2 和 r 的预期值之间的多种关系。假设样本量无限大且 r 值较小,则 r2 与 r 之间的经典关系为 (Sved 1971):
此公式无法校正小样本量,并且错误地预测当 r = 0 时(即在完全链接的位点之间)的平均值 r2 = 1(回想一下,只有当一对位点的边际等位基因频率完全相同时,r2 才能等于 1)。另一种关系(Weir 和 Hill 1986;Hill 和 Weir 1988)可校正有限样本量,并在排除低频率等位基因(<10%)时为较小的 r 提供正确的预期:
) 1 (3 )(12 12
此公式不适用于较大的 r 值——特别是,当 r 大到足以使位点有效地脱钩时,它不会预测 r2 的值为 1/n。
对于 r = 0 和非常大的样本量,它预测 r2 的值为 5/11,类似于无限样本量的其他结果(Ohta 和 Kimura 1971;McVean 2002)。
公式 4.11 和 4.12 中给出的关系为我们提供了一种将重组水平和连锁不平衡联系在一起的方法。就不同种群之间的比较而言大小,这些结果预测在具有较大规模的群体中 LD 水平较低(假设每个位点的重组率相等)。非洲和非非洲人类种群之间的比较证实了这一预测,由于人类迁出非洲时瓶颈导致有效种群规模减少,非洲人的 LD 远低于非非洲人(国际 HapMap 联盟 2005)。就一对分离位点而言,c 的适当值是分离位点的核苷酸数量的倍数,因此对于相邻核苷酸的多态性,r = 4Ne
c,对于相距 L 个核苷酸的多态性,r = 4Ne
c(L-1)。这意味着,对于相距越来越远的位点,r 会增加,并且,将越来越大的 r 值代入公式 4.12,预计 r2 会沿着近似指数衰减染色体。
图 4.6 显示了 r2 与多态性之间的距离之间的这种递减关系。事实上,我们可以使用公式 4.12 和如图 4.6 所示绘制的数据来找到任何特定数据集的最佳拟合值 r(例如,Brown 等人,2004 年)。虽然这个 r 估计值代表了绘制的所有区域的平均值,但还有更准确的方法来估计 r。接下来我将描述其中一些方法。
估计种群重组参数
用于描述核苷酸变异的常见汇总统计数据(所有这些都是在适当假设下对参数 q 的估计)与用于估计重组参数 r 的统计数据之间存在两个重要差异。首先,用于描述核苷酸变异的统计数据(例如,公式 3.2、3.5、3.8、3.9 和 3.10)都是序列多样性的直接描述,即使平衡 Wright Fisher 模型的假设不成立,也很容易解释。虽然重组效应的总结(例如 K、ZnS)或多或少容易解释,但这些都不是 r 的估计量,尽管它们可以间接用于估计此参数(见下文)。相反,最准确、最常用的估计量采用近似似然法,假设标准中性模型来计算似然,研究人员并不总是清楚这些方法的作用。虽然提供对其功能的直觉并不是精确方法的必要条件,但在违反标准中性模型假设的情况下,统计数据应该是可解释的。第二个更重要的区别是,r 的估计量远不如 q 的估计量准确。也就是说,即使我们处理的是符合标准中性模型假设的群体,这些估计量在正确估计群体重组参数方面的表现也会比 q 的等效估计量差得多,尤其是在 r 较低且分离位点很少的情况下(Wall 2000a;Hudson 2001)。对多态性水平的依赖尤其令人不安,因为这意味着在突变率低的地区,或在由于选择或近期人口规模变化而导致多样性水平降低的地区,r 的估计值会有偏差。尽管存在所有这些警告,但估计这些统计数据已被证明在许多应用中很有用。与 q 的估计量一样,r 也有基于矩和基于似然的估计量。完全似然法(例如,Griffiths 和 Marjoram 1996;Kuhner、Yamato 和 Felsenstein 2000;Nielsen 2000;Fearnhead 和 Donnelly 2001)计算量非常大,而且考虑到可分析数据集的大小限制,它们与近似似然法相比提供的准确度(如果有的话)可能很小。因此,我重点介绍基于矩的估计量和多种形式的近似似然估计量。
基于矩的 r 估计量基于这样的观点:取样染色体之间的成对差异的方差(即 p 的方差)随着重组的增加而下降(Hudson 1987;Wakeley 1997)。要了解为什么会出现这种情况,请想象一个在所有分离位点对之间具有最大 LD 的样本:无论有多少多态性,这样的样本都只包含两个单倍型。因此,将存在最大方差——两个不同单倍型之间的所有比较都将导致每个多态性核苷酸的差异,而同一单倍型样本之间的所有比较都没有核苷酸差异。重组的作用是将样本分解成更多独特的单倍型,从而减少成对差异的方差。此描述还强调了估计 r 和 q 之间的另一个区别:与基于矩的 q 估计量 RECombinATion 不同,后者都使用分离位点数分布的一阶矩(即平均值),而 r 的估计量使用二阶矩(即方差)。Wakeley (1997) 略微改进了 Hudson (1987) 首次提出的估计量;这个改进的估计量表示为 rp,是目前使用最广泛的基于矩的估计量。我们之前看到(公式 3.3),通过使用所有序列对 i 和 j 之间的核苷酸差异数 (kij),我们可以计算 p 如下:
基于此,我们可以计算 p 的方差如下:
Wakeley (1997) 表明,重组样本中 S2 的期望取决于参数 r 和 q,方式很复杂,但可用于估计 rp
不幸的是,rp 是一个比基于各种似然法的估计量更有偏差的估计量;Hudson (1987) 早期基于矩的方法甚至更糟(Wall 2000a;Hudson 2001)。幸运的是,有四种不同的方法可以找到基于似然性的 r 估计量。这些方法都不能被认为是完全似然方法,因为它们都使用了这样或那样的近似值,但总的来说,它们比完全似然方法在准确性、计算效率和速度方面都有所提高。其中两种方法可以简要总结一下:Hey 和 Wakeley (1997) 表明,对于 n = 4 和 S = 3 的样本,可以精确计算出 r 的似然估计值。对于大于此的样本,他们的估计量 rg(他们称之为 g)对四个序列的所有可能子集中的每组三个相邻的多态性取平均估计值。总体而言,rg 似乎给出了略微向下偏向的 r 估计值(Hey 和 Wakeley 1997;Hudson 2001)。Li 和 Stephens(2003)提出的另一种方法利用了这样一个事实:看到任何特定单倍型的概率取决于样本中的所有其他单倍型以及 r 和 q 的值。样本中每个单倍型的条件概率都不同,但可以通过使用马尔可夫链蒙特卡罗(MCMC)方法对整个样本中的所有单倍型取平均值来找到最大化可能性的 r 值(我将其称为 rLS)。在程序 PHASE(Li 和 Stephens 2003)中,可以在从未定相的数据重建单倍型的同时估计 rLS。第三种方法(Wall 2000a)使用有时称为近似似然法的方法(有关详细信息,请参阅第 9 章)。该方法首先计算样本的几个汇总统计数据,例如 K 和 ,然后模拟样本数量和分离点数量的等效数据集,以 r 的许多值表示。给定任何特定的 r 值,观察到的汇总统计数据的概率是具有相同统计数据的试验的比例。最大似然估计量定义为最大化该比例的 r 值。估计量 rK ——实际上是找到一个 r 值,使观察到的单倍型数量 (K) 最大化,或者使单倍型数量和最小重组事件数量 (K 和 Rm) 最大化,这种方法被证明效果最好 (Wall 2000a;请注意,本文将单倍型数量称为 H)。作为 Wall 方法的一个应用示例,图 4.10 显示了针对单个 r 值进行一次此类模拟运行的结果。如果在样本中我们观察到 K = 10,则该图中的结果表明,在 r = 0.03(每个位点)的情况下,K = 10 的概率约为 0.079。也就是说,在 1,000 次随机模拟中,r = 0.03,样本大小和分离位点数量相同,只有 79 次模拟会产生K = 10。当 r = 0.03 时,这显然不是最可能的结果,因此较小的参数值可能会最大化看到 K = 10 的概率。对 r 的一系列值进行类似的模拟将使我们能够找到最大似然估计 rK。在找到 rKRM 的最大似然 (ML) 估计量时,我们需要找到最大化 K 和 Rm 观测值概率乘积的 r 值;因此,我们还必须记录给定特定 r 值的 Rm 概率。近似似然法易于实现,可用于为许多不同类型的参数找到最大似然估计量,而无需似然函数(例如,Andolfatto 2007)。事实上,很容易看出,给定观察到的分离位点数量,也可以模拟许多不同的 q 值来找到最大化观察到的 S 可能性的该参数的估计值。但是,简单的基于矩的方法提供同样准确(且更快)的 q 估计值,因此在这种情况下可能性方法通常是不必要的。概率(K|ρ = 0.03)图 4.10 给定 r = 0.03 查找观察到 K 个单倍型的概率。运行了一千次合并模拟,其中 n = 20、S = 10 和 r = 0.03,并记录每次模拟运行的唯一单倍型数量 K。 3 4 5 6 7 8 9 10
RECombinATion
我在这里考虑的 r 的最终估计量现在也是最广泛使用的估计量之一,部分是因为它的准确性,部分是因为实现它的软件包易于使用。这个估计量的最初想法来自 Hudson (2001),他证明了在给定不同的 r 值的情况下可以快速计算出双位点抽样分布,从而可以进行“复合”可能性估计 rCL
(第 9 章还更详细地讨论了复合可能性方法)。
双位点抽样分布在某些方面类似于上一章中描述的等位基因频谱。预期ed 等位基因频率谱表示单个多态性的概率密度函数,即在样本中以任何特定频率发现单个变体的概率。双位点抽样分布表示一对位点的概率密度函数,具体来说,所有四种可能的双位点单倍型————都会出现在特定的频率组合中(例如 g11 = 1)。特定双位点样本配置的概率取决于 r,因此,我们可以通过模拟许多具有不同 r 值(假设 q 较小)的双位点样本来找到 r 的最大似然估计值,类似于上面描述的 Wall (2000a) 的方法。 Hudson (2001) 的关键见解是表明,可以将许多对链接位点的单个 ML 估计值(每个位点之间的距离可能不同,因此它们之间的重组率可能不同)组合起来,为整个数据集生成一个单一的复合似然估计值 rCL。由于这是一种复合似然方法,因此该估计值的平均值将反映真实平均值,但由于各个 ML 估计值之间的不独立性,置信区间将比预期的要窄。数据引导法已用于生成 rCL 估计值的准确界限,但这在计算上可能很昂贵。一种用于准确估计复合似然计算中的置信区间的较新方法是使用 Godambe 信息矩阵(Coffman 等人,2016 年),它可以快速有效地计算不确定性。复合似然估计器已得到改进,包括允许在同一位点发生多个突变的可能性(即有限位点模型;McVean、Awadalla 和 Fearnhead 2002)以及允许 rCL 值沿染色体变化(McVean 等人 2004)。在复合似然框架中,缺失数据也很容易处理。允许 rCL 值变化的能力特别强大,尤其是在处理区域内重组率差异很大的物种时(例如,图 4.11)。尽管程序 LDhat
(McVean、Awadalla 和 Fearnhead 2002)和 LDhelmet (Chan、Jenkins 和 Song 2012)使用 MCMC 方法来估计染色体上的可变重组模式,并且此类方法通常计算量更大,但获得的信息通常可以抵消所需的稍长运行时间。
性别平均重组率
位置(kb)
图 4.11 人类 HLA 区域中群体遗传数据(红色)和直接配子基因分型(蓝色)的重组率估计值比较。rCL 的估计值(红线)已通过假设人类有效种群大小的单一值和 c 转换为重组率。 (根据 mcVean 等人 2004 年的研究;基于 Jeffreys、Kauppi 和 neumann 2001 年的研究。)
最后,应该对这里讨论的所有 r 估计量做一点评论。与上一章讨论的 q 估计量一样,所有这些统计数据都只是在 Wright-Fisher 平衡种群和适当的突变模型假设下估计 4Ne
c 的数量。如果这些假设不成立,那么我们的统计数据肯定会与样本中的重组量有关,但我们不知道确切的关系。在比较 q 和 r 的估计量时,这个问题尤其严重。在标准中性模型的假设下,q/r = 4Ne
c = m/c,因此这些参数的比率告诉我们基因位点突变和重组的相对重要性。但是,除非所有假设都成立,否则诸如 qW
之类的统计数据将无法准确估计 q 和 r,因此 qW
不等于 m/c。即使违反我们的模型似乎提供了一种直接估计等效平衡值的方法(如人口瓶颈),各个估计量的特殊行为也很难确保我们估计的是 m/c。例如,估计量 qW
和 p 在人口瓶颈之后以不同的速率恢复到其平衡值(参见第 9 章),因此非平衡人口中的统计数据选择将极大地影响结果。这意味着 r 的各种估计量恢复到其预期值的速率也可能有很大差异。总之,虽然对群体重组和群体突变参数的估计量的比较让我们对重组和突变的相对大小有了一些了解,但这个比率通常不等于 m/c。
基因转换
重组
到目前为止,在我们对重组影响的研究中,我们只考虑了交叉在打破位点间关联方面的作用。正如我们之前所看到的,然而,基因转换是重组的另一种结果(第 1 章)。
在连锁不平衡模式方面,交叉和基因转换之间的主要区别在于每种模式的影响程度。
交叉的影响随着物理距离的增加而增加,LD 根据公式 4.11 和 4.12 中给出的关系衰减。然而,由于基因转换片段(即转换的 DNA 片段)相对较短 - 大约为 100 到 1,000 个核苷酸(Chen、Cooper 等人,2007 年) - 该过程只会对紧密链接的位点产生影响,并且对于相距足够远的标记,该过程应该与距离无关(Andolfatto 和 Nordborg,1998 年;Wiehe 等人,2000 年)。要了解为什么会出现这种情况,请考虑图 4.12 中给出的示例,其中基因转换仅限于相对较小序列段,仅影响所示的三种多态性中的一种。如果我们想象一个群体,其中在所示的转换事件之前仅存在 A1 单倍型,则 A1 单倍型的产生显然会减少 A 和 B 基因座等位基因之间以及 B 和 C 基因座等位基因之间的关联。但是,对 A 和 C 基因座之间的连锁不平衡没有影响,因为转换事件不会改变转换道两侧基因座之间的关系。这样,转换道两侧基因座的结果类似于双交叉的结果,仅在受影响序列的长度上有所不同。因此,基因转换预计对紧密连锁位点的影响大于对较远位点的影响,而交叉在远距离上占主导地位。自然种群中的连锁不平衡模式与转换的重要作用一致,紧密连锁变体之间的 LD 低于如果交叉是重组的唯一机制所预期的 LD(Langley 等人,2000 年;Ardlie 等人,2001 年;Frisse 等人,2001 年)。事实上,许多估计基因转换影响的方法都依赖于小规模和大规模 LD 之间的对比(例如,Padhukasahasram 等人,2006 年)。 Hudson 的复合似然估计量 rCL 和类似方法 (Wall 2004) 可以很容易地改变,以另外估计基因转换与交叉的比率 (f) 和平均束长度 (q),后者被认为是几何分布的 (Hilliker 等人 1994)。所有用于检测基因转换的方法的主要问题是,如果没有大量数据,许多此类事件将被遗漏 (Wiuf 和 Hein 2000);即使有 转换前 转换后 图 4.12 等位基因转换的影响。上图显示了一个在三个基因座 A、B 和 C 上杂合的二倍体个体。基因转换事件发生在减数分裂期间(上图中虚线箭头所示),等位基因 B2 作为供体,B1 作为受体。结果是额外的 B2 携带配子。大量数据,如果平均束长度远小于平均多态性间距离,那么几乎不可能准确估计束长度分布(但请参阅 Miller 等人 2012 年的可能方法)。基于沿序列的多态性分布的替代方法 - 并且不试图估计 r - 提供了基因转换的明确测试,但也会错过较短的束,并且如果转换过于猖獗以至于整个序列均质化(Sawyer 1989),则不会检测到任何事件。种群结构 5
种群分化
种群、亚种群和群落
如第 2 章所述,从分子种群遗传数据集得出的推论可能对所采样的精确个体非常敏感,尤其是个体是否全部来自同一种群。我所说的种群是指一群自由杂交的二倍体个体;该术语对自交或无性谱系的定义更具争议性。虽然它们有时可以用来表示略有不同的事物,但亚种群或群落这些术语通常与种群含义相同,我将交替使用它们。除了在特定情况下,一般会避免使用含义更丰富的术语种族和亚种。物种可以细分为任意数量的种群,无论它们是完全分离的(即它们不交换任何迁徙者)还是仅部分分离的(即它们交换一些迁徙者)。正如没有特定的遗传距离阈值来区分不同的物种一样,也没有特定的阈值来将两组个体称为不同的种群。正如下面将要讨论的那样,从分子数据中实际识别种群的问题可以归结为识别自由杂交的个体群体的问题——但完全随机交配的理论理想在现实生物中很少甚至从未实现。此外,种群可能已经分离了不同的时间,或者它们之间的关系可能存在某种系统发育结构(例如,种群 A 和 B 彼此之间的关系比它们与 C 之间的关系更密切)。如果亚种群尚未达到迁移-漂移平衡,则用于推理的模型的许多假设可能会被违反。如果亚种群没有完全杂交,任何改变种群内等位基因频率的进化力量(突变、选择、漂移、迁移)都可能导致它们之间的这些频率差异(图 5.1)。然后这些种群被称为分化的(我通常将“分化”一词保留为物种之间的差异)。分化导致种群结构
种群 1
种群 2
图 5.1 两个种群的例子,每个种群的等位基因 A 和 a 都是多态的。种群 1 中 A 等位基因的频率为 p1,种群 2 中为 p2(请注意,p1 的总和不必为 1)。
在群体之间,这仅仅意味着种群内的个体往往比种群之间的个体更紧密相关。显然,昨天才完全停止交换移民的种群并没有自由杂交,但它们也不会表现出任何结构。
这个关于种群的简单讨论引出了两个非常重要的问题:(1)我们如何衡量种群之间的差异?(2)我们如何在实践中定义种群?虽然我将在第 9 章中讨论推断人口人口历史的许多方法,但上述问题对人口遗传数据分析的重要性要求我们在此解决这些问题。此外,人口结构研究比分子数据的出现早了几十年,并且在某种程度上独立于推断人口历史的其他方法而发展。因此,它值得进行充分的讨论,特别是考虑到目前用于测量人口差异和定义人口的许多方法。我们依次处理这些主题;但是,通过首先了解 Wahlund 效应,可以更好地理解我们两个问题的答案。
Wahlund 效应
Hardy-Weinberg 平衡下的基因型频率的简单预期(第 1 章)提供了一个强有力的零假设,我们可以据此检验随机交配假设的偏离情况。一个基因座或种群可能脱离哈代-温伯格平衡的原因有很多,并非所有原因都涉及非随机交配甚至自然选择(Waples 2015)。然而,种群结构可能导致偏离 HWE,因为它会在种群之间产生强烈的非随机交配。当对多个亚群进行采样而不知道底层结构时,就会偏离 HWE:即使所有单个亚群本身都在 HWE 中,总体“种群”也可能远离 HWE 预期。这种偏离预期的形式总是相同的——观察到的杂合子个体比 HWE 下的预期要少。这种杂合子缺陷被称为 Wahlund 效应,以瑞典遗传学家 Sten Gösta William Wahlund 的名字命名,他首次描述了这种采样类型的后果(Wahlund 1928)。要了解杂合子不足的原因,请考虑图 5.1 中的两个种群。我们将种群 1 中 A 等位基因的频率表示为,将种群 1 中 a 等位基因的频率表示为 q1(我们在这里使用此符号,以免将等位基因 A1 与种群 1 和 2 混淆)。在种群 1 中,p1 = 0.8 和 q1 = 0.2,而在种群 2 中,p2 = 0.8(请注意,p1 不必等于 1,因为这些是来自两个不同种群的相同等位基因的频率)。如果我们从每个种群中抽取了相同数量的个体,则两个种群的平均等位基因频率,即种群结构 p,为 0.5,因此预计所有个体中有 50% (=2) 在 HWE 下是杂合的。但是,样本中观察到的杂合子比例将约为 ),这比预期值低得多。通过进行更多这样的计算,您会注意到,与 Hardy-Weinberg 期望值的偏差幅度与等位基因频率的差异成正比:与等位基因频率差异很大的种群相比,等位基因频率相似的种群在分组时与 HWE 的偏差非常小。因为我们经常要处理两个以上的亚群,所以种群间等位基因频率差异的一个有用度量是频率方差 s2。因此,一般来说,Wahlund 效应对预期每种基因型的频率可以表示为:
其中再次表示种群中等位基因的平均频率,pAA表示基因座上三种不同二倍体基因型的频率。等位基因频率的方差越大,纯合子越多,杂合子越少,当种群固定为替代等位基因时,获得的最大方差(=0.25)导致没有观察到杂合子。这些关系表明,种群间等位基因频率的方差可能是量化与 HWE 偏差的一种好方法,因此也是衡量种群间分化程度的一种好方法。我们将看到,对方差的轻微修改是衡量种群分化的理想方法,它将理论预测与数据联系起来。测量种群分化
使用 FST 测量种群分化
给定一个物种内多个种群的多个个体样本,我们希望能够说出这些种群的差异有多大。 暂且不论我们计算这些差异的确切方式,实际上有多种其他方法来总结分化。 我们可以询问多个种群之间的平均细分量,或询问所有种群之间的成对关系。 我们也可能拥有非常不同的数据类型,从单个多态性位点(或多个未链接位点)的等位基因频率到编码或非编码区域中的完整单倍型序列。 处理两个或两个以上亚群的方法大致相同,但测量单个位点与整个序列的分化的许多不同方法通常不同; 因此,我们首先讨论单个多态性位点的分化。在上述关于 Wahlund 效应的讨论中,我们看到,种群间等位基因频率的差异是衡量分化的自然方式,并且它与基因型频率的理论预期很好地相关。然而,等位基因频率的差异本身并不是一个非常有用的统计数据,因为它的值高度依赖于平均等位基因频率。假设每代都对等位基因进行二项式抽样,平均等位基因频率为 p = 0.5 的基因座在种群间表现出的差异将比从完全相同的个体中抽样但 p = 0.01 的基因座高得多。这意味着很难比较不同基因座之间或不同种群组之间的差异。为了用最大可能的方差来标准化方差,我们可以定义一个新的分化统计量:其中 s2 是等位基因 A 在人群中频率的观测样本方差,是等位基因 A 在人群中的平均频率,是等位基因 a 在人群中的平均频率(=1 − )。图 5.1 中显示的人群的值为 0.09/0.25 = 0.36。该度量首先由 Wright(1931、1943、1951)提出,他将其定义为亚群之间的分化量,并表明它对任何频率的中性等位基因都具有相同的预期值。就我们的目的而言,下标“ST”并不是真正必要的,但它将此度量与此处未涵盖的类似 HWE 偏差度量(具体而言,FIS ,其中“I”代表“个体”,“S”代表“亚群”,“T”代表“总群体”,这是 Wright 的原始符号)区分开来。作为群体分化的度量,它具有一些非常好的特性。它的范围在 0 到 1 之间,0 表示没有分化,1 表示不同亚群中替代等位基因的完全固定。有很多不同的方法可以理解 FST 到底代表什么,但我们可以通过简单的代数将其与 Wahlund 效应联系起来:
该方程表示,当没有分化(FST = 0)时,杂合子不存在缺陷,但当完全分化(FST)时,杂合子完全缺失。因此,FST 可以被认为是 Wahlund 效应大小的量度。或者,人们可以将其视为一组种群中总变异量的量度,该量度由种群间方差而不是种群内方差来解释,或者作为亚种群内等位基因与总种群之间的相关性(Holsinger and Weir 2009)。
已成为一种使用分子数据量化种群分化的非常流行的方法。然而,计算“FST”的方法有很多种。与估计核苷酸的许多不同统计数据一样多样性
参数 q(第 3 章),还有许多不同的方法来计算
FST 类统计数据。与核苷酸多样性测量的另一个相似之处是
人口结构
通常(且容易混淆)用于表示参数和统计数据——即既是与人口模型相关的理论构造,又是从数据中估计该参数的精确方法。更令人困惑的是,一个常见的 FST 类统计数据被表示为 q(Cockerham 1969;Weir 和 Cockerham 1984)!参数和统计数据的这种混合可以追溯到 Wright 对 FST 的原始定义,我不会尝试理清符号或引入我自己的新符号来区分相互竞争的用法(在本章中,我也不得不以两种方式使用该术语)。但是,应该意识到,用于量化种群内和种群间相对变异量的许多不同统计数据和参数都称为 FST。如果在亚群中采样的染色体数量相同,则公式 5.2 是在“固定”效应模型(下文进一步解释)下估计 FST 的无偏方法。如果样本量不相等,则计算此统计数据的更好方法是:其中对于所有 K 个亚群,每个亚群 i 的样本量 ni 样本等位基因频率 pi ,并且整个数据集的平均样本量 n 和平均样本等位基因频率(Weir 1996)。请注意,如果所有亚群的样本量相同(即所有 ni 都相等),则此公式简化为公式 5.2。从同一组种群中的分离点计算出的 FST 值存在相当大的差异。这是因为产生种群结构的进化过程(见下文)具有很大的随机成分,导致 FST 的实际值范围很广。在看似严格的关于潜在种群结构的假设下,Lewontin 和 Krakauer (1973) 表明,变换后的 值应为 c2 分布,自由度为 K − 1(其中 K 再次是亚种群的数量)。尽管更复杂(但不一定更现实),但已经得出了 FST 方差的预期(例如,Nei 和 Chakravarti 1977;Weir 等人 2005),c2 近似值似乎非常符合从自然种群收集的数据。图 5.2 显示了四个人类种群中从整个基因组计算出的 FST 分布。请注意,FST 中存在很大的方差,并且它与具有三个自由度的 c2 分布非常相似(Weir 等人,2005 年)。Cockerham(1969 年)指出,上面给出的计算方法仅考虑了种群内个体的采样。如果研究目标是一组固定的种群,那么这种“固定”效应模型是完全合适的。固定效应模型也更适用于种群数量有限的情况——例如人类。但是,如果我们试图将从一小部分种群中获取的 FST 值与更大的种群联系起来,那么我们还必须考虑与不仅种群内个体采样相关的随机性,而且还要考虑物种内种群的采样。 Weir 和 Cockerham (1984) 随后展示了 FST 类参数如何对人类基因组产生影响。数据来自四个人类群体中 1 号染色体上的 599,356 个 SnP。(Weir 等人,2005 年之后)他们称之为 q 的等式可以在这种“随机”效应模型下进行估计,以便使用方差分析 (ANOVA) 方法更好地整合多级抽样。当然,随机效应模型更合适的条件也是非常理想化的:所有亚种群必须彼此平等相关,并且具有相同的种群规模,并且所有亚种群之间的迁移率必须相同(相当于无限岛模型;参见第 1 章)。满足这些条件的物种可能很少。此外,当从大量亚群中抽取大量样本时,随机效应模型会收敛到固定效应模型(Weir 1996)。因此,固定效应估计量(公式 5.2 或 5.4)可能适用于许多研究。
Wright 原始公式的首次修改之一是由 Nei (1973) 进行的,他引入了一种当一个基因座有两个以上等位基因时计算 FST 的方法。 Nei 将他的统计量称为 GST
(当只有两个等位基因时,它相当于统计量 FST
),并将其定义为:
是根据所有子群体中的所有个体的所有 i 个等位基因的频率计算得出的总采样群体(个体)中的预期杂合度:
= − −∑ (5.6)
是从每个采样子群体(每个子群体都有自己的样本大小 nS
)分别计算得出的预期杂合度的平均值:
请注意,数量 HT
有时被称为 DST
(Nei 1973)。
这些杂合度的定义与以下定义非常相似公式 3.1 给出了这些值,但现在它们是根据种群结构的层次结构定义的。根据图 5.1 中所示的种群计算出的 GST 值为 (0.526 − 0.356)/0.526 = 0.323,与使用公式 5.2 获得的值相似。在测量具有两个以上等位基因的位点的种群分化时出现的一个问题是 GST 不考虑等位基因的身份。因此,两个种群可能不共享任何等位基因,但种群结构不会有 GST = 1。要了解原因,请注意,当 HS 不为 0 时,GST 会小于 1,即使分化可能已经完成(即没有共享等位基因)。种群分化度量对种群内变异的依赖性是本文描述的许多统计数据的共同点,将在下一节进一步讨论。为了克服对其最大可能值的依赖,Hedrick (2005) 提出了一个标准化统计量 G′ST,类似于第 4 章介绍的标准化连锁不平衡系数 D′。然而,G′ST 本身存在许多问题,不能与 FST 的参数期望相关(Whitlock 2011)。对于具有许多等位基因的基因座(例如微卫星),我们可以通过明确考虑突变过程,从而考虑等位基因之间的突变距离来克服 GST 的局限性。对于采用逐步突变模型并假设岛屿模型的微卫星位点,Slatkin (1995) 表明,他所称的 RST 统计量可用作参数 FST 的估计量。该统计量的计算方法如下:
是所有亚群所有样本中单个位点上观察到的等位基因的重复次数(或等位基因大小,当不知道确切的重复次数时)的方差,VS
是每个亚群内重复次数的平均方差。我们之前已经看到过使用微卫星等位基因大小方差的统计量,qV(公式 3.23);为了保持一致性,我们将继续使用那里引入的符号,但请注意,“S”通常用于表示公式 5.8(Slatkin 1995)中的方差。我们还可以看到,使用等位基因频率(公式 5.2、5.4 和 5.5)测量种群分化与使用等位基因大小(公式 5.8)测量种群分化之间存在令人愉悦的对称性:两者都基于种群内和种群之间的方差差异。RST 通常比 GST 更准确地推断微卫星,至少在逐步突变模型成立时如此。当它不成立时,RST 也可能有偏差(Balloux 等人,2000 年)。为了从全序列数据计算 FST
,我们可以使用一个基因座上的位点杂合性总和(Nei 1982):
根据公式 3.2 计算,使用跨亚群的所有样本组合,而 pS
是分别对每个亚群进行相同计算的平均值(数量 pT
有时也称为
)。因此,统计量 gST
类似于
的多位点版本,因此,正如 Nei(1982,第 172 页)所述,“显然,pT
对应于 HT
”在单位点分析中(显然)。Slatkin
(1991)表明 gST
是岛屿模型的 Wright 参数 FST
假设的估计量。已经提出了类似的统计数据来衡量从完整序列数据(通常是单倍型)进行的种群分化,包括对单个位点的多个突变的校正。Lynch 和 Crease(1990)提出了一种测量方法,他们称他们的统计数据为 NST。两者的一个重要区别是,前者在计算 pT 值时包括来自同一亚群的序列之间的比较,而后者则没有(请参阅下文的类似测量)。这意味着 NST 不是 FST 的估计量,尽管 NST 会收敛到大量采样种群(Lynch 和 Crease 1990)。Excoffier、Smouse 和 Quattro(1992)又增加了一项新内容,他们基于序列之间的单倍型差异引入了 Weir 和 Cockerham(1984)的 ANOVA 框架的扩展;他们的统计数据表示为 fST。 Excoffier、Smouse 和 Quattro 的分子变异分析 (AMOVA) 方法与其他使用全序列数据的方法不同,它不使用位点杂合性的总和,而是需要完整的单倍型。这是因为它考虑了数据集中所有单倍型对之间的核苷酸差异数量,然后将得到的距离矩阵转换为层次方差分量。因此,fST 通常应用于线粒体 DNA (mtDNA) 数据,尽管实际上可以为微卫星等位基因生成类似的距离矩阵,并且 fST 也可以用于这种数据(Michalakis 和 Excoffier 1996)。与标准方差分析不同,在 Weir 和 Cockerham (1984) 的 ANOVA 方法和 Excoffier、S小鼠和 Quattro (1992) 的 AMOVA 方法中,方差分量(因此 )可以为负数,而不必全部加起来为 1;在所有分析中,将负值设置为 0 是标准做法。有关这些种群分化测量方法之间的差异和相似之处的讨论,请参阅 Excoffier (2007)。种群分化的替代测量方法及其相关统计数据只是总结种群分化的一种方式。已经提出了替代方法(有时也会使用),这些方法基于私有等位基因(仅在一个种群中出现的等位基因;Slatkin 1985)、共享等位基因(Bowcock 等人 1994)、等位基因频率的绝对差异(或其平方根变换值;Cavalli-Sforza 和 Edwards 1967)、基因座上没有重组时的基因树拓扑结构(Slatkin 和 Maddison 1989;Hudson、Slatkin 和 Maddison 1992)以及种群间纯合性的差异(Nei 1972)。最后一个测量值(称为 Nei 的 D)一直是用于等位酶和微卫星数据的遗传距离的特别流行的测量值,对于这些基因座,可能有许多等位基因。 Nei (1972) 将一对种群的某个基因座的统计量定义为:
种群结构 分别是种群 X 和 Y 中某个基因座的第 i 个等位基因的频率。在这些计算中,JX 表示种群 X 中所有等位基因的预期总纯合度(假设随机交配),JY 表示种群 Y 中所有等位基因的预期总纯合度,JXY 表示如果种群 X 和 Y 具有完全相同的等位基因频率,则所有等位基因的预期总纯合度。如果两个种群在相同的样本频率下具有相同的等位基因,则 D = 0。种群之间等位基因频率的差异越大,D 值就越大。与 FST 之类的统计数据不同,Nei 的 D 取决于基因座的突变率。虽然独立于突变率似乎使 FST 和相关统计数据更加可靠,但在解释这些测量值在不同基因座之间的差异时,仍然存在重要的警告。
上述所有类似 FST 的统计数据的一个非常重要的方面是,它们受到亚群内变异水平的强烈影响(Charlesworth 1998;Jakobsson、Edge 和 Rosenberg 2013)。 因此,我们将它们称为相对分化测量。 相反,种群分化的绝对测量大多独立于种群内多样性水平;绝对测量也称为遗传距离。 对种群内变异水平的依赖意味着类似 FST 的统计数据的值会因标记类型(SNP、微卫星等)的不同而不同,这仅仅是因为标记间的平均杂合度不同(例如,Moyle 2006)。对种群内多样性的依赖还意味着,从基因组中多样性较多或较少的部分采集的相同类型的标记将提供截然不同的分化水平视图。例如,来自重组减少的区域(由于连锁选择,这些区域的多样性通常会降低)的 FST 将高于正常重组的区域,原因仅仅是核苷酸多样性的总体水平不同(Charlesworth、Nordborg 和 Charlesworth 1997;Charlesworth 1998;Noor 和 Bennett 2009;Cruickshank 和 Hahn 2014)。为了解决这个问题,Nei(1973)提出计算两个种群序列之间成对差异的平均数量,不包括种群内序列之间的所有比较。我将把这个统计数据称为 dXY,尽管在文献中它也被称为 pXY(和 Li 1979)、DXY(Nei 1987)和 pB(Charlesworth 1998)。这种绝对的分化测量与所比较的两个种群内的多样性水平无关(但取决于突变率)。它的计算方法如下(Nei 和 Li 1979;Nei 1987,等式 10.20):分别是种群 X 中第 i 个单倍型和种群 Y 中第 j 个单倍型的频率,kij 是每个种群中单倍型对之间的核苷酸差异数。这个等式类似于我们计算种群内单倍型间平均差异数的方式(等式 3.3),尽管这里我们只计算种群之间的差异。的方差在 Nei (1987, eq. 10.24) 中给出。请注意,dXY 也可以从非相位数据中计算出来,其中 xi 表示等位基因频率,kij 为 1 或 0,具体取决于等位基因在单个位点是否不同。然后将各个位点的值相加以获得全基因座测量值。dXY 也可以使用来自每个种群的单个序列来计算,因为它具有与发散统计量 d 相同的期望值(参见第 7 章)。是一系列基于 dXY 的相对分化测量指标,应用广泛。在两个种群 X 和 Y 中,我们将种群内的多样性水平称为 dX,分别用样本 X 中的 p 和样本 Y 中的 p 计算。Nei 和 Li (1979) 将两个种群之间的“净”核苷酸差异测量 da(他们称之为 d)定义为:
该统计数据(通常也称为 Da
)旨在仅捕获自种群分裂以来积累的差异。它通过减去分裂前积累的差异(见图 7.1)来实现,假设祖先变异水平等于两个当前种群中发现的变异的平均值。因此,da 是一个相对测量指标,因为它的值会受到种群内变异量的强烈影响。 (令人困惑的是,Nei [1987] 在不同的地方将此统计数据称为 da、d 和 Dm。)我们还可以将种群或物种之间的固定差异数表示为 df(例如,Ellegren 等人,2012 年)。固定差异数也是一个相对度量,因为它依赖于种群内的变化。要了解这些绝对和相对度量如何产生不同的结果,请考虑图 5.3 中给出的示例。图 5.3A 显示了具有平均重组率的区域中某个基因座的两个种群的一个假设谱系历史(有关基因谱系的详细讨论,请参阅第 6 章)。种群内多样性水平与每个种群样本最近的共同祖先的时间成正比,因此相对于其历史的种群间部分而言较高。在这种情况下, 较高,而 da 相应较低,因为它们依赖于种群内变异。另一方面,图 5.3B 显示了来自低重组区域的基因座的假设谱系历史,该基因座取自与图 5.3A 完全相同的种群和个体。由于连锁选择,在这种情况下,种群内最近的共同祖先的时间非常近。这意味着 dX 较低,而 da 相应较高;dXY 在两个图中完全相同。这样,da 可以为来自同一种群的基因座提供非常不同的结果,因为两个基因座依赖于种群内变异,而一个则不依赖。因此,Charlesworth (1998, p.538) 建议,相对分化测量“不一定适合于我们想要比较种群内变异水平非常不同的基因座”。
许多种群分化测量依赖于相对多样性水平的最后一个含义是,它们可能会受到确定偏差的影响。要理解原因,请回想一下确定的主要原因
种群结构
种群 X
种群 Y
种群 X
图 5.3 演示 dX 之间的差异
(B) 都显示了与两个种群(X 和 Y)的四个采样染色体(A、B、C 和 D)相关的示例谱系。统计数据 dX 分别测量种群 X 和 Y 中样本之间的平均核苷酸差异数。 dXY 测量种群 X 中每个样本与种群 Y 中每个样本之间的平均核苷酸差异数,不进行种群内的比较。da 表示 dXY 之间的差异(公式 5.12 和 5.13),df 表示固定差异的总数。(A)和(B)之间的重要区别在于,两个面板之间的 dX 存在差异,但 dXY 没有差异。为简单起见,两个面板中的谱系具有相同的高度,每个图中种群 X 和 Y 内的融合时间也相同。情况不一定如此,但它使区分此处描述的各种度量变得更容易。存在偏见的原因是,中频多态性更有可能在小型“发现”个体样本中观察到。这意味着,种群频率接近 0.5 的分离位点将在确定的标记集中过度代表。这种确定偏差对汇总统计数据的影响很复杂(Rosenblum 和 Novembre 2007;Albrechtsen、Nielsen 和 Nielsen 2010),但会影响许多关于种群结构的推断,包括 FST 的值(Clark 等人 2005)、推断的种群间迁移率(Wakeley 等人 2001)以及种群本身的结构(Foll、Beaumont 和 Gaggiotti 2008;Guillot 和 Foll 2009)。是否有证据表明某个基因座存在种群分化?上述所有用于测量种群分化的统计数据都提供了对种群在等位基因频率上差异程度的一些定量评估。一旦这些测量有了这些样本,我们就可以利用它们推断出所采样种群的结构以及可能导致观察到的任何差异的进化力量。
种群 Y
种群 1
种群 2
图 5.4 图 5.1 中的等位基因计数。计数分别显示种群 1 和种群 2 中的 A 和 a 等位基因数量。对这些数据进行 χ2 检验(由于每个单元格中的计数较小,因此使用连续性校正)得出 P = 0.025。
我们可以提出的最简单的问题是是否有任何证据表明存在种群结构 — 即样本是否来自一个混血种群。有多种方法可以检验种群结构的证据,包括如果已经从个体收集了基因型数据,则检验是否偏离哈迪-温伯格平衡(参见前面关于 Wahlund 效应的讨论)。如果尚未收集基因型数据,我们仍然可以通过比较拟议亚群之间的等位基因频率来检验结构。进行此测试的最简单方法是使用 c2 检验或其他等位基因计数独立性检验(参见 Goudet 等人,1996 年)。使用图 5.1 中的等位基因计数,我们可以通过如图 5.4 所示排列数据来应用此类检验。通过应用 c2 检验,我们发现这些等位基因计数来自一个单一种群的概率为 P = 0.025,因此这两个亚群很可能存在差异。
我们还可以根据这些等位基因计数,用统计学术语来提出我们的问题,例如 FST 及其相关测量。测试种群结构相当于测试 FST = 0 的零假设。获取此类测试的 P 值的一种直接方法是多次在种群中置换样本,从而生成零值分布(Hudson、Boos 和 Kaplan 1992)。然后,P 值基于模拟分布中观测值的位置;因此,P 值为 0.01 要求观测值高于除 1% 之外的所有置换值。对于单个多态性位点,使用 FST 进行测试似乎并没有比等位基因计数(Hudson、Boos 和 Kaplan 1992)具有太大优势,但对于包含多个分离位点的较长序列,由于位点之间的不独立性,必须使用置换方法。这种方法将为观察到的数据计算 gST 或其他基于序列的分化统计数据(例如,Hudson 2000),然后多次置换亚群中的个体单倍型以生成零分布。正如我所描述的那样,使用等位基因计数的方法和使用分化汇总统计数据的方法都在测试无结构的零假设。那么应该显而易见的是,样本大小和效应大小之间存在紧密的关系,当对大量染色体进行采样时,即使是非常小的分化水平也可以检测到。换句话说,如果有足够的数据,低至 FST = 0.001 的值可能具有重要意义,并且仅表明存在某种低水平的人口结构。因此,决定是否应合并或拆分亚群取决于样本量和要解决的特定问题(参见 Waples 和 Gaggiotti 2006)。对于何时说两个种群是分化的,没有单一的规则,并且大多数研究可能不会受到将分化水平为种群结构 = 0.001 的亚群合并的影响。相反,最近使用数十万个标记物的研究可以检测到重要的地理结构模式,即使平均值为 0.004(Novembre 等人,2008 年)。在本章后面,我将讨论使用信息论方法确定具有多个基因座的种群结构的几种方法,这些方法使我们能够对提出更多亚群时数据拟合度增加的情况做出似然陈述。一旦我们确定存在显着的种群结构,我们如何解释我们对分化的总结?“很多”或“一点”分化是多少?Wright(1978,第 85 页)给出了以下指导方针:“我们将 FST = 0.25 作为一个任意值,高于该值时分化非常大,0.15 到 0.25 的范围表示中等分化。但是,如果小到 0.05 甚至更小,分化绝不能忽略不计。”这些解释是否应该在所有情况下使用 - 或者仅仅作为经验法则 - 是不可能知道的,特别是当结果取决于所使用的标记时。此外,
从人口分化数据中得出的最有趣的推论将不仅限于 FST 任何特定值的大小或含义,而是与推动这种分化的进化力量有关。进化过程对分化的影响
自然选择对种群分化的影响
种群间等位基因频率的差异是由改变种群内等位基因频率的相同过程驱动的:突变、
自然选择、遗传漂变和迁移。突变的影响将始终非常小,并且主要限于将新的等位基因引入个体种群。复发性突变有时会将状态相同的等位基因引入不同的亚种群,但发生此类事件的概率很低,取决于 q(Clark 1997)。然而,
选择、漂变和迁移——以及这些力量之间的相互作用——可能会对种群分化产生非常大的影响。该领域的大部分近期工作都集中在梳理这些力量产生的模式。
我将首先关注自然选择对种群间差异的总体影响,并回到第 10 章中用于识别特定选择位点的方法。正如预期的那样,自然选择对种群分化的影响对于不同的选择形式非常不同:弱负选择、平衡选择和正选择可以产生高度独特的分化模式。这意味着我们可以在一定程度上区分这些影响,尽管在中性情况下仍然很难区分它们。强负选择当然会阻止任何变体达到可观的种群频率,因此对分离多态性的分化影响不大。然而,弱负选择允许变体以低频率分离,但限制了可能的等位基因频率范围。这种限制意味着,对于弱有害变体,平均 FST 将低于能够漂移到任何频率的典型中性变体(图 5.5)。此外,虽然平衡选择也会降低 FST(见下一段),但只有弱负选择会导致变异在每个种群中的频率较低;平衡选择下的多态性可能处于任何频率。我们预计,在采样种群中受到相同(或非常相似)选择压力的平衡多态性在种群中的频率相似。如前所述,在这种情况下,选择再次限制了可能的等位基因频率的范围,这意味着与中性多态性相比,种群之间的等位基因频率变化会更小。所有这些都意味着平衡选择将降低 FST。这种选择的典型例子是人类的 ABO 血型基因座:A、B 和 O 等位基因存在于几乎每个人类群体中,但等位基因频率范围很窄(Brues 1954;Chung 和 Morton 1961)。尽管作用于该基因的平衡选择的具体形式尚不清楚,但 ABO 基因座除了非常低的 FST 外,还显示出平衡选择的多种分子特征(Stajich 和 Hahn 2005;Calafell 等人 2008)。
中性突变
有害突变
FST < 0.05 的 SNP 比例(%)
中性突变
有害突变
1 3 5 10 15
图 5.5 负选择对 FST 的影响
。显示了模拟两个种群之间共享的中性和
选择多态性的结果,平均 FST
设置为 0.11(相当于人类种群之间的平均分化)。
随着对有害突变的选择增加,(A)平均 FST
降低,并且
(B)所有 FST
<0.05 的多态性的比例增加。(Barreiro
等人,2008 年。)
种群结构
任何对物种内所有亚群起类似作用的正向选择预计不会导致亚群之间的分化,除非当一个新的有利等位基因连续扫过每个种群时(但参见 Bierne 2010)。然而,仅限于种群子集的正向选择(称为局部适应)可能导致等位基因频率的巨大差异。 (这种空间变化选择形式有时被称为平衡选择,因为多态性在物种水平上得以维持。在研究种群分化的背景下,我只会将维持亚群内多态性的过程称为平衡。)在极端情况下,在一种环境中极其有害的等位基因在另一种环境中可能非常有利:在这种情况下,等位基因频率在密切相关的种群之间可能从 0 到 1 不等。在这种情况下,选定的多态性可以显示 FST = 1,即使在大多数基因组中没有分化(例如,Turner 等人,2010 年)。在不太极端的情况下,正向和负向效应的影响有害选择将被视为 FST 值分布上尾中选定多态性的过量。图 5.6 显示了人类基因组中具有 FST 的非同义 SNP 的大量过量;对于 FST < 0.05 的非同义 SNP,即分布下尾中的有害多态性,也观察到了类似的过量(Barreiro 等人,2008 年)。这种过量是相对于假定受到很少直接选择的多态性(在此示例中为非基因 SNP)来衡量的。但是因为 FST
和等位基因频率并不完全独立,所以正确的统计比较必须比较多态性
SNP 比例 (%) 与 FST > 0.65
2.2 × 10−15
4.3 × 10−12
3.9 × 10−3
图 5.6 人类基因组中正向选择的影响。在四个人类群体中,总共对 851,856 个 SnP 进行了基因分型,并根据 Excoffier、Smouse 和 Quattro (1992) 的方法进行了 FST。FST 分布上尾的非同义多态性大量过剩与正向选择的作用一致(P 值表示与非基因 SnP 相比过剩)。编码区域中的连锁选择很可能增加了此尾部中同义多态性的比例。(Barreiro 等人,2008 年)从选定和未选定的位点类别中获取频率相似的短语,以检查选择对种群分化的影响(例如,Barreiro 等人,2008 年;Langley 等人,2012 年)。
迁移和漂移对种群分化的影响
对于中性多态性,种群分化模式将由迁移、漂移和连锁选择决定。连锁选择显然对靠近选定多态性的中性多态性有影响——例如,参见图 5.6 中同义多态性的 FST 模式——它生成的模式将是找到特定区域的关键,这些区域是空间变化选择的目标(参见第 10 章)。
同义
非同义
连锁选择也会对与选择目标松散关联的大片基因组的 FST 估计值产生影响,因此整个基因组的分化将是显示该过程不同影响的基因座的混合体(Nosil、Funk 和 Ortiz-Barrientos 2009)。由于连锁选择的结果主要是减少或增加局部 Ne,因此在本章的其余部分,我将简单地将此机制视为确定种群分化水平的漂移项的一部分。种群分化主要由迁移和漂移的相反力量决定。为了理解迁移和漂移对种群分化的不同影响,解释亚种群历史的两个对立模型是有益的:恰当命名的迁移和隔离模型(Wakeley 1996a)。考虑两个经常被问到的关于亚种群(有时是物种)的问题:(1)它们多久前分裂的?(2)它们之间有多少次迁徙?事实证明,所选择的种群历史模型将从根本上影响这些问题的答案。
迁移模型本质上是 Wright 的无限岛模型(第 1 章)。
在这个模型中,亚种群之间的迁移使等位基因频率同质化,而漂移引起的采样会导致等位基因频率的差异。在迁移模型中,所有亚种群都已达到迁移-漂移平衡,因此不再有任何分裂的历史信号(图 5.7A-C)。在下面列举的大量假设下,Wright (1931) 表明,统计 FST 常染色体基因座的预期值为:是每个亚种群的大小(假定它们相等),m 是每个个体每代的迁移率(有时复合参数 4Ne m 或仅 Ne m 本身表示为 M )。如果没有迁移(m = 0),则 FST 在平衡状态下将等于 1(图 5.7C);随着迁移的增加,FST 将下降至 0(图 5.7A)。公式 5.14 似乎提供了一种简单的方法来估计每代在人群之间移动的有效移民人数,Ne 人们要做的就是从数据中计算 FST(或类似 FST)统计数据。然而,要使这种关系成立,必须满足大量假设,违反任何这些假设都会导致对总迁移的极度误导性推断。这些假设中最重要的——也是最有可能不真实的——是 (1) 人口确实处于迁移漂移平衡状态,以及 (2) 人口之间没有空间结构(后一个假设仅在考虑两个以上人口时才有意义)。任何时候,由于祖先多态性而不是迁移,人口共享等位基因时,第一个假设都会被违反;这些情况正是隔离模型与此相关,将在下文进一步讨论。当没有无限数量的人口彼此交换相等数量的移民时,第二个假设就被违反了。例如,在垫脚石模型中
人口结构
FST = 0.44
人口 1
人口 2
人口 1
FST = 0.44
人口 2
人口 1
人口 2
人口 1
人口 2
A A A a aa
人口 1
人口 2
A A a a aa
人口 1
图 5.7 迁移和隔离模型之间的差异。(A-C)说明了在不同人口迁移水平下的迁移模型。每个椭圆形代表一个单独的人口。(A)中的迁移率最高,(B)中的迁移率中等,(C)中的迁移率不存在(即没有迁移)。所有的分化都是迁移和有效种群规模的函数(见公式 5.14)。(D-F)说明了自种群分裂以来不同时间下的隔离模型。图中显示了两个种群中个体染色体的假设谱系关系,底部的线代表染色体采样的时间(即现在)。(D)中分裂是最近的,(E)中分裂是过去的中间时间,(F)中分裂是很久以前的时间。所有的分化都是分裂以来的时间和有效种群规模的函数(见公式 5.15)。(第 1 章)存在空间结构,因为种群与邻近种群交换了更多的移民。在这种情况下,附近的种群将具有更相似的等位基因频率,并且将存在“距离隔离”(Wright 1943;见第 9 章)。如果违反了这些假设中的任何一个或许多其他假设,包括选择没有影响(参见 Whitlock 和 McCauley 1999),则公式 5.14 不能用于准确估计迁移率。已经开发了几种方法,可以通过允许祖先共享的等位基因和种群之间的不对称迁移来放宽其中一些假设(例如,Beerli 和 Felsenstein 1999、2001;Bahlo 和 Griffiths 2000)。然而,这些模型仍然假设种群处于平衡状态,并且它们没有区分迁移和隔离作为促成种群结构的过程。隔离模型描述了一种种群分裂情景,分裂后没有进一步的迁移(图 5.7D-F)。在这种情况下,两个产生的种群将具有相似的等位基因频率,只是因为它们一开始就有相似的等位基因频率:分裂后,这两个种群应该在祖先种群中具有大约相等的所有等位基因的代表性(图 5.7A)。由于漂移(和选择)——所谓的谱系分类过程——等位基因频率将随着时间的推移而偏离,以至于在足够的时间之后,将没有共享的等位基因,并且所有染色体将仅与同一种群内的其他染色体最密切相关——也就是说,将存在相互单系(图 5.7F)。谱系分类可能需要很长时间,并且该过程的随机性意味着单个基因座在成为相互单系所需的时间上会有所不同。作为一般准则,Hudson 和 Coyne (2002) 计算出 95% 的常染色体基因座样本在 9 到 12Ne 代后不会在两个谱系之间共享任何等位基因。在隔离模型中,对种群分化贡献最大的两个参数是种群分裂以来的时间 t 及其有效种群大小 Ne,假设它们在种群之间是相等的。隔离模型中 FST 统计量的预期值为 (Wright 1931):其中,漂移对常染色体基因座等位基因频率方差的影响在 t 代中简单地叠加。在其他所有条件相同的情况下,增加分裂时间会增加发生的漂移量,从而导致 FST 值增大(图 5.7D-F)。同样,增加种群规模会降低漂移的影响,从而减少一个或所有亚种群中降低 Ne 的 FST 过程(例如种群萎缩)将增加该亚种群中漂移的影响并导致种群分化增加。同样,漂移对非常染色体基因座的影响更大,导致这些基因座的分化增加(例如,Keinan 等人,2009 年)。如果我们假设隔离模型成立,则可以使用公式 5.15 来估计联合参数 t/2Ne。但是,同样,要使这种关系成立,必须满足许多假设。主要假设是种群之间没有交换移民。由于迁移使等位基因频率同质化,任何迁移都会降低 FST,导致低估 t/2Ne。该假设还要求种群分离是瞬间发生的,所有交换都在过去 t 代立即停止。这些假设有时可能是正确的,在这些情况下,可以估计隔离模型的参数(包括每个后代种群和祖先种群的单独种群突变参数 q)(例如,Wakeley 和 Hey 1997;Wang、Wakeley 和 Hey 1997;Leman 等人 2005)。但在许多情况下,隔离和迁移模型的主要假设都会被违反,或者我们无法先验地确定哪种模型更适合数据。这就是为什么最近的研究转向包含两个过程的模型,即隔离与迁移模型。区分迁移和漂移:隔离-迁移模型 分子群体遗传学中最具挑战性的任务之一是区分种群或物种间共享多态性的原因。由于迁移和最近的分裂事件都可能导致共享多态性(图 5.7A-F),因此迁移和隔离模型都可以解释广泛的分化值。因此,最近研究的目的是找到每个过程的不同特征,并设计一个统计框架,在这个框架内可以对迁移率、分裂时间或迁移和祖先多态性对分化水平的联合影响做出有力的推断。在这里,我描述了一些区分这些过程以及将它们整合到一个模型中的尝试。几种早期方法提出了旨在区分隔离和迁移模型的测试。 Wakeley (1996a) 表明,单个基因座上序列的成对差异的方差(公式 4.14)在迁移模型下比在隔离模型下更大,即使成对差异的预期值相同。也就是说,即使两个模型之间的 FST 预期值相同,p 的方差也会不同。如果存在不对称迁移,则在接受大量移民的种群中,p 的方差将更大。方差的预期差异假设基因座内没有重组和没有选择,这是两个非常重要的限制。由于迁移增加了交换基因的两个种群的 p 值和它们的总差异(相当于上面的 dXY),因此可以构建一个测试来区分隔离和迁移。在 Wakeley (1996b) 提出的检验中,隔离模型是零假设,因为与方差较大的零模型相比,方差较小的零模型具有更大的统计能力来拒绝它。当迁移率较低或自分化以来的时间较长时,该检验似乎具有最大的效力,即模型之间的方差差异最大。随着迁移率的增加或自分裂以来的时间减少,方差会收敛到单个随机交配种群的预期方差;在高迁移率/最近分裂情景中,这种效力的降低似乎在不同方法中普遍存在(见下文)。在另一个方法中,Wakeley 和 Hey (1997) 发现,可以计算隔离模型中预期的共享多态性数量、每个种群中的排他性多态性(即私有等位基因)以及两个种群之间的固定差异。这些汇总统计数据在比较迁移模型和隔离模型时很有用,因为单个非重组基因座可以具有共享多态性或固定差异,但不能同时具有两者(它们也可以两者都没有)。基因流将增加共享多态性的数量,同时减少种群 1 种群 2 的数量。图 5.8 两个种群的隔离与迁移模型。在最基本的模型中,有六个参数需要估计:三个种群突变参数)、两个迁移参数以及种群分裂以来的时间(t)。 IM、IMa 和 IMa2 程序按中性突变率缩放所有参数,这样估计的迁移参数为 m/µ,时间参数为 tµ。(根据 Hey 和 nielsen 2004。)固定差异和排他性多态性的数量。然后可以将这四个汇总统计数据用作针对模拟值(Wang、Wakeley 和 Hey 1997)或预期值(Kliman 等人 2000)应用测试的基础。在任一测试中拒绝零模型意味着纯隔离模型可以被丢弃作为数据的可行解释,因为这些汇总统计数据中的基因座之间存在太多差异。所有这些测试都需要来自两个种群中的每一个的适度数量(>10)的相位单倍型。刚刚描述的两种方法测试了替代迁移模型人口分裂
但不估计任何人口参数。
在涉及两个种群的隔离与迁移模型中,有六个基本参数(图 5.8):两个后代种群和单个祖先种群的 q 值、分歧以来的时间以及双向迁移率(有时会合并为单个迁移参数)。 为了估计具有大量参数的模型,贝叶斯方法通常使用合并谱系的 MCMC 抽样
来得出最可能的参数值(参见第 9 章)。使用 MCMC 估计隔离-迁移模型参数的第一种方法只能使用来自单个基因座的相位序列数据(Nielsen 和 Wakeley 2001),但随后的改进允许研究多个基因座和两个以上的后代种群(在程序 IM [Hey 和 Nielsen 2004]、IMa [Hey 和 Nielsen 2007] 和 IMa2 [Hey 2010] 中实现)。使用 MCMC 抽样的分析为每个参数的值提供了后验概率的分布。虽然该分布的峰值通常被视为参数的估计值,但曲线的形状可用于衡量对估计的支持并对比替代模型。具体而言,在试图区分隔离和迁移模型时,“[迁移参数] 峰值和迁移率为零时的概率之间的差异可用于对零基因流零假设进行似然比检验”(Pinho 和 Hey 2010,第 223 页)。一个显著的结果表明需要一定量的迁移才能更好地解释数据并拒绝纯隔离模型。使用 IM 程序及其后继程序推断隔离与迁移模型中的参数提供了一种推断近期进化过程的强大方法,但这些方法并非没有问题。大多数困难来自方法所做的假设,这些假设经常会被违反并在许多情况下影响所做的推断(Becquet 和 Przeworski 2009;Strasburg 和 Rieseberg 2010)。主要假设包括所有基因座的选择性中性(即没有正向或平衡选择)、种群结构:基因内无重组、采样后代种群或祖先种群内无进一步的种群结构、基因间独立、符合所选突变模型、无从未采样种群迁移。Strasburg 和 Rieseberg (2010) 发现 IM 软件包“相对稳健”,可以缓和任何违反上述假设的情况,尽管特定的违反情况确实会导致误导性推论。最常被违反的假设之一是没有基因内重组,其结果是增加每个后代种群的 q 估计值并增加它们之间估计的分化时间。为了解决这一限制,Hey 和 Nielsen (2004) 建议仅保留采样序列的非重组部分进行分析,尽管这种方法可能会产生其他偏差。违反 IM 假设的情况也很常见,这可能导致祖先 q 的估计值过大,包括祖先群体中未说明的结构(Becquet 和 Przeworski 2009)。最后一个警告是,这些方法似乎高估了最近分裂的迁移率(例如,Naduvilezhath、Rose 和 Metzler 2011;Hey、Chung 和 Sethuraman 2015)。隔离与迁移模型的另一个用途是尝试估计迁移时间(例如,Won 和 Hey 2004)。尤其是在考虑物种间最近的分裂时,区分具有基因流动的初级物种形成模型和分化后的二次接触模型是非常有意义的。估计迁移事件的时间应该可以让研究人员知道在给定数据的情况下哪种模型更有可能。然而,模拟(Strasburg 和 Rieseberg 2011)和理论(Sousa、Grelaud 和 Hey 2011)都表明,在这个模型中无法推断出任何迁移事件的确切时间。IM 方法使用的数据中似乎没有足够的信号来自信地确定单个迁移事件发生的时间,尽管可以对比先验定义具有不同迁移率的时代的模型(Sousa、Grelaud 和 Hey 2011)。还使用了其他方法来估计隔离-迁移模型中的参数,每种方法都有自己的局限性。几种方法使用与 IM 和相关程序相同的基本方法,但只需要非常少量的个体和非常大量的定相(Wang 和 Hey 2010)或非定相基因座(Gronau 等人 2011)。使用数据摘要的类似方法允许基因座内重组,并且可以可以采用贝叶斯方法(Becquet 和 Przeworski 2007)或“近似”贝叶斯方法(见第 9 章)。一种完全不同的方法使用多群体等位基因频谱(即所有后代群体的联合位点频谱)作为输入数据,从中推断参数(Wakeley 和 Hey 1997)。使用这种数据表示的方法可以使用数百或数千个个体和数千个标记的数据,假设多态性是独立的(有关详细信息,请参阅第 9 章)。应该强调的是,虽然这些较新的基于模型的方法被用于区分漂移和迁移作为种群分化的原因,但大多数情况下它们尚未经过广泛测试。大量研究详细阐述了违反 IM 及其后续程序假设的后果(例如 Becquet 和 Przeworski 2009;Hey 2010;Strasburg 和 Rieseberg 2010),但缺乏对新方法的此类研究并不意味着它们更准确——只是它们尚未经过测试。即使使用最现实的理论模型和最先进的计算工具,也很难将祖先多态性与迁移区分开来。这种困难部分是由于每个模型中必须做出的假设仍然不切实际,部分是由于当仅使用部分可用遗传数据时,所有进化过程都会产生非常相似的模式。未来此类方法可能需要使用改进的模型和新类型(或更大量)的数据。检测种群对之间迁移的其他方法
在第 9 章中,我们将讨论一些推断迁移的其他方法和理解迁移产生的模式的新模型。但在继续本章之前,我想介绍几种方法,这些方法可以在没有明确表达单个统计数据的预期值的情况下,预测基因流存在下的变化模式。这些方法使用模拟来生成跨基因座的预期值,因此对模拟中使用的参数的准确性相对敏感。例如,考虑一种情况,我们使用简单的汇总统计数据(例如 FST)来评估两个种群之间是否发生了迁移。如果真实数据来自两个最近分裂的种群,则假设古老的种群分裂而生成的模拟数据集可能会导致错误的迁移推断。此类误差是由于观察到的统计值远低于模拟值而导致的,对此类观察的简单解释是发生了迁移。然而,在实践中,大多数误差的方向相反,这使得检测迁移变得更加困难。其原因是发散时间是根据与迁移相同的数据估算的,从而导致测试中的循环性:如果发生迁移,则考虑到实际分裂时间,我们样本之间的序列发散将低于预期。因此,没有迁移的模拟数据将与观察到的具有迁移和较早分裂的数据紧密匹配,从而导致对迁移的保守测试。尝试通过模拟解决这些问题的一种方法是尝试检测显示出种群间迁移迹象的单个基因座,即使基因组中的基因渗入很少见。在这种情况下,希望模拟能够反映大多数基因组的非迁移历史,从而更容易检测到具有迁移信号的异常基因座。如果发现异常值,则这是发生迁移的初步证据。这种推断模式可以再次使用 ,尽管两者都存在正确解释异常基因座的困难。如上所述,FST 会受到选择的强烈影响,因此经历平衡选择的基因座的值似乎比中性进化区域(或受搭便车影响的区域)低得多。这种模式可能会被误认为是已渗入的基因座。使用具有极低中性突变率的 dXY 将具有非常低的发散水平,这再次增加了它们与渗入基因座混淆的可能性。此外,FST 均对低频迁移等位基因的存在不敏感(Geneva 等人,2015 年)。这意味着仅使用这些统计数据进行分析可能无法检测到最近的基因渗入(例如,Murray 和 Hare,2006 年)。为了检测甚至罕见的基因渗入谱系,Joly、McLenachan 和 Lockhart(2009 年)建议使用来自两个种群或物种的任何一对单倍型之间的最小序列距离。定义 kij(公式 5.12),最小序列距离 dmin,mini∈X
是两个种群 X 和 Y 中所有单倍型配对之间的最小距离(图 5.9)。该方法背后的逻辑是,任何两个彼此高度相似的序列(因此代表比种群分化时间更近的祖先)只能通过基因渗入来解释。通过将观察到的 dmin
与无迁移模型下的预期值进行比较,我们可以获得基因渗入的积极证据。
当满足其假设时,该方法具有很高的功效(Joly、McLenachan 和 Lockhart 2009),但与 dXY
一样,它假设基因座之间的突变率没有变化。
已经提出了多种解决方案来解释突变率变化,特别是在使用 dXY
时出现同样的问题。解决这个问题的一种方法是明确地在模拟中包含突变率的变化,但这些突变率很少为人所知。一种不需要估计每个基因座突变率的替代方法是使用两个分类单元与一个种群 X 相比的相对节点深度 (RND) 来解释这种变化。图 5.9 用于检测迁移的其他序列统计数据。图中显示了两个交换了移民谱系的种群的代表性谱系。虚线表示与看不见的外群 (dout) 的差异。两个种群中所有序列之间的平均距离 dXY 仅在一定程度上受到迁移事件的影响。然而,两个种群中序列之间的最小距离 dmin 比无迁移情景下的预期要低得多。 (基于 Rosenzweig 等人,2016 年)
种群 Y
外群(Feder 等人,2005 年)。RND 定义为两个种群之间的 dXY
除以每个种群与外群的平均距离:
其中 dout
是种群 X 与外群 O 之间的平均距离;dYO
是种群 Y
与外群之间的平均距离(图 5.9)。低突变率反映在 X 和 Y 之间以及每个种群与外群之间的分支长度缩短。因此,只要突变率在整个树中保持不变,RND 对低突变率就具有鲁棒性。事实上,当基因流广泛存在时,该统计数据最常用于查找未渗入的区域(例如,Nachman 和 Payseur 2012;Carneiro 等人 2014),这些区域将表现为 RND 值特别高的区域。在寻找渗入基因位点时,RND 原则上可以解决突变率变化的问题,但对低频移民仍然不敏感。最近引入了两种方法,它们对最近的迁移敏感,同时仍然对突变率的变化具有鲁棒性。Geneva 等人(2015)引入了一个统计数据 Gmin,定义为(见图 5.9):由于较低的突变率预计会对基因位点的所有谱系产生同等影响,因此通过两个种群中所有序列之间的平均距离进行标准化将解释基因位点之间不同的进化率。虽然 Gmin
有能力检测低频率的移民,但当移民等位基因的频率较高时,它就会失去能力。这可能是因为
随着移民谱系的频率上升,dXY
会降低。当移民等位基因
接近固定时,dmin
的比率会向 1 移动,接近
没有移民时的预期值。
一个对低频率和高频率移民都敏感的统计数据——
同时仍然对突变率变化具有鲁棒性——结合了 dmin
和 RND 的最佳方面。Rosenzweig 等人 (2016) 将他们的统计数据
定义为(见图 5.9):
低突变率反映在缩短的外群分支长度中,
(如 RND)对可变突变率具有鲁棒性。同样,像两者一样,
对甚至罕见的移民单倍型也很敏感。该统计数据的主要优势在于,即使移民频率很高,它仍然很有效(Rosenzweig 等人,2016 年)。与上述论点类似的论点也可用于查找与单个种群中所有其他单倍型距离比预期更远的单个单倍型,因为这些单倍型可以代表最近渗入的序列(例如,Brandvain 等人,2014 年)。
除了刚刚描述的“最小距离”方法外,我们还可以考虑最近渗入对种群结构连锁不平衡模式留下的不同信号。Machado 等人(2002 年)指出,在隔离和迁移模型下,共享多态性之间的 LD 模式预计会有所不同(图 5.10)。在隔离模型中,共享多态性被认为存在于祖先群体中,因此被认为经历了多轮重组,并且预计彼此之间不会存在强烈的 LD,也不会在每个后代群体中都具有排他性的多态性。相反,在迁徙中n 模型中,共享多态性被认为是从一个种群向另一个种群渗入的结果,因此预计它们彼此之间存在强烈的 LD,至少在接收移民的种群中是如此。此外,该模型还提供了有关 LD 符号的具体预测:随着迁移,两个渗入在一起的共享多态性的派生等位基因将呈正相关,而一个共享多态性和一个排他性多态性的派生等位基因将呈负相关(图 5.10)。在隔离模型下,LD 符号没有特定的方向性。 Machado 及其同事 (2002) 提出了一种统计方法,该方法取两个平均 LD 测量值之间的差异——第一个是所有共享多态性对之间的差异,第二个是所有一个是共享多态性而另一个是排他多态性的位点对之间的差异——并使用隔离模型下推断的种群历史的模拟生成 P 值。与此处描述的许多其他方法一样,当迁移是近期发生时,该方法最有能力检测出与隔离模型的显著偏差 祖先种群 1 P 图 5.10 迁移对重组位点内连锁不平衡模式的影响。每行字母代表一个单倍型,祖先种群在所有四个位点上都是单态的。分离后,种群 1 发生 A→a 和 B→b 突变,种群 2 发生 C→c 和 D→d 突变。
迁移事件将单倍型 ABcd 引入种群 1。
根据祖先和派生状态定义 lD 的符号,这种基因渗入的结果是种群 1 中具有共享多态性的位点(C/c 和 D/d)之间的 lD 为正,而这些共享多态性与种群 1 独有的多态性(A/a 和 B/b)之间的 lD 为负。 (根据
Machado 等人,2002 年)
种群 2
(因为基因渗入区域的 LD 尚未分解)和
当种群分裂更早的时候(因为在分裂之前实际上一直存在的共享多态性之间的“背景”LD 会更少)。该测试的结果也完全取决于模拟的特定隔离场景,因此使用不切实际的参数进行模拟可能会导致拒绝零模型,即使没有迁移。
尽管 Machado 等人(2002) 研究了多个种群中采样的单个基因座中包含的 LD 模式,类似的想法已用于仅使用来自单个种群的 LD 数据检测古代基因渗入(Wall 2000b;Plagnol 和 Wall 2006)以及使用全基因组数据集检测密切相关种群之间的所谓迁移区(或混合块)(例如,Falush、Stephens 和 Pritchard 2003)。此类区域的长度可用于估计推断的迁移事件或迁移率变化的时间(例如,Koopman 等人 2007;Pool 和 Nielsen 2009;Moorjani 等人 2011),或作为种群间迁移和隔离模型的明确测试(Loh 等人 2013)。 LD 模式和由于多个种群之间迁移而产生的每个基因组的比例在首先定义种群以及在分配每个个体在种群中的成员资格方面非常有用。在下一节中,我将讨论这些基本问题并提出解决方案。
定义种群
识别种群及其中的个体
到目前为止讨论的所有分析都假设我们对我们感兴趣的物种的种群结构有所了解。具体来说,我们假设我们知道有多少个种群,并且可以将样本分配给这些种群。如果不这样做,我们就无法测量种群之间等位基因频率的差异,也无法询问是否有证据表明存在显著的种群结构、迁移等。这些问题都要求我们首先识别种群并将我们的样本分配给这些种群。然而,在许多情况下,这些分配可能事先并不知道,或者可能仅根据样本采集的地理位置推断出来。此外,可能存在隐秘的种群结构,掩盖了从同一地点采集的样本实际上属于不同种群的事实。在这两种情况下,我们都可以使用统计工具来帮助我们对物种内亚种群的组成进行概率推断。必须对提前知道种群的情况和不知道种群的情况进行重要区分。在前者中,要解决的问题是将个体分配到种群中——因此使用的方法称为分配测试。所有这些方法(例如,Paetkau 等人,1995 年;Rannala and Mountain 1997;
Cornuet 等人 1999)要求分配个体的多位点基因型,以及每个可能的源种群的种群等位基因频率;他们还假设每个基因座的 HWE 和基因座之间的连锁平衡。然后,将个体最佳地分配到源种群是基于个体的基因型与每个种群中的等位基因频率之间的匹配,并且可能伴随着分配中的不确定性测量。分配的准确性在很大程度上取决于种群间等位基因频率差异的大小、种群等位基因频率估计的准确性以及正确源种群的纳入(Cornuet 等人 1999)。
尤其是当源种群等位基因频率的估计是基于少数个体时,考虑到小样本量,在分配中具有一定的不确定性度量非常重要。由于基因型和种群等位基因频率不匹配,种群也可能被排除在个体的可能来源之外。如果正确的源种群无意中被排除在研究之外,则所有抽样种群的高排除概率(或低分配概率)可能表明其缺失。在未预先定义种群的情况下,我们必须使用替代工具同时将个体分配到种群中,并估计种群数量及其在每个基因座的等位基因频率。此外,我们样本中的一些个体可能有混合血统——也就是说,他们可能有来自多个种群的遗传贡献。我们将这样的个体称为混合个体。我们希望识别这些个体,并估计每个源种群对其血统的贡献比例。
幸运的是,有多种方法可以执行所有这些计算,甚至更多。尽管每种方法在细节上有所不同,但许多方法都使用相同的基本原理:即最小化哈代-温伯格不平衡和连锁不平衡。下面我将描述程序结构(Pritchard、Stephens 和 Donnelly 2000)使用的基本方法,这是在不知道种群数量或每个个体在这些种群中的成员身份的情况下推断种群结构存在的最广泛使用的方法。
使用 Wahlund 效应识别种群结构
我们已经看到了 Wahlund 效应如何解释哈代-温伯格不平衡的情况,即当来自多个亚种群的个体被错误地认为来自同一种群时。按照类似的逻辑,将个体错误地分配到亚种群也会导致它们通过引入不太可能的基因型而处于哈代-温伯格不平衡状态。
因此,找到个体与种群的最佳分配(或找到最可能的种群数量)的一种方法是尝试最小化哈代-温伯格不平衡量。大多数软件包通过尝试大量不同的个体与种群分配来实现这一点,通常使用 MCMC 方法。最佳分配是导致每个种群中哈代-温伯格不平衡量最少的配置。因此,这些方法都假设每个种群中都存在哈代-温伯格平衡,唯一的例外是允许近亲繁殖的情况(例如,Gao、Williamson 和 Bustamante 2007)。还有第二种由个体与种群错误分配产生的不平衡:连锁不平衡。要了解为什么会这样,请考虑两个在两个基因座上固定了替代等位基因的种群(图 5.11)。种群 1 只有 AB 个个体,而种群 2 只有 ab 个个体。在每个种群中都没有 LD,但被视为单个种群时,两组等位基因之间存在完美关联(即完美 LD)。Wahlund(1928)实际上是第一个指出这个问题的人,但后来被多个其他团体重新发现(Cavalli-Sforza 和 Bodmer 1971;Sinnock 和 Sing 1972;Nei 和 Li 1973;Prout 1973)。这种效应有时被称为多位点 Wahlund 效应(Feldman 和 Christiansen 1974)或混合 LD(Falush、Stephens 和 Pritchard 2003)。种群之间固定的差异并非产生这种效应的必要条件:如果个体被错误地归类到种群中,任何等位基因频率的差异都可能产生 LD。事实上,产生的不平衡程度与种群之间等位基因频率的差异成正比。考虑两个基因座,每个基因座都有两个等位基因:A/a 和 B/b。如果我们将种群 1 中 A 等位基因的频率表示为 p1A,将种群 2 中 B 等位基因的频率表示为 p1B,将种群 2 中 B 等位基因的频率表示为 ,那么LD 量由以下公式给出:
D y y p p p p
其中 y 表示来自种群 1 的个体占总样本的比例,1-y 表示来自种群 2 的比例。可以很容易地看出,这种抽样形式即使在不同染色体上的基因座之间也会产生连锁不平衡。与单基因座不平衡一样,个体到种群的最佳分配将是
图 5.11 通过对多个种群进行抽样来产生连锁不平衡。两个种群(黄色椭圆内)被视为单个种群(白色椭圆)。种群 1 固定为 AB 单倍型,而种群 2 固定为 ab 单倍型。这两个基因座在种群 1 和 2 中都处于连锁平衡状态,但当将其视为单个种群时,它们之间存在完美的连锁不平衡。
种群 1
种群 2
种群结构
最小化位点之间的连锁不平衡。实际上,最小化这两种不平衡在计算上都很有挑战性,尤其是当人们还试图找到最可能的种群数量以及每个种群对每个个体祖先的可能贡献时。但诸如structure之类的软件包可以完成这些任务,以及识别单个基因座的祖先。
从种群结构的确定中进行进化推断
这里描述的方法的最重要用途之一是找到样本中包含的“最佳”种群数量。由于 Hardy-Weinberg 不平衡和连锁不平衡都会随着种群数量(表示为 K)的增加而进一步最小化,因此数据的可能性也会随着 K 的增大而增大。与许多统计问题一样,我们希望避免过度拟合具有大量参数的模型,而是选择足以解释数据的最小参数数量(参见 Burnham 和 Anderson 2002)。虽然有许多不同的方法可以推断 K 的最佳值(如下所述),但也应该记住,种群可以是主观实体,并且种群的确切划分可能会根据所提出的问题而改变(Waples 和 Gaggiotti 2006)。事实上,当人口结构是分层结构时,数据集的全局“最佳”K 可能对某些问题有用,而对个别人口的进一步细分可能对其他问题有用(例如,Rosenberg 等人,2002 年)。
对于几乎完全由混合个体组成的人口(例如,非裔美国人),甚至不清楚 K 的值应该代表什么:源人口的数量还是当前的单一人口?
在一个类似的模拟示例中,Pritchard、Stephens 和 Donnelly(2000 年)推断单个混合种群的 K = 2。作为选择单个最佳 K 值的替代方案,还可以对多个 K 值进行下游分析,并报告每个值的结果。图 5.12 显示了 Rosenberg 等人(2002 年)分析的全球人类样本增加 K 的结果。有两种主要方法可以推断最佳种群数量。第一种方法是使用结构等程序的输出对每个 K 值下数据集的可能性进行事后分析(有关此方法的注意事项,请参阅 Janes 等人 2017 年)。由于结构会计算固定 K 值下个体的最佳分配,因此必须使用 K = 1、2、3 . . . n 进行独立运行,直到达到某个最大种群数量 n。然后可以根据数据可能性随 K 增加而增加的速率(Evanno、Regnaut 和 Goudet 2005)或更严格的统计模型选择方法(例如 Gao、Bryc 和 Bustamante 2011)推断出 K 的最佳值。在第二种方法中,种群数量是在分配过程中同时估计的。软件可以
为单次运行中考虑的种群数量指定上限,使用 MCMC 过程拆分或合并这些种群
(例如,Corander、Waldmann 和 Sillanpaa 2003;Corander 等人 2004),或者它
班图(肯尼亚)
姆布提俾格米人
巴科拉俾格米人
推断种群数量和身份的一个重要问题是抽样的影响。与具有预定义种群的分配测试一样,种群识别的准确性取决于所包括的个体数量、使用的基因座数量以及种群之间的等位基因频率差异(Pritchard、Stephens 和 Donnelly 2000;Rosenberg 等人 2005)。此外,种群识别可能受到个体内混合量和数据集中混合个体的比例(Pritchard、Stephens 和 Donnelly 2000)以及从每个“纯”种群中抽取的个体数量(Fogelqvist 等人 2010)的强烈影响。甚至对于一个低样本的有限范围
在另一种方法中,主成分分析 (PCA) 可用于查找样本中的隐藏结构(参见第 9 章)。虽然 PCA 方法与迄今为止描述的混合模型确实存在潜在关系(Engelhardt 和 Stephens 2010;Lawson 等人 2012),但它们不会将个体分配到种群中。然而,Patterson、Price 和 Reich (2006) 表明,PCA 研究中的重要特征值的数量等于 K − 1。因此,PCA 可用于独立(并且更快速地)计算数据集中的最佳种群数量。可以将 K 视为给定某些先验分布的随机变量(Dawson 和 Belkhir 2001;Huelsenbeck 和 Andolfatto 2007)。一些方法还可以使用个体的空间采样位置来提供种群数量和个体分配到种群的先验信息(Guillot 等人,2005 年;François、Ancelet 和 Guillot,2006 年;Hubisz 等人,2009 年)。
图 5.12 人类种群结构。每个个体都用一条细垂直线表示,该线代表 K 个种群中每个种群的混合比例。黑线将不同预定义种群(在底部命名)中的个体分开,上面给出了种群的大陆位置。每行有 K 种颜色用于区分每个个体的混合比例。
(摘自 Rosenberg 等人,2002 年)
巴勒斯坦
汉族(中国北方)
美拉尼西亚
中东
中东
中东
中亚/南亚
中亚/南亚
中亚/南亚
中亚/南亚
中亚/南亚
中亚/南亚
中亚/南亚
中亚/南亚
人口结构
值,即使没有结构,也可能识别出重要的结构(Orozco-terWengel、Corander 和 Schlötterer,2011 年)。
一旦做出了最佳的种群选择并将个体分配到种群中,进一步的分析就可以识别出移民或混合个体。最近的移民将具有统计上显着的分配到源种群,这些分配与其采样位置重叠的种群不匹配(Rannala 和 Mountain,1997 年)。大多数此类方法只能识别移民或估计最近几代的移民率(例如 Wilson 和 Rannala 2003),因为重复的回交会抹去原始源种群的遗传信号。然而,许多被确定为最近移民的个体可能被错误标记或被污染的样本(Rosenberg 等人 2002)。结构报告的混合比例——以及类似方法,如 FRAPPE(Tang 等人 2005)和 ADMIXTURE(Alexander、Novembre 和 Lange 2009)——揭示了单个样本的祖先。识别混合个体对许多应用都很重要,可以作为关联研究中人口分层混杂效应的校正(例如,Hoggart 等人,2003 年;Price 等人,2006 年),帮助确定濒危种群的状况(例如,Beaumont 等人,2001 年),并为混合区研究提供关键信息(例如,Nielsen 等人,2003 年)。它不仅可以估计每个个体的单个基因组范围的混合比例,还可以估计单个基因座的祖先(分别称为全球和本地祖先;Alexander、Novembre 和 Lange,2009 年)。任何个体的基因组都可以被分成单独的染色体“块”或单倍型,每个块都有自己的祖先起源、物理长度和种群频率。尽管结构的原始版本需要不相连的标记,因此“混合”LD 是唯一的不平衡来源(见上文),但较新的版本可以考虑由连锁标记块的渗入(混合 LD)产生的 LD 以及 LD 的背景水平(Falush、Stephens 和 Pritchard 2003;另见 Patterson 等人 2004;Tang 等人 2006;Sankararaman 等人 2008)。如本章前面所述,识别这些混合块可用于推断迁移过程的特征(例如,Koopman 等人,2007 年;Pool 和 Nielsen,2009 年;Loh 等人,2013 年),以及校正关联研究中的分层(例如,Hoggart 等人,2004 年),甚至推断重组率(Wegmann 等人,2011 年)。进一步使用单倍型特异性祖先,使用 fineSTRUCTURE 程序中实现的方法(Lawson 等人,2012 年),可以揭示使用未链接标记无法显示的精细尺度种群结构。最后,必须对种群结构和混合的推断提出一个非常重要的警告。尽管在结构和 ADMIXTURE 等程序中,祖先分配被称为混合比例(我在这里也使用过这个术语),但它们实际上并没有表明是否发生了混合,因此可能具有误导性gly 命名。考虑这样一种情况,即有一个包含大量祖先多态性的单一大型种群,再加上几个较小的种群,这些种群已经从较大的种群中分离出来,并且每个种群都经历了瓶颈。在许多情况下,较小的种群将被软件识别为单独的种群,而单个较大的种群则表示为来自所有其他种群的祖先的混合。在这种情况下,混合比例不应被视为任何混合历史的证据;相反,它们应该被理解为仅仅表明与许多较小种群共享祖先的分配。因此,结构图(和类似的图)本身不能用于推断混合的历史(有关更多讨论,请参阅第 9 章)。聚结 6
模拟 DNA 序列样本
为了准确推断影响分子变异的进化力量,我们必须能够准确模拟 DNA 序列。理想情况下,我们希望能够在各种模型、不同的人口历史、选择形式和强度以及任何其他感兴趣的参数下模拟种群。
此类模拟的结果应该是 DNA 序列样本,相当于我们从自然种群中收集的样本。
这个过程重复了数千次,然后可以用来找到最适合我们观察到的数据的模型,或者作为零分布,我们可以用它来测试特定的假设。
我们如何模拟这样的种群?最直接的方法是,从大量二倍体个体(相当于我们想要模拟的种群规模)开始,这些个体根据我们选择的种群模型进化。我们将对适当长度的序列(可能等于我们希望与模拟进行比较的 DNA 序列的长度)应用突变和重组,同时进行交配和任何可能的自然选择。然后,该系统必须运行多代,至少直到种群达到平衡,最后需要从种群中抽取少量染色体以创建一个模拟数据集。为了生成数千个独立模拟的样本,这个过程必须运行数千次。这个过程通常被称为正向模拟,因为它从最初相同的种群开始向前进行。从上面的描述中可以明显看出,这种方法非常低效:我们只想知道样本的属性,但我们正在跟踪整个种群。为了解决这种低效率问题,几位数学遗传学家独立提出了后来被称为合并过程的方法(Kingman 1982a、1982b、1982c;Hudson 1983a;Tajima 1983)。合并过程的核心是,我们可以根据生成谱系间关系集(系谱)的简单规则来生成 DNA 序列样本。这些规则使我们能够生成具有几乎任何人口历史的样本,而无需模拟整个种群。由于该过程从现在开始并向后运行,因此被称为向后模拟。如今,有许多软件包可用于执行合并模拟(表 6.1)。由于合并过程仅考虑样本而不是整个种群,因此它可以成为生成大量模拟数据集的一种非常有效的方法,但它也存在自身的局限性,无论是生物学还是计算上的。从生物学上讲,合并是模型的模型:也就是说,它是 Wright-Fisher 或 Moran 种群(尽管非常好)的近似值,而 Wright-Fisher 或 Moran 种群本身是自然种群的近似值。合并的一个关键假设是样本大小 n 比有效种群大小 Ne 小得多。违反这一假设可能会导致对种群过程的误导性推断(例如,Wakeley 和 Takahashi
■ 表 6.1 用于模拟 DNA 序列种群样本的程序
程序来源
COALESCENT(“后向”)模拟软件
ms Hudson 1990;Hudson 2002
GENOME Liang 等人 2007
SIMCOAL/SIMCOAL 2.0 Excoffier 等人 2000;Laval 和 Excoffier 2004
CoaSim Mailund 等人 2005
Recodon Arenas 和 Posada 2007
discoal Kern 和 Schrider 2016
msprime Kelleher 等人 2016
WRIGHT-FISHER(“前向”)模拟软件:
EASYPOP 巴卢克斯 2001
simuPop 彭和金梅尔 2005
尼莫纪尧姆和鲁日蒙 2006
弗雷杰尼·霍加特等人。 2007年;查多-海姆等人。 2008年
ForSim 兰伯特等人。 2008年
FORWSIM Padhukasahasram 等人。 2008年
GENOMEPOP 卡瓦哈尔-罗德里格斯 2008
SFS_CODE 埃尔南德斯 2008
FFPOPSim 扎尼尼和内尔 2012
fwdpp 桑顿 2014
SLiM/SLiM 2 梅塞尔 2013;Haller 和 Messer 2017
ARGON Palamara 2016
近似合并(“侧向”)模拟软件
FastCoal McVean 和 Cardin 2005;Marjoram 和 Wall
MaCS Chen 等人 2009
fastsimcoal/fastsimcoal2(Excoffier 和 Foll 2011;Excoffier 等人 2013)
合并
2003)。虽然可以修改标准合并以更精确地匹配 Wright-Fisher 模型并放宽 n << Ne 假设,但这种修改会导致算法速度下降(Fu 2006)。更重要的是,从生物学角度来看,合并只会在没有自然选择的种群中生成一小部分随机染色体样本。
它不是对整个种群的模拟,因此无法提供除样本属性之外的任何结果。尽管模拟具有选择的合并方法一直在改进(例如,Spencer 和 Coop 2004;Teshima 和 Innan 2009;Ewing 和 Hermisson 2010;Kern 和 Schrider 2016),但可以建模的选择形式仍然有限。从计算角度来看,当计算机处理器速度和内存资源有限时,合并提供的优势更为重要,而这已越来越不成问题。技术发展使得合并的效率变得不那么重要,除非在使用贝叶斯抽样方法的应用中(参见第 9 章)。然而,最重要的是,当模拟基因组的非常大的区域或具有非常高重组率的区域时,合并可能变得非常低效,以至于无法使用它来建模当前正在收集的数据集。解决此问题的一种方法是发明近似合并方法,该方法基于在沿着一段 DNA 移动时生成相关谱系,而不是为整个区域生成一个大谱系(Wiuf 和 Hein 1999);因此它们是横向模拟。这些方法更正式地称为顺序马尔可夫合并 (SMC) 模型(McVean 和 Cardin 2005;Marjoram 和 Wall 2006),并且有多个程序可以执行它们(表 6.1)。
SMC 模型已经变得非常有用,但它们与自然种群的距离甚至更大:它们是模型的模型的模型!
将来,正向模拟可能会成为此类方法中最广泛使用的方法。越来越多的快速灵活的正向模拟器可以在许多不同的自然选择形式和许多不同的人口历史下对非常大的基因组区域进行建模(表 6.1)。计算技术的进步使这些方法更加可行,而 DNA 测序技术的进步可能使它们成为必需。虽然到目前为止,我只介绍了合并算法作为生成样本的算法,但这种方法有许多重要用途(请参阅 Hein、Schierup 和 Wiuf 2005 和 Wakeley 2009 以获得良好的概述)。合并算法为我们提供了一种概率建模谱系的方法,因此为分子群体遗传学中的各种结果提供了预期。这些预期中的许多都用在了本书的后面章节中。联合体还为我们提供了一个从谱系角度思考的框架,因此可以让我们深入了解我们采样的 DNA 序列之间的潜在关系。这个框架对于直观地了解群体遗传过程非常有帮助,因此在本章的其余部分,我将讨论中性联合体谱系的基础知识,并解释联合体的一些最重要的方面。在后面的章节中,我们将研究自然选择和非平衡人口历史对某个基因座谱系的影响。
一本关于分子群体遗传学的书,内容包括但不限于:Tajima's D,不完全谱系分选,ABBA-AABB等等莫名其妙的考点。