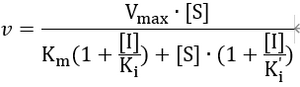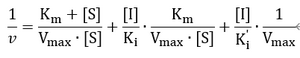酶动力学作图:修订间差异
无编辑摘要 |
无编辑摘要 |
||
| 第1行: | 第1行: | ||
== 酶动力学 == | == 酶动力学 == | ||
=== Michaelis- | === Michaelis-Menten方程一般推导及意义解读 === | ||
假设理想酶促反应'''E+S⇌ES→E+P'''正向第一步反应的反应速率常数为k<sub>1</sub>, 逆向反应速率常数为k<sub>-1</sub> ,第二步反应速率常数为k<sub>2</sub>. 通常情况下,有k<sub>2</sub><<k<sub>1</sub>, 从而可得该反应的化学平衡常数K<sub>m</sub>=k<sub>-1</sub>/k<sub>1</sub>=[E][S]/[ES] ① | 假设理想酶促反应'''E+S⇌ES→E+P'''正向第一步反应的反应速率常数为k<sub>1</sub>, 逆向反应速率常数为k<sub>-1</sub> ,第二步反应速率常数为k<sub>2</sub>. 通常情况下,有k<sub>2</sub><<k<sub>1</sub>, 从而可得该反应的化学平衡常数K<sub>m</sub>=k<sub>-1</sub>/k<sub>1</sub>=[E][S]/[ES] ① | ||
| 第26行: | 第26行: | ||
注意到V<sub>max</sub>=k<sub>2</sub>[ES]<sub>max</sub>=k<sub>2</sub>[E<sub>t</sub>] | 注意到V<sub>max</sub>=k<sub>2</sub>[ES]<sub>max</sub>=k<sub>2</sub>[E<sub>t</sub>] | ||
所以, | |||
( | '''υ=V<sub>max</sub>[S]/(K<sub>m</sub>+[S]).''' | ||
上式被称为'''米氏方程''' | |||
=== 抑制剂作用的图像 === | |||
在米氏酶中,记k<sub>cat</sub>=k<sub>2</sub> | |||
那么不难得出V<sub>max</sub>=k<sub>cat</sub>[E<sub>t</sub>] | |||
即k<sub>cat</sub>的物理学意义是每单位浓度的酶总量下酶促反应的最大速率,单位是s<sup>-1</sup> | |||
可以将k<sub>cat</sub>理解成单个酶分子在一秒内转化底物的数量,或者单个酶分子转换一个底物分子所需的时间 | |||
因此,称k<sub>cat</sub>为转化数. | |||
令[S]=K<sub>m</sub>(米氏常数), 不难得出, 此时υ=V<sub>max</sub>/2, 可知K<sub>m</sub>越大,酶促反应越难达到其最大速率的一半,也就是说,K<sub>m</sub>衡量了酶与底物的亲和力,且K<sub>m</sub>与亲和力负相关。 | |||
从而,我们可以通过计算k<sub>cat</sub>/K<sub>m</sub>来衡量一个酶的“完美”程度。 | |||
已知“完美”程度较高的一种酶为磷酸丙糖异构酶TIM | |||
=== 抑制剂存在情况下的米氏方程推导 === | |||
(待续) | |||
== 动力学作图 == | |||
=== -双倒数作图 === | |||
==== 抑制剂作用的图像 ==== | |||
竞争:交点在纵轴(因为Vmax没变,纵截距没变) | 竞争:交点在纵轴(因为Vmax没变,纵截距没变) | ||
| 第43行: | 第69行: | ||
非+反混合型:交点在第三象限 | 非+反混合型:交点在第三象限 | ||
=== 多底物的图像 === | ==== 多底物的图像 ==== | ||
乒乓机制:以1/底物A浓度为横轴,1/V为纵轴,不同B浓度做出的直线: | 乒乓机制:以1/底物A浓度为横轴,1/V为纵轴,不同B浓度做出的直线: | ||
| 第49行: | 第75行: | ||
* 序列机制:交于第二象限 | * 序列机制:交于第二象限 | ||
=== -双倒数作图 === | |||
=== 双倒数作图 === | |||
1/V-1/S,纵截距:1/Vmax;横截距:-1/Km | 1/V-1/S,纵截距:1/Vmax;横截距:-1/Km | ||
=== Eadie- | === -Eadie-Hofstee作图 === | ||
V-V/S。纵截距:Vmax,斜率:-Km | V-V/S。纵截距:Vmax,斜率:-Km | ||
=== Hanes-Woolf作图 === | === -Hanes-Woolf作图 === | ||
S/V-S,横截距:-Km,斜率:1/Vmax | S/V-S,横截距:-Km,斜率:1/Vmax | ||
=== Eisenthal&Cornish-Bowden作图 === | === -Eisenthal&Cornish-Bowden作图 === | ||
在横轴上找到某浓度对应点,在纵轴上找到该浓度下速度对应点,连出一条直线;多组数据直线应当通过一点,此点坐标即是(Km , Vmax)。 | 在横轴上找到某浓度对应点,在纵轴上找到该浓度下速度对应点,连出一条直线;多组数据直线应当通过一点,此点坐标即是(Km , Vmax)。 | ||
| 第67行: | 第91行: | ||
** 如果有多条线,那么交点坐标是(Km,Vmax) | ** 如果有多条线,那么交点坐标是(Km,Vmax) | ||
== Dixon作图 == | === -Dixon作图 === | ||
Dixon作图可以用于求得抑制剂的抑制常数Ki。 | Dixon作图可以用于求得抑制剂的抑制常数Ki。 | ||
2025年2月15日 (六) 18:51的版本
酶动力学
Michaelis-Menten方程一般推导及意义解读
假设理想酶促反应E+S⇌ES→E+P正向第一步反应的反应速率常数为k1, 逆向反应速率常数为k-1 ,第二步反应速率常数为k2. 通常情况下,有k2<<k1, 从而可得该反应的化学平衡常数Km=k-1/k1=[E][S]/[ES] ①
同时,做出如下假设:
1.底物过量,即[S]>>[E]
2.k-2→0,且第二步反应是决速步骤(因其不可逆)
3.体系达到稳态
酶的总浓度[Et]是不变的,[Et]=[E]+[ES] ②
与①式联立,变形可得[Et]=[E](1+[S]/Km)
[E]=[Et]/(1+[S]/Km) ③
由假设2,υ=k2[ES]=k2[E][S]/Km
再与③式联立解得
υ=k2[Et][S]/(Km+[S])
注意到Vmax=k2[ES]max=k2[Et]
所以,
υ=Vmax[S]/(Km+[S]).
上式被称为米氏方程
在米氏酶中,记kcat=k2
那么不难得出Vmax=kcat[Et]
即kcat的物理学意义是每单位浓度的酶总量下酶促反应的最大速率,单位是s-1
可以将kcat理解成单个酶分子在一秒内转化底物的数量,或者单个酶分子转换一个底物分子所需的时间
因此,称kcat为转化数.
令[S]=Km(米氏常数), 不难得出, 此时υ=Vmax/2, 可知Km越大,酶促反应越难达到其最大速率的一半,也就是说,Km衡量了酶与底物的亲和力,且Km与亲和力负相关。
从而,我们可以通过计算kcat/Km来衡量一个酶的“完美”程度。
已知“完美”程度较高的一种酶为磷酸丙糖异构酶TIM
抑制剂存在情况下的米氏方程推导
(待续)
动力学作图
-双倒数作图
抑制剂作用的图像
竞争:交点在纵轴(因为Vmax没变,纵截距没变)
非竞争:交点在横轴(Km没变,横截距没变)
反竞争:相互平行,没有交点(Km,Vmax同时除以1+I/Ki,比值(斜率)没变)
混合型(非+竞争混合型):交点在第二象限
非+反混合型:交点在第三象限
多底物的图像
乒乓机制:以1/底物A浓度为横轴,1/V为纵轴,不同B浓度做出的直线:
- 乒乓机制:直线之间平行
- 序列机制:交于第二象限
-双倒数作图
1/V-1/S,纵截距:1/Vmax;横截距:-1/Km
-Eadie-Hofstee作图
V-V/S。纵截距:Vmax,斜率:-Km
-Hanes-Woolf作图
S/V-S,横截距:-Km,斜率:1/Vmax
-Eisenthal&Cornish-Bowden作图
在横轴上找到某浓度对应点,在纵轴上找到该浓度下速度对应点,连出一条直线;多组数据直线应当通过一点,此点坐标即是(Km , Vmax)。
- 总结:考题可能会给你一个图,只标注了横坐标和纵坐标的含义。
- 如果只有一条线且不是常见的双倒数作图,根据横纵轴量纲判断截距的含义:若纵轴是速度,纵截距就是Vmax,斜率相应的是Km;若横轴是浓度,横截距就是Km,斜率相应的代表Vm;注意量纲和正负是否合适。
- 如果有多条线,那么交点坐标是(Km,Vmax)
-Dixon作图
Dixon作图可以用于求得抑制剂的抑制常数Ki。
具体过程如下:
针对较为通常的含抑制剂的米氏方程:
其可以被转换为:
因此其表现为[S]一定时,1/v关于[I]的线性函数。
当[S]不同时,联立方程可解[I]=-Ki。
Dixon作图以抑制剂浓度I为横轴,1/V为纵轴。
对于非竞争抑制剂,Ki=Ki',故不同底物浓度的直线交于一点(-Ki,0)。
对于竞争性抑制剂,消去(2)右侧最后一项,可解得交于同一点(-Ki,1/Vmax)。
对于反竞争抑制剂,消去(2)右侧第二项,可解得直线间相互平行,不可计算。